Doctoral Thesis
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Crystallography News British Crystallographic Association
Crystallography News British Crystallographic Association Issue No. 100 March 2007 ISSN 1467-2790 BCA Spring Meeting 2007 - Canterbury p8-17 Patrick Tollin (1938 - 2006) p7 The Z’ > 1 Phenomenon p18-19 History p21-23 Meetings of Interest p32 March 2007 Crystallography News Contents 2 . From the President 3 . Council Members 4 . BCA Letters to the Editor 5 Administrative Office, . Elaine Fulton, From the Editor 6 Northern Networking Events Ltd. 7 1 Tennant Avenue, Puzzle Corner College Milton South, . East Kilbride, Glasgow G74 5NA Scotland, UK Patrick Tollin (1938 - 2006) 8-17 Tel: + 44 1355 244966 Fax: + 44 1355 249959 . e-mail: [email protected] BCA 2007 Spring Meeting 16-17 . CRYSTALLOGRAPHY NEWS is published quarterly (March, June, BCA 2007 Meeting Timetable 18-19 September and December) by the British Crystallographic Association, . and printed by William Anderson and Sons Ltd, Glasgow. Text should The Z’ > 1 Phenomenon 20 preferably be sent electronically as MSword documents (any version - . .doc, .rtf or .txt files) or else on a PC disk. Diagrams and figures are most IUCr Computing Commission 21-23 welcome, but please send them separately from text as .jpg, .gif, .tif, or .bmp files. Items may include technical articles, news about people (e.g. History . 24-27 awards, honours, retirements etc.), reports on past meetings of interest to crystallographers, notices of future meetings, historical reminiscences, Groups .......................................................... 28-31 letters to the editor, book, hardware or software reviews. Please ensure that items for inclusion in the June 2007 issue are sent to the Editor to arrive Meetings . 32 before 25th April 2007. -

Ccp4 Newsletter on Protein Crystallography
CCP4 NEWSLETTER ON PROTEIN CRYSTALLOGRAPHY An informal Newsletter associated with the BBSRC Collaborative Computational Project No. 4 on Protein Crystallography. Number 41 Fall 2002 Contents CCP4 News 1. News from CCP4. Alun Ashton, Charles Ballard, Peter Briggs, Maeri Howard-Eales, Pryank Patel and Martyn Winn. 2. Developments with CCP4i: October 2002. Peter Briggs. 3. Developments with the CCP4 library II. Martyn Winn, Charles Ballard and Eugene Krissinel. General News 4. BioMed College at Daresbury. Gareth Jones. Software 5. Handling reflection data using the Clipper libraries. Kevin Cowtan, Department of Chemistry, University of York, UK. Theory and Techniques 6. Atomic displacement in incomplete models caused by optimisation of crystallographic criteria. P.V Afonine, Université Henri Poincaré, Nancy, France, Centre Charles Hermite, LORIA, Villers-lès-Nancy, France. 7. Modelling of bond electron density by Gaussian scatters at subatomic resolution. P. Afonine(1,2), V. Pichon-Pesme(1), N. Muzet(1), C. Jelsh(1), C Lecomte(1) and A. Urzhumtsev(1), (1) Université Henri Poincaré, Nancy, France, (2) Centre Charles Hermite, LORIA, Villers-lès-Nancy, France. 8. Bulk-solvent correction for use with the CCP4 version of AMoRe. Guido Capitani(1) and Andrei Fokine(2), (1) University of Zürich, Switzerland, (2) Université Henry Poincaré, Nancy, France. 9. Variation of solvent density and low-resolution ab initio phasing. Andrei Fokine, Université Henry Poincaré, Nancy, France. 10. Retrieval of lost reflections in high resolution Fourier syntheses by 'soft' solvent flattening. Natalia L. Lunina(1), Vladimir Y. Lunin(1) and Alberto D. Podjarny(2), (1) Russian Academy of Sciences, Russia, (2) CU Strasbourg, France. Bulletin Board 11. -

TRINITY COLLEGE Cambridge Trinity College Cambridge College Trinity Annual Record Annual
2016 TRINITY COLLEGE cambridge trinity college cambridge annual record annual record 2016 Trinity College Cambridge Annual Record 2015–2016 Trinity College Cambridge CB2 1TQ Telephone: 01223 338400 e-mail: [email protected] website: www.trin.cam.ac.uk Contents 5 Editorial 11 Commemoration 12 Chapel Address 15 The Health of the College 18 The Master’s Response on Behalf of the College 25 Alumni Relations & Development 26 Alumni Relations and Associations 37 Dining Privileges 38 Annual Gatherings 39 Alumni Achievements CONTENTS 44 Donations to the College Library 47 College Activities 48 First & Third Trinity Boat Club 53 Field Clubs 71 Students’ Union and Societies 80 College Choir 83 Features 84 Hermes 86 Inside a Pirate’s Cookbook 93 “… Through a Glass Darkly…” 102 Robert Smith, John Harrison, and a College Clock 109 ‘We need to talk about Erskine’ 117 My time as advisor to the BBC’s War and Peace TRINITY ANNUAL RECORD 2016 | 3 123 Fellows, Staff, and Students 124 The Master and Fellows 139 Appointments and Distinctions 141 In Memoriam 155 A Ninetieth Birthday Speech 158 An Eightieth Birthday Speech 167 College Notes 181 The Register 182 In Memoriam 186 Addresses wanted CONTENTS TRINITY ANNUAL RECORD 2016 | 4 Editorial It is with some trepidation that I step into Boyd Hilton’s shoes and take on the editorship of this journal. He managed the transition to ‘glossy’ with flair and panache. As historian of the College and sometime holder of many of its working offices, he also brought a knowledge of its past and an understanding of its mysteries that I am unable to match. -

Pnas11052ackreviewers 5098..5136
Acknowledgment of Reviewers, 2013 The PNAS editors would like to thank all the individuals who dedicated their considerable time and expertise to the journal by serving as reviewers in 2013. Their generous contribution is deeply appreciated. A Harald Ade Takaaki Akaike Heather Allen Ariel Amir Scott Aaronson Karen Adelman Katerina Akassoglou Icarus Allen Ido Amit Stuart Aaronson Zach Adelman Arne Akbar John Allen Angelika Amon Adam Abate Pia Adelroth Erol Akcay Karen Allen Hubert Amrein Abul Abbas David Adelson Mark Akeson Lisa Allen Serge Amselem Tarek Abbas Alan Aderem Anna Akhmanova Nicola Allen Derk Amsen Jonathan Abbatt Neil Adger Shizuo Akira Paul Allen Esther Amstad Shahal Abbo Noam Adir Ramesh Akkina Philip Allen I. Jonathan Amster Patrick Abbot Jess Adkins Klaus Aktories Toby Allen Ronald Amundson Albert Abbott Elizabeth Adkins-Regan Muhammad Alam James Allison Katrin Amunts Geoff Abbott Roee Admon Eric Alani Mead Allison Myron Amusia Larry Abbott Walter Adriani Pietro Alano Isabel Allona Gynheung An Nicholas Abbott Ruedi Aebersold Cedric Alaux Robin Allshire Zhiqiang An Rasha Abdel Rahman Ueli Aebi Maher Alayyoubi Abigail Allwood Ranjit Anand Zalfa Abdel-Malek Martin Aeschlimann Richard Alba Julian Allwood Beau Ances Minori Abe Ruslan Afasizhev Salim Al-Babili Eric Alm David Andelman Kathryn Abel Markus Affolter Salvatore Albani Benjamin Alman John Anderies Asa Abeliovich Dritan Agalliu Silas Alben Steven Almo Gregor Anderluh John Aber David Agard Mark Alber Douglas Almond Bogi Andersen Geoff Abers Aneel Aggarwal Reka Albert Genevieve Almouzni George Andersen Rohan Abeyaratne Anurag Agrawal R. Craig Albertson Noga Alon Gregers Andersen Susan Abmayr Arun Agrawal Roy Alcalay Uri Alon Ken Andersen Ehab Abouheif Paul Agris Antonio Alcami Claudio Alonso Olaf Andersen Soman Abraham H. -

Annual Scientific Report 2011 Annual Scientific Report 2011 Designed and Produced by Pickeringhutchins Ltd
European Bioinformatics Institute EMBL-EBI Annual Scientific Report 2011 Annual Scientific Report 2011 Designed and Produced by PickeringHutchins Ltd www.pickeringhutchins.com EMBL member states: Austria, Croatia, Denmark, Finland, France, Germany, Greece, Iceland, Ireland, Israel, Italy, Luxembourg, the Netherlands, Norway, Portugal, Spain, Sweden, Switzerland, United Kingdom. Associate member state: Australia EMBL-EBI is a part of the European Molecular Biology Laboratory (EMBL) EMBL-EBI EMBL-EBI EMBL-EBI EMBL-European Bioinformatics Institute Wellcome Trust Genome Campus, Hinxton Cambridge CB10 1SD United Kingdom Tel. +44 (0)1223 494 444, Fax +44 (0)1223 494 468 www.ebi.ac.uk EMBL Heidelberg Meyerhofstraße 1 69117 Heidelberg Germany Tel. +49 (0)6221 3870, Fax +49 (0)6221 387 8306 www.embl.org [email protected] EMBL Grenoble 6, rue Jules Horowitz, BP181 38042 Grenoble, Cedex 9 France Tel. +33 (0)476 20 7269, Fax +33 (0)476 20 2199 EMBL Hamburg c/o DESY Notkestraße 85 22603 Hamburg Germany Tel. +49 (0)4089 902 110, Fax +49 (0)4089 902 149 EMBL Monterotondo Adriano Buzzati-Traverso Campus Via Ramarini, 32 00015 Monterotondo (Rome) Italy Tel. +39 (0)6900 91402, Fax +39 (0)6900 91406 © 2012 EMBL-European Bioinformatics Institute All texts written by EBI-EMBL Group and Team Leaders. This publication was produced by the EBI’s Outreach and Training Programme. Contents Introduction Foreword 2 Major Achievements 2011 4 Services Rolf Apweiler and Ewan Birney: Protein and nucleotide data 10 Guy Cochrane: The European Nucleotide Archive 14 Paul Flicek: -
STB 533. Crystallographic Methods of Structural Biology Course Syllabus and Class Schedule Fall Semester 2014
STB 533. Crystallographic Methods of Structural Biology Course Syllabus and Class Schedule Fall Semester 2014. Class meetings 10:30-11:45 am Tuesdays and Fridays The goal of the course is that students acquire sufficient knowledge and understanding of the basic principles of biomolecular crystal structure analysis that they will be able to comfortably, and with interest and insight, read and comprehend the articles in Volume F of the International Tables for Crystallography: Crystallography of Biological Macromolecules, and articles in the current and recent literature reporting research in structural molecular biology by diffraction methods. Textbooks for the course are: Eaton E. Lattman and Patrick J. Loll (2008). Protein Crystallography: A Concise Guide. Baltimore, Maryland: Johns Hopkins University Press. Bernhard Rupp (2010). Biomolecular Crystallography. Principles, Practice, and Applications to Structural Biology. New York: Garland Science, Taylor and Francis Group, LLC. See also http://www.ruppweb.org/ for valuable supplementary materials. Dates Topics Instructor 26, 29 Aug. Introduction Blessing Protein structural elements 1° aa sequence; 2° α-helix, β strand, β sheet, loop; 3° domain fold; 4° domain assembly. Overview of biomacromolecular crystallography Rupp, chs. 1-4 (Only §§ 1.1-1.5 and 3.2) 2, 5 Sept. Geometrical crystallography Blessing 9, 12 Laws of classical crystallography Lattices, point groups, space groups Crystal faces, lattice planes, and Miller indices The Bragg equation and the Ewald construction Reciprocal space and the reciprocal lattice Rupp, ch. 5 16, 19 Sept. X-Ray diffraction physics Blessing 23, 26 X-Ray sources Wave nature of X-rays X-Ray scattering by an electron, an atom, a molecule by a lattice row, a lattice plane by a crystal – Laue diffraction / Bragg reflection The crystal structure factor Rupp, ch. -

DOUGLAS STENTON ’80 Makes History by Helping Find the H.M.S
DURHAM 40TH ANNIVERSARY INSERT WINTER 2015 46.1 PUBLISHED BY THE TRENT UNIVERSITY ALUMNI ASSOCIATION DOCUMENTING THE HOCKEY HALL OF FAME PETER GZOWSKI COLLEGE 10TH ANNIVERSARY DOUGLAS STENTON ’80 makes history by helping find the H.M.S. Erebus Trent Magazine 46.1 1 Chart the best course for your life in the years ahead. Start with preferred insurance rates. Supporting you... On average, alumni and Trent University. who have home and auto Your needs will change as your life and career evolve. As a Trent University Alumni insurance with us Association member, you have access to save $400.* the TD Insurance Meloche Monnex program, which offers preferred insurance rates, other discounts and great protection, that is easily adapted to your changing needs. Plus, every year our program contributes to supporting your alumni association, so it’s a great way to save and show you care at the same time. Get a quote today! Our extended business hours make it easy. Monday to Friday: 8 a.m. to 8 p.m. Home and auto insurance program recommended by Saturday: 9 a.m. to 4 p.m. HOME | AUTO | TRAVEL Ask for your quote today at 1-888-589-5656 or visit melochemonnex.com/trent The TD Insurance Meloche Monnex program is underwritten by SECURITY NATIONAL INSURANCE COMPANY. It is distributed by Meloche Monnex Insurance and Financial Services Inc. in Quebec, by Meloche Monnex Financial Services Inc. in Ontario, and by TD Insurance Direct Agency Inc. in the rest of Canada. Our address: 50 Place Crémazie, Montreal (Quebec) H2P 1B6. Due to provincial legislation, our auto and recreational vehicle insurance program is not offered in British Columbia, Manitoba or Saskatchewan. -

Crystallography News British Crystallographic Association
Crystallography News British Crystallographic Association Issue No. 112 March 2010 ISSN 1467-2790 Warwick April 2010 p6 BCA AGM 2009 Minutes p12 ECM26 p27 Dr Andrew Booth (1918-2009) p31 The Fankuchen Award p33 Small Molecule & Protein Ready & Protein SuperNova™ The Fastest, Most Intense Dual Wavelength X-ray System Automatic wavelength switching between Mo and Cu X-ray micro-sources 50W X-ray sources provide up to 3x more intensity than a 5kW rotating anode Fastest, highest performance CCD. Large area 135mm Atlas™ or highest sensitivity Eos™ – 330 (e-/X-ray Mo) gain Full 4-circle kappa goniometer AutoChem™, automatic structure solution and refinement software Extremely compact and very low maintenance driving X-ray innovation www.oxford-diffraction.com [email protected] Super Nova ad 1.4.09 - BCA.indd 1 3/4/09 15:38:04 Bruker AXS with DAVINCI. DESIGN The new D8 ADVANCE Designed for the next era in X-ray diffraction DAVINCI.MODE: Real-time component recognition and configuration DAVINCI.SNAP-LOCK: Alignment-free optics change without tools DIFFRAC.DAVINCI: The virtual diffractometer TWIN/TWIN SETUP: Push-button switch between Bragg-Brentano and parallel-beam geometries TWIST-TUBE: Fast and easy switching from line to point focus XRD Order Number DOC-P88-EXS071 © 2009 Bruker AXS GmbH. Printed in Germany. in Germany. AXS GmbH. Printed © 2009 Order Number DOC-P88-EXS071 Bruker think forward Crystallography News March 2010 Contents From the Editor . 2 Council Members . 3 BCA Administrative Office, From the President. 4 David Massey Northern Networking Events Ltd. Puzzle Corner and Corporate Members . 5 Glenfinnan Suite, Braeview House 9/11 Braeview Place East Kilbride G74 3XH BCA AGM 2010. -

An Exploration of Some Aspects of Molecular Replacement in Macromolecular Crystallography
An exploration of some aspects of molecular replacement in macromolecular crystallography Richard Mifsud Christ’s College Submitted: June 2018 This dissertation is submitted for the degree of Doctor of Philosophy Declarations This dissertation is the result of my own work and includes nothing which is the outcome of work done in collaboration except as declared in the Preface and specified in the text. It is not substantially the same as any that I have submitted, or, is being concurrently submitted for a degree or diploma or other qualification at the University of Cambridge or any other University or similar institution except as declared in the Preface and specified in the text. I further state that no substantial part of my dissertation has already been submitted, or, is being concurrently submitted for any such degree, diploma or other qualification at the University of Cambridge or any other University or similar institution except as declared in the Preface and specified in the text. It does not exceed the prescribed word limit for the relevant Degree Committee. 1 Acknowledgements I would like to thank all those who helped fund my research that greatly increased my understanding of this field, allowed me to contribute to the wealth of knowledge, and enabled me to generate this thesis. I have been on the Cambridge Institute for Medical Research 4 year PhD Programme, funded by the Wellcome Trust. I would like to thank INSTRUCT for granting a travel fellowship to allow me to attend the Gordon Research Conference on structural biology in 2014. I would like to give thanks to Professor Randy Read for allowing me to do a Doctor of Philosophy project in his group. -
Crystallography in the News New Product Introduction: Rigaku
Protein Crystallography Newsletter Volume 6, No. 5, May 2014 Crystallography in the news In this issue: May 3, 2014. A research team led by Professor Jennifer Potts, a British Heart Foundation Senior Research Fellow in York's Department of Biology, studied how Staphylococcus Crystallography in the news aureus attach to two proteins fibronectin and fibrinogen found in human blood. News: IUCr 23rd Congress May 4, 2014. Arizona State University scientists, together with collaborators from the Science video of the month Chinese Academy of Sciences in Shanghai, have published a first of its kind atomic level Upcoming events look at the enzyme telomerase that may unlock the secrets to the fountain of youth. Product spotlight: BioSAXS-2000 Crystallographers in the news May 7, 2014. Soon the Advanced Photon Source (APS) will get a boost in efficiency that likely will translate into a big boon for the discovery of new pharmaceuticals. The world's Scientist spotlight: Susan Buchanan first protein characterization research facility directly attached to a light source will open Useful links for crystallography in the near future at the APS. The Advanced Protein Characterization Facility (APCF) will Survey of the month use state-of-the-art robotics for gene cloning, protein expression, protein purification and protein crystallization. Recent crystallographic papers Book reviews May 12, 2014. Google honors Dorothy Hodgkin's X-ray vision with a molecular doodle. The event marks the 104th anniversary of the British chemist, who pioneered the use of X- rays to determine the structure of biological molecules. Special News Item IUCr 23rd Congress May 13, 2014. -
Short Program.Pdf
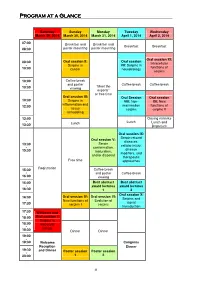
Program at a Glance Saturday Sunday Monday Tuesday Wednesday March 29, 2014 March 30, 2014 March 31, 2014 April 1, 2014 April 2, 2014 07:00 Breakfast and Breakfast and - Breakfast Breakfast 08:30 poster mounting poster mounting Oral session XI: Oral session II: Oral session 08:30 Intracellular - Serpins in VII: Serpins in functions of 10:00 cancer neurobiology serpins 10:00 Coffee break - and poster Coffee break Coffee break “Meet the 10:30 viewing experts” or free time Oral session III: Oral Session Oral session 10:30 Serpins in VIII: Non- XII: New - inflammation and 12:00 mammalian functions of tissue serpins serpins II remodeling 12:00 Closing remarks - Lunch Lunch Lunch and 13:30 Departure Oral session IX: Serpin-related Oral session V: diseases: Serpin 13:30 cellular injury, - conformation, disease 15:30 maturation, modifiers, and and/or disposal therapeutic Free time approaches Registration 15:30 Coffee break - and poster Coffee break 16:00 viewing 16:00 Best abstract Best abstract - award lectures award lectures 16:30 1 2 Oral session X : Oral session IV: Oral session VI: 16:30 Serpins and - New functions of Evolution of signal 17:30 serpins I serpins transduction 17:30 Welcome and - 18:00 Oral session I: Serpins in 18:00 leucocyte - biology 18:30 Dinner Dinner 19:00 - 19:30 Welcome Congress Reception Dinner 19:30 and Dinner Poster session Poster session - 23:00 1 2 8 Specific program March 29 ththth , 2014 Saturday, March 29 th , 2014 17:30-17:45 Welcome Oral session I: Serpins in leucocyte biology Chairperson: Alireza R. -

From Crystal to Structure with CCP4
This is a repository copy of From crystal to structure with CCP4. White Rose Research Online URL for this paper: http://eprints.whiterose.ac.uk/128311/ Version: Published Version Article: Hough, Michael A. and Wilson, Keith S. orcid.org/0000-0002-3581-2194 (2018) From crystal to structure with CCP4. Acta crystallographica. Section D, Structural biology. D74, 67. ISSN 2059-7983 https://doi.org/10.1107/S2059798317017557 Reuse Items deposited in White Rose Research Online are protected by copyright, with all rights reserved unless indicated otherwise. They may be downloaded and/or printed for private study, or other acts as permitted by national copyright laws. The publisher or other rights holders may allow further reproduction and re-use of the full text version. This is indicated by the licence information on the White Rose Research Online record for the item. Takedown If you consider content in White Rose Research Online to be in breach of UK law, please notify us by emailing [email protected] including the URL of the record and the reason for the withdrawal request. [email protected] https://eprints.whiterose.ac.uk/ introduction From crystal to structure with CCP4 Michael A. Hougha* and Keith S. Wilsonb* ISSN 2059-7983 aSchool of Biological Sciences, University of Essex, Wivenhoe Park, Colchester, CO4 3SQ, UK, and bYork Structural Biology Laboratory, University of York, Heslington, York, YO10 5DD, UK. *Correspondence e-mail: [email protected], [email protected] The 2017 CCP4 Study Weekend was held at the University of Nottingham with the title From Crystal to Structure.