An Information Theoretical Method for Analyzing Unreplicated Designs with Binary Response
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

A Nonparametric Estimator of Heterogeneity Variance with Applications to SMR- and Proportion-Data
Biometrical Journal 42 )2000) 3, 321±334 A Nonparametric Estimator of Heterogeneity Variance with Applications to SMR- and Proportion-Data Dankmar BoÈhning Department of Epidemiology Institute for Social Medicine and Medical Psychology Free University Berlin Germany Jesus Sarol Jr. Department of Epidemiology and Biostatistics The College of Public Health University of the Philippines Manila Philippines Summary In this paper the situation of extra population heterogeneity is discussed from a analysis of variance point of view. We first provide a non-iterative way of estimating the variance of the heterogeneity distribution without estimating the heterogeneity distribution itself for Poisson and binomial counts. The consequences of the presence of heterogeneity in the estimation of the mean are discussed. We show that if the homogeneity assumption holds, the pooled mean is optimal while in the presence of strong heterogeneity, the simple )arithmetic) mean is an optimal estimator of the mean SMR or mean proportion. These results lead to the problem of finding an optimal estimator for situations not repre- sented by these two extreme cases. We propose an iterative solution to this problem. Illustrations for the application of these findings are provided with examples from various areas. Key words: Population heterogeneity; Random effects model; Moment estimator; Variance separation; Confidence interval estimation adjusted for unob- served heterogeneity. 1. Introduction In a variety of biometric applications the situation of extra-population heteroge- neity occurs. In particular, this is the case if there is good reason to model the variable of interest Y through a density of parametric form p)y, q) with a scalar parameter q. -

A Simple Method for Correcting for the Will Rogers Phenomenon with Biometrical Applications
University of Plymouth PEARL https://pearl.plymouth.ac.uk Faculty of Science and Engineering School of Engineering, Computing and Mathematics 2020-01-20 A simple method for correcting for the Will Rogers phenomenon with biometrical applications Stander, M http://hdl.handle.net/10026.1/15227 10.1002/bimj.201900199 Biometrical Journal: journal of mathematical methods in biosciences Wiley-VCH Verlag All content in PEARL is protected by copyright law. Author manuscripts are made available in accordance with publisher policies. Please cite only the published version using the details provided on the item record or document. In the absence of an open licence (e.g. Creative Commons), permissions for further reuse of content should be sought from the publisher or author. Biometrical Journal 52 (2010) 61, zzz–zzz / DOI: 10.1002/bimj.200100000 A simple method for correcting for the Will Rogers phenomenon with biometrical applications Mark Stander∗ 1 and Julian Stander 2 1 BAE Systems 6 Carlton Gardens LONDON SW1Y 5AD United Kingdom Email: [email protected] 2 School of Engineering, Computing and Mathematics University of Plymouth Drake Circus PLYMOUTH PL4 8AA United Kingdom Email: [email protected] Received zzz, revised zzz, accepted zzz In its basic form the Will Rogers phenomenon takes place when an increase in the average value of each of two sets is achieved by moving an element from one set to another. This leads to the conclusion that there has been an improvement, when in fact essentially nothing has changed. Extended versions of this phenomenon can occur in epidemiological studies, rendering their results unreliable. -

Rank Full Journal Title Journal Impact Factor 1 Journal of Statistical
Journal Data Filtered By: Selected JCR Year: 2019 Selected Editions: SCIE Selected Categories: 'STATISTICS & PROBABILITY' Selected Category Scheme: WoS Rank Full Journal Title Journal Impact Eigenfactor Total Cites Factor Score Journal of Statistical Software 1 25,372 13.642 0.053040 Annual Review of Statistics and Its Application 2 515 5.095 0.004250 ECONOMETRICA 3 35,846 3.992 0.040750 JOURNAL OF THE AMERICAN STATISTICAL ASSOCIATION 4 36,843 3.989 0.032370 JOURNAL OF THE ROYAL STATISTICAL SOCIETY SERIES B-STATISTICAL METHODOLOGY 5 25,492 3.965 0.018040 STATISTICAL SCIENCE 6 6,545 3.583 0.007500 R Journal 7 1,811 3.312 0.007320 FUZZY SETS AND SYSTEMS 8 17,605 3.305 0.008740 BIOSTATISTICS 9 4,048 3.098 0.006780 STATISTICS AND COMPUTING 10 4,519 3.035 0.011050 IEEE-ACM Transactions on Computational Biology and Bioinformatics 11 3,542 3.015 0.006930 JOURNAL OF BUSINESS & ECONOMIC STATISTICS 12 5,921 2.935 0.008680 CHEMOMETRICS AND INTELLIGENT LABORATORY SYSTEMS 13 9,421 2.895 0.007790 MULTIVARIATE BEHAVIORAL RESEARCH 14 7,112 2.750 0.007880 INTERNATIONAL STATISTICAL REVIEW 15 1,807 2.740 0.002560 Bayesian Analysis 16 2,000 2.696 0.006600 ANNALS OF STATISTICS 17 21,466 2.650 0.027080 PROBABILISTIC ENGINEERING MECHANICS 18 2,689 2.411 0.002430 BRITISH JOURNAL OF MATHEMATICAL & STATISTICAL PSYCHOLOGY 19 1,965 2.388 0.003480 ANNALS OF PROBABILITY 20 5,892 2.377 0.017230 STOCHASTIC ENVIRONMENTAL RESEARCH AND RISK ASSESSMENT 21 4,272 2.351 0.006810 JOURNAL OF COMPUTATIONAL AND GRAPHICAL STATISTICS 22 4,369 2.319 0.008900 STATISTICAL METHODS IN -

Abbreviations of Names of Serials
Abbreviations of Names of Serials This list gives the form of references used in Mathematical Reviews (MR). ∗ not previously listed The abbreviation is followed by the complete title, the place of publication x journal indexed cover-to-cover and other pertinent information. y monographic series Update date: January 30, 2018 4OR 4OR. A Quarterly Journal of Operations Research. Springer, Berlin. ISSN xActa Math. Appl. Sin. Engl. Ser. Acta Mathematicae Applicatae Sinica. English 1619-4500. Series. Springer, Heidelberg. ISSN 0168-9673. y 30o Col´oq.Bras. Mat. 30o Col´oquioBrasileiro de Matem´atica. [30th Brazilian xActa Math. Hungar. Acta Mathematica Hungarica. Akad. Kiad´o,Budapest. Mathematics Colloquium] Inst. Nac. Mat. Pura Apl. (IMPA), Rio de Janeiro. ISSN 0236-5294. y Aastaraam. Eesti Mat. Selts Aastaraamat. Eesti Matemaatika Selts. [Annual. xActa Math. Sci. Ser. A Chin. Ed. Acta Mathematica Scientia. Series A. Shuxue Estonian Mathematical Society] Eesti Mat. Selts, Tartu. ISSN 1406-4316. Wuli Xuebao. Chinese Edition. Kexue Chubanshe (Science Press), Beijing. ISSN y Abel Symp. Abel Symposia. Springer, Heidelberg. ISSN 2193-2808. 1003-3998. y Abh. Akad. Wiss. G¨ottingenNeue Folge Abhandlungen der Akademie der xActa Math. Sci. Ser. B Engl. Ed. Acta Mathematica Scientia. Series B. English Wissenschaften zu G¨ottingen.Neue Folge. [Papers of the Academy of Sciences Edition. Sci. Press Beijing, Beijing. ISSN 0252-9602. in G¨ottingen.New Series] De Gruyter/Akademie Forschung, Berlin. ISSN 0930- xActa Math. Sin. (Engl. Ser.) Acta Mathematica Sinica (English Series). 4304. Springer, Berlin. ISSN 1439-8516. y Abh. Akad. Wiss. Hamburg Abhandlungen der Akademie der Wissenschaften xActa Math. Sinica (Chin. Ser.) Acta Mathematica Sinica. -

Curriculum Vitae
Curriculum Vitae PERSONAL INFORMATION Norbert Benda WORK EXPERIENCE February 2010- Present Head of Biostatistics and Special Pharmacokinetics Unit BfArM (Federal Institute for Drugs and Medical Devices) (Germany) Managing Biostatistics and Special Pharmacokinetics Unit, biostatistical assessment of European and national German drug applications, biostatistical support in scientific advices, biostatistical input to guidelines, biostatistical input to clinical and methodological research projects November 2006-January 2010 (Senior) Expert Statistical Methodologist Novartis Pharma AG (Switzerland) Development and application of novel statistical methodologies (dose-finding, adaptive designs, longitudinal data analysis, missing data, optimal design), methodological support for Trial and Program Statisticians, clinical scenario evaluations (simulations) for clinical trial planning, internal training courses in statistics July 1997-October 2006 Statistician Schering AG (Germany) Statistical design and analysis of clinical studies (phase I - IV), statistical consultant for preclinical and clinical development, project statistician for international drug development projects, member of the Global Pharmacometrics Team October 1993-July 1997 Research Assistant University of Tübingen, Department of Medical Biometry (Germany) Statistical consultant in statistics for medical PhD students and researchers, lectures in medical statistics, design and evaluation of medical studies, research projects in ophthalmology April 1989-September 1993 Research Assistant -

Joshua M. Tebbs
Joshua M. Tebbs Department of Statistics 215C LeConte College University of South Carolina Columbia, SC 29208 USA tel: +1 803 576-8765 fax: +1 803 777-4048 email: [email protected] www: http://people.stat.sc.edu/tebbs/ Date and Place of Birth: 1973; Fort Madison, Iowa, USA Degrees 2000 Ph.D., Statistics, North Carolina State University Advisor: William H. Swallow 1997 M.S., Statistics, University of Iowa 1995 B.S., Mathematics, Statistics; Honors: Statistics; Minor: Spanish, University of Iowa Professional Experience 2012- Professor, Department of Statistics, University of South Carolina 2010-2012 Graduate Director, Department of Statistics, University of South Carolina 2008-2011 Associate Professor, Department of Statistics, University of South Carolina 2006-2009 Undergraduate Director, Department of Statistics, University of South Carolina 2005-2008 Assistant Professor, Department of Statistics, University of South Carolina 2004-2005 Undergraduate Director, Department of Statistics, Kansas State University 2003-2005 Assistant Professor, Department of Statistics, Kansas State University 2001-2003 Assistant Professor, Department of Statistics, Oklahoma State University 2000-2001 Statistician, United Technologies 1997-2000 Teaching Assistant, Department of Statistics, North Carolina State University 1995-1997 Teaching Assistant, Department of Statistics, University of Iowa Current Research Interests Categorical data, statistical methods for pooled data (group testing), order-restricted inference, applications in epidemiology and public -

Sanat K. Sarkar Cyrus
September 2019 Sanat K. Sarkar Cyrus. H. K. Curtis Professor and Chair Department of Statistical Science Temple University http://sites.temple.edu/sanat/ https://scholar.google.com/citations?user=FtID5t0AAAAJ&hl=en https://www.researchgate.net/profile/Sanat_Sarkar Experience ACADEMIC 2016 – Full Professor, Department of Statistical Science, Temple University, Philadelphia, PA 1994 - 2016 Full Professor, Department of Statistics, Temple University, Philadelphia, PA 1988 - 1994 Associate Professor, Department of Statistics, Temple University, Philadelphia, PA 1983 - 1988 Assistant Professor, Department of Statistics, Temple University, Philadelphia, PA 1982 - 1983 Adjunct Assistant Professor, Department of Statistics, Temple University, Philadelphia, PA 1980 - 1982 Research Associate, Department of Mathematics and Statistics, University of Pittsburgh, Pittsburgh, PA 1976 - 1980 Lecturer, Department of Statistics, Calcutta University, Calcutta, India NON-ACADEMIC 2019- Member, Advisory Board, Prosoft Clinical and LogEcal Data Analytics, Wayne, PA 2008 Member, Scientific Advisory Committee, Merck Research Labs, 2007 Statistical Consultant, Novartis Pharmaceuticals 2006 Statistical Consultant, Cephalon Inc. 1991 - 2000 Statistical Consultant, Merck Research Lab, Blue Bell, PA Summer, 1991 Senior Biometrician, Merck Research Lab, Blue Bell, PA Summer, 1986 Visiting Scientist, Epi-Stat Research Lab, Fox Chase Cancer Research Center, Philadelphia, PA Professional Societies • Calcutta Statistical Association (Life member) • International Indian -

Classifying Antibodies Using Flow Cytometry Data: Class Prediction and Class Discovery
Biometrical Journal 47 (2005) 5, 740--754 DOI: 10.1002/bimj.200310142 Classifying Antibodies Using Flow Cytometry Data: Class Prediction and Class Discovery M. P. Salganik*; 1, E. L. Milford2, D. L. Hardie3, S. Shaw4, and M. P. Wand5 1 Department of Biostatistics, Harvard School of Public Health, 665 Huntington Avenue, Boston, MA, 02115, USA 2 Department of Medicine, Brigham and Women’s Hospital, Harvard Medical School, Boston, MA, 02115, USA 3 MRC Centre for Immune Regulation, Institute of Biomedical Research, University of Birmingham, Birmingham 2TT, UK 4 Experimental Immunology Branch, National Cancer Institute, National Institute of Health, Bethesda, MD 20892-1360, USA 5 Department of Statistics, School of Mathematics, University of New South Wales, Sydney, 2052, Australia Received 21 October 2003, revised 14 January 2005, accepted 16 March 2005 Summary Classifying monoclonal antibodies, based on the similarity of their binding to the proteins (antigens) on the surface of blood cells, is essential for progress in immunology, hematology and clinical medicine. The collaborative efforts of researchers from many countries have led to the classification of thousands of antibodies into 247 clusters of differentiation (CD). Classification is based on flow cytometry and biochemical data. In preliminary classifications of antibodies based on flow cytometry data, the object requiring classification (an antibody) is described by a set of random samples from unknown densities of fluorescence intensity. An individual sample is collected in the experiment, where a population of cells of a certain type is stained by the identical fluorescently marked replicates of the antibody of interest. Samples are collected for multiple cell types. -
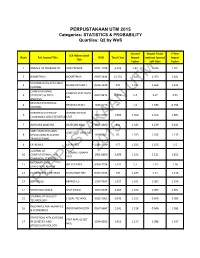
PERPUSTAKAAN UTM 2015 Categories: STATISTICS & PROBABILITY Quartiles: Q2 by Wos
PERPUSTAKAAN UTM 2015 Categories: STATISTICS & PROBABILITY Quartiles: Q2 by WoS Journal Impact Factor 5-Year JCR Abbreviated Rank Full Journal Title ISSN Total Cites Impact without Journal Impact Title Factor Self Cites Factor 1 ANNALS OF PROBABILITY ANN PROBAB 0091-1798 4,226 1.42 1.326 1.701 2 BIOMETRIKA BIOMETRIKA 0006-3444 15,774 1.418 1.359 2.281 SCANDINAVIAN ACTUARIAL 3 SCAND ACTUAR J 0346-1238 370 1.412 1.265 1.212 JOURNAL COMPUTATIONAL COMPUT STAT DATA UTM 4 STATISTICS & DATA 0167-9473 6,012 1.4 1.07 1.51 AN ANALYSIS REVSTAT-STATISTICAL 4 REVSTAT-STAT J 1645-6726 92 1.4 1.333 0.794 JOURNAL OXFORD BULLETIN OF OXFORD B ECON 6 0305-9049 1,986 1.368 1.356 1.885 ECONOMICS AND STATISTICS STAT 7 BAYESIAN ANALYSIS BAYESIAN ANAL 1931-6690 841 1.343 1.239 2.443 SORT-STATISTICS AND SORT-STAT OPER RES 8 OPERATIONS RESEARCH 1696-2281 85 1.333 1.292 1.133 T TRANSACTIONS 8 EXTREMES EXTREMES 1386-1999 457 1.333 1.156 1.5 JOURNAL OF J COMPUT GRAPH 2015 10 COMPUTATIONAL AND 1061-8600 2,699 1.222 1.121 1.812 STAT GRAPHICAL STATISTICS INTERNATIONAL 11 INT STAT REV 0306-7734 1,131 1.2 1.15 1.28 STATISTICAL REVIEW 12 ECONOMETRIC REVIEWS ECONOMET REV 0747-4938 730 1.189 1.17 1.116 13 BERNOULLIPERPUSTAKAANBERNOULLI 1350-7265 1,327 1.161 1.083 1.296 14 STATISTICA SINICA STAT SINICA 1017-0405 2,269 1.158 1.099 1.591 JOURNAL OF QUALITY 15 J QUAL TECHNOL 0022-4065 2,046 1.152 0.848 2.096 TECHNOLOGY INSURANCE MATHEMATICS 16 INSUR MATH ECON 0167-6687 2,141 1.128 0.646 1.582 & ECONOMICS STATISTICAL APPLICATIONS STAT APPL GENET 17 IN GENETICS AND 2194-6302 1,415 -

Bounds for the Weight of External Data in Shrinkage Estimation
Biometrical Journal XX (2020) YY, zzz–zzz / DOI: 10.1002/bimj.DOIsuffix Bounds for the weight of external data in shrinkage estimation ,1 1 Christian Rover¨ ∗ and Tim Friede 1 Department of Medical Statistics, University Medical Center G¨ottingen, Humboldtallee 32, 37073 G¨ottingen, Germany Received xxx, revised yyy, accepted zzz Shrinkage estimation in a meta-analysis framework may be used to facilitate dynamical borrowing of infor- mation. This framework might be used to analyze a new study in the light of previous data, which might differ in their design (e.g., a randomized controlled trial (RCT) and a clinical registry). We show how the common study weights arise in effect and shrinkage estimation, and how these may be generalized to the case of Bayesian meta-analysis. Next we develop simple ways to compute bounds on the weights, so that the contribution of the external evidence may be assessed a priori. These considerations are illustrated and dis- cussed using numerical examples, including applications in the treatment of Creutzfeldt-Jakob disease and in fetal monitoring to prevent the occurrence of metabolic acidosis. The target study’s contribution to the re- sulting estimate is shown to be bounded below. Therefore, concerns of evidence being easily overwhelmed by external data are largely unwarranted. Key words: Random-effects meta-analysis; Bayesian statistics; Between-study heterogeneity; Shrinkage estimation; Inverse-variance weights. 1 Introduction In some situations it is useful to support an estimate using additional external evidence, for example, when a small study in the context of a rare disease may be supplemented with data from a clinical registry or electronic health records, or when the result from a meta-analysis may be backed by an analysis in a sim- ilar field, e.g., a related but somewhat different population. -
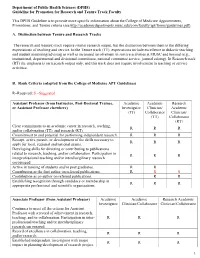
On Switching from Research to Tenure Track
Department of Public Health Sciences (DPHS) Guideline for Promotion for Research and Tenure Track Faculty This DPHS Guideline is to provide more specific information about the College of Medicine Appointments, Promotions, and Tenure criteria (see http://academicdepartments.musc.edu/com/faculty/apt/forms/guidelines.pdf). A. Distinction between Tenure and Research Tracks The research and (tenure) track require similar research output, but the distinction between them is the differing expectations of teaching and service. In the Tenure track (TT), expectations include excellence in didactic teaching and student mentoring/advising as well as increased involvement in service activities at MUSC and beyond (e.g., institutional, departmental and divisional committees, national committee service, journal editing). In Research track (RT) the emphasis is on research output only, and this track does not require involvement in teaching or service activities. B. Rank Criteria (adapted from the College of Medicine APT Guidelines) R=Required; S =Suggested Assistant Professor (from Instructor, Post-Doctoral Trainee, Academic Academic Research or Assistant Professor elsewhere) Investigator Clinician/ Academic (TT) Collaborator Clinician/ (TT) Collaborator (RT) Clear commitment to an academic career in research, teaching, R R R and/or collaboration (TT), and research (RT) Commitment to and potential for performing independent research. R R R Receipt, active pursuit, or development of the skills necessary to R R R apply for local, regional and national grants. Developing skills for directing or contributing to publications related to research, teaching, and/or collaboration. Participation in R R R interprofessional teaching and/or interdisciplinary research encouraged. Active in training of students and/or post graduates. -
Statistics Promotion and Tenure Guidelines
Approved by Department 12/05/2013 Approved by Faculty Relations May 20, 2014 UFF Notified May 21, 2014 Effective Spring 2016 2016-17 Promotion Cycle Department of Statistics Promotion and Tenure Guidelines The purpose of these guidelines is to give explicit definitions of what constitutes excellence in teaching, research and service for tenure-earning and tenured faculty. Research: The most common outlet for scholarly research in statistics is in journal articles appearing in refereed publications. Based on the five-year Impact Factor (IF) from the ISI Web of Knowledge Journal Citation Reports, the top 50 journals in Probability and Statistics are: 1. Journal of Statistical Software 26. Journal of Computational Biology 2. Econometrica 27. Annals of Probability 3. Journal of the Royal Statistical Society 28. Statistical Applications in Genetics and Series B – Statistical Methodology Molecular Biology 4. Annals of Statistics 29. Biometrical Journal 5. Statistical Science 30. Journal of Computational and Graphical Statistics 6. Stata Journal 31. Journal of Quality Technology 7. Biostatistics 32. Finance and Stochastics 8. Multivariate Behavioral Research 33. Probability Theory and Related Fields 9. Statistical Methods in Medical Research 34. British Journal of Mathematical & Statistical Psychology 10. Journal of the American Statistical 35. Econometric Theory Association 11. Annals of Applied Statistics 36. Environmental and Ecological Statistics 12. Statistics in Medicine 37. Journal of the Royal Statistical Society Series C – Applied Statistics 13. Statistics and Computing 38. Annals of Applied Probability 14. Biometrika 39. Computational Statistics & Data Analysis 15. Chemometrics and Intelligent Laboratory 40. Probabilistic Engineering Mechanics Systems 16. Journal of Business & Economic Statistics 41. Statistica Sinica 17.