Complex Variables with Applications Department of Mathematics at CU
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Administrator's Guide
Trend Micro Incorporated reserves the right to make changes to this document and to the product described herein without notice. Before installing and using the product, review the readme files, release notes, and/or the latest version of the applicable documentation, which are available from the Trend Micro website at: http://docs.trendmicro.com/en-us/enterprise/scanmail-for-microsoft- exchange.aspx Trend Micro, the Trend Micro t-ball logo, Apex Central, eManager, and ScanMail are trademarks or registered trademarks of Trend Micro Incorporated. All other product or company names may be trademarks or registered trademarks of their owners. Copyright © 2020. Trend Micro Incorporated. All rights reserved. Document Part No.: SMEM149028/200709 Release Date: November 2020 Protected by U.S. Patent No.: 5,951,698 This documentation introduces the main features of the product and/or provides installation instructions for a production environment. Read through the documentation before installing or using the product. Detailed information about how to use specific features within the product may be available at the Trend Micro Online Help Center and/or the Trend Micro Knowledge Base. Trend Micro always seeks to improve its documentation. If you have questions, comments, or suggestions about this or any Trend Micro document, please contact us at [email protected]. Evaluate this documentation on the following site: https://www.trendmicro.com/download/documentation/rating.asp Privacy and Personal Data Collection Disclosure Certain features available in Trend Micro products collect and send feedback regarding product usage and detection information to Trend Micro. Some of this data is considered personal in certain jurisdictions and under certain regulations. -

Windows X32 Cross Compile Guide
Guide for cross compiling Trezarcoin for windows. By Iwens Fortis Tested on Ubuntu 16.04.2 LTS. • Start on ubuntu your terminal (search for terminal with ubuntu dash top icon left, or press windows key to open dash). • First we need to install the dependencies, for this execute the following cmd’s stated below in the terminal window. The commands to execute are in the grey textboxes. The commands will ask for a password which and u have to confirm some commands with y from yes. Tip transfer the pdf to ubuntu for easy copy and paste. • First update the apt library. sudo apt-get update • Install needed dependencies to install mxe to cross compile Trezarcoin. sudo apt-get install p7zip-full autoconf automake autopoint bash bison bzip2 cmake flex gettext git g++ gperf intltool \ libffi-dev libtool libltdl-dev libssl-dev libxml-parser-perl make openssl patch perl pkg-config python ruby scons sed unzip \ wget xz-utils libtool-bin libgdk-pixbuf2.0-dev g++-multilib libc6-dev-i386 upx -y • We need to get latest mxe from github and compile libraries needed. git clone https://github.com/mxe/mxe.git cd mxe make MXE_TARGETS="i686-w64-mingw32.static" boost make MXE_TARGETS="i686-w64-mingw32.static" qttools make MXE_TARGETS="i686-w64-mingw32.static" miniupnpc • Next we need to compile the recommended Berkeley DB our self cd ~ wget 'http://download.oracle.com/berkeley-db/db-4.8.30.NC.tar.gz' tar zxvf db-4.8.30.NC.tar.gz cd db-4.8.30.NC • Now we will create a bash script for this execute the following commands to create the bash script. -

Command-Line Guide for Linux, Mac & Windows
Command-line Guide for Linux, Mac & Windows info.nrao.edu /computing/guide/file-access-and-archiving/7zip/7z-7za-command-line-guide See also: File Archiving and Compression, Accessing and Sharing Files, Network Access, Windows Terminal Servers 7-Zip Versions 7-Zip is an Archive and File Management utility available in command-line versions for Linux/Mac, "P7Zip" (7z.exe), as well as for Windows, "7za" (7za.exe). Although its interface is deceptively simple, the command-line versions of 7ZIP are highly customizable archiving programs when used with the command parameters and switchesdescribed below. Windows users who want to use the command-line version should generate a Help Desk ticket to install the standalone 7za.exe version. To begin a session, open a terminal window. Invoke the version of 7Zip you are using by entering " 7z" for P7Zip (7z.exe), or "7za" for 7Zip for Windows (7za.exe) to start either the P7-Zip or 7za application prior to entering commands. Other than this program invocation command, all commands, parameters and switches are identical for all command-line versions. NOTE TO WINDOWS USERS: the following syntax examples begin by invoking the Linux command-line version, "7z". Please change the invocation to "7za" when applying these examples for use in 7-Zip for Windows. Command Line Syntax The general command line syntax begins by invoking the version of 7Zip you are using: "7z" for P7Zip (7z.exe) users or "7za" for 7Zip for Windows (7za.exe) users followed by the command and parameters: "command" "switches" "full_path_archive_name" "full_path_file_name" Eg; 7z a -p 7Zip_Archive Test_file.txt creates a 7z formatted archive named 7Zip_Archive that is protected with a password , then adds a file named test_file.txt to the archive. -
3. PE Portable Executable: a Look
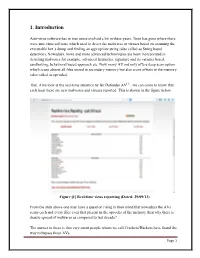
1. Introduction Anti-virus software has in true sense evolved a lot in these years. Time has gone where there were anti-virus software which used to detect the malwares or viruses based on scanning the executable hex`s dump and finding an appropriate string (also called as String based detection). Nowadays, more and more advanced technologies are been incorporated in detecting malwares for example, advanced heuristics, signature and its variants based, sandboxing, behavioral based approach etc. Now many AV not only offers deep scan option which scans almost all files stored in secondary memory but also scans offsets in the memory (also called as opcodes). But, if we look at the real-time statistics by Bit Defender AV[1] , we can come to know that each hour there are new malwares and viruses reported. This is shown in the figure below. Figure [1] Real-time virus reporting (Dated: 29/09/13) From the stats above one may have a question rising in their mind that nowadays the AVs scans each and every files even that present in the opcodes of the memory then why there is drastic spread of malwares as compared to last decade? The answer to these is that very smart people whom we call Crackers/Hackers have found the way to bypass these AVs. Page 1 They know the very detail about how the AV works and which AV have which type of detection capabilities for example if it scans based on string detection or if it scans based on sandboxing approach. We sometimes fail to remember that they (Crackers and Hackers) too have AV scanners from which they may scan their newly developed malware and viruses and can easily spread via plethora of medium, mostly the Internet. -

Qualitative and Quantitative Evaluation of Software Packers
Qualitative and Quantitative Evaluation of Software Packers Mar´ıa Bazus,´ Ricardo J. Rodr´ıguez, Jose´ Merseguer « All wrongs reversed [email protected] ¸ @RicardoJRdez ¸ www.ricardojrodriguez.es Department of Computer Science and Systems Engineering University of Zaragoza, Spain December 12, 2015 NoConName 2015 Barcelona (Spain) $whoami Ph.D. on Comp. Sci. (Univ. of Zaragoza, Spain) (2013) Assistant Professor at University of Zaragoza Performance analysis on critical, complex systems Secure Software Engineering Advance malware analysis RFID/NFC Security Not prosecuted ^¨ Speaker at NcN, HackLU, RootedCON, STIC CCN-CERT, HIP, MalCON, HITB. M. Bazus,´ R.J. Rodr´ıguez, J. Merseguer Qualitative and Quantitative Evaluation of Software Packers NcN 2015 2 / 39 Agenda 1 Introduction 2 Contributions and Related Work 3 Previous Concepts 4 Software Protection Taxonomy 5 Software Packers Under Study 6 Qualitative and Quantitative Evaluation Qualitative Evaluation Quantitative Evaluation 7 Conclusions and Future Work M. Bazus,´ R.J. Rodr´ıguez, J. Merseguer Qualitative and Quantitative Evaluation of Software Packers NcN 2015 3 / 39 Agenda 1 Introduction 2 Contributions and Related Work 3 Previous Concepts 4 Software Protection Taxonomy 5 Software Packers Under Study 6 Qualitative and Quantitative Evaluation Qualitative Evaluation Quantitative Evaluation 7 Conclusions and Future Work M. Bazus,´ R.J. Rodr´ıguez, J. Merseguer Qualitative and Quantitative Evaluation of Software Packers NcN 2015 4 / 39 RE uses: legitimate and illegitimate X Find software bugs X Get interoperability with legacy systems X Detect malicious software X Detect vulnerabilities to create/spread malware X Obtain (or avoid) software license duplication Introduction (I): Reverse Engineering WTF? To analyse a binary program with machine-code vision Types of analysis: Static analysis( + not executed, * all paths explored) Dynamic analysis( * truly executed, + but just one path explored!) M. -

Kafl: Hardware-Assisted Feedback Fuzzing for OS Kernels
kAFL: Hardware-Assisted Feedback Fuzzing for OS Kernels Sergej Schumilo1, Cornelius Aschermann1, Robert Gawlik1, Sebastian Schinzel2, Thorsten Holz1 1Ruhr-Universität Bochum, 2Münster University of Applied Sciences Motivation IJG jpeg libjpeg-turbo libpng libtiff mozjpeg PHP Mozilla Firefox Internet Explorer PCRE sqlite OpenSSL LibreOffice poppler freetype GnuTLS GnuPG PuTTY ntpd nginx bash tcpdump JavaScriptCore pdfium ffmpeg libmatroska libarchive ImageMagick BIND QEMU lcms Adobe Flash Oracle BerkeleyDB Android libstagefright iOS ImageIO FLAC audio library libsndfile less lesspipe strings file dpkg rcs systemd-resolved libyaml Info-Zip unzip libtasn1OpenBSD pfctl NetBSD bpf man mandocIDA Pro clamav libxml2glibc clang llvmnasm ctags mutt procmail fontconfig pdksh Qt wavpack OpenSSH redis lua-cmsgpack taglib privoxy perl libxmp radare2 SleuthKit fwknop X.Org exifprobe jhead capnproto Xerces-C metacam djvulibre exiv Linux btrfs Knot DNS curl wpa_supplicant Apple Safari libde265 dnsmasq libbpg lame libwmf uudecode MuPDF imlib2 libraw libbson libsass yara W3C tidy- html5 VLC FreeBSD syscons John the Ripper screen tmux mosh UPX indent openjpeg MMIX OpenMPT rxvt dhcpcd Mozilla NSS Nettle mbed TLS Linux netlink Linux ext4 Linux xfs botan expat Adobe Reader libav libical OpenBSD kernel collectd libidn MatrixSSL jasperMaraDNS w3m Xen OpenH232 irssi cmark OpenCV Malheur gstreamer Tor gdk-pixbuf audiofilezstd lz4 stb cJSON libpcre MySQL gnulib openexr libmad ettercap lrzip freetds Asterisk ytnefraptor mpg123 exempi libgmime pev v8 sed awk make -

0Wning Antivirus Alex Wheeler ([email protected]) Neel Mehta ([email protected]) Why AV?
0wning Antivirus Alex Wheeler ([email protected]) Neel Mehta ([email protected]) Why AV? Attractive Attack Surface – Gateways, Servers, Clients, ISP’s, Third Party Vendor Products – Heterogeneous and Layered Environments Why AV? –Un-trusted Data Processing • Must be reachable by external input to be useful Why AV? –Run on a variety of Platforms • Windows, Linux, Solaris, Mac How Does AV work? – Signature vs. Behavior • Pattern-matching / regex • File-format decomposition How Does AV work? – Enterprise vs. Consumer Architecture • $$$ & Manageability How Does AV work? – Common Core Components • IO filters • Format Engines How Does AV work? – Standard Features • Updates • Multi-Threat detection How Does AV work? – Common Configurations • Scan level • Scan sizes • Scan Method Code Coverage - Signatures – Field Values • Max Len (eg. ARJ header len 0xa28) • Magic (eg. PECOFF – “MZ” & “PE”) – Field Sizes • PE Section Header 0x28 • Tar Object 0x200 – Strings • PECOFF – section labels, common libraries – Ida Examples • LHA • ARJ • UPX Code Coverage – Core Utilities – Read • Easy to spot • Closest audit point to un-trusted input • Usually wrapped & buffered • Some truncate length Code Coverage – Core Utilities – Allocation • Any calculations to length are interesting • Usually wrapped • Some check 4 zero • Some add to length for internal headers • Some wrappers will truncate length Code Coverage –Constructs – Conversions • String/Number • Byte Ordering Code Coverage –Constructs – Checksum, CRC, etc. • Easy to spot (ror, xor, etc. in a loop) • Gives un-trusted input context Code Coverage –Constructs – Inherited File Structures & Commonly Grouped Processors • Are annoying to trace, due to indirection • Can reveal more subtle unchecked copies • Ex: Is MZ -> Is PE -> Is UPX Audit Points - Inefficiencies – Engine vs. -

Answers to Exercises
Answers to Exercises A bird does not sing because he has an answer, he sings because he has a song. —Chinese Proverb Intro.1: abstemious, abstentious, adventitious, annelidous, arsenious, arterious, face- tious, sacrilegious. Intro.2: When a software house has a popular product they tend to come up with new versions. A user can update an old version to a new one, and the update usually comes as a compressed file on a floppy disk. Over time the updates get bigger and, at a certain point, an update may not fit on a single floppy. This is why good compression is important in the case of software updates. The time it takes to compress and decompress the update is unimportant since these operations are typically done just once. Recently, software makers have taken to providing updates over the Internet, but even in such cases it is important to have small files because of the download times involved. 1.1: (1) ask a question, (2) absolutely necessary, (3) advance warning, (4) boiling hot, (5) climb up, (6) close scrutiny, (7) exactly the same, (8) free gift, (9) hot water heater, (10) my personal opinion, (11) newborn baby, (12) postponed until later, (13) unexpected surprise, (14) unsolved mysteries. 1.2: A reasonable way to use them is to code the five most-common strings in the text. Because irreversible text compression is a special-purpose method, the user may know what strings are common in any particular text to be compressed. The user may specify five such strings to the encoder, and they should also be written at the start of the output stream, for the decoder’s use. -
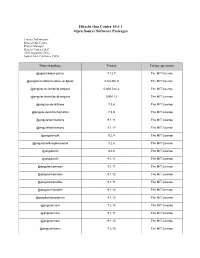
Open Source Software Packages
Hitachi Ops Center 10.5.1 Open Source Software Packages Contact Information: Hitachi Ops Center Project Manager Hitachi Vantara LLC 2535 Augustine Drive Santa Clara, California 95054 Name of package Version License agreement @agoric/babel-parser 7.12.7 The MIT License @angular-builders/custom-webpack 8.0.0-RC.0 The MIT License @angular-devkit/build-angular 0.800.0-rc.2 The MIT License @angular-devkit/build-angular 0.901.12 The MIT License @angular-devkit/core 7.3.8 The MIT License @angular-devkit/schematics 7.3.8 The MIT License @angular/animations 9.1.11 The MIT License @angular/animations 9.1.12 The MIT License @angular/cdk 9.2.4 The MIT License @angular/cdk-experimental 9.2.4 The MIT License @angular/cli 8.0.0 The MIT License @angular/cli 9.1.11 The MIT License @angular/common 9.1.11 The MIT License @angular/common 9.1.12 The MIT License @angular/compiler 9.1.11 The MIT License @angular/compiler 9.1.12 The MIT License @angular/compiler-cli 9.1.12 The MIT License @angular/core 7.2.15 The MIT License @angular/core 9.1.11 The MIT License @angular/core 9.1.12 The MIT License @angular/forms 7.2.15 The MIT License @angular/forms 9.1.0-next.3 The MIT License @angular/forms 9.1.11 The MIT License @angular/forms 9.1.12 The MIT License @angular/language-service 9.1.12 The MIT License @angular/platform-browser 7.2.15 The MIT License @angular/platform-browser 9.1.11 The MIT License @angular/platform-browser 9.1.12 The MIT License @angular/platform-browser-dynamic 7.2.15 The MIT License @angular/platform-browser-dynamic 9.1.11 The MIT License @angular/platform-browser-dynamic -

Powerbook G4 • Expo – Os
e d REVIEWED: OS 9.1, iTUNES, NEW POWER MACS i s n i Macworld o c s i MORE NEWS, MORE REVIEWS EPO!c n MARCH 2001 a r F n a S F m ul ro l details f POWERBOOK G4 • EXPO – OS X; NEW POWER MACS; OS 9.1, iTUNES, iDVD • 17/19 SCREENS PREMIERE 6.0 Macworldwww.macworld.co.uk Sex power& Inside Apple’s Titanium PowerBook G4 Get personal 20 ways to customize your Mac 17-19-inch screens We test the best mid-size monitors Mac OS X refined Adobe Premiere 6.0 Reviewed and rated read me first Simon Jary Are you ready to trust the Mac as editor-in-chief the very centre of your existence? Steve’s digital hub test n January, Apple CEO Steve Jobs electrified the 6 You think Bill Gates is… Macworld Expo crowds with his vision of the “third (a) The devil himself, who robbed our Apple of its innovative great age of the personal computer”. This new era graphical user interface to create the evil Windows empire; I is based around the convergence of digital devices (b) A bit dodgy in his business dealings, but also – cameras, PDAs, mobile phones, e-books, camcorders the man who bought us Office 2001 on the Mac; … and, probably, those smart-fridges that we’re always (c) The former bass player in the Rolling Stones. being told will control our lives in the next couple of 7 It’s bedtime. You’ve poured yourself a Horlicks, and are years, but still allow milk to go rancid a few days after ready to settle down with a good book. -

Software Requirements Specification
Software Requirements Specification for PeaZip Requirements for version 2.7.1 Prepared by Liles Athanasios-Alexandros Software Engineering , AUTH 12/19/2009 Software Requirements Specification for PeaZip Page ii Table of Contents Table of Contents.......................................................................................................... ii 1. Introduction.............................................................................................................. 1 1.1 Purpose ........................................................................................................................1 1.2 Document Conventions.................................................................................................1 1.3 Intended Audience and Reading Suggestions...............................................................1 1.4 Project Scope ...............................................................................................................1 1.5 References ...................................................................................................................2 2. Overall Description .................................................................................................. 3 2.1 Product Perspective......................................................................................................3 2.2 Product Features ..........................................................................................................4 2.3 User Classes and Characteristics .................................................................................5 -

Sophos Endpoint Security Versus Cylance Cylanceprotect Comparative Analysis 2016 June
Sophos Endpoint Security Versus Cylance CylancePROTECT Comparative Analysis 2016 June Table of Contents 1 Introduction .................................................................................................................................................................................... 3 1.1 Sophos Endpoint Security and Control ........................................................................................................................ 3 1.2 Cylance CylancePROTECT .............................................................................................................................................. 3 1.3 Executive Summary ............................................................................................................................................................ 3 2 Tests Employed .............................................................................................................................................................................. 4 2.1 High-Level Overview of the Tests ................................................................................................................................. 4 2.2 In-the-Wild Malware Real Time Protection Test ....................................................................................................... 4 2.3 False Positive Test .............................................................................................................................................................. 7 2.3.1 False Positive Test – Packer Test