Characterization of Catastrophic Instabilities: Market Crashes As Paradigm
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

1332 Nippon Suisan Kaisha, Ltd. 50 1333 Maruha Nichiro Corp. 500 1605 Inpex Corp
Nikkei Stock Average - Par Value (Update:August/1, 2017) Code Company Name Par Value(Yen) 1332 Nippon Suisan Kaisha, Ltd. 50 1333 Maruha Nichiro Corp. 500 1605 Inpex Corp. 125 1721 Comsys Holdings Corp. 50 1801 Taisei Corp. 50 1802 Obayashi Corp. 50 1803 Shimizu Corp. 50 1808 Haseko Corp. 250 1812 Kajima Corp. 50 1925 Daiwa House Industry Co., Ltd. 50 1928 Sekisui House, Ltd. 50 1963 JGC Corp. 50 2002 Nisshin Seifun Group Inc. 50 2269 Meiji Holdings Co., Ltd. 250 2282 Nh Foods Ltd. 50 2432 DeNA Co., Ltd. 500/3 2501 Sapporo Holdings Ltd. 250 2502 Asahi Group Holdings, Ltd. 50 2503 Kirin Holdings Co., Ltd. 50 2531 Takara Holdings Inc. 50 2768 Sojitz Corp. 500 2801 Kikkoman Corp. 50 2802 Ajinomoto Co., Inc. 50 2871 Nichirei Corp. 100 2914 Japan Tobacco Inc. 50 3086 J.Front Retailing Co., Ltd. 100 3099 Isetan Mitsukoshi Holdings Ltd. 50 3101 Toyobo Co., Ltd. 50 3103 Unitika Ltd. 50 3105 Nisshinbo Holdings Inc. 50 3289 Tokyu Fudosan Holdings Corp. 50 3382 Seven & i Holdings Co., Ltd. 50 3401 Teijin Ltd. 250 3402 Toray Industries, Inc. 50 3405 Kuraray Co., Ltd. 50 3407 Asahi Kasei Corp. 50 3436 SUMCO Corp. 500 3861 Oji Holdings Corp. 50 3863 Nippon Paper Industries Co., Ltd. 500 3865 Hokuetsu Kishu Paper Co., Ltd. 50 4004 Showa Denko K.K. 500 4005 Sumitomo Chemical Co., Ltd. 50 4021 Nissan Chemical Industries, Ltd. 50 4042 Tosoh Corp. 50 4043 Tokuyama Corp. 50 WF-101-E-20170803 Copyright © Nikkei Inc. All rights reserved. 1/5 Nikkei Stock Average - Par Value (Update:August/1, 2017) Code Company Name Par Value(Yen) 4061 Denka Co., Ltd. -

Consolidated Financial Statements Toho Zinc Co., Ltd. And
Consolidated Financial Statements Toho Zinc Co., Ltd. and Consolidated Subsidiaries For the year ended March 31, 2020 with Independent Auditor’s Report Toho Zinc Co., Ltd. and Consolidated Subsidiaries Contents to Consolidated Financial Statements Independent Auditor’s Report ------------------------------------------------------------- 1 Consolidated Balance Sheet --------------------------------------------------------------- 4 Consolidated Statement of Operations --------------------------------------------------- 6 Consolidated Statement of Comprehensive Income ------------------------------------- 7 Consolidated Statement of Changes in Net Assets ------------------------------------- 8 Consolidated Statement of Cash Flows -------------------------------------------------- 10 Notes to Consolidated Financial Statements -------------------------------------------- 11 Independent Auditor’s Report The Board of Directors Toho Zinc Co., Ltd. Opinion We have audited the accompanying consolidated financial statements of Toho Zinc Co., Ltd. and its subsidiaries (the Group), which comprise the consolidated balance sheet as at March 31, 2020, and the consolidated statements of income, comprehensive income, changes in net assets, and cash flows for the year then ended, and notes to the consolidated financial statements. In our opinion, the accompanying consolidated financial statements present fairly, in all material respects, the consolidated financial position of the Group as at March 31, 2020, and its consolidated financial performance and -

The Mineral Industry of Japan in 1998
THE MINERAL INDUSTRY OF JAPAN By John C. Wu Japan’s reserves of limestone, pyrophyllite, and silica are important role in supplying the ferrous and nonferrous metals, quite large. Japan has considerable reserves of coal and iodine, fabricated metal products, and industrial mineral products to but its reserves of natural gas and crude petroleum are very the construction and manufacturing industries of China, small. As a result of exploration conducted in the past 5 years including Hong Kong, Indonesia, the Republic of Korea, by the Metal Mining Agency of Japan (MMAJ), a Malaysia, Singapore, Thailand, and Taiwan. semigovernment agency under the Ministry of International For the first time since the end of World War II, the Japanese Trade and Industry (MITI), reserves of gold, lead, and zinc had economy went into a severe recession in 1998 after 5 years of been extended (Metal Mining Agency of Japan, 1998a), but slow growth in the 1990’s. According to the Economic Japan’s reserves of ferrous and nonferrous minerals are small. Planning Agency and MITI, Japan’s economy, as measured by Japan relied on imports to meet more than 95% of its raw GDP in 1990 constant yen, contracted 2.8% in 1998. material requirements for energy, ferrous metals, and Restructuring in the financial, manufacturing, and other sectors nonferrous metals for its mineral-processing and mineral- had resulted in a substantial increase in unemployment, which related manufacturing sectors. Japan also relied on imports to reached a record rate of 4.1% in 1998. The depressed real meet between 10% and 25% of its requirements for refined estate and stock markets had caused the major banks to carry a nonferrous metal products, industrial mineral products, and heavy load of bad loans, with limited funds available for refined petroleum products. -

The Mining Industry of Japan Is Made up of a Small Non-Ferrous Metal Mining Sector and a Large World-Class Minerals Processing Sector
TheThe MiningMining IndustryIndustry ofof JapanJapan METAL MINING AGENCY OF JAPAN Mineral Resources Information Center 34 MT Bldg., 1-25-5 Toranomon, Minato-ku, Tokyo JAPAN 105-0001 Tel: (81) 3 5512 1418 Fax: (81) 3 3593 9410 E-mail: [email protected] Contents Overview 1 Supply & demand of non-ferrous metals 2 Major metal smelters & refineries 12 Major metal mines 14 Major metal prices/stocks 15 Key sector contacts 16 Mineral Resources Information Center (MRIC) The Mineral Resources Information Center (MRIC) was established as a department of the Metal Mining Agency of Japan (MMAJ) in 1968. The MRIC collects, distributes and analyzes information related to nonferrous metal resources exploration and development in both Japan and around the world, on topics such as developments in the world mining industry, geological data, supply & demand statistics, mining law and mineral investment. This information is made publicly available in reports and on the Internet. The MRIC also organizes conferences and seminars on mining-related issues, and administers the MMAJ’s 10 Overseas Offices. For further information on the MRIC and its various publications, please access the MMAJ’s Internet homepage at: http://www.mmaj.go.jp Cover Photo: A gold-silver bearing quartz vein at the Hishikari Mine (courtesy of Sumitomo Metal Mining) Published in December 2002 TheThe MiningMining IndustryIndustry ofof JapanJapan Overview The mining industry of Japan is made up of a small non-ferrous metal mining sector and a large world-class minerals processing sector. In 1970 there were 246 operating metal mines employing 34,000 people. In June 2001 Kamioka mine (Pb,Zn) was closed, so the above number has dwindled to 14 operating mines, among which the most significant ones are Toyoha (Pb,Zn) and Hishikari (Au,Ag), employing about 400 people in total. -

Contact List of Environmental Business
Contact List of Environmental Business 2020/9 Company Name Window Department Location URL TEL FAX SUMITOMO METAL MINING NON-FERROUS METALS Shimbashi Sumitomo Building 11-3, Shimbashi 5-chome, Minato-ku Tokyo http://www.smm.co.jp 81-3-3436-7891 81-3-3436-7783 CO.,LTD. DIVISION 105-8716 Japan Chugaikogyo Building CHUGAIMINING CO.,LTD Precious Metal section ueno5-chome,taitou-ku http://www.chugaikogyo.co.jp 81-3-3837-3804 81-3-3837-3809 Tokyo 110-0005 Japan ENVIRONMENT・ 1-8-2,MARUNOUCHI TOHO ZINC Co.,Ltd RECYCLING CHIYODA-KU,TOKYO http://www.toho-zinc.co.jp 81-3-6212-1708 81-3-3284-1523 BUSINESS DIVISION 100-8207,JAPAN DOWA Eco-System Co.,Ltd. 4-14-1,Sotokanda,Chiyoda-ku,Tokyo DOWA Holdings Co.,Ltd. 101-0021 Japan http://www.dowa-eco.co.jp 81-3-6847-1234 81-3-6847-1243 Recycling Business Unit JX Nippon Mining & Metals 10-4, Toranomon 2-chome, Minato-ku, Metals & Recycling Division Tokyo 105-8417 ,Japan http://www.nmm.jx-group.co.jp/english/ 81-3-6433-6326 81-3-5570-2171 Corporation Machinery & Environmental Yusen Building,3-2 Marunouchi 2- Nittetsu Mining Co.,Ltd. chome,Chiyoda-ku,Tokyo 100- http://www.nittetsukou.co.jp 81-3-3216-5320 81-3-3216-5262 Sales Department 8377,Japan 1-3 Nihonbashi Horidomecho 2-chome, Nomura Kohsan Co.,Ltd. Sales Dept Chuo-ku Tokyo 103-0012 Japan http://nkcl.jp/ 81-3-5695-2531 81-3-5695-2540 Furukawa Metals & 2-3, Marunouchi 2-chome, Chiyoda-ku, FURUKAWA CO.,LTD. Resources Co., Ltd. -

STOXX Japan 600 Last Updated: 03.04.2018
STOXX Japan 600 Last Updated: 03.04.2018 Rank Rank (PREVIOUS ISIN Sedol RIC Int.Key Company Name Country Currency Component FF Mcap (BEUR) (FINAL) ) JP3633400001 6900643 7203.T 690064 Toyota Motor Corp. JP JPY Large 140.9 1 1 JP3902900004 6335171 8306.T 659668 Mitsubishi UFJ Financial Group JP JPY Large 69.7 2 2 JP3436100006 6770620 9984.T 677062 Softbank Group Corp. JP JPY Large 52.8 3 3 JP3854600008 6435145 7267.T 643514 Honda Motor Co. Ltd. JP JPY Large 50.7 4 5 JP3435000009 6821506 6758.T 682150 Sony Corp. JP JPY Large 49.8 5 6 JP3735400008 6641373 9432.T 664137 Nippon Telegraph & Telephone C JP JPY Large 48.7 6 4 JP3890350006 6563024 8316.T 656302 Sumitomo Mitsui Financial Grou JP JPY Large 48.2 7 7 JP3236200006 6490995 6861.T 649099 Keyence Corp. JP JPY Large 47.4 8 8 JP3756600007 6639550 7974.T 663955 Nintendo Co. Ltd. JP JPY Large 43.0 9 9 JP3802400006 6356934 6954.T 635693 Fanuc Ltd. JP JPY Large 40.0 10 10 JP3496400007 6248990 9433.T 624899 KDDI Corp. JP JPY Large 37.2 11 13 JP3885780001 6591014 8411.T 625024 Mizuho Financial Group Inc. JP JPY Large 37.2 12 11 JP3898400001 6596785 8058.T 659678 Mitsubishi Corp. JP JPY Large 34.8 13 12 JP3371200001 6804585 4063.T 680458 Shin-Etsu Chemical Co. Ltd. JP JPY Large 34.5 14 15 JP3734800000 6640682 6594.T 664068 Nidec Corp. JP JPY Large 34.3 15 14 JP3970300004 BQRRZ00 6098.T JP503G RECRUIT HOLDINGS JP JPY Large 32.0 16 20 JP3242800005 6172323 7751.T 617232 Canon Inc. -

First Edition
dfd Monday, 13 May 2013 (First Edition) Japan Daily Featured stocks Top of the Pack Price TP Upside Nissan Motor (7201) OUTPERFORM TP ¥1,150 Takahashi Rating 10 May TP FY3/13 results: when will "surplus" cash be returned to shareholders? Results Panasonic 6752 Corporation O 749 750 0.1% FOCUS LIST STOCK Square Enix Sumitomo Electric Industries (5802) OUTPERFORM TP ¥1,500 Okumoto/ Yamada 9684 Holdings O 1240 1450 16.9% Potential OP upside of ¥50bn; margin deterioration unlikely amid rising production Results 6501 Hitachi N 645 510 -20.9% FOCUS LIST STOCK Dainippon Screen 7735 Mfg. N 536 510 -4.9% Square Enix Holdings (9684) Neutral->OUTPERFORM TP ¥1,150->¥1,450 Tsuchiya Nippon Telegraph Announcement of additional structural reforms should mark the end of bad news Upgrade Rating 9432 and Telephone O 5080 4700 -7.5% Yakult Honsha (2267) Underperform-> NEUTRAL TP ¥2,700->¥4,100 Kawasaki/Yamate Konica Minolta Upgrade to NEUTRAL; Positive on better cost awareness Upgrade Rating 4902 Holdings N 759 650 -14.4% 3659 NEXON O 1192 1300 9.1% Technology 6640 Dai-ichi Seiko N 1548 1300 -16.0% Panasonic Corporation (6752) OUTPERFORM TP ¥750 Tsuchiya 7915 Nissha Printing N 2186 1660 -24.1% Prospects for bringing forward restructuring positive Results 7201 Nissan Motor Co. O 1063 1150 8.2% Square Enix Holdings (9684) Neutral->OUTPERFORM TP ¥1,150->¥1,450 Tsuchiya 6141 Mori Seiki U 1267 900 -29.0% Announcement of additional structural reforms should mark the end of bad news Upgrade Rating 6471 NSK O 873 800 -8.4% 6326 Kubota U 1434 1150 -19.8% Hitachi (6501) NEUTRAL TP ¥510 Maekawa/ Fukumoto 6268 Nabtesco Corp N 2457 1650 -32.8% Little prospect of organic growth, Smart Transformation-driven profit expansion Results 2229 Calbee N 9490 7300 -23.1% Dainippon Screen Mfg. -
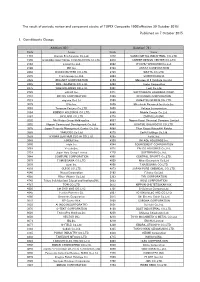
Published on 7 October 2015 1. Constituents Change the Result Of
The result of periodic review and component stocks of TOPIX Composite 1500(effective 30 October 2015) Published on 7 October 2015 1. Constituents Change Addition( 80 ) Deletion( 72 ) Code Issue Code Issue 1712 Daiseki Eco.Solution Co.,Ltd. 1972 SANKO METAL INDUSTRIAL CO.,LTD. 1930 HOKURIKU ELECTRICAL CONSTRUCTION CO.,LTD. 2410 CAREER DESIGN CENTER CO.,LTD. 2183 Linical Co.,Ltd. 2692 ITOCHU-SHOKUHIN Co.,Ltd. 2198 IKK Inc. 2733 ARATA CORPORATION 2266 ROKKO BUTTER CO.,LTD. 2735 WATTS CO.,LTD. 2372 I'rom Group Co.,Ltd. 3004 SHINYEI KAISHA 2428 WELLNET CORPORATION 3159 Maruzen CHI Holdings Co.,Ltd. 2445 SRG TAKAMIYA CO.,LTD. 3204 Toabo Corporation 2475 WDB HOLDINGS CO.,LTD. 3361 Toell Co.,Ltd. 2729 JALUX Inc. 3371 SOFTCREATE HOLDINGS CORP. 2767 FIELDS CORPORATION 3396 FELISSIMO CORPORATION 2931 euglena Co.,Ltd. 3580 KOMATSU SEIREN CO.,LTD. 3079 DVx Inc. 3636 Mitsubishi Research Institute,Inc. 3093 Treasure Factory Co.,LTD. 3639 Voltage Incorporation 3194 KIRINDO HOLDINGS CO.,LTD. 3669 Mobile Create Co.,Ltd. 3197 SKYLARK CO.,LTD 3770 ZAPPALLAS,INC. 3232 Mie Kotsu Group Holdings,Inc. 4007 Nippon Kasei Chemical Company Limited 3252 Nippon Commercial Development Co.,Ltd. 4097 KOATSU GAS KOGYO CO.,LTD. 3276 Japan Property Management Center Co.,Ltd. 4098 Titan Kogyo Kabushiki Kaisha 3385 YAKUODO.Co.,Ltd. 4275 Carlit Holdings Co.,Ltd. 3553 KYOWA LEATHER CLOTH CO.,LTD. 4295 Faith, Inc. 3649 FINDEX Inc. 4326 INTAGE HOLDINGS Inc. 3660 istyle Inc. 4344 SOURCENEXT CORPORATION 3681 V-cube,Inc. 4671 FALCO HOLDINGS Co.,Ltd. 3751 Japan Asia Group Limited 4779 SOFTBRAIN Co.,Ltd. 3844 COMTURE CORPORATION 4801 CENTRAL SPORTS Co.,LTD. -

Mizuho BK Custody and Proxy Board Lot Size List JUN 22 , 2021
Mizuho BK Custody and Proxy Board Lot Size List JUN 22 , 2021 Board Lot Stock Name (in Alphabetical Order) ISIN Code QUICK Code Size 21LADY CO.,LTD. 100 JP3560550000 3346 3-D MATRIX,LTD. 100 JP3410730000 7777 4CS HOLDINGS CO.,LTD. 100 JP3163300001 3726 A-ONE SEIMITSU INC. 100 JP3160660001 6156 A.D.WORKS GROUP CO.,LTD. 100 JP3160560003 2982 A&A MATERIAL CORPORATION 100 JP3119800005 5391 A&D COMPANY,LIMITED 100 JP3160130005 7745 ABALANCE CORPORATION 100 JP3969530009 3856 ABC-MART,INC. 100 JP3152740001 2670 ABHOTEL CO.,LTD. 100 JP3160610006 6565 ABIST CO.,LTD. 100 JP3122480001 6087 ACCESS CO.,LTD. 100 JP3108060009 4813 ACCESS GROUP HOLDINGS CO.,LTD. 100 JP3108190004 7042 ACCRETE INC. 100 JP3108180005 4395 ACHILLES CORPORATION 100 JP3108000005 5142 ACMOS INC. 100 JP3108100003 6888 ACOM CO.,LTD. 100 JP3108600002 8572 ACRODEA,INC. 100 JP3108120001 3823 ACTIVIA PROPERTIES INC. 1 JP3047490002 3279 AD-SOL NISSIN CORPORATION 100 JP3122030004 3837 ADASTRIA CO.,LTD. 100 JP3856000009 2685 ADEKA CORPORATION 100 JP3114800000 4401 ADISH CO.,LTD. 100 JP3121500007 7093 ADJUVANT COSME JAPAN CO.,LTD. 100 JP3119620007 4929 ADTEC PLASMA TECHNOLOGY CO.,LTD. 100 JP3122010006 6668 ADVAN CO.,LTD. 100 JP3121950004 7463 ADVANCE CREATE CO.,LTD. 100 JP3122100005 8798 ADVANCE RESIDENCE INVESTMENT CORPORATION 1 JP3047160001 3269 ADVANCED MEDIA,INC. 100 JP3122150000 3773 ADVANEX INC. 100 JP3213400009 5998 ADVANTAGE RISK MANAGEMENT CO.,LTD. 100 JP3122410008 8769 ADVANTEST CORPORATION 100 JP3122400009 6857 ADVENTURE,INC. 100 JP3122380003 6030 ADWAYS INC. 100 JP3121970002 2489 AEON CO.,LTD. 100 JP3388200002 8267 AEON DELIGHT CO.,LTD. 100 JP3389700000 9787 AEON FANTASY CO.,LTD. 100 JP3131420006 4343 AEON FINANCIAL SERVICE CO.,LTD. -
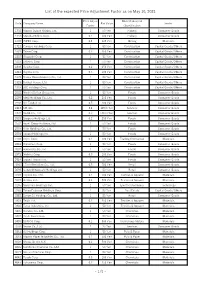
List of the Expected Price Adjustment Factor As on May 10, 2021
List of the expected Price Adjustment Factor as on May 10, 2021 Price Adjust Nikkei Industrial Code Company Name Par Value Sector Factor Classification 1332 Nippon Suisan Kaisha, Ltd. 1 50 Yen Fishery Consumer Goods 1333 Maruha Nichiro Corp. 0.1 500 Yen Fishery Consumer Goods 1605 INPEX Corp. 0.4 125 Yen Mining Materials 1721 Comsys Holdings Corp. 1 50 Yen Construction Capital Goods/Others 1801 Taisei Corp. 0.2 250 Yen Construction Capital Goods/Others 1802 Obayashi Corp. 1 50 Yen Construction Capital Goods/Others 1803 Shimizu Corp. 1 50 Yen Construction Capital Goods/Others 1808 Haseko Corp. 0.2 250 Yen Construction Capital Goods/Others 1812 Kajima Corp. 0.5 100 Yen Construction Capital Goods/Others 1925 Daiwa House Industry Co., Ltd. 1 50 Yen Construction Capital Goods/Others 1928 Sekisui House, Ltd. 1 50 Yen Construction Capital Goods/Others 1963 JGC Holdings Corp. 1 50 Yen Construction Capital Goods/Others 2002 Nisshin Seifun Group Inc. 1 50 Yen Foods Consumer Goods 2269 Meiji Holdings Co., Ltd. 0.2 250 Yen Foods Consumer Goods 2282 NH Foods Ltd. 0.5 100 Yen Foods Consumer Goods 2413 M3, Inc. 2.4 125/6 Yen Services Consumer Goods 2432 DeNA Co., Ltd. 0.3 500/3 Yen Services Consumer Goods 2501 Sapporo Holdings Ltd. 0.2 250 Yen Foods Consumer Goods 2502 Asahi Group Holdings, Ltd. 1 50 Yen Foods Consumer Goods 2503 Kirin Holdings Co., Ltd. 1 50 Yen Foods Consumer Goods 2531 Takara Holdings Inc. 1 50 Yen Foods Consumer Goods 2768 Sojitz Corp. 0.1 500 Yen Trading Companies Materials 2801 Kikkoman Corp. -

Notice of the 120Th Ordinary General Meeting of Shareholders
Note: This document has been translated from a part of the Japanese original for reference purposes only. In the event of any discrepancy between this translated document and the Japanese original, the original shall prevail. Securities identification code: 5707 June 5, 2019 To our shareholders: Kimiyasu Marusaki Representative Director and President Toho Zinc Co., Ltd. 1-8-2 Marunouchi, Chiyoda-ku, Tokyo NOTICE OF THE 120TH ORDINARY GENERAL MEETING OF SHAREHOLDERS You are cordially invited to attend the 120th Ordinary General Meeting of Shareholders of Toho Zinc Co., Ltd. (the “Company”), which will be held as described below. If you are unable to attend the meeting in person, you may exercise your voting rights by either of the methods below. Please exercise your voting rights after reviewing the Reference Documents for the General Meeting of Shareholders hereafter. [Voting in Writing] Please indicate your approval or disapproval of the proposals on the enclosed voting form and return it by postal mail to reach us no later than 5:40 p.m., Wednesday, June 26, 2019 (Japan Standard Time). [Voting via the Internet] Please access the voting website designated by the Company (https://evote.tr.mufg.jp/), use the login ID and temporary password written on the enclosed voting form, and then indicate your approval or disapproval of the proposals by following the instructions on the screen by no later than 5:40 p.m., Wednesday, June 26, 2019 (Japan Standard Time). Please also confirm “Instructions for exercising voting rights via the Internet” when voting via the Internet. (This only applies to those who received the Japanese version of this Notice) 1. -

Download the Full GTC ONE Minute Brief
Equity | Currencies & Commodities | Corporate & Global Economic News | Economic Calendar 14 December 2016 Economic and Political News Key Indices Ratings agency, Fitch, has retained its negative outlook on South African 1 Day 1 D % WTD % MTD % Prev. Month YTD % utilities, considering the slow economic growth and moderate electricity Last Close Chg Chg Chg Chg % Chg Chg demand in 2017. JSE All Share 50839.25 311.39 0.62% -0.12% 1.25% -0.75% 0.29% The International Monetary Fund indicated that the key factors that are expected to affect South Africa’s economic growth next year would be JSE Top 40 44170.66 278.15 0.63% -0.11% 1.10% -0.75% -3.55% uncertainty regarding policy direction and perceptions of weakening governance. FTSE 100 6968.57 78.15 1.13% 0.21% 2.72% -2.45% 11.63% The Department of Energy stated that Eskom will be the procurement DAX 30 11284.65 94.44 0.84% 0.72% 6.06% -0.23% 5.04% agency for the planned nuclear program in the country. Further, Eskom’s Acting Chief Executive Officer, Matshela Koko, announced that the CAC 40 4803.87 43.10 0.91% 0.84% 4.93% 1.53% 3.60% power utility group will invite bids to build six nuclear reactors in the S&P 500 2271.72 14.76 0.65% 0.54% 3.32% 3.42% 11.14% Government’s push to expand South Africa’s nuclear capacity. Nasdaq 5463.83 51.29 0.95% 0.36% 2.63% 2.59% 9.11% The Treasury announced that its Chief Procurement Officer, Kenneth Composite Brown, will leave at the end of December.