Unsupervised Modeling of the Movement of Basketball Players Using a Deep Generative Model
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Charlotte Bobcats
__________________________________________________________________________ __________________________________________________________________________ ALEX STEFANESCU TABLE OF CONTENTS • Awards & Certificates o SIFE Service Leadership Award o PRSSA Certificate of Membership • Charlotte Bobcats o News releases o Other items • CarolinaNightlife.com o News releases o Blog entries • Student Niner Media o Articles & Blog entries • Miscellaneous Items o SIFE Recruitment Flyer AWARDS & CERTIFICATES BOBCATS SPORTS & ENTERTAINMENT, MOBILITIE ANNOUNCE PARTNERSHIP December 21, 2011 – Bobcats Sports & Entertainment President & COO Fred Whitfield announced today the organization has started a partnership with telecommunications infrastructure company, Mobilitie. “We are delighted about our new partnership with Mobilitie,” said Whitfield. “We continually strive to make the fan experience at Time Warner Cable Arena the best in the business and Mobilitie will help us achieve that.” Under the terms of the partnership Mobilitie will provide Distributed Antenna Systems (DAS) that will enhance cellular coverage inside Time Warner Cable Arena. Visitors will have stronger signal, better cell phone reception and fewer dropped calls. The distributed architecture of indoor DAS ensures that customers get wireless coverage inside buildings, in underground train stations and in all other types of indoor environments that traditionally have poor wireless coverage. About Mobilitie: Mobilitie vision is to be the premier owner/investor and lessor of capital assets to -

Cleveland Moves Step Closer to NBA Finals Cavs Rip Raptors for 10Th Playoff Win in a Row
Mocked Martial becomes Man Utd’s FA Cup charm SATURDAY, MAY 21, 2016 MAY SATURDAY, SportsSports 46 CLEVELAND: Cleveland Cavaliers’ Kyrie Irving, right, shoots against Toronto Raptors’ Bismack Biyombo (8) during the first half fo Game 2 of the NBA basketball Eastern Conference finals. — AP Cleveland moves step closer to NBA finals Cavs rip Raptors for 10th playoff win in a row WASHINGTON: With LeBron James producing rhythm I can do other things to help us win.” Lethal LeBron Cavs sparked another overpowering performance, the “This is the best I’ve felt in a while. When you The playoff victory was Cleveland’s 17th in The Cavaliers closed the second quarter Cleveland Cavaliers routed Toronto 108-89 have two guys like this to help you, it takes a a row over foes from the same conference, with a 16-2 run to seize a 62-48 half-time edge. Thursday, stretching their playoff record to 10- lot of things off you.” The Cavaliers are two the longest such NBA streak since 1970-71. “I “We made some adjustments, changed our 0 and moving closer to an NBA Finals return. wins from facing the Western Conference don’t think it feels like a streak,” James said. defense, got a little more physical that was a James scored 23 points, grabbed 11 champion, either Oklahoma City or defending “We won one game. How do we get better big spark,” Lue said of that stretch. James had rebounds and passed out 11 assists as the host NBA champion Golden State, in the NBA Finals the next game? We haven’t overlooked any 17 points, eight assists and seven rebounds in Cavaliers, who swept through the first two that begin on June 2. -

National Basketball Association Official
NATIONAL BASKETBALL ASSOCIATION OFFICIAL SCORER'S REPORT FINAL BOX 3/31/2014 Time Warner Cable Arena, Charlotte, NC Officials: #17 Joe Crawford, #20 Leroy Richardson, #52 Scott Twardoski Time of Game: 2:07 Attendance: 14,894 VISITOR: Washington Wizards (38-36) NO PLAYER MIN FG FGA 3P 3PA FT FTA OR DR TOT A PF ST TO BS PTS 1 Trevor Ariza F 29:55 4 9 3 5 0 0 0 2 2 1 1 0 1 0 11 35 Trevor Booker F 19:48 2 5 0 0 0 0 1 1 2 1 1 2 0 1 4 4 Marcin Gortat C 26:56 3 7 0 0 0 0 2 9 11 1 3 0 1 1 6 3 Bradley Beal G 39:52 8 12 2 3 2 3 0 2 2 5 3 0 4 1 20 2 John Wall G 29:16 4 16 0 1 2 3 0 1 1 6 2 0 5 0 10 90 Drew Gooden 27:13 5 12 0 2 2 2 4 4 8 2 5 2 0 0 12 9 Martell Webster 26:40 5 7 2 3 2 2 0 2 2 1 2 0 1 0 14 7 Al Harrington 20:38 4 5 2 3 1 3 0 5 5 0 3 1 1 0 11 24 Andre Miller 18:44 2 5 0 0 0 0 1 2 3 9 1 1 1 0 4 13 Kevin Seraphin 0:59 1 1 0 0 0 0 1 0 1 0 0 0 0 0 2 22 Otto Porter DNP - Coach's Decision 31 Chris Singleton DNP - Coach's Decision 17 Garrett Temple DNP - Coach's Decision TOTALS: 38 79 9 17 9 13 9 28 37 26 21 6 14 3 94 PERCENTAGES: 48.1% 52.9% 69.2% TM REB: 4 TOT TO: 15 (17 PTS) HOME: CHARLOTTE BOBCATS (36-38) NO PLAYER MIN FG FGA 3P 3PA FT FTA OR DR TOT A PF ST TO BS PTS 14 Michael Kidd-Gilchrist F 20:50 0 5 0 0 3 4 3 3 6 0 2 1 1 0 3 11 Josh McRoberts F 27:13 1 2 0 1 0 0 3 2 5 1 1 0 0 1 2 25 Al Jefferson C 40:03 8 19 0 0 3 3 3 8 11 0 3 0 0 2 19 9 Gerald Henderson G 27:05 3 7 0 1 3 4 0 3 3 2 2 1 1 0 9 15 Kemba Walker G 38:12 6 22 0 10 9 10 1 4 5 10 2 1 1 1 21 40 Cody Zeller 20:20 4 4 0 0 7 8 3 5 8 2 1 1 1 0 15 0 Bismack Biyombo 7:57 2 2 0 0 -

Box Score Hornets
NATIONAL BASKETBALL ASSOCIATION OFFICIAL SCORER'S REPORT FINAL BOX Monday, March 1, 2021 Moda Center, Portland, OR Officials: #56 Mark Ayotte, #63 Derek Richardson, #53 John Butler Game Duration: 1:59 Attendance: Not Yet Counted VISITOR: Charlotte Hornets (16-18) POS MIN FG FGA 3P 3PA FT FTA OR DR TOT A PF ST TO BS +/- PTS 11 Cody Martin F 26:50 4 9 0 2 0 0 4 5 9 2 1 2 1 0 1 8 25 P.J. Washington F 30:02 1 8 0 1 1 2 0 3 3 2 0 0 4 1 -21 3 8 Bismack Biyombo C 28:52 3 4 0 0 0 2 2 3 5 3 1 0 0 1 4 6 3 Terry Rozier G 35:14 8 17 3 9 1 1 1 1 2 6 2 4 3 0 -8 20 2 LaMelo Ball G 32:01 10 18 5 7 5 6 2 4 6 8 3 4 3 1 -18 30 0 Miles Bridges 28:17 4 8 0 1 1 1 1 1 2 2 3 1 2 1 -2 9 1 Malik Monk 26:56 7 13 3 7 2 4 0 2 2 2 4 0 2 0 0 19 10 Caleb Martin 22:59 4 8 3 5 0 1 0 5 5 0 1 1 1 0 -11 11 6 Jalen McDaniels 08:49 2 3 1 2 0 0 1 2 3 0 1 0 0 1 -5 5 4 Devonte' Graham DNP - Injury/Illness - Left Knee; Patella Femoral Discomfort 20 Gordon Hayward DNP - Injury/Illness - Right Hand; Contusion 40 Cody Zeller DNP - Injury/Illness - Left Hip; Contusion 240:00 43 88 15 34 10 17 11 26 37 25 16 12 16 5 -12 111 48.9% 44.1% 58.8% TM REB: 10 TOT TO: 16 (28 PTS) HOME: PORTLAND TRAIL BLAZERS (19-14) POS MIN FG FGA 3P 3PA FT FTA OR DR TOT A PF ST TO BS +/- PTS 55 Derrick Jones Jr. -
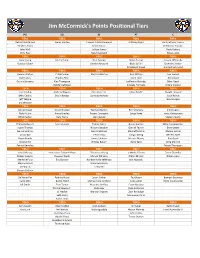
Jim Mccormick's Points Positional Tiers
Jim McCormick's Points Positional Tiers PG SG SF PF C TIER 1 TIER 1 TIER 1 TIER 1 TIER 1 Russell Westbrook James Harden Giannis Antetokounmpo Anthony Davis Karl-Anthony Towns Stephen Curry Kevin Durant DeMarcus Cousins John Wall LeBron James Rudy Gobert Chris Paul Kawhi Leonard Nikola Jokic TIER 2 TIER 2 TIER 2 TIER 2 TIER 2 Kyrie Irving Jimmy Butler Paul George Myles Turner Hassan Whiteside Damian Lillard Gordon Hayward Blake Griffin DeAndre Jordan Draymond Green Andre Drummond TIER 3 TIER 3 TIER 3 TIER 3 TIER 3 Kemba Walker CJ McCollum Khris Middleton Paul Millsap Joel Embiid Kyle Lowry Bradley Beal Kevin Love Al Horford Dennis Schroder Klay Thompson LaMarcus Aldridge Marc Gasol DeMar DeRozan Kirstaps Porzingis Nikola Vucevic TIER 4 TIER 4 TIER 4 TIER 4 TIER 4 Jrue Holiday Andrew Wiggins Otto Porter Jr. Julius Randle Dwight Howard Mike Conley Devin Booker Carmelo Anthony Jusuf Nurkic Jeff Teague Brook Lopez Eric Bledsoe TIER 5 TIER 5 TIER 5 TIER 5 TIER 5 Goran Dragic Victor Oladipo Harrison Barnes Ben Simmons Clint Capela Ricky Rubio Avery Bradley Robert Covington Serge Ibaka Jonas Valanciunas Elfrid Payton Gary Harris Jae Crowder Steven Adams TIER 6 TIER 6 TIER 6 TIER 6 TIER 6 D'Angelo Russell Evan Fournier Tobias Harris Aaron Gordon Willy Hernangomez Isaiah Thomas Wilson Chandler Derrick Favors Enes Kanter Dennis Smith Jr. Danilo Gallinari Markieff Morris Marcin Gortat Lonzo Ball Trevor Ariza Gorgui Dieng Nerlens Noel Rajon Rondo James Johnson Marcus Morris Pau Gasol George Hill Nicolas Batum Dario Saric Greg Monroe Patrick Beverley -

2011-12 Limited Rookie Only Checklist
2011-12 Limited Rookie Only Checklist Player Set Team Player Set Team JaJuan Johnson 2011 RC AUTO Boston Celtics Derrick Williams 2011 RC AUTO Minnesota Timberwolves MarShon Brooks 2011 RC AUTO Brooklyn Nets Gustavo Ayon 2011 RC AUTO New Orleans Hornets Kemba Walker 2011 RC AUTO Charlotte Bobcats Anthony Davis 2012 XRC New Orleans Hornets Bismack Biyombo 2011 RC AUTO Charlotte Bobcats Austin Rivers 2012 XRC New Orleans Hornets Michael Kidd-Gilchrist 2012 XRC Charlotte Bobcats Josh Harrellson 2011 RC AUTO New York Knicks Jimmy Butler 2011 RC AUTO Chicago Bulls Iman Shumpert 2011 RC AUTO New York Knicks Kyrie Irving 2011 RC AUTO Cleveland Cavaliers Reggie Jackson 2011 RC AUTO Oklahoma City Thunder Tristan Thompson 2011 RC AUTO Cleveland Cavaliers Justin Harper 2011 RC AUTO Orlando Magic Dion Waiters 2012 XRC Cleveland Cavaliers Andrew Nicholson 2012 XRC Orlando Magic Tyler Zeller 2012 XRC Cleveland Cavaliers Mo Harkless 2012 XRC Orlando Magic Kenneth Faried 2011 RC AUTO Denver Nuggets Lavoy Allen 2011 RC AUTO Philadelphia 76ers Jordan Hamilton 2011 RC AUTO Denver Nuggets Markieff Morris 2011 RC AUTO Phoenix Suns Evan Fournier 2012 XRC Denver Nuggets Kendall Marshall 2012 XRC Phoenix Suns Brandon Knight 2011 RC AUTO Detroit Pistons Nolan Smith 2011 RC AUTO Portland Trail Blazers Andre Drummond 2012 XRC Detroit Pistons Damian Lillard 2012 XRC Portland Trail Blazers Klay Thompson 2011 RC AUTO Golden State Warriors Meyers Leonard 2012 XRC Portland Trail Blazers Jeremy Tyler 2011 RC AUTO Golden State Warriors Isaiah Thomas 2011 RC AUTO Sacramento -

2020 Avg Fantasy Basketball Draft Position
RealTime Fantasy Sports 2021 Avg Fantasy Basketball Draft Position Drafts through 03-Oct-2021 04-Oct-2021 09:35 AM ET 1.07 Nikola Jokic, C DEN 85.42 Jalen Green, G HOU 137.50 Khyri Thomas, G HOU 3.14 Giannis Antetokounmpo, F MIL 85.75 Evan Mobley, C CLE 138.00 Goran Dragic, G TOR 3.64 Luka Doncic, G DAL 86.00 Keldon Johnson, F SAN 138.00 Derrick Rose, G NYK 4.86 Karl-Anthony Towns, C MIN 86.25 Mike Conley, G UTA 138.50 Killian Hayes, G DET 5.57 James Harden, G BRK 87.64 Harrison Barnes, F SAC 139.67 Tyrese Maxey, G PHI 7.21 Stephen Curry, G GSW 87.83 Kevin Porter Jr., G HOU 143.00 Isaiah Roby, F OKC 8.93 Damian Lillard, G POR 88.64 Jakob Poeltl, C SAN 143.00 Brandon Clarke, F MEM 9.14 Joel Embiid, C PHI 89.58 Derrick White, G SAN 9.79 Kevin Durant, F BRK 89.82 Spencer Dinwiddie, G WSH 9.93 Nikola Vucevic, C CHI 92.45 Jalen Suggs, G ORL 10.79 Jayson Tatum, F BOS 93.55 Mikal Bridges, F PHX 12.36 Domantas Sabonis, F IND 94.50 Andre Drummond, C PHI 14.29 Bradley Beal, G WSH 94.70 Robert Covington, F POR 14.86 Russell Westbrook, G LAL 95.33 Klay Thompson, G GSW 14.93 Anthony Davis, F LAL 97.89 John Wall, G HOU 16.21 Trae Young, G ATL 98.00 James Wiseman, C GSW 16.93 Bam Adebayo, F MIA 98.40 Norman Powell, G POR 17.21 Zion Williamson, F NOR 98.60 Montrezl Harrell, F WSH 19.43 LeBron James, F LAL 98.60 Miles Bridges, F CHA 19.43 Julius Randle, F NYK 99.40 Devonte' Graham, G NOR 19.64 Rudy Gobert, C UTA 100.78 Dennis Schroder, G BOS 20.43 Paul George, F LAC 101.45 Nickeil Alexander-Walker, G NOR 23.07 Jimmy Butler, F MIA 101.91 Malik Beasley, -

Detroit Pistons Game Notes | @Pistons PR
Date Opponent W/L Score Dec. 23 at Minnesota L 101-111 Dec. 26 vs. Cleveland L 119-128(2OT) Dec. 28 at Atlanta L 120-128 Dec. 29 vs. Golden State L 106-116 Jan. 1 vs. Boston W 96 -93 Jan. 3 vs.\\ Boston L 120-122 GAME NOTES Jan. 4 at Milwaukee L 115-125 Jan. 6 at Milwaukee L 115-130 DETROIT PISTONS 2020-21 SEASON GAME NOTES Jan. 8 vs. Phoenix W 110-105(OT) Jan. 10 vs. Utah L 86 -96 Jan. 13 vs. Milwaukee L 101-110 REGULAR SEASON RECORD: 20-52 Jan. 16 at Miami W 120-100 Jan. 18 at Miami L 107-113 Jan. 20 at Atlanta L 115-123(OT) POSTSEASON: DID NOT QUALIFY Jan. 22 vs. Houston L 102-103 Jan. 23 vs. Philadelphia L 110-1 14 LAST GAME STARTERS Jan. 25 vs. Philadelphia W 119- 104 Jan. 27 at Cleveland L 107-122 POS. PLAYERS 2020-21 REGULAR SEASON AVERAGES Jan. 28 vs. L.A. Lakers W 107-92 11.5 Pts 5.2 Rebs 1.9 Asts 0.8 Stls 23.4 Min Jan. 30 at Golden State L 91-118 Feb. 2 at Utah L 105-117 #6 Hamidou Diallo LAST GAME: 15 points, five rebounds, two assists in 30 minutes vs. Feb. 5 at Phoenix L 92-109 F Ht: 6 -5 Wt: 202 Averages: MIA (5/16)…31 games with 10+ points on year. Feb. 6 at L.A. Lakers L 129-135 (2OT) Kentucky NOTE: Scored 10+ pts in 31 games, 20+ pts in four games this season, Feb. -

Utah Jazz Draft Ex-CU Buff Alec Burks
Page 1 of 2 Utah Jazz draft Ex-CU Buff Alec Burks Guard taken 12th to end up a lottery pick By Ryan Thorburn Camera Sports Writer Boulder Daily Camera Posted:06/23/2011 06:57:18 PM MDT Alec Burks doesn't need 140 characters to describe the journey. Wheels up. ... Milwaukee. ... Tired. ... Sacramento. ... Airport life. ... Charlotte. ... Dummy tired. ... Phoenix. ... Thankful for another day. These are some of the simple messages the former Colorado guard sent via Twitter to keep his followers up to date with the journey from Colorado to the NBA. After finishing the spring semester at CU in May, Burks worked out for seven different teams. The Utah Jazz, the last team Burks auditioned for, selected the 6-foot-6 shooting guard with the No. 12 pick. Hoops dream realized. "It was exciting," Burks said during a teleconference from the the Prudential Center in Newark, N.J. not long after shaking NBA commissioner David Stern's hand and posing for photos in a new three-piece suit and Jazz cap. "I'm glad they picked me." A lot of draftniks predicted Jimmer Fredette and the Jazz would make beautiful music together, but the BYU star was taken by Milwaukee at No. 10 -- the frequently forecasted landing spot for Burks -- and then traded to Sacramento. "I don't really believe in the mock drafts," Burks said. "They don't really know what's going to happen. I'm just glad to be in the lottery." Burks, who doesn't turn 20 until next month, agonized over the decision whether to remain in college or turn professional throughout a dazzling sophomore season in Boulder. -

Dynamic Player Significance (DPS): a New Comprehensive Basketball Statistic
Dynamic Player Significance (DPS): A new comprehensive basketball statistic David Hill Media Lab, Massachusetts Institute of Technology Cambridge, Massachusetts, USA [email protected] 15.071 (The Analytics Edge) Final Project May 13, 2013 Abstract Dynamic player significance is a new basketball metric designed to measure each NBA player's importance, or significance, to his franchise. This metric attempts to clearly define each player's role on the team and how it fits with the team's identity. Its key aspect is that it is influenced by the on-court identity of each franchise, which is defined as the collection of factors that contribute most to a win by a given team. These factors differ for every NBA team. Therefore, two players with completely identical stats/skillsets, but different teams, will most likely have different significance values. Alternatively, if a player is traded from one team to another, his significance will differ on the new team even if his production remains constant. Hence, dynamic player significance. Here, I have broken down the components of the model and explored three case studies that clearly show how teams’ identities deviate. Additionally, player evaluations have been explored to show tendencies in the model across multiple conditions. The proposed statistic could help inform team personnel decisions and coaching strategies, in addition to gauging player effectiveness. Motivation In the NBA, one of the most important things for any team to establish is an identity. These are the traits that define a team. Often, identity is the major factor that governs all transactions, whether the team is looking for players, hiring a coach, or filling front office positions. -

Box Score Hornets
NATIONAL BASKETBALL ASSOCIATION OFFICIAL SCORER'S REPORT FINAL BOX Sunday, February 28, 2021 Golden 1 Center, Sacramento, CA Officials: #15 Zach Zarba, #39 Tyler Ford, #7 Lauren Holtkamp Game Duration: 2:28 Attendance: Not Yet Counted VISITOR: Charlotte Hornets (16-17) POS MIN FG FGA 3P 3PA FT FTA OR DR TOT A PF ST TO BS +/- PTS 6 Jalen McDaniels F 15:10 2 6 0 2 0 0 0 2 2 0 1 0 1 2 -17 4 25 P.J. Washington F 41:32 15 22 5 8 7 7 1 7 8 2 4 2 1 2 -5 42 8 Bismack Biyombo C 19:59 2 3 0 0 2 2 3 1 4 0 3 0 1 0 -10 6 3 Terry Rozier G 30:04 2 9 1 4 3 3 0 4 4 4 1 0 5 0 -12 8 2 LaMelo Ball G 38:31 7 12 1 2 9 10 0 4 4 12 4 0 3 1 6 24 0 Miles Bridges 32:34 5 7 3 4 0 0 2 7 9 4 3 0 0 0 15 13 1 Malik Monk 31:14 8 17 0 7 5 5 0 5 5 4 3 0 2 0 20 21 11 Cody Martin 27:15 4 5 1 2 0 0 1 0 1 3 1 1 3 1 9 9 10 Caleb Martin 03:41 0 2 0 1 0 0 0 0 0 1 0 0 0 0 -1 0 4 Devonte' Graham DND - Injury/Illness - Left Knee; Patella Femoral Discomfort 20 Gordon Hayward DND - Injury/Illness - Right Hand; Contusoin 40 Cody Zeller DND - Injury/Illness - Left Hip; Contusion 240:00 45 83 11 30 26 27 7 30 37 30 20 3 16 6 1 127 54.2% 36.7% 96.3% TM REB: 10 TOT TO: 16 (7 PTS) HOME: SACRAMENTO KINGS (13-21) POS MIN FG FGA 3P 3PA FT FTA OR DR TOT A PF ST TO BS +/- PTS 40 Harrison Barnes F 41:55 10 14 4 7 4 5 1 5 6 6 2 0 3 0 10 28 35 Marvin Bagley III F 34:56 11 20 2 5 0 2 4 6 10 1 2 2 1 1 18 24 22 Richaun Holmes C 33:42 5 8 0 1 3 3 1 7 8 1 4 2 0 1 0 13 24 Buddy Hield G 38:49 10 17 8 15 2 3 0 2 2 7 3 0 1 0 12 30 5 De'Aaron Fox G 40:33 9 22 1 3 1 4 0 1 1 14 4 1 2 0 -3 20 8 Nemanja Bjelica 21:31 5 6 1 1 0 0 0 2 2 1 2 1 1 0 -12 11 9 Cory Joseph 16:06 0 3 0 2 0 0 2 0 2 2 1 0 2 0 -20 0 19 DaQuan Jeffries 12:28 0 2 0 2 0 0 1 1 2 0 1 0 0 0 -10 0 7 Kyle Guy DNP - Coach's decision 10 Justin James DNP - Coach's decision 33 Jabari Parker NWT - Health and Safety Protocols 14 Norvel Pelle DNP - Coach's decision 240:00 50 92 16 36 10 17 9 24 33 32 19 6 10 2 -1 126 54.3% 44.4% 58.8% TM REB: 8 TOT TO: 10 (13 PTS) SCORE BY PERIOD 1 2 3 4 FINAL Hornets 36 30 22 39 127 KINGS 39 28 29 30 126 Inactive: Hornets - Carey Jr. -

May 12 Redemption Update
SET SUBSET/INSERT # PLAYER 2016 Panini Immaculate Collection Baseball Immaculate Marks Red 19 Roger Clemens 2014 Donruss Base Brand Donruss Baseball Donruss Signatures 40 Xander Bogaerts 2016 Panini Absolute (16-17) Basketball Glass 1 Ben Simmons 2016 Panini Absolute (16-17) Basketball Glass 2 Brandon Ingram 2016 Panini Absolute (16-17) Basketball Glass 3 Kris Dunn 2016 Panini Absolute (16-17) Basketball Glass 4 Jaylen Brown 2016 Panini Absolute (16-17) Basketball Glass 5 Buddy Hield 2016 Panini Absolute (16-17) Basketball Glass 6 Jamal Murray 2016 Panini Absolute (16-17) Basketball Glass 7 Anthony Davis 2016 Panini Absolute (16-17) Basketball Glass 8 Kyrie Irving 2016 Panini Absolute (16-17) Basketball Glass 9 Kevin Durant 2016 Panini Absolute (16-17) Basketball Glass 10 Chris Paul 2016 Panini Absolute (16-17) Basketball Glass 11 Karl-Anthony Towns 2016 Panini Absolute (16-17) Basketball Glass 12 Russell Westbrook 2016 Panini Absolute (16-17) Basketball Glass 13 Andrew Wiggins 2016 Panini Absolute (16-17) Basketball Glass 14 Stephen Curry 2016 Panini Absolute (16-17) Basketball Glass 15 LeBron James 2016 Panini Absolute (16-17) Basketball Glass 16 Kawhi Leonard 2016 Panini Absolute (16-17) Basketball Glass 17 Dirk Nowitzki 2016 Panini Absolute (16-17) Basketball Glass 18 Jimmy Butler 2016 Panini Absolute (16-17) Basketball Glass 19 James Harden 2016 Panini Absolute (16-17) Basketball Glass 20 Karl Malone 2016 Panini Absolute (16-17) Basketball Glass 21 Kobe Bryant 2016 Panini Absolute (16-17) Basketball Glass 22 Steve Nash 2016 Panini