DOCSLIB.ORG

Polynomials Notes (Answers)

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Polynomials Notes (Answers) Pure Math 10 Notes Unit 1: Polynomials Unit 1: Polynomials 3-1: Reviewing Polynomials Expressions: - mathematical sentences with no equal sign. Example: 3x + 2 Equations: - mathematical sentences that are equated with an equal sign. Example: 3x + 2 = 5x + 8 Terms: - are separated by an addition or subtraction sign. - each term begins with the sign preceding the variable or coefficient. Numerical Coefficient Monomial: - one term expression. Example: 5x2 Exponent Variable Binomial: - two terms expression. Example: 5x2 + 5x Trinomial: - three terms expression. Example: x2 + 5x + 6 Polynomial: - many terms (more than one) expression. All Polynomials must have whole numbers as exponents!! 1 Example: 9x −1 +12x 2 is NOT a polynomial. Degree: - the term of a polynomial that contains the largest sum of exponents Example: 9x2y3 + 4x5y2 + 3x4 Degree 7 (5 + 2 = 7) Example 1: Fill in the table below. Polynomial Number of Terms Classification Degree Classified by Degree 9 1 monomial 0 constant 4x 1 monomial 1 linear 9x + 2 2 binomial 1 linear x2 − 4x + 2 3 trinomial 2 quadratic 2x3 − 4x2 + x + 9 4 polynomial 3 cubic 4x4 − 9x + 2 3 trinomial 4 quartic Like Terms: - terms that have the same variables and exponents. Examples: 2x2y and 5x2y are like terms 2x2y and 5xy2 are NOT like terms Copyrighted by Gabriel Tang, B.Ed., B.Sc. Page 1. Unit 1: Polynomials Pure Math 10 Notes To Add and Subtract Polynomials: Combine like terms by adding or subtracting their numerical coefficients. Example 2: Simplify the followings. a. 3x2 + 5x − x2 + 4x − 6 b. (9x2y3 + 4x3y2) + (3x3y2 −10x2y3) = 3x2 + 5x − x2 + 4x − 6 = 9x2y3 + 4x3y2 + 3x3y2 −10x2y3 = 2x2 + 9x − 6 = −x2y3 + 7x3y2 c. (9x2y3 + 4x3y2) − (3x3y2 −10x2y3) = 9x2y3 + 4x3y2 − 3x3y2 + 10x2y3 (drop brackets and switch signs in the bracket that had − sign in front of it) = 19x2y3 + x3y2 9x 2 + 4x d. Subtract This is the same as (9x2 + 4x) − (5x2 −7x) 5x 2 − 7x = 9x2 + 4x − 5x2 + 7x = 4x2 + 11x To Multiply and Divide Monomials: Multiply or Divide (Reduce) Numerical Coefficients. Add or Subtract exponents of the same variable according to basic exponential laws. Example 3: Simplify the followings. 24x7 y 4 z 5 75a3b4 a. (3x3y2) (7x2y4) b. c. 6x3 yz 5 25a5b3 24 x7 y 4 z 5 75 a3 b4 = (3)(7) (x3)(x2) (y2)(y4) = = 3 5 5 3 6 x y z 25 a b 3b = 21x5y6 = 4x4y3z0 ( z0 = 1 ) = 3a−2b or a 2 = 4x4y3 Page 2. Copyrighted by Gabriel Tang, B.Ed., B.Sc. Pure Math 10 Notes Unit 1: Polynomials (AP) Example 4: Find the area of the following ring. General Formula for Area of a Circle A = πr2 Inner Circle Radius = 2x Outer Circle Radius = (2x + 4x) = 6x Inner Circle Area: A = π (2x)2 A = π (4x2) 4x 4x A = 4πx2 Outer Circle Area: A = π (6x)2 A = π (36x2) A = 36πx2 Shaded Area = 36πx2 − 4πx2 Shaded Area = 32πx2 3-1 Homework Assignment Regular: pg. 102-103 #1 to 51, 55, 56 AP: pg. 102-103 #1 to 51, 53-57 Copyrighted by Gabriel Tang, B.Ed., B.Sc. Page 3. Unit 1: Polynomials Pure Math 10 Notes 3-3: Multiplying Polynomials To Multiply Monomials with Polynomials Example 1: Simplify the followings. a. 3 (2x2 − 4x + 7) b. 2x (3x2 + 2x − 4) = 3 (2x2 − 4x + 7) = 2x (3x2 + 2x − 4) = 6x2 − 12x + 21 = 6x3 + 4x2 − 8x c. 3x (5x + 4) − 4 (x2 − 3x) d. 8 (a2 − 2a + 3) − 4 − (3a2 + 7) (only multiply = 3x (5x + 4) − 4 (x2 − 3x) the brackets = 8 (a2 − 2a + 3) − 4 − (3a2 + 7) right after the = 15x2 + 12x − 4x2 + 12x monomial) = 8a2 − 16a + 24 − 4 − 3a2 − 7 = 11x2 + 24x = 5a2 − 16a + 13 To Multiply Polynomials with Polynomials Example 2: Simplify the followings. a. (3x + 2) (4x −3) b. (x + 3) (2x2 − 5x + 3) = (3x + 2) (4x −3) = (x + 3) (2x2 − 5x + 3) = 12x2 − 9x + 8x − 6 = 2x3 − 5x2 + 3x + 6x2 − 15x + 9 = 12x2 − x − 6 = 2x3 + x2 − 12x + 9 c. 3 (x + 2) (2x + 3) − (2x − 1) (x + 3) d. (x2 − 2x + 1) (3x2 + x − 4) = 3 (x + 2) (2x + 3) − (2x − 1) (x + 3) = (x2 − 2x + 1) (3x2 + x − 4) = 3 (2x2 − 3x + 4x − 6) − (2x2 + 6x − x − 3) = 3x4 + x3 − 4x2 −6x3 − 2x2 + 8x + 3x2 + x − 4 = 3 (2x2 + x − 6) − (2x2 + 5x − 3) = 6x2 + 3x − 18 − 2x2 − 5x + 3 = 3x4 − 5x3 − 3x2 + 9x − 4 = 4x2 − 2x − 15 Page 4. Copyrighted by Gabriel Tang, B.Ed., B.Sc. Pure Math 10 Notes Unit 1: Polynomials Example 3: Find the shaded area of each of the followings. a. 5x + 4 b. 7x − 2 x + 2 3x + 1 x + 1 2x − 1 Shaded Area = Big Rectangle − Small Square x + 5 7x − 2 = (5x + 4) (2x − 1) − (x + 1) (x + 1) = (10x2 − 5x + 8x − 4) − (x2 + x + x + 1) x + 2 x + 2 = (10x2 + 3x − 4) − (x2 + 2x + 1) = 10x2 + 3x − 4 − x2 − 2x − 1 Shaded Area = 9x2 + x − 5 x + 5 (3x + 1) − (x + 2) = 2x − 1 Total Area = Top Rectangle + Bottom Rectangle = (7x −2) (x + 2) + (2x − 1) (x + 5) = (7x2 + 14x − 2x − 4) + (2x2 + 10x − x − 5) = (7x2 + 12x − 4) + (2x2 + 9x − 5) = 7x2 + 12x − 4 + 2x2 + 9x − 5 Total Area = 9x2 + 21x − 9 3-3 Homework Assignment Regular: pg. 107-109 #1 to 77 (odd), 87, 88 AP: pg. 107-109 #2 to 84 (even) , 85, 87, 88, 91 Copyrighted by Gabriel Tang, B.Ed., B.Sc. Page 5. Unit 1: Polynomials Pure Math 10 Notes 3-4: Special Products (x + y)2 = (x + y) (x + y) (x + y)2 is NOT x2 + y2 (x + y)3 = (x + y) (x + y) (x + y) Example 1: Simplify the followings. a. (2x + 3)2 b. (x − 2)3 = (2x + 3) (2x + 3) = (x − 2) (x − 2) (x − 2) = 4x2 + 6x + 6x + 9 = (x − 2) (x2 − 2x − 2x + 4) = 4x2 + 12x + 9 = (x − 2) (x2 − 4x + 4) = x3 − 4x2 + 4x − 2x 2 + 8x − 8 = x3 − 6x2 + 12x − 8 c. (3x + 2)2 − (2x − 1)2 Example 2: Find the volume of the box below. = (3x + 2) (3x + 2) − (2x − 1) (2x − 1) = (9x2 + 6x + 6x + 4) − (4x2 − 2x − 2x + 1) 2x + 1 = (9x2 + 12x + 4) − (4x2 − 4x + 1) 3x − 1 = 9x2 + 12x + 4 − 4x2 + 4x − 1 3x − 1 = 5x2 + 16x + 3 Volume = Length × Width × Height V = (3x − 1)2 (2x + 1) 3-4 Homework Assignment V = (9x2 − 3x − 3x + 1) (2x + 1) Regular: pg.112-113 #1 to 47 (odd), 49, 51, 54 (a, c, e, g), 55 (a, c, e, g), 56 V = (9x2 − 6x + 1) (2x + 1) AP: pg.112-113 #2 to 48 (even), 49 to 53, V = 18x3 + 9x2 − 12x2 − 6x + 2x + 1 54 (b, d, f, h), 55 (b, d, f, h), 56, 57 Volume = 18x3 − 3x2 − 4x + 1 Page 6. Copyrighted by Gabriel Tang, B.Ed., B.Sc. Pure Math 10 Notes Unit 1: Polynomials 3-6: Common Factors Common Factors can consist of two parts: a. Numerical GCF: - Greatest Common Factor of all numerical coefficients and constant. b. Variable GCF: - the lowest exponent of a particular variable. After obtaining the GCF, use it to divide each term of the polynomial for the remaining factor. Example 1: Factor the followings a. 3x2 + 6x + 12 b. 4a2b − 8ab2 + 6ab GCF = 3 GCF = 2ab = 3 (x2 + 2x + 4) = 2ab (2a − 4b + 3) Factor by Grouping (Common Brackets as GCF) a (c + d) + b (c + d) = (c + d) (a + b) Common Brackets Take common bracket out as GCF Example 2: Factor. a. 3x (2x − 1) + 4 (2x − 1) b. 2ab + 3ac + 4b2 + 6bc = (2x − 1) (3x + 4) = (2ab + 3ac) + (4b2 + 6bc) = a (2b + 3c) + 2b (2b + 3c) = (2b + 3c) (a + 2b) c. 3x2 − 6y2 + 9x − 2xy2 = (3x2 − 6y2) + (9x − 2xy2) = 3 (x2 − 2y2) + x (9 − 2y2) Brackets are NOT the same! We might have to first rearrange terms. Try again after rearranging terms! 3x2 + 9x − 2xy2 − 6y2 = (3x2 + 9x) − (2xy2 + 6y2) Switch Sign in Second Bracket! 2 We have put a minus sign in front of a new = 3x (x + 3) − 2y (x + 3) bracket! = (x + 3) (3x − 2y2) Copyrighted by Gabriel Tang, B.Ed., B.Sc. Page 7. Unit 1: Polynomials Pure Math 10 Notes Example 3: Find the area of the shaded region in factored form and as a polynomial. Shaded Area = Area of Square − Area of Circle 2 x Shaded Area = x2 − π x 2 πx 2 Shaded Area = x2 − (Polynomial Form) 4 π Shaded Area = x 2 1− (Factored Form) 4 Area of a Circle A = πr2 x Radius of Circle = 2 3-6 Homework Assignments Regular: pg. 120 #1 to 35 (odd), 38 to 43 AP: pg.120 #2 to 36 (even), 37 to 44 Page 8. Copyrighted by Gabriel Tang, B.Ed., B.Sc. Pure Math 10 Notes Unit 1: Polynomials 3-8: Factoring x2 + bx + c (Leading Coefficient is 1) x2 + bx + c What two numbers multiply to give c, but add up to be b? Example 1: Completely factor the followings. 2 Product of 6 2 a. x + 5x + 6 b. x − 3x − 10 Product of −10 1 6 −1 −6 −1 10 1 −10 2 3 = (x + 2) (x + 3) −2 − 3 = (x + 2) (x −5) −2 5 2 −5 sum of 5 sum of −3 Product of 15 c. a2 − 8a + 15 d. x2 − 7xy + 12y2 Product of 12 1 15 −1 −15 1 12 −1 −12 3 5 = (a − 3) (a − 5) −3 − 5 = (x − 3y) (x −4y) 2 6 −2 −6 3 4 −3 −4 sum of −8 sum of −7 e. x2y2 − 6xy − 16 Product of −16 f. 14 – 5w − w2 −1 16 1 −16 Rearrange in = (xy + 2) (xy − 8) −2 8 2 −8 = −w2 − 5w + 14 Descending Degree.
Load more

Recommended publications
  • Algebraic Number Theory
    Algebraic Number Theory William B. Hart Warwick Mathematics Institute Abstract. We give a short introduction to algebraic number theory. Algebraic number theory is the study of extension fields Q(α1; α2; : : : ; αn) of the rational numbers, known as algebraic number fields (sometimes number fields for short), in which each of the adjoined complex numbers αi is algebraic, i.e. the root of a polynomial with rational coefficients. Throughout this set of notes we use the notation Z[α1; α2; : : : ; αn] to denote the ring generated by the values αi. It is the smallest ring containing the integers Z and each of the αi. It can be described as the ring of all polynomial expressions in the αi with integer coefficients, i.e. the ring of all expressions built up from elements of Z and the complex numbers αi by finitely many applications of the arithmetic operations of addition and multiplication. The notation Q(α1; α2; : : : ; αn) denotes the field of all quotients of elements of Z[α1; α2; : : : ; αn] with nonzero denominator, i.e. the field of rational functions in the αi, with rational coefficients. It is the smallest field containing the rational numbers Q and all of the αi. It can be thought of as the field of all expressions built up from elements of Z and the numbers αi by finitely many applications of the arithmetic operations of addition, multiplication and division (excepting of course, divide by zero). 1 Algebraic numbers and integers A number α 2 C is called algebraic if it is the root of a monic polynomial n n−1 n−2 f(x) = x + an−1x + an−2x + ::: + a1x + a0 = 0 with rational coefficients ai.
    [Show full text]
  • Fields Besides the Real Numbers Math 130 Linear Algebra
    manner, which are both commutative and asso- ciative, both have identity elements (the additive identity denoted 0 and the multiplicative identity denoted 1), addition has inverse elements (the ad- ditive inverse of x denoted −x as usual), multipli- cation has inverses of nonzero elements (the multi- Fields besides the Real Numbers 1 −1 plicative inverse of x denoted x or x ), multipli- Math 130 Linear Algebra cation distributes over addition, and 0 6= 1. D Joyce, Fall 2015 Of course, one example of a field is the field of Most of the time in linear algebra, our vectors real numbers R. What are some others? will have coordinates that are real numbers, that is to say, our scalar field is R, the real numbers. Example 2 (The field of rational numbers, Q). Another example is the field of rational numbers. But linear algebra works over other fields, too, A rational number is the quotient of two integers like C, the complex numbers. In fact, when we a=b where the denominator is not 0. The set of discuss eigenvalues and eigenvectors, we'll need to all rational numbers is denoted Q. We're familiar do linear algebra over C. Some of the applications with the fact that the sum, difference, product, and of linear algebra such as solving linear differential quotient (when the denominator is not zero) of ra- equations require C as as well. tional numbers is another rational number, so Q Some applications in computer science use linear has all the operations it needs to be a field, and algebra over a two-element field Z (described be- 2 since it's part of the field of the real numbers R, its low).
    [Show full text]
  • Ring (Mathematics) 1 Ring (Mathematics)
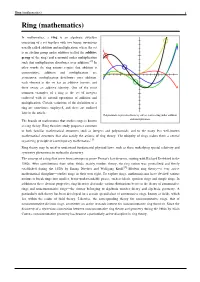
    Ring (mathematics) 1 Ring (mathematics) In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition (called the additive group of the ring) and a monoid under multiplication such that multiplication distributes over addition.a[›] In other words the ring axioms require that addition is commutative, addition and multiplication are associative, multiplication distributes over addition, each element in the set has an additive inverse, and there exists an additive identity. One of the most common examples of a ring is the set of integers endowed with its natural operations of addition and multiplication. Certain variations of the definition of a ring are sometimes employed, and these are outlined later in the article. Polynomials, represented here by curves, form a ring under addition The branch of mathematics that studies rings is known and multiplication. as ring theory. Ring theorists study properties common to both familiar mathematical structures such as integers and polynomials, and to the many less well-known mathematical structures that also satisfy the axioms of ring theory. The ubiquity of rings makes them a central organizing principle of contemporary mathematics.[1] Ring theory may be used to understand fundamental physical laws, such as those underlying special relativity and symmetry phenomena in molecular chemistry. The concept of a ring first arose from attempts to prove Fermat's last theorem, starting with Richard Dedekind in the 1880s. After contributions from other fields, mainly number theory, the ring notion was generalized and firmly established during the 1920s by Emmy Noether and Wolfgang Krull.[2] Modern ring theory—a very active mathematical discipline—studies rings in their own right.
    [Show full text]
  • A Brief History of Ring Theory
    A Brief History of Ring Theory by Kristen Pollock Abstract Algebra II, Math 442 Loyola College, Spring 2005 A Brief History of Ring Theory Kristen Pollock 2 1. Introduction In order to fully define and examine an abstract ring, this essay will follow a procedure that is unlike a typical algebra textbook. That is, rather than initially offering just definitions, relevant examples will first be supplied so that the origins of a ring and its components can be better understood. Of course, this is the path that history has taken so what better way to proceed? First, it is important to understand that the abstract ring concept emerged from not one, but two theories: commutative ring theory and noncommutative ring the- ory. These two theories originated in different problems, were developed by different people and flourished in different directions. Still, these theories have much in com- mon and together form the foundation of today's ring theory. Specifically, modern commutative ring theory has its roots in problems of algebraic number theory and algebraic geometry. On the other hand, noncommutative ring theory originated from an attempt to expand the complex numbers to a variety of hypercomplex number systems. 2. Noncommutative Rings We will begin with noncommutative ring theory and its main originating ex- ample: the quaternions. According to Israel Kleiner's article \The Genesis of the Abstract Ring Concept," [2]. these numbers, created by Hamilton in 1843, are of the form a + bi + cj + dk (a; b; c; d 2 R) where addition is through its components 2 2 2 and multiplication is subject to the relations i =pj = k = ijk = −1.
    [Show full text]
  • Subrings, Ideals and Quotient Rings the First Definition Should Not Be
    Section 17: Subrings, Ideals and Quotient Rings The first definition should not be unexpected: Def: A nonempty subset S of a ring R is a subring of R if S is closed under addition, negatives (so it's an additive subgroup) and multiplication; in other words, S inherits operations from R that make it a ring in its own right. Naturally, Z is a subring of Q, which is a subring of R, which is a subring of C. Also, R is a subring of R[x], which is a subring of R[x; y], etc. The additive subgroups nZ of Z are subrings of Z | the product of two multiples of n is another multiple of n. For the same reason, the subgroups hdi in the various Zn's are subrings. Most of these latter subrings do not have unities. But we know that, in the ring Z24, 9 is an idempotent, as is 16 = 1 − 9. In the subrings h9i and h16i of Z24, 9 and 16 respectively are unities. The subgroup h1=2i of Q is not a subring of Q because it is not closed under multiplication: (1=2)2 = 1=4 is not an integer multiple of 1=2. Of course the immediate next question is which subrings can be used to form factor rings, as normal subgroups allowed us to form factor groups. Because a ring is commutative as an additive group, normality is not a problem; so we are really asking when does multiplication of additive cosets S + a, done by multiplying their representatives, (S + a)(S + b) = S + (ab), make sense? Again, it's a question of whether this operation is well-defined: If S + a = S + c and S + b = S + d, what must be true about S so that we can be sure S + (ab) = S + (cd)? Using the definition of cosets: If a − c; b − d 2 S, what must be true about S to assure that ab − cd 2 S? We need to have the following element always end up in S: ab − cd = ab − ad + ad − cd = a(b − d) + (a − c)d : Because b − d and a − c can be any elements of S (and either one may be 0), and a; d can be any elements of R, the property required to assure that this element is in S, and hence that this multiplication of cosets is well-defined, is that, for all s in S and r in R, sr and rs are also in S.
    [Show full text]
  • Define the Determinant of A, to Be Det(A) = Ad − Bc. EX
    DETERMINANT 1. 2 × 2 Determinants Fix a matrix A 2 R2×2 a b A = c d Define the determinant of A, to be det(A) = ad − bc: 2 −1 EXAMPLE: det = 2(2) − (−1)(−4) = 0. −4 2 det(A) encodes important geometric and algebraic information about A. For instance, the matrix A is invertible if and only if det(A) 6= 0. To see this suppose det(A) 6= 0, in this case the matrix 1 d −b B = det A −c a is well-defined. One computes, 1 ad − bc 0 BA = = I : ad − bc 0 ad − bc 2 and so A is invertible and A−1 = B. In the other direction, if A is not invertible, then the columns are linearly dependent and so either a = kb and c = kd or b = ka and d = kc for some k 2 R. Hence, det(A) = kbd − kbd = 0 or = kac − kac = 0. More geometrically, if x1 S = : 0 ≤ x1; x2 ≤ 1 x2 is the unit square and A(S) = fA~x : ~x 2 Sg is the image under multiplication by A of S, then the area of A(S), which we denote by jA(S)j is jA(S)j = j det(A)j: 2. Determinants of n × n matrices We seek a good notion for det(A) when A 2 Rn×n. It is improtant to remember that while this is of historical and theoretical importance, it is not as significant for computational purposes. Begin by fixing a matrix A 2 Rn×n of the form 2 3 a11 ··· a1n 6 .
    [Show full text]
  • Number Fields
    Part II | Number Fields Based on lectures by I. Grojnowski Notes taken by Dexter Chua Lent 2016 These notes are not endorsed by the lecturers, and I have modified them (often significantly) after lectures. They are nowhere near accurate representations of what was actually lectured, and in particular, all errors are almost surely mine. Part IB Groups, Rings and Modules is essential and Part II Galois Theory is desirable Definition of algebraic number fields, their integers and units. Norms, bases and discriminants. [3] Ideals, principal and prime ideals, unique factorisation. Norms of ideals. [3] Minkowski's theorem on convex bodies. Statement of Dirichlet's unit theorem. Deter- mination of units in quadratic fields. [2] Ideal classes, finiteness of the class group. Calculation of class numbers using statement of the Minkowski bound. [3] Dedekind's theorem on the factorisation of primes. Application to quadratic fields. [2] Discussion of the cyclotomic field and the Fermat equation or some other topic chosen by the lecturer. [3] 1 Contents II Number Fields Contents 0 Introduction 3 1 Number fields 4 2 Norm, trace, discriminant, numbers 10 3 Multiplicative structure of ideals 17 4 Norms of ideals 27 5 Structure of prime ideals 32 6 Minkowski bound and finiteness of class group 37 7 Dirichlet's unit theorem 48 8 L-functions, Dirichlet series* 56 Index 68 2 0 Introduction II Number Fields 0 Introduction Technically, IID Galois Theory is not a prerequisite of this course. However, many results we have are analogous to what we did in Galois Theory, and we will not refrain from pointing out the correspondence.
    [Show full text]
  • RING THEORY 1. Ring Theory a Ring Is a Set a with Two Binary Operations
    CHAPTER IV RING THEORY 1. Ring Theory A ring is a set A with two binary operations satisfying the rules given below. Usually one binary operation is denoted `+' and called \addition," and the other is denoted by juxtaposition and is called \multiplication." The rules required of these operations are: 1) A is an abelian group under the operation + (identity denoted 0 and inverse of x denoted x); 2) A is a monoid under the operation of multiplication (i.e., multiplication is associative and there− is a two-sided identity usually denoted 1); 3) the distributive laws (x + y)z = xy + xz x(y + z)=xy + xz hold for all x, y,andz A. Sometimes one does∈ not require that a ring have a multiplicative identity. The word ring may also be used for a system satisfying just conditions (1) and (3) (i.e., where the associative law for multiplication may fail and for which there is no multiplicative identity.) Lie rings are examples of non-associative rings without identities. Almost all interesting associative rings do have identities. If 1 = 0, then the ring consists of one element 0; otherwise 1 = 0. In many theorems, it is necessary to specify that rings under consideration are not trivial, i.e. that 1 6= 0, but often that hypothesis will not be stated explicitly. 6 If the multiplicative operation is commutative, we call the ring commutative. Commutative Algebra is the study of commutative rings and related structures. It is closely related to algebraic number theory and algebraic geometry. If A is a ring, an element x A is called a unit if it has a two-sided inverse y, i.e.
    [Show full text]
  • UNIT-REGULAR ORTHODOX SEMIGROUPS by R
    UNIT-REGULAR ORTHODOX SEMIGROUPS by R. B. McFADDEN (Received 5 May, 1983) Introduction. Unit-regular rings were introduced by Ehrlich [4]. They arose in the search for conditions on a regular ring that are weaker than the ACC, DCC, or finite Goldie dimension, which with von Neumann regularity imply semisimplicity. An account of unit-regular rings, together with a good bibliography, is given by Goodearl [5]. The basic definition of unit-regularity is purely multiplicative; it is simply that for each element x of a monoid S (initially a ring R with identity) there is a unit u of S for which x = xux. The concept of a unit-regular semigroup is a natural one; for example, the full transformation semigroup on a finite set, and the semigroup of endomorphisms of a finite-dimensional vector space, are unit-regular semigroups [1]. Unit-regularity has been studied by Chen and Hsieh [2], by Tirasupa [9], and by McAlister [6]. The connection between unit-regularity and finiteness conditions has been considered by D'Alarcao [3]. The problem of describing the structure of an arbitrary unit-regular semigroup S is difficult. It appears reasonable to attempt to provide such a description in terms of the group of units of S and the set of idempotents of S, and in this direction Blyth and McFadden did determine the structure of a narrow class of unit-regular semigroups. Calling a semigroup S uniquely unit orthodox if it is orthodox and, for each x in S, there exists a unique unit u of S for which x = xux, they proved that every such semigroup is a semidirect product of a group (the group of units of S) and a band (the band of idempotents of S).
    [Show full text]
  • Math 6370: Algebraic Number Theory
    Math 6370: Algebraic Number Theory Taught by David Zywina Notes by David Mehrle [email protected] Cornell University Spring 2018 Last updated May 13, 2018. The latest version is online here. Contents 1 Introduction................................. 5 1.1 Administrivia............................. 8 2 Algebraic integers.............................. 9 2.1 Trace and Norm............................. 11 2.2 Complex embeddings ........................ 13 2.3 OK as an abelian group........................ 16 2.4 Discriminants............................. 18 2.5 Example: Cyclotomic Integers.................... 25 3 The ideal class group............................ 28 3.1 Unique Factorization......................... 29 3.2 Fractional Ideals............................ 34 3.3 Ramification.............................. 40 3.4 Dedekind Domains.......................... 44 3.5 Discrete Valuation Rings....................... 46 3.6 Extensions of number fields. .................... 48 4 Geometry of Numbers (Minkowski Theory)............... 50 4.1 Algebraic integers as a lattice .................... 53 4.2 Minkowski’s Theorem........................ 54 4.3 The class group is finite........................ 57 4.4 Bounds on the Discriminant...................... 61 4.5 Bounds on the Discriminant..................... 66 5 The units of OK ............................... 68 5.1 Dirichlet Unit Theorem and Examples............... 69 5.2 Pell’s Equation.............................. 71 5.3 Proof of the Dirichlet Unit Theorem ................ 73 6 Galois
    [Show full text]
  • THE STRUCTURE of UNIT GROUPS Contents 1. Units of Z[ √ D] 1 2
    THE STRUCTURE OF UNIT GROUPS DANIEL KLINE Abstract. Since the time of ancient Greece and India, Pell's equation, a2 − 2 db = 1, has been studied and its solutions sought after. Thesep solutions are significant, because they correspond to the units of the rings Z[ d]. Along with prime numbers, units are vital in understanding the structure and especially the factorization within different rings. Dirichlect's Unit Theorem establishes the structure of the units of a number field as a finite abelian group. In addition to describing the nature of units, Dirichlect's Unit Theorem represents the interconnectedness of geometry (namely Minkowski's Theorem), algebra, and number theory. Contents p 1. Units of Z[ d] 1 2. Minkowski's Theorem in the Plane 3 3. Minkowski's Theorem in General 5 4. Basic Properties of Number Fields 6 5. Algebraic Integers 9 6. Real and Imaginary Embeddings 10 7. Dirichlet's Unit Theorem 10 Acknowledgments 14 References 14 p 1. Units of Z[ d] Definition 1.1. Given a ring R, u 2 R is a unit if there exists v 2 R such that u · v = 1. We denote the set of units of a ring R as R∗. Example 1.2. Consider the ring Z. It is easy to check that Z∗ = {±1g. Units are not generally as obvious as inp the case of Z. Throughout this section, we will considerp the ringsp of the form Z[ d] where d is a square-free integer. We define Z[ d] := fa + b d j a; b 2 Zg. For identifying units of rings in this form, we will rely on the useful property that the norm of a unit, which we will define below, is equal to ±1.
    [Show full text]
  • POLYNOMIALS DEFINING MANY UNITS Let G Be a Group and Let ZG
    POLYNOMIALS DEFINING MANY UNITS OSNEL BROCHE AND ANGEL´ DEL R´IO Abstract. We classify the polynomials with integral coefficients that, when evaluated on a group element of finite order n, define a unit in the integral group ring for infinitely many positive integers n. We show that this happens if and only if the polynomial defines generic units in the sense of Marciniak and Sehgal. We also classify the polynomials with integral coefficients which provides units when evaluated on n-roots of a fixed integer a for infinitely many positive integers n. Let G be a group and let ZG denote the integral group ring of G. If x 2 G and f is a polynomial in one variable with integral coefficients then f(x) denotes the element of ZG obtained when f is evaluated in x. This paper deals with the problem of when f(x) is a unit of ZG. It is easy to see that this only depends on the order (possibly infinite) of x. If the order of x is infinite and f(x) is a unit then necessarily f = ±Xm for some non-negative integer m. Hence we are only interested in the case where x has finite order. In case f(x) is a unit of ZG and n is the order of x then we say that f defines a unit on order n. Marciniak and Sehgal introduced the following definition [MS05]. A polynomial f defines generic units if there is a positive integer D such that f defines a unit on every order coprime with D.
    [Show full text]