DOCSLIB.ORG

Many Electrons and the Photon Field the Many-Body Structure of Nonrelativistic Quantum Electrodynamics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Many Electrons and the Photon Field the Many-Body Structure of Nonrelativistic Quantum Electrodynamics Many Electrons and the Photon Field The many-body structure of nonrelativistic quantum electrodynamics vorgelegt von M. Sc. Florian Konrad Friedrich Buchholz ORCID: 0000-0002-9410-4892 an der Fakultät II – Mathematik und Naturwissenschaften der Technischen Universität Berlin zur Erlangung des akademischen Grades DOKTOR DER NATURWISSENSCHAFTEN Dr.rer.nat. genehmigte Dissertation PROMOTIONSAUSSCHUSS: Vorsitzende: Prof. Dr. Ulrike Woggon Gutachter: Prof. Dr. Andreas Knorr Gutachter: Dr. Michael Ruggenthaler Gutachter: Prof. Dr. Angel Rubio Gutachter: Prof. Dr. Dieter Bauer Tag der wissenschaftlichen Aussprache: 24. November 2020 Berlin 2021 ACKNOWLEDGEMENTS The here presented work is the result of a long process that naturally involved many different people. They all contributed importantly to it, though in more or less explicit ways. First of all, I want to express my gratitude to Chiara, all my friends and my (German and Italian) family. Thank you for being there! Next, I want to name Michael Ruggenthaler, who did not only supervise me over many years, contribut- ing crucially to the here presented research, but also has become a dear friend. I cannot imagine how my time as a PhD candidate would have been without you! In the same breath, I want to thank Iris Theophilou, who saved me so many times from despair over non-converging codes and other difficult moments. Also without you, my PhD would not have been the same. Then, I thank Angel Rubio for his supervision and for making possible my unforgettable and formative time at the Max-Planck Institute for the Structure and Dynamics of Matter. There are few people who have the gift to make others feel so excited about physics, as Angel does. Heiko Appel supervised my first steps in the scientific environment and remained also afterwards always close. His excitement for unusual questions and ideas greatly influenced my projects and work. Nobody inspired my idea of what science really is more than Markus Penz. He regularly shows with great confidence how to think out of the box and to question things beyond traditional boundaries. Then I want to name Micael Oliveira the great tamer of the Octopus. He taught me not only to implement, but to develop. I thank Henning Glawe for being patient with me and for using his supernatural powers to make the penguin regain his feet, whenever I made it fall. Warm thanks go to my dear friends Björn Bembnista and Wilhelm Bender for the many stimulating nights of discussion about physics and for sharing their great knowledge about coding and minimization. I also want to thank Vasilis Rokaj, Davis Welakuh, Christian Schäfer, Guillem Albareda, Arun Debnath, Nicolas Tancogne-Dejean, Florian Eich, Michael Sentef, Enrico Ronca, Massimo Altarelli and Martin Lüders for many interesting discussions. Warm thanks goes to Uliana Mordovina, Teresa Reinhard, Christian Schäfer, Mary-Leena Tchenkoue Djouom, Norah Hoffmann and Alexandra Göbel for sharing the precious moments with me, where we needed to forget science. I thank Fabio Covito, Simone Latini, Matteo Vandelli, and Enrico Ronca for sharing coffee and the feeling of sunny places. And I thank Ute Ramseger, Graciela Sanguino, Kathja Schroeder and Frauke Kleinwort for their big efforts to support us PhD students at the Institute. Sarah Loos contributed not only to my scientific world view in many inspiring discussions, but also di- rectly to this thesis by her indispensable feedback, understanding what I wanted to say before I did. I also want to thank David Licht and Chiara for valuable feedback on my thesis, and Uliana for help with the lay- out. Furthermore, I want to mention Michael Duszat and the “deep readers,” who made me aware on how much information only one sentences may contain and who were the very first audience for this thesis. I also want to thank all the many authors that have contributed to making the various STACKEXCHANGE pages such a valuable platform with answers to so many difficult questions. Finally, I want to mention the other members of the Basic Research Community For Physics. It is so inspir- ing to know so many people who share the believe in a cooperative, respectful and open-minded scientific research inside and outside traditional institutions. i ii ZUSAMMENFASSUNG Neueste experimentelle Fortschritte im Bereich von “Cavity”-Quantenelektrodynamik ermöglichen die Er- forschung der starken Wechselwirkung zwischen quantisiertem Licht und komplexen Materiesystemen. Aufgrund der kohärenten Kopplung zwischen Photonen und Materiefreiheitsgraden, entstehen Polarito- nen, hybride Licht-Materie Quasiteilchen, die dazu beitragen können, Materieeigenschaften und komplexe Prozesse wie chemische Reaktionen entscheidend zu beeinflussen. Dieses Regime der starken Kopplung er- öffnet Möglichkeiten zur Kontrolle von Materialien und Chemie in einer beispiellosen weise. Allerdings sind die genauen Mechanismen hinter vielen solcher Phänomene nicht vollständig verstanden. Ein wichtiger Grund dafür ist, dass das physikalische Problem oft mit äußerst vereinfachten Methoden beschrieben wird, wobei die Materie zu wenigen effektiven "Levels"reduziert wird. Akkuratere first-principles Methoden, die Photonen gleichwertig zu Elektronen behandeln entstehen nur langsam, da die Erforschung solcher Metho- den sowohl durch die erhöhte Komplexität der kombinierten Elektron-Photon Wellenfunktionen, als auch dem Fakt, dass zwei verschiedene Teilchenspezies miteinbezogen werden müssen, aufgehalten wird. In dieser Doktorarbeit schlagen wir vor diese Problem zu umgehen, indem das gekoppelte Elektron- Photon Problem exakt in einem anderen zweckgebauten Hilbertraum neuformuliert wird. Dadurch, dass wir ein System, bestehend aus N Elektronen und M Moden, mit einer N-Polaritonen Wellenfunktion re- präsentieren, können wir explizit zeigen wie ein electronic-structure in eine polaritonic-structure Methode umgewandelt werden kann, die für schwache bis hin zu starken Kopplungstärken akkurat ist. Wir rationali- sieren diesen Paradigmenwechsel innerhalb einer umfassenden Revision der Licht-Materie Wechselwirkung und indem wir die Verbindung zwischen verschiedenen electronic-structure Methoden und quantenopti- schen Modellen hervorheben. Diese ausführliche Diskussion hebt hervor, dass die Polariton-Konstruktion nicht nur ein mathematischer Trick ist, sondern auf einem einfachen und physikalischem Argument ba- siert: wenn die Anregungen eines Systems einen hybriden Charakter haben, dann ist es nur natürlich, die zugehörige Theorie bezüglich dieser neuen Entitäten zu formulieren. Schließlich diskutieren wir ausführlich, wie Standard-Algorithmen von electronic-structure Methoden angepasst werden müssen, um der neuen Fermi-Bose Statistik gerecht zu werden. Um die zugehörigen nichtlinearen Ungleichungs-Nebenbedingungen zu garantieren, sind sorgfältige Entwicklung, Implemen- tierung und Validierung der numerischen Algorithmen nötig. Diese zusätzliche numerische Komplexität ist der Preis, den wir zahlen, um das gekoppelte Elektron-Photon Problem zugänglich zu first-principles Me- thoden zu machen. iii iv Abstract Recent experimental progress in the field of cavity quantum electrodynamics allows to study the regime of strong interaction between quantized light and complex matter systems. Due to the coherent coupling between photons and matter-degrees of freedom, polaritons – hybrid light-matter quasiparticles – emerge, which can significantly influence matter properties and complex process such as chemical reactions. This strong-coupling regime opens up possibilities to control materials and chemistry in an unprecedented way. However, the precise mechanisms behind many of these phenomena are not yet entirely understood. One important reason is that often the physical problem is described with highly simplified models, where the matter system is reduced to a few effective levels. More accurate first-principles approaches that consider photons on the same footing as electrons only slowly emerge. Their development is hampered by the in- crease of complexity of the combined electron-photon wave functions and the fact that we have to deal with two different species of particles. In this thesis we propose a way to overcome these problems by reformulating the coupled electron- photon problem in an exact way in a different, purpose-build Hilbert space, where no longer electrons and photons are the basic physical entities but the polaritons. Representing an N-electron-M-mode sys- tem by an N-polariton wave function with hybrid Fermi-Bose statistics, we show explicitly how to turn electronic-structure methods into polaritonic-structure methods that are accurate from the weak to the strong-coupling regime. We elucidate this paradigmatic shift by a comprehensive review of light-matter coupling, as well as by highlighting the connection between different electronic-structure methods and quantum-optical models. This extensive discussion accentuates that the polariton description is not only a mathematical trick, but it is grounded in a simple and intuitive physical argument: when the excitations of a system are hybrid entities a formulation of the theory in terms of these new entities is natural. Finally, we discuss in great detail how to adopt standard algorithms of electronic-structure methods to adhere to the new hybrid Fermi-Bose statistics. Guaranteeing the corresponding nonlinear inequality con- straints in practice requires a careful development, implementation and validation of numerical algorithms. This extra numerical complexity is the price we pay for
Load more

Recommended publications
  • Tensor Network Methods in Many-Body Physics Andras Molnar
    Tensor Network Methods in Many-body physics Andras Molnar Ludwig-Maximilians-Universit¨atM¨unchen Max-Planck-Institut f¨urQuanutenoptik M¨unchen2019 Tensor Network Methods in Many-body physics Andras Molnar Dissertation an der Fakult¨atf¨urPhysik der Ludwig{Maximilians{Universit¨at M¨unchen vorgelegt von Andras Molnar aus Budapest M¨unchen, den 25/02/2019 Erstgutachter: Prof. Dr. Jan von Delft Zweitgutachter: Prof. Dr. J. Ignacio Cirac Tag der m¨undlichen Pr¨ufung:3. Mai 2019 Abstract Strongly correlated systems exhibit phenomena { such as high-TC superconductivity or the fractional quantum Hall effect { that are not explicable by classical and semi-classical methods. Moreover, due to the exponential scaling of the associated Hilbert space, solving the proposed model Hamiltonians by brute-force numerical methods is bound to fail. Thus, it is important to develop novel numerical and analytical methods that can explain the physics in this regime. Tensor Network states are quantum many-body states that help to overcome some of these difficulties by defining a family of states that depend only on a small number of parameters. Their use is twofold: they are used as variational ansatzes in numerical algorithms as well as providing a framework to represent a large class of exactly solvable models that are believed to represent all possible phases of matter. The present thesis investigates mathematical properties of these states thus deepening the understanding of how and why Tensor Networks are suitable for the description of quantum many-body systems. It is believed that tensor networks can represent ground states of local Hamiltonians, but how good is this representation? This question is of fundamental importance as variational algorithms based on tensor networks can only perform well if any ground state can be approximated efficiently in such a way.
    [Show full text]
  • Tensor Networks, MERA & 2D MERA ✦ Classify Tensor Network Ansatz According to Its Entanglement Scaling
    Lecture 1: tensor network states (MPS, PEPS & iPEPS, Tree TN, MERA, 2D MERA) Philippe Corboz, Institute for Theoretical Physics, University of Amsterdam i1 i2 i3 i4 i5 i6 i7 i8 i9 i10 i11i12 i13 i14 i15i16 i17 i18 Outline ‣ Lecture 1: tensor network states ✦ Main idea of a tensor network ansatz & area law of the entanglement entropy ✦ MPS, PEPS & iPEPS, Tree tensor networks, MERA & 2D MERA ✦ Classify tensor network ansatz according to its entanglement scaling ‣ Lecture II: tensor network algorithms (iPEPS) ✦ Contraction & Optimization ‣ Lecture III: Fermionic tensor networks ✦ Formalism & applications to the 2D Hubbard model ✦ Other recent progress Motivation: Strongly correlated quantum many-body systems High-Tc Quantum magnetism / Novel phases with superconductivity spin liquids ultra-cold atoms Challenging!tech-faq.com Typically: • No exact analytical solution Accurate and efficient • Mean-field / perturbation theory fails numerical simulations • Exact diagonalization: O(exp(N)) are essential! Quantum Monte Carlo • Main idea: Statistical sampling of the exponentially large configuration space • Computational cost is polynomial in N and not exponential Very powerful for many spin and bosonic systems Quantum Monte Carlo • Main idea: Statistical sampling of the exponentially large configuration space • Computational cost is polynomial in N and not exponential Very powerful for many spin and bosonic systems Example: The Heisenberg model . Sandvik & Evertz, PRB 82 (2010): . H = SiSj system sizes up to 256x256 i,j 65536 ⇥ Hilbert space: 2 Ground state sublattice magn. m =0.30743(1) has Néel order . Quantum Monte Carlo • Main idea: Statistical sampling of the exponentially large configuration space • Computational cost is polynomial in N and not exponential Very powerful for many spin and bosonic systems BUT Quantum Monte Carlo & the negative sign problem Bosons Fermions (e.g.
    [Show full text]
  • Tensor Network State Methods and Applications for Strongly Correlated Quantum Many-Body Systems
    Bildquelle: Universität Innsbruck Tensor Network State Methods and Applications for Strongly Correlated Quantum Many-Body Systems Dissertation zur Erlangung des akademischen Grades Doctor of Philosophy (Ph. D.) eingereicht von Michael Rader, M. Sc. betreut durch Univ.-Prof. Dr. Andreas M. Läuchli an der Fakultät für Mathematik, Informatik und Physik der Universität Innsbruck April 2020 Zusammenfassung Quanten-Vielteilchen-Systeme sind faszinierend: Aufgrund starker Korrelationen, die in die- sen Systemen entstehen können, sind sie für eine Vielzahl an Phänomenen verantwortlich, darunter Hochtemperatur-Supraleitung, den fraktionalen Quanten-Hall-Effekt und Quanten- Spin-Flüssigkeiten. Die numerische Behandlung stark korrelierter Systeme ist aufgrund ih- rer Vielteilchen-Natur und der Hilbertraum-Dimension, die exponentiell mit der Systemgröße wächst, extrem herausfordernd. Tensor-Netzwerk-Zustände sind eine umfangreiche Familie von variationellen Wellenfunktionen, die in der Physik der kondensierten Materie verwendet werden, um dieser Herausforderung zu begegnen. Das allgemeine Ziel dieser Dissertation ist es, Tensor-Netzwerk-Algorithmen auf dem neuesten Stand der Technik für ein- und zweidi- mensionale Systeme zu implementieren, diese sowohl konzeptionell als auch auf technischer Ebene zu verbessern und auf konkrete physikalische Systeme anzuwenden. In dieser Dissertation wird der Tensor-Netzwerk-Formalismus eingeführt und eine ausführ- liche Anleitung zu rechnergestützten Techniken gegeben. Besonderes Augenmerk wird dabei auf die Implementierung
    [Show full text]
  • Continuous Tensor Network States for Quantum Fields
    PHYSICAL REVIEW X 9, 021040 (2019) Featured in Physics Continuous Tensor Network States for Quantum Fields † Antoine Tilloy* and J. Ignacio Cirac Max-Planck-Institut für Quantenoptik, Hans-Kopfermann-Straße 1, 85748 Garching, Germany (Received 3 August 2018; revised manuscript received 12 February 2019; published 28 May 2019) We introduce a new class of states for bosonic quantum fields which extend tensor network states to the continuum and generalize continuous matrix product states to spatial dimensions d ≥ 2.By construction, they are Euclidean invariant and are genuine continuum limits of discrete tensor network states. Admitting both a functional integral and an operator representation, they share the important properties of their discrete counterparts: expressiveness, invariance under gauge transformations, simple rescaling flow, and compact expressions for the N-point functions of local observables. While we discuss mostly the continuous tensor network states extending projected entangled-pair states, we propose a generalization bearing similarities with the continuum multiscale entanglement renormal- ization ansatz. DOI: 10.1103/PhysRevX.9.021040 Subject Areas: Particles and Fields, Quantum Physics, Strongly Correlated Materials I. INTRODUCTION and have helped describe and classify their physical proper- ties. By design, their entanglement obeys the area law Tensor network states (TNSs) provide an efficient para- [17–19], which is a fundamental property of low-energy metrization of physically relevant many-body wave func- states of systems with local interactions. They enable a tions on the lattice [1,2]. Obtained from a contraction of succinct classification of symmetry-protected [20–23] and low-rank tensors on so-called virtual indices, they eco- topological phases of matter [24,25].
    [Show full text]
  • Numerical Continuum Tensor Networks in Two Dimensions
    PHYSICAL REVIEW RESEARCH 3, 023057 (2021) Numerical continuum tensor networks in two dimensions Reza Haghshenas ,* Zhi-Hao Cui , and Garnet Kin-Lic Chan† Division of Chemistry and Chemical Engineering, California Institute of Technology, Pasadena, California 91125, USA (Received 31 August 2020; accepted 31 March 2021; published 19 April 2021) We describe the use of tensor networks to numerically determine wave functions of interacting two- dimensional fermionic models in the continuum limit. We use two different tensor network states: one based on the numerical continuum limit of fermionic projected entangled pair states obtained via a tensor network for- mulation of multigrid and another based on the combination of the fermionic projected entangled pair state with layers of isometric coarse-graining transformations. We first benchmark our approach on the two-dimensional free Fermi gas then proceed to study the two-dimensional interacting Fermi gas with an attractive interaction in the unitary limit, using tensor networks on grids with up to 1000 sites. DOI: 10.1103/PhysRevResearch.3.023057 I. INTRODUCTION and there have been many developments to extend the range of the techniques, for example to long-range Hamiltoni- Understanding the collective behavior of quantum many- ans [15–17], thermal states [18], and real-time dynamics [19]. body systems is a central theme in physics. While it is often Also, much work has been devoted to improving the numeri- discussed using lattice models, there are systems where a cal efficiency and stability of PEPS computations [20–24]. continuum description is essential. One such case is found Formulating tensor network states and the associated algo- in superfluids [1], where recent progress in precise experi- rithms in the continuum remains a challenge.
    [Show full text]
  • Simulating Quantum Computation by Contracting Tensor Networks Abstract
    Simulating quantum computation by contracting tensor networks Igor Markov1 and Yaoyun Shi2 Department of Electrical Engineering and Computer Science The University of Michigan 2260 Hayward Street Ann Arbor, MI 48109-2121, USA E-mail: imarkov shiyy @eecs.umich.edu f j g Abstract The treewidth of a graph is a useful combinatorial measure of how close the graph is to a tree. We prove that a quantum circuit with T gates whose underlying graph has treewidth d can be simulated deterministically in T O(1) exp[O(d)] time, which, in particular, is polynomial in T if d = O(logT). Among many implications, we show efficient simulations for quantum formulas, defined and studied by Yao (Proceedings of the 34th Annual Symposium on Foundations of Computer Science, 352–361, 1993), and for log-depth circuits whose gates apply to nearby qubits only, a natural constraint satisfied by most physical implementations. We also show that one-way quantum computation of Raussendorf and Briegel (Physical Review Letters, 86:5188– 5191, 2001), a universal quantum computation scheme with promising physical implementations, can be efficiently simulated by a randomized algorithm if its quantum resource is derived from a small-treewidth graph. Keywords: Quantum computation, computational complexity, treewidth, tensor network, classical simula- tion, one-way quantum computation. 1Supported in part by NSF 0208959, the DARPA QuIST program and the Air Force Research Laboratory. 2Supported in part by NSF 0323555, 0347078 and 0622033. 1 Introduction The recent interest in quantum circuits is motivated by several complementary considerations. Quantum information processing is rapidly becoming a reality as it allows manipulating matter at unprecedented scale.
    [Show full text]
  • Learning Phase Transition in Ising Model with Tensor-Network Born Machines
    Learning Phase Transition in Ising Model with Tensor-Network Born Machines Ahmadreza Azizi Khadijeh Najafi Department of Physics Department of Physics Virginia Tech Harvard & Caltech Blacksburg, VA Cambridge, MA [email protected] [email protected] Masoud Mohseni Google Ai Venice, CA [email protected] Abstract Learning underlying patterns in unlabeled data with generative models is a chal- lenging task. Inspired by the probabilistic nature of quantum physics, recently, a new generative model known as Born Machine has emerged that represents a joint probability distribution of a given data based on Born probabilities of quantum state. Leveraging on the expressibilty and training power of the tensor networks (TN), we study the capability of Born Machine in learning the patterns in the two- dimensional classical Ising configurations that are obtained from Markov Chain Monte Carlo simulations. The structure of our model is based on Projected Entan- gled Pair State (PEPS) as a two dimensional tensor network. Our results indicate that the Born Machine based on PEPS is capable of learning both magnetization and energy quantities through the phase transitions from disordered into ordered phase in 2D classical Ising model. We also compare learnability of PEPS with another popular tensor network structure Matrix Product State (MPS) and indicate that PEPS model on the 2D Ising configurations significantly outperforms the MPS model. Furthermore, we discuss that PEPS results slightly deviate from the Monte Carlo simulations in the vicinity of the critical point which is due to the emergence of long-range ordering. 1 Introduction In the past years generative models have shown a remarkable progress in learning the probability distribution of the input data and generating new samples accordingly.
    [Show full text]
  • Entanglement and Tensor Network States
    17 Entanglement and Tensor Network States Jens Eisert Freie Universitat¨ Berlin Dahlem Center for Complex Quantum Systems Contents 1 Correlations and entanglement in quantum many-body systems 2 1.1 Quantum many-body systems . 2 1.2 Clustering of correlations . 4 1.3 Entanglement in ground states and area laws . 5 1.4 The notion of the ‘physical corner of Hilbert space’ . 10 2 Matrix product states 11 2.1 Preliminaries . 11 2.2 Definitions and preparations of matrix product states . 13 2.3 Computation of expectation values and numerical techniques . 17 2.4 Parent Hamiltonians, gauge freedom, geometry, and symmetries . 23 2.5 Tools in quantum information theory and quantum state tomography . 27 3 Higher-dimensional tensor network states 29 3.1 Higher-dimensional projected entangled pair states . 29 3.2 Multi-scale entanglement renormalization . 32 4 Fermionic and continuum models 34 4.1 Fermionic models . 34 4.2 Continuum models . 35 E. Pavarini, E. Koch, and U. Schollwock¨ Emergent Phenomena in Correlated Matter Modeling and Simulation Vol. 3 Forschungszentrum Julich,¨ 2013, ISBN 978-3-89336-884-6 http://www.cond-mat.de/events/correl13 17.2 Jens Eisert 1 Correlations and entanglement in quantum many-body systems 1.1 Quantum many-body systems In this chapter we will consider quantum lattice systems as they are ubiquitous in the condensed matter context or in situations that mimic condensed matter systems, as provided, say, by sys- tems of cold atoms in optical lattices. What we mean by a quantum lattice system is that we think that we have an underlying lattice structure given: some lattice that can be captured by a graph.
    [Show full text]
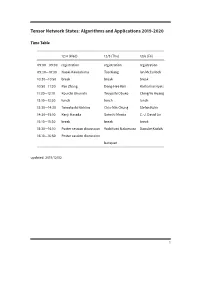
  • Tensor Network States: Algorithms and Applications
    Tensor Network States: Algorithms and Applications 2019-2020 Time Table 12/4 (Wed) 12/5 (Thu) 12/6 (Fri) 09:00—09:30 registration registration registration 09:30—10:30 Naoki Kawashima Tao Xiang Ian McCulloch 10:30—10:50 break break break 10:50—11:30 Pan Zhang Dong-Hee Kim Katharine Hyatt 11:30—12:10 Kouichi Okunishi Tsuyoshi Obuko Ching-Yu Huang 12:10—13:30 lunch lunch lunch 13:30—14:30 Tomotoshi Nishino Chia-Min Chung Stefan Kuhn 14:30—15:10 Kenji Harada Satoshi Morita C.-J. David Lin 15:10—15:30 break break break 15:30—16:10 Poster session discussion Yoshifumi Nakamura Daisuke Kadoh 16:10—16:50 Poster session discussion banquet updated: 2019/12/02 1 Abstracts Day One: 12/4 (Wed) Morning session Chair: Ying-Jer Kao Understanding Kitaev Related Models through Tensor Networks Naoki Kawashima, ISSP, University fo Tokyo I review recent activities related to the Kitaev model and its derivatives. Especially, we devel- oped a new series of tensor network ansatzes that describes the ground state of the Kitaev model with high accuracy. The series of ansatzes suggest the essential similarity between the classical loop gas model and the Kitaev spin liquid. We also use the ansatzes for the initial state for TEBD-type optimization. Approximately contracting arbitrary tensor networks: eicient algorithms and applications in graphical models and quantum circuit simulations Pan Zhang, Institute of Theoretical Physics, Chinese Academy of Sciences Tensor networks are powerful tools in quantum many-body problems, usually defined on lattices where eicient contraction algorithms exist.
    [Show full text]
  • Categorical Tensor Network States
    Categorical Tensor Network States Jacob D. Biamonte,1,2,3,a Stephen R. Clark2,4 and Dieter Jaksch5,4,2 1Oxford University Computing Laboratory, Parks Road Oxford, OX1 3QD, United Kingdom 2Centre for Quantum Technologies, National University of Singapore, 3 Science Drive 2, Singapore 117543, Singapore 3ISI Foundation, Torino Italy 4Keble College, Parks Road, University of Oxford, Oxford OX1 3PG, United Kingdom 5Clarendon Laboratory, Department of Physics, University of Oxford, Oxford OX1 3PU, United Kingdom We examine the use of string diagrams and the mathematics of category theory in the description of quantum states by tensor networks. This approach lead to a unifi- cation of several ideas, as well as several results and methods that have not previously appeared in either side of the literature. Our approach enabled the development of a tensor network framework allowing a solution to the quantum decomposition prob- lem which has several appealing features. Specifically, given an n-body quantum state |ψi, we present a new and general method to factor |ψi into a tensor network of clearly defined building blocks. We use the solution to expose a previously un- known and large class of quantum states which we prove can be sampled efficiently and exactly. This general framework of categorical tensor network states, where a combination of generic and algebraically defined tensors appear, enhances the theory of tensor network states. PACS numbers: 03.65.Fd, 03.65.Ca, 03.65.Aa arXiv:1012.0531v2 [quant-ph] 17 Dec 2011 a [email protected] 2 I. INTRODUCTION Tensor network states have recently emerged from Quantum Information Science as a gen- eral method to simulate quantum systems using classical computers.
    [Show full text]
  • Quantum Quench Dynamics and Entanglement
    © 2018 by Tianci Zhou. All rights reserved. QUANTUM QUENCH DYNAMICS AND ENTANGLEMENT BY TIANCI ZHOU DISSERTATION Submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Physics in the Graduate College of the University of Illinois at Urbana-Champaign, 2018 Urbana, Illinois Doctoral Committee: Assistant Professor Thomas Faulkner, Chair Professor Michael Stone, Director of Research Professor Peter Abbamonte Assistant Professor Lucas Wagner Abstract Quantum quench is a non-equilibrium process where the Hamiltonian is suddenly changed during the quan- tum evolution. The change can be made by spatially local perturbations (local quench) or globally switch- ing to a completely different Hamiltonian (global quench). This thesis investigates the post-quench non- equilibrium dynamics with an emphasis on the time dependence of the quantum entanglement. We inspect the scaling of entanglement entropy (EE) to learn how correlation and entanglement built up in a quench. We begin with two local quench examples. In Chap.2, we apply a local operator to the groundstate of the quantum Lifshitz model and monitor the change of the EE. We find that the entanglement grows according to the dynamical exponent z = 2 and then saturates to the scaling dimension of the perturbing operator { a value representing its strength. In Chap.3, we study the evolution after connecting two different one-dimensional critical chains at their ends. The Loschmidt echo which measures the similarity between the evolved state and the initial one decays with a power law, whose exponent is the scaling dimension of the defect (junction). Among other conclusions, we see that the local quench dynamics contain universal information of the (critical) theory.
    [Show full text]
  • Fermionic Criticality Is Shaped by Fermi Surface Topology: a Case
    Published for SISSA by Springer Received: May 6, 2020 Revised: February 20, 2021 Accepted: March 9, 2021 Published: April 15, 2021 Fermionic criticality is shaped by Fermi surface topology: a case study of the Tomonaga-Luttinger liquid JHEP04(2021)148 Anirban Mukherjee, Siddhartha Patra and Siddhartha Lal Department of Physical Sciences, Indian Institute of Science Education and Research — Kolkata, Mohanpur Campus, West Bengal — 741246, India E-mail: [email protected], [email protected], [email protected] Abstract: We perform a unitary renormalization group (URG) study of the 1D fermionic Hubbard model. The formalism generates a family of effective Hamiltonians and many- body eigenstates arranged holographically across the tensor network from UV to IR. The URG is realized as a quantum circuit, leading to the entanglement holographic mapping (EHM) tensor network description. A topological Θ-term of the projected Hilbert space of the degrees of freedom at the Fermi surface are shown to govern the nature of RG flow towards either the gapless Tomonaga-Luttinger liquid or gapped quantum liquid phases. This results in a nonperturbative version of the Berezenskii-Kosterlitz-Thouless (BKT) RG phase diagram, revealing a line of intermediate coupling stable fixed points, while the nature of RG flow around the critical point is identical to that obtained from the weak-coupling RG analysis. This coincides with a phase transition in the many-particle entanglement, as the entanglement entropy RG flow shows distinct features for the critical and gapped phases depending on the value of the topological Θ-term. We demonstrate the Ryu-Takyanagi entropy bound for the many-body eigenstates comprising the EHM network, concretizing the relation to the holographic duality principle.
    [Show full text]