DOCSLIB.ORG

Hindu Astronomy

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Hindu Astronomy HINDU ASTRONOMY BY W. BRENNAND, WITH THIRTEEN ILLUSTRATIONS AND NUMEROUS DIAGRAMS. London : Published by Chas. Straker & Sons, Ltd., Bishopsgate Avenue, E.C. 1896. S JUL 3 1 1974 fysm OF Wf B-7M Printed by Chas. Straker & Sons, Ltd., BisiiorsoATE Avenue, London, E.G. PREFACE. It is perhaps expected that some reason should be given for tho publication of this work, though it may appear inadequate. Force of circumstances; rather than deliberate choice on my part, impelled it now that it has been I cannot but feel how ; and, accomplished, imperfect the production is. A lengthened residence in India led me to become interested in the study of the ancient mathematical works of the Hindus. This study was frequently interrupted by official duties, and much information acquired in its course lias been for a time forgotten. Recent circumstances, and chiefly the interest displayed by my former pupils in a paper presented to the Royal Society on the same subject, has induced me to make an effort to regain the lost ground, and to gather together materials for a more extended work. Moreover, a conviction formed many years ago that the Hindus have not received the credit due to their literature and mathematical science from Europeans, and which has been strengthened by a renewal of my study of those materials, has led me also to a desire to put before the public their system of astronomy in as simple a maimer as possible, with the object of enabling those interested in the matter to form their own judgment upon it, and, possibly, to extend further investigations in the subject. I have found far greater difficulties than I had anticipated from the fact that, although, no doubt, many Hindu writings exist which, if translated and consulted, would throw greater light upon the matter, yet comparatively few have undergone European investiga- tion. I have been greatly assisted in my endeavours by the follow- ing books, from some of which I have made copious extracts, in order to present the views of others than myself. l*. Preface, " and The works of Sir W. Jones, Bnilly'e Astronomie Indienne," of on in the "Transactions of the Royal Society Playfiurs'i paper it, in Asiatic Researches," Colebrooke's Edinburgh," Davis's "Essays "Hindu mys and Translations from the Sanscrit," Bentle/s Professor Max Muller, Astronomy," references to Captain Wilford, and other the Institutes of Ferguson*! "Architecture," works; Akber, and the translation of the Siddhanta Siromani of Launcelot Wilkinson. I .8. know- f have not entered at greater length into the mathematical char- ledge of the Hindus than will he sufficient to show its general acter, and that it was adequate for their requirements in the ordinary business of their lives, and for the purposes of their astronomy. In the description of the Surya Siddhanta I have been indebted to tin- translation, of this work from the Sanscrit, by Pundit Bapu Dt-va Saatri, of the Sanscrit College of Benares. I take this opportunity of offering my thanks to my former pupils, who, after so many (23) years, still retain their attachment to ine in my retirement, and especially to Rajah Rajendro Narayan of Roy Chowdry Bhowal, who have all taken the greatest interest in the progress of this work. W. BRENNAND. Thi Fort, Milverton, Somerset, 25th March, 1896. CONTENTS PART I. CHAPTER I. PREHISTORIC ASTRONOMY OF THE ARYAN MIGRATING TRIBES. Countries inhabited by Aryan Races. Routes of Migration, East, West and South Alpha Draconis as Polaris 2800 B.C. Regulus, or Alpha Leonis, rising with Sun and Summer Solstice 2280 B.C. Early Religion of Chinese, resembling that of the Hindus. of Astronomical carried to ., t^Similarity Conceptions by Migrating Tribes ' / their new homes. A figures representing the twelve signs connected with Mythology. *lA Similar imaginary forms of the figures implying nearly the same early Mythology. Origin of the Zodiac traced to Prehistoric Nomads. Natural Deductions from heliacal risings of stars. Origin of Sun Dial from observance of shadow cast by tent poles. Reasons for veneration in which the Solar Signs Taurus and Leo were held. ^ Phases of the Moon Synodic Period figures of signs illustrated. Chinese Signs. Conclusion that all Migrating Tribes carried with them similar signs of the Solar Zodiac. v/The Chinese indebted to Hindus for improvements in their Astronomy. Greeks not possessed of the System of Lunar Mansions. Lunar Mansions called Arabian supposed to be derived from the Chaldeans. Contents. s i of Lunar Mansions being the common possession Probability of the System nons. Names of the Arabian Lunar Mansions. Arabic, and Hindu Lunar Mansions. nparison of Egyptian, Chinese, to Asiatic Nations. Cyole of Sixty Years common of a common in the Summary of Characteristics affording evidence origin Astronomy of Asiatic Nations. CHAPTER II. EAELY HINDU PEKIODS. found in their Origin of the Study of Hindu Astronomy to be religious observances. ^ The Necessity for a Calendar. The Science of Astronomy confined to Brahmins. Antiquity and Civilization of the Hindus, as studied by Europeans in the last century. Exaggerated Chronological Dates of most Eastern Nations in some measure accounted for. Evidence of the great Antiquity of Hindu Astronomy afforded by astronomical tables published in 1687 and 1772 A.D. Hailly's "Astronomie Indienno." l'layfair's investigation of Bailly's work. oral Conclusions arrived at by Playfair. The , supposed general conjunction of planets, etc., in 3102 B.C. The Hindu of Theory Epicycles differs in some respects from that of Ptolemy. The Kali Yuga one of several epochs invented to facilitate astronomical calculations. Years of the M iha Yuga and Kalpa. CHAPTER III. T^E HINDU ECLIPTIC. k ription of the Nncphat-as, or Lunar Asterisms. on into twelve Solar and Signs twenty-eight Lunar Constollations. Illustration, oi the with Northern Ecliptic and Southern Yuga-taras. Contents. vii. Other important stars mentioned. j^Names of the twenty-seven Lunar Asterisms, with figures representing them. Table >f Apparent Longitudes and Latitudes of the twenty-seven Yuga- taras. Observations on Phenomena occurring near the Ecliptic-. Eclipses, and their return in succession in periods of every eighteen years and ten or eleven days. the ^/Eclipses supposed, by ignorant, to presage dreadful events. ^-Extracts from Hindu Writings showing that the causes of eclipses were well understood. " " The point marking the origin of Apparent Longitudes. The modern origin fixed when the Vernal Equinox was in the first point of Aswini, or Mesha (ciro. 570 A.D.) " Meaning of the term precession." Methods of determining the date 570 A.D. Date when the Vernal Equinox coincided with the first point of Crittica. Confirmation of such date found by Bentley in the Hindu Allegory of the birth of four planets (15281371 B.C.) Extract from the Varaha-Sanhita, with reference to the date when the Solstitial Colure passed through the first point of Dhanishtha (oir;. 1110 B.C.) CHAPTER IV. THE HINDU MONTHS, etc. v Different Methods of Measuring Time. I Astronomy of the Vedas described in a treatise entitled Jyotisha. for the adjustment of the ancient Hindu Calendar. Birth of Durga (a personification of the year). ^Formation and Names of the Months. Extracts regarding the Months from the Institutes of Menu. Months called, in the Institutes, Daughters of Dacsha (the Ecliptic), and Consorts of Soma (the Moon). Tiii. Contents. to Sir W. Jones. The Lunar Year more ancient than the Solar, according of India. The Lunar Month having a different beginning in different parts Phases of the Moon- Lunar Month*, according to the Puramts. The tame, according to Jyotishicas (Mathematical Astronomers). Names of the Seasons. CHAPTER V. THE RISHIS. Heliacal Hiving of Rcgulus, marking the position of Summer Solstice, 2280 B.C The Rishis Seven Indian Sages, authors of Vedio hymns, etc., translated to the Celestial Sphere, as stars, Alpha to Heta Ursoe Majoris. Meaning of the word "Rishi." Explanation of the motion erroneously ascribed to these stars. " The Line of the Rishis," a fixed great circle. TV Solstitial Colure, as distinct from the Line of the Rishis. Tl.c Annual Rate of Precession determined by ancient Hindu Astronomers hv means of retrogression of Colure from Line of Rishis. An alternative theory adopted by later astronomers, i.e., a hbration of the on each Equinox side of a mean point. Probable origin of the theory of Hbration. "Line of Rishis" fixwl in position, 1590 B.C. CHAPTER VI. THEORY REGARDING THE CAUSE OF THE PLANETAEY MOTIONS. The Sun and Planet, suppoeed to be carried diurnally Westward with the tart by Pravaha (a mighty wind). The irregular motions caused deities by situated at the Apsides and Nodes, or attracting deflecting them. Contents. ix. CHAPTER VII. ARITHMETIC, ALGEBRA, AND GEOMETRY OF THE HINDUS. Opinions of Dr. Peacock regarding antiquity of Hindu Notation. Dr. Hutton's views on origin and history of Algebra, The Earliest Arabian Treatise on Algebra, by Mahomed Ben Musa. The Algebra of Diophantus probably a translation from some ancient Asiatic manuscript. Encouragement of the Alexandrian School of Astronomy, by the Ptolemies. The Lilavati and Vija-Ganita Hindu treatises on Arithmetic and Algebra. Description of these works by Dr. Hutton. (/The Sun Dial. Examples of problems and methods of solution from Algebra of Hindus. CHAPTER VIII. V HINDU ASTRONOMICAL INSTRUMENTS. The Armillary Sphere. The Nadi Valaya. The Ghati, or Clepehydra. The Chakra., or Circle. CHAPTER IX. EARLY HINDU ASTRONOMERS. Distinction between circumstances derived from a consideration of the great Epic Poems of the Hindus, and even of the Vedas and Institutes of Menu, and circumstances connected with purely astronomical deductions. " " " Two Royal Dynasties the Children of the Sun and the Children of the Moon." Rama, the son of Dasaratha, the hero most distinguished by the Hindus.
Load more

Recommended publications
  • Secondary Indian Culture and Heritage
    Culture: An Introduction MODULE - I Understanding Culture Notes 1 CULTURE: AN INTRODUCTION he English word ‘Culture’ is derived from the Latin term ‘cult or cultus’ meaning tilling, or cultivating or refining and worship. In sum it means cultivating and refining Ta thing to such an extent that its end product evokes our admiration and respect. This is practically the same as ‘Sanskriti’ of the Sanskrit language. The term ‘Sanskriti’ has been derived from the root ‘Kri (to do) of Sanskrit language. Three words came from this root ‘Kri; prakriti’ (basic matter or condition), ‘Sanskriti’ (refined matter or condition) and ‘vikriti’ (modified or decayed matter or condition) when ‘prakriti’ or a raw material is refined it becomes ‘Sanskriti’ and when broken or damaged it becomes ‘vikriti’. OBJECTIVES After studying this lesson you will be able to: understand the concept and meaning of culture; establish the relationship between culture and civilization; Establish the link between culture and heritage; discuss the role and impact of culture in human life. 1.1 CONCEPT OF CULTURE Culture is a way of life. The food you eat, the clothes you wear, the language you speak in and the God you worship all are aspects of culture. In very simple terms, we can say that culture is the embodiment of the way in which we think and do things. It is also the things Indian Culture and Heritage Secondary Course 1 MODULE - I Culture: An Introduction Understanding Culture that we have inherited as members of society. All the achievements of human beings as members of social groups can be called culture.
    [Show full text]
  • Assignment-2
    CS19003 : Programming and Data Structures Laboratory Assignment 2 : Conditional Statements in C Date: 13-April-2021 Problem Statement: It has been almost two weeks since Detective Byomkesh Bakshi and his assistant Ajit were being involved to solve a long-standing murder mystery which was rejuvenated by the pair of murders that happened in the city of joy, Kolkata. There must be some clue hidden within, which are yet to be cracked – may be, the dates of murder can give a definitive clue, who knows! Thinking so, Mr. Bakshi was discussing with Ajit about the characteristic of the dates when these murders happen and the last murder date in particular. However, they found out that, in this eastern part of India, often Bengali calendar is followed (which is a lunar calendar as opposed to the solar Gregorian/English calendar that we universally access) for the dates. In Bengali calendar, the names of the months and the number of days within are different than Gregorian/English calendars, which is shown below: Month No. Month Name Days Month No. Month Name Days Month No. Month Name Days 01 Vaisakha 31 05 Bhadra 31 09 Pausha 30 02 Jyeshtha 31 06 Ashwina 31 10 Magha 30 03 Ashadha 31 07 Kartika 30 11 Phalguna 29 / 30* 04 Shraavana 31 08 Agrahayana 30 12 Chaitra 30 * Phalguna has 30 days, if the corresponding year in which it belongs to is a leap-year; otherwise it has 29 days. Now, Mr. Bakshi asked Ajit to figure out the differences in these two dates of the murder according to the Bangali calendar in various forms.
    [Show full text]
  • Download Book
    PANCI! ASIDDIIANTIKA TIIU ASTRONOMICAL WORK V A 11 A II A MI III II A. TI1IC TEXT, KDITKD WITH AN O'llKIINAlj (U)MMKNTAIIY 1"N SANS AND AN KNOIJSII TRANSLATION AND 1NT1K )DUCT1( ) (1. Tll.niAliT, I'll. '!). i I ) I L I J I > i 1. 1 1 1 ) I 1 ) 1 . M A i I A MA LOPA Y A Y A S A K A A V V E rKlNTKJ) l.V K. ,i. LAZ.MUJN ANP CO., AT TISK J!K1M(.!A1. HALL .PUKSS, 11KNAHEH PKEFACE, There Is some reason to fear that the feeling .of any one who may examine in detail this edition and translation of Varaha Mihira's astronomi- cal work will, in the first place, be wonder at the boldness of the editors. I am indeed fully conscious that on the imperfect materials at our disposal an edition in the strict sense of the word cannot be based, and that what we are able to offer at present deserves no other name but that of a first attempt of the to give a o-eneral idea of the contents PanchasiddMntika. It * o c> would, in these circumstances, possibly have been wiser to delay an edition of the work until more correct Manuscripts have been discovered. Two consider- ations, however, in the end induced us no longer to keep back the results, however imperfect, of our long continued endeavours to restore and elucidate the text of the PanchasiddhantikiL In the first place we" were encouraged by the consideration that texts of purely mathematical or astronomical con- tents may, without great disadvantages, be submitted to a much rougher and bolder treatment than texts of other kinds.
    [Show full text]
  • Indian Calendars
    Undergraduate Research Opportunities Programme in Science (UROPS) INDIAN CALENDARS: COMPARING THE SURYA SIDDHANTA AND THE ASTRONOMICAL EPHEMERIS CHIA DAPHNE ASSOCIATE PROFESSOR HELMER ASLAKSEN DEPARTMENT OF MATHEMATICS NATIONAL UNIVERSITY OF SINGAPORE SEMESTER II 2000/2001 1 CONTENT Page Introduction 3 1.Basic facts about astronomy 4 1.1The ecliptic, celestial equator and equinoxes 4 1.2 Precession of the equinoxes 5 1.3 Measuring a solar year 6 2. The workings of the Indian solar and lunisolar calendars 8 2.1 The Indian solar calendars 8 2.1.1 Measuring a solar year 8 2.1.2 Measuring a solar month 9 2.2 The Indian lunisolar calendars 11 2.2.1 The Amanta month 11 2.2.2 Tithi 12 3. The Surya Siddhanta vs the Astronomical Ephemeris 14 3.1 The Surya Siddhanta 14 3.2 The Astronomical Ephemeris 15 4. Computer codes: Algorithms based on ephemeric rules 16 4.1 Fixed day numbers 16 4.1.1 The fixed calendar: R.D. dates 16 4.1.2 Julian day number 18 4.2 Epochs 19 4.2.1 Hindu epoch 19 4.3 The siddhantic and ephemeric codes: A comparison 20 4.3.1 Hindu sidereal year and the Hindu epoch 21 4.3.2 Solar longitude and Hindu solar longitude 21 4.3.3 Lunar longitude and Hindu lunar longitude 28 4.4 Appendix 30 5. References 32 6. Acknowledgements 32 2 Introduction The history of calendars in India is a remarkably complex subject, owing to the continuity of Indian civilization and to the diversity of cultural influences.
    [Show full text]
  • ANSWERED ON:07.12.2015 E-Ticketing for Monuments Mishra Shri Anoop;Rao Shri Rayapati Sambasiva
    GOVERNMENT OF INDIA CULTURE LOK SABHA UNSTARRED QUESTION NO:1352 ANSWERED ON:07.12.2015 E-Ticketing for Monuments Mishra Shri Anoop;Rao Shri Rayapati Sambasiva Will the Minister of CULTURE be pleased to state: GOVERNMENT OF INDIA MINISTRY OF CULTURE LOK SABHA UNSTARRED QUESTION NO.1352 TO BE ANSWERED ON 7.12.2015 AGRAHAYANA 16, 1937 (SAKA) E-TICKETING FOR MONUMENTS +1352. SHRI ANOOP MISHRA: SHRI RAYAPATI SAMBASIVA RAO: Will the Minister of CULTURE be pleased to state: (a) whether the Archaeological Survey of India (ASI) proposes to introduce e-ticketing system for entry into protected monuments in the country; (b) if so, the details thereof and the time by which the said proposal is likely to be implemented; (c) if not, the reasons therefor; (d) whether the Government has taken any steps to increase the revenue from the ticketed monuments in the country; and (e) if so, the details thereof along with the details of revenue generated from each such monument, State-wise and monument-wise? Answer ANSWER MINISTER OF STATE, CULTURE AND TOURISM (INDEPENDENT CHARGE) AND MINISTER OF STATE, CIVIL AVIATION (DR. MAHESH SHARMA) (a)to(c) Yes, Madam. Archaeological Survey of India has launched e-ticketing services at Taj Mahal, Agra and a few monuments of Delhi. E-ticketing services will be launched at all ticketed monuments shortly. (d) Enhancement in entry fee at centrally protected ticketed monuments and charges of license fee for filming operations in the centrally protected monuments have been made vide Gazette Notification No.G.S.R. 607(E) dated 31st July, 2015.
    [Show full text]
  • Calendars and Timelines SYNOPSIS
    Welland Gouldsmith School History worksheet Class 4 Chapter 3- Calendars and Timelines SYNOPSIS: Calendar lists the days ,weeks and months of the year. We use it to plan our activities and stay ​ organised. The calendar we use is called the Gregorian Calendar. It was introduced by Pope Gregory xiii ​ ​ in 1582. It is based on the Earth's movement around the sun. The time the Earth takes to go around the sun once is called a year. One year has 365 days and every fourth year is a leap year. It has 366 days . Saka Calendar- It is India's national calendar. It was introduced in 1957. ​ The Saka Calendar also has 12 months. They are:- Chaitra ,Vaishakha , Jyeshtha, Ashadha ,Shravana, Bhaadra ,Ashwin ,Kartika, Agrahayana, Pausha ,Magha and Phalguna. Similarities between Gregorian and Saka calendar. ​ 1. Both calendars have 365 days in a year and 366 days in a leap year. 2. Both have 12 months in a year. 3. The months in both calendars have 30 / 31 days. Differences between Gregorian and Saka calendar. ​ Gregorian Calendar - January is the first month and December is the last month. It starts from ​ 1st January. It is followed all over the world. Shakha calendar -Chaitra is the first month and Phalguna is the last month. It starts from 21/ 22 ​ March. It is India's national calendar. Timeline - Timeline is used in history because they tell us ​ ● When an event happened. ● What happened before it. ● What happened after it. In history we use BC and AD with years. BC stands for before the birth of Christ.
    [Show full text]
  • Samskruti Jan 2016 Newsletter E Version
    SAMSKRUTI January 2016 January Refining Young Minds FROM THE Our Master’s Voice EDITORS The Preceptor May the entire universe be By Poornimaji blessed with peace and hope. May everyone who is driven Sixteen year old Sadhanawas sitting in the backyard seriously trying to mould some clay. by envy and enmity become Kirtana, Sadhana’sMother, came up to her and asked, “Sadhana! What are you trying to do?” pacified and reconciled. “Ma! I saw Archanaaunty mould some clay into Hanumanji! Am trying too… But it seems so tough! She did it effortlessly.” May all living beings become “Sadhana! Come along with me, let me tell you.” calm by taking the path of Both of them came and sat in the hall and Kirtanacontinued, Bhakti, for by accepting seva “Sadhana, just as you go to a school to learn your subjects, any art has to be learnt from some teacher. It’s the teacher who they will think of each would know the nuances of an art and it is in his guidance and with his blessings that we attain perfection in any art.” other’s welfare. Sadhananodded and asked, May our own hearts and “Is this the same reason why we seek the blessings of a Guru before doing any spiritual activity too ma?” minds be filled with purity Kirtana smilingly nodded and continued, and serenity. May all the above blessings “Yes dear! It is at the Feet of a Guru, that spiritual knowledge dawns. A Guru, tells you the way. Not stopping at it, he warns flow naturally from The you on the pitfalls and saves you from them.
    [Show full text]
  • Histroy of Astrology
    THE HISTORY OF ASTROLOGY THE HISTORY OF ASTROLOGY Astrology consists of a number of belief systems which hold that there is a relationship between visible astronomical phenomena and events in the human world. In the West, astrology most often consists of a system of horoscopes that claim to predict aspects of an individual's personality or life history based on the positions of the sun, moon, and planetary objects at the time of their birth. Many other cultures have attached importance to astronomical events, and the Indian, Chinese, and Mayan cultures developed elaborate systems for predicting terrestrial events from celestial observations. Source : Wikipedia, the free encyclopedia THE HISTORY OF ASTROLOGY Astrology’s origins in Indo-European cultures trace to the third millennium BCE, with roots in calendrical systems used to predict seasonal shifts and to interpret celestial cycles as signs of divine communications. Through most of its history it was considered a scholarly tradition. It was accepted in political and academic contexts, and its concepts were built into other studies, such as astronomy, alchemy, meteorology, and medicine. At the end of the 17th century, new scientific concepts in astronomy (such as heliocentrism) began to damage the credibility of astrology, which subsequently lost its academic and theoretical standing. Astrology saw a popular revival in the 19th and 20th centuries as part of a general revival of spiritualism and later New Age philosophy, and through the influence of mass media such as newspaper horoscopes. ETYMOLOGY The word astrology comes from the Latin astrologia, deriving from the Greek noun αστρολογία , which combines ἄἄἄστρο astro, 'star, celestial body' with λογία logia, 'study of, theory, discourse (about)'.
    [Show full text]
  • 3.3 INDIAN CALENDARS S.K.Chatterjee A-9/1 Vasant Vihar
    3.3 INDIAN CALENDARS S.K.Chatterjee A-9/1 Vasant Vihar, New Delhi 110 057, India. VEDANGA JYAUTISA CALENDAR The first treatise on calendric astronomy was compiled C1300 B.C.and is known as "The Vedahga Jyautisa. It gives rules for framing calendar covering a five-year period, called a 'Yuga' . In this yuga-period calendar, there were 1830 civil days, 60 solar months, 62 synodic lunar months, and 67 sidereal lunar months. The calen­ dar was luni-solar, and the year started from the first day of the bright fortnight when the Sun returned to the Delphini star group. Corrections were made, as required, to maintain this stipulation to the extent possible. The Vedahga calendar was framed on the mean motions of the luminaries, the Sun and the Moon, and was based on approximate values of their periods. Vedanga Jyautisa calendar remained_ in use for a very long time from C 1300 B.C. to C 400 A.D. when Siddhanta Jyautisa calendar based on true positions of the_Sun and the Moon came into use and gradually replaced totally the Vedanga calendar. THE SURYA SIDDHANTA On the dwindling of Vedanga Jyautisa system, many books on Siddhanta Jyautisa appeared, but the best treatise on the subject and also one that is followed now is named as Surya Siddhanta. It is not known who was the author of this famous book, and when it first came into use. It completely replaced the Vedanga Jyautisa calendar which ruled the calendric system of this sub-continent for more than 1500 years. The Surya Siddhanta astronomers devised rules for framing the calendar on the basis of true positions of the Sun and the Moon as against their mean positions used earlier.
    [Show full text]
  • D-Farana. Olin<<UI Agrahayana, As, T, Am
    d-farana. 114 agriidhrlya. a musical instrument n. a. mul- the function of the is, is, m. f, Ved. dngara, am, (fr. angara), where a sacrificial fire is kindled ; A-ghdti, on shaken, a or rattle. firebrands. kindles the sacred fire. which sounds being cymbal titude of priest who am, within the Agnl- 1 m. A'jniJItriya, u*, S, being ^THI ! ii-yliarsha, as, (rt. ghrish), j, ^.. dnyirasa, as, i, am (fr. anyiras), is kindled dhra or the where a sacrificial fire ; or to the place rubbing, friction. descended from or belonging to referring within the ; the m. the fire Agnldhra to m. a descendant of (as), (agnt) A-gharehana, as, i, am, scratching, rubbing; Aivgiiasas or An-giras; (as), within the Agnidhra. n. friction f. a brush, a rubber. a N. of the fire-place (dhishnya) rubbing, ; (I), An-giras ; especially Vrihaspati, preceptor to the (am), as, a, am, belonging Agnidhra brushed. the a will of Brahm5 and AijHlilhrya, A-gharshita, as, d, am, rubbed, of gods ; Kshatriya by by or the who kindles the sacred fire. priest rt. han with profession. Ved. consecrated to -.HI VIM S-ghdta, as, m. (fr. a), Agnewlra, as, I, am, Agm a striker ; am a a wound ; ; beater, as, t, (fr. anyuli, and Indra. striking, blow, killing flljjTrtoli dngulika, or ; a or relating retention of urine ; misfortune, pain slaughter-house, like a Agneya, at, i, am, fiery, belonging q. v.), finger. similar to fire or for animals or victims. consecrated to fire or its deity Agni ; a place killing ^ as, praising aloud, m.
    [Show full text]
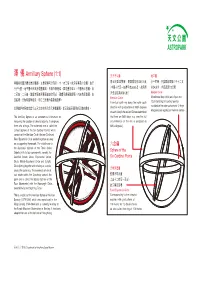
  • Armillary Sphere (1:1)
    ìMň Armillary Sphere (1:1) P7 GɌ Ɍ ìň͈éƼP͵˲ɗňˢľ:C?·XZ#Z9YŹXŹ·:ň%P ˊ9˥ɚƮoŅ=ϝŋ@365¼̑ 8oXƷ=ŋV°PVLc 7 GɌZɌůPʂčͦɌ:5o+βϏľŶƙ˲dz͔\#Ź·Yēň% #ɍD(ƙE ł-·365¼̀ɰŲ S9Ʒ=ŋ?ϟ LɌZL?ɌZͥ˛čͦɌůǩͦɌľ`5̌͵Cūɫƭ˛ƕ9Ź·Vͥň% PRȓƙ·365¼̑ Horizon Circle A horizontal ring with 4 wei, 8 gan and VͥoZPƭů͛Ͳ5CYēň9ūɫƭ˛ƕ Meridian Circle A vertical split ring along the north-south 12 zhi (totalling 24 cardinal points) Fìň͈ȴʙˊĭŁʔP~RɗǺ(=7ìňɒçĦµ̮ʌ"dzGÓɗȜ̑ direction with graduations of 365¼ degrees inscribed on the outer surface and 12 fenye on each side (As the ancient Chinese determined (kingdoms and regions) on the inner surface The Armillary Sphere is an astronomical instrument for that there are 365¼ days in a year, the full measuring the position of celestial objects. It comprises circumference of the sky is assigned as three sets of rings. The outermost one is called the 365¼ degrees) Liuheyi (Sphere of the Six Cardinal Points) which consists of the Meridian Circle, Horizon Circle and Fixed Equatorial Circle welded together securely on a supporting framework. The middle one is :ň the Sanchenyi (Sphere of the Three Stellar Objects) with its four components, namely, the Sphere of the Solstitial Colure Circle, Equinoctial Colure Six Cardinal Points Circle, Mobile Equatorial Circle and Ecliptic Circle joining together and rotating as a whole PʂčͦɌ around the polar axis. The innermost set which can rotate within the Sanchenyi around the .P̸čͦ polar axis is called the Siyouyi (Sphere of the \ŋVLòēEWŋ Four Movements) with the Hour-angle Circle, ̀XWŋo Celestial Axis and Sighting Tube.
    [Show full text]
  • Science in Ancient India
    Science in Ancient India Subhash C. Kak Louisiana State University Baton Rouge, LA 70803-5901, USA November 15, 2005 In Ananya: A portrait of India, S.R. Sridhar and N.K. Mattoo (eds.). AIA: New York, 1997, pages 399-420 1 `Veda' means knowledge. Since we call our earliest period Vedic, this is suggestive of the importance of knowledge and science, as a means of acquiring that knowledge, to that period of Indian history. For quite some time scholars believed that this knowledge amounted to no more than speculations regarding the self; this is what we are still told in some schoolbook accounts. New insights in archaeology, astronomy, history of science and Vedic scholarship have shown that such a view is wrong. We now know that Vedic knowledge embraced physics, mathematics, astronomy, logic, cognition and other disciplines. We ¯nd that Vedic science is the earliest science that has come down to us. This has signi¯cant implications in our understanding of the history of ideas and the evolution of early civilizations. The reconstructions of our earliest science are based not only on the Vedas but also on their appendicies called the Vedangas. The six Vedangas deal with: kalpa, performance of ritual with its basis of geometry, mathematics and calendrics; shiksha, phonetics; chhandas, metrical structures; nirukta, etymology; vyakarana, grammar; and jyotisha, astronomy and other cyclical phenomena. Then there are naturalistic descriptions in the various Vedic books that tell us a lot about scienti¯c ideas of those times. Briefly, the Vedic texts present a tripartite and recursive world view. The universe is viewed as three regions of earth, space, and sky with the corresponding entities of Agni, Indra, and Vishve Devah (all gods).
    [Show full text]