Modeling COVID-19 in Cape Verde Islands - an Application of SIR Model
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Renewable Energy Capacity Statistics 2020
RENEWABLE CAPACITY STATISTICS 2020 STATISTIQUES DE CAPACITÉ RENOUVELABLE 2020 ESTADÍSTICAS DE CAPACIDAD RENOVABLE 2020 www.irena.org Copyright © IRENA 2020 Unless otherwise stated, material in this publication may be freely used, shared, copied, reproduced, printed and/or stored, provided that appropriate acknowledgement is given of IRENA as the source and copyright holder. Material in this publication that is attributed to third parties may be subject to separate terms of use and restrictions, and appropriate permissions from these third parties may need to be secured before any use of such material. ISBN 978-92-9260-239-0 This report should be cited: IRENA (2020), Renewable capacity statistics 2020 International Renewable Energy Agency (IRENA), Abu Dhabi About IRENA The International Renewable Energy Agency (IRENA) is an intergovernmental organisation that supports countries in their transition to a sustainable energy future, and serves as the principal platform for international co-operation, a centre of excellence, and a repository of policy, technology, resource and financial knowledge on renewable energy. IRENA promotes the widespread adoption and sustainable use of all forms of renewable energy, including bioenergy, geothermal, hydropower, ocean, solar and wind energy, in the pursuit of sustainable development, energy access, energy security and low-carbon economic growth and prosperity. www.irena.org Prepared by: Adrian Whiteman, Sonia Rueda, Dennis Akande, Nazik Elhassan, Gerardo Escamilla and Iana Arkhipova. The authors also gratefully acknowledge the contribution to this dataset from national statistical focal points in countries. For further information or to provide feedback, please contact the IRENA Statistics team ([email protected]). This report is available at: www.irena.org/Publications. -

Cape Verde's Infrastructure: a Continental Perspective
COUNTRY REPORT Cape Verde’s Infrastructure: A Continental Perspective Cecilia M. Briceño-Garmendia and Daniel Alberto Benitez AUGUST 2010 © 2010 The International Bank for Reconstruction and Development / The World Bank 1818 H Street, NW Washington, DC 20433 USA Telephone: 202-473-1000 Internet: www.worldbank.org E-mail: [email protected] All rights reserved A publication of the World Bank. The World Bank 1818 H Street, NW Washington, DC 20433 USA The findings, interpretations, and conclusions expressed herein are those of the author(s) and do not necessarily reflect the views of the Executive Directors of the International Bank for Reconstruction and Development / The World Bank or the governments they represent. The World Bank does not guarantee the accuracy of the data included in this work. The boundaries, colors, denominations, and other information shown on any map in this work do not imply any judgment on the part of The World Bank concerning the legal status of any territory or the endorsement or acceptance of such boundaries. Rights and permissions The material in this publication is copyrighted. Copying and/or transmitting portions or all of this work without permission may be a violation of applicable law. The International Bank for Reconstruction and Development / The World Bank encourages dissemination of its work and will normally grant permission to reproduce portions of the work promptly. For permission to photocopy or reprint any part of this work, please send a request with complete information to the Copyright Clearance Center Inc., 222 Rosewood Drive, Danvers, MA 01923 USA; telephone: 978-750-8400; fax: 978-750-4470; Internet: www.copyright.com. -

FINANCIAL CRIME DIGEST April 2021
FINANCIAL CRIME DIGEST April 2021 Diligent analysis. Powering business.™ aperio-intelligence.com FINANCIAL CRIME DIGEST | APRIL 2021 ISSN: 2632-8364 About Us Founded in 2014, Aperio Intelligence is a specialist, independent corporate intelligence frm, headquartered in London. Collectively our team has decades of experience in undertaking complex investigations and intelligence analysis. We speak over twenty languages in- house, including all major European languages, as well as Russian, Arabic, Farsi, Mandarin and Cantonese. We have completed more than 3,000 assignments over the last three years, involving some 150 territories. Our client base includes a broad range of leading international fnancial institutions, law frms and multinationals. Our role is to help identify and understand fnancial crime, contacts, cultivated over decades, who support us regularly integrity and reputational risks, which can arise from a lack in undertaking local enquiries on a confdential and discreet of knowledge of counterparties or local jurisdictions, basis. As a specialist provider of corporate intelligence, we enabling our clients to make better informed decisions. source information and undertake research to the highest legal and ethical standards. Our independence means we Our due diligence practice helps clients comply with anti- avoid potential conficts of interest that can affect larger bribery and corruption, anti-money laundering and other organisations. relevant fnancial crime legislation, such as sanctions compliance, or the evaluation of tax evasion or sanctions We work on a “Client First” basis, founded on a strong risks. Our services support the on-boarding, periodic or commitment to quality control, confdentiality and respect retrospective review of clients or third parties. for time constraints. -

The Cape Verde Jews: an Identity Puzzle
Journal of Cape Verdean Studies Volume 5 Issue 1 Journal of Cape Verdean Studies Fall Article 4 2020 Special Edition On Migration 10-2020 The Cape Verde Jews: an Identity Puzzle Marco Piazza Follow this and additional works at: https://vc.bridgew.edu/jcvs Part of the Critical and Cultural Studies Commons, and the International and Area Studies Commons Recommended Citation Piazza, Marco. (2020). The Cape Verde Jews: an Identity Puzzle. Journal of Cape Verdean Studies, 5(1), 27-35. Available at: https://vc.bridgew.edu/jcvs/vol5/iss1/4 Copyright © 2020 Marco Piazza This item is available as part of Virtual Commons, the open-access institutional repository of Bridgewater State University, Bridgewater, Massachusetts. © 2020 Marco Piazza The Cape Verde Jews: an Identity Puzzle Marco Piazza Department of Philosophy, Communication and Performing Arts Roma Tre University, Italy Abstract The American historian and epistemologist Hayden White said that «there can be no ‘proper history’ which is not at the same time ‘philosophy of history’» (1973, p. XI). But it could also be argued that one cannot make history of philosophy or history of ideas without working on historical data. The data on which I would like to draw attention in this contribution are seemingly reducible to a small thing: they refer to a micro-history that has left few traces, some tombs, surnames, oral memories, and a couple of toponyms. In these pages I will try to show how emblematic this micro-history is to the Cape Verdean identity, the ‘caboverdianidade’ (‘Cape Verdeanness’), and how it can be so concerning identity in general. -

National Strategy for Malaria Elimination in Cape Verde in 2020 Horizon
Research Article Annals of Malaria Research Published: 26 Mar, 2019 National Strategy for Malaria Elimination in Cape Verde in 2020 Horizon Adilson José de Pina1,2*, António Lima Moreira2, Artur Jorge Correia3, Ullardina Domingos Furtado4, Ibrahima Seck5, Ousmane Faye6 and El Hadji Amadou Niang6,7 1Malaria Pre-Elimination Program, CCS-SIDA, Ministry of Health and Social Security, Cabo Verde 2Doctoral School of Life Sciences, Health and Environment (ED-SEV), Cheikh Anta Diop University, Senegal 3National Malaria Control Program and the National Directorate of Health, Ministry of Health and Social Security, Cabo Verde 4Department of Praia Health, Cabo Verde 5Institute of Health and Development, Cheikh Anta Diop University (UCAD), Senegal 6Laboratory of Vector and Parasite Ecology, Cheikh Anta Diop University (UCAD), Senegal 7Aix-Marseille University, IRD, AP-HM, MEPHI, IHU-Mediterranean Infection, France Abstract Malaria continues to be a major public health problem in tropical and subtropical countries. Reduction in morbidity and mortality cases had been reported from 2010 to 2017 in the worldwide. The World Health Organization identified 21 countries with the potential to eliminate malaria by the year 2020, once is Cabo Verde. In the country malaria is instable, with sporadic seasonal transmission variable from year to year and related with the rainy season. From 2010-2016, most of the archipelago malaria cases were imported from African countries and indigenous cases was restricted to Boavista and Santiago islands, especially in Praia, capital city. The outbreak in 2017, with 423 indigenous cases put to the test the weaknesses of the country in the elimination process. Although the feebleness and challenges the country appears that the is one of the best candidates to achieve elimination in the 2020 horizons in the West Africa subregion. -

CAPE VERDE 2021 Annual Research: Key Highlights1
CAPE VERDE 2021 Annual Research: Key Highlights1 Global Data Total GDP contribution: Total Travel & Tourism jobs: 2019 2020 2019 2020 10.4% 5.5% 334MN 272 MN USD 9,170 BN USD 4,671 BN = 1 in 10 jobs =1 in 11 jobs Total Travel & Tourism GDP change in 2020: 1 in 4 net new jobs Change in Jobs in 20202 were created by Travel & -49.1% =USD -4,498 BN Tourism during 2014-2019 Global Economy GDP change: -61.6 MN -3.7% -18.5% Cape Verde Key Data 2019 2020 Total contribution of Travel & Tourism to GDP: -61.9% of Total of Total Change in Travel Economy Economy & Tourism GDP 38.1% 16.2% vs -10.2% real Total T&T GDP = CVE75.6BN Total T&T GDP = CVE28.8BN economy GDP (USD781.4MN) (USD298.0MN) change 2 Total contribution of Travel & Tourism to Employment: Change in jobs : 101.9 67.7 -33.5% Jobs (000s) Jobs (000s) -34.2 (000s) (46.8 % of total employment) (33.4 % of total employment) Change in international visitor Visitor Impact spend: International: CVE56.0BN CVE16.7BN -70.1% Visitor spend Visitor spend -USD 405.7 MN 56.3% of total exports (USD578.7MN) 30.1% of total exports (USD173.0MN) Domestic: Change in domestic visitor spend: CVE6.5BN CVE4.0BN Visitor spend Visitor spend -38.9% (USD 67.6MN) (USD 41.3MN) -USD 26.3 MN CAPE VERDE 2021 Annual Research: Key Highlights1 Cape Verde Sector Characteristics Domestic vs International Spending: Domestic Spending: Domestic Spending: USD 67.6MN (10%) USD 41.3MN (19%) 2019 International Spending: 2020 International Spending: USD 578.7MN (90%) USD 173.0MN (81%) Leisure vs Business Spending: Leisure Spending: Leisure Spending: 2019 USD 582.8MN (90%) 2020 USD 180.5MN (84%) Business Spending: Business Spending: USD 63.6MN (10%) USD 33.9MN (16%) Inbound Arrivals 3: Outbound Departures3 : 2019 2020 2019 2020 1. -

2021 VNR Report Cabo Verde
VOLUNTARY NATIONAL REVIEW ON THE IMPLEMENTATION OF THE 2030 AGENDA FOR SUSTAINABLE DEVELOPMENT 2021 CONTENTS OPENING MESSAGES 5 HIGHLIGHTS 11 EXECUTIVE SUMMARY 15 INTRODUCTION 29 1. 2021 CABO VERDE VNR EXERCISE METHODOLOGY 33 2. POLICIES AND FACILITATING ENVIRONMENT 36 A). INSTITUTIONAL ARRANGEMENTS 36 B). BEST PRACTICE: CABO VERDE - PIONEERING COUNTRY IN THE 38 LOCALIZATION OF THE SDGS C). INVOLVEMENT OF DIFFERENT STAKEHOLDERS IN THE IMPLEMEN- 41 TATION OF THE SDGS D). MECHANISMS TO STRENGTHEN THE ENGAGEMENT AND SUS- TAINABLE PARTICIPATION OF STAKEHOLDERS IN THE PREPARATION, 44 IMPLEMENTATION, MONITORING AND EVALUATION OF PEDS 2022-2026, THE SDGS AND THE STRATEGIC SUSTAINABLE DEVELOPMENT AGENDA E). LEAVE NO ONE BEHIND 45 F). PROGRESS IN IMPLEMENTING THE SDGS 49 SDG 1. ERADICATE POVERTY 50 SDG 2. ERADICATE HUNGER 58 SDG 3. QUALITY HEALTH 64 SDG 4. QUALITY EDUCATION 70 SDG 5. GENDER EQUALITY 78 SDG 6. DRINKING WATER AND SANITATION 84 SDG 7. RENEWABLE AND ACCESSIBLE ENERGY 88 SDG 8. DECENT WORK AND ECONOMIC GROWTH 92 SDG 9. INDUSTRY, INNOVATION AND RESILIENT INFRASTRUCTURE 98 SDG 10. REDUCING INEQUALITIES 102 SDG 11. SUSTAINABLE CITIES AND COMMUNITIES 106 SDG 12. SUSTAINABLE PRODUCTION AND CONSUMPTION 112 CREDITS SDG 13. CLIMATE ACTION 116 National Directorate for Planning, Ministry of Finance, SDG 14. PROTECTING MARINE LIFE 120 Av. Amilcar Cabral, C.P. 30, Praia, Cabo Verde SDG 15. PROTECTING LAND LIFE 126 www.mf.gov.cv The contents may be freely reproduced for non-commercial purposes SDG 16. PEACE, JUSTICE AND EFFECTIVE INSTITUTIONS 132 with attribution to the copyright holders. Maps are not authoritative boundaries. SDG 17. PARTNERSHIPS FOR THE IMPLEMENTATION OF OBJECTIVES 140 Graphic Design and Layout: Alberto Fortes 3. -

Tax Transparency in Africa 2020 Africa Initiative Progress Report: 2019 the Africa Initiative
Tax Transparency in Africa 2020 Africa Initiative Progress Report: 2019 The Africa Initiative Given the high levels of illicit financial flows from African countries and recognising the potential of tax transparency and exchange of information to raise resources for development, African members of the Global Forum on Transparency and Exchange of Information for Tax Purposes attending its plenary meeting on 28 October 2014 in Berlin decided to create an African focused programme: the Africa Initiative. The objective was to unlock the potential of tax transparency and exchange of information for Africa by ensuring that African countries are equipped to exploit the improvements in global transparency to better tackle tax evasion. Focusing on Africa enables the identification of specific approaches and the provision of tailored support to address the specific needs and priorities of African countries to grow their capacity in exchange of information. The Africa Initiative work fits into broader agendas, as tax transparency is an opportunity to stem illicit financial flows and increase domestic resource mobilisation, which are central to the African Union Agenda 2063 and the Sustainable Development Goals. The Africa Initiative was launched as a partnership between the Global Forum, its African members and a number of regional and international organisations and development partners: African Tax Administration Forum, Cercle de Réflexion et d’Echange des Dirigeants des Administrations Fiscales, World Bank Group, France (Ministry of Europe and Foreign Affairs) and the United Kingdom (Department for International Development). Initially set up for a period of three years (2015-2017), the Africa Initiative was renewed for a second phase (2018-2020) in November 2017 at the Global Forum plenary meeting held in Yaoundé, Cameroon. -
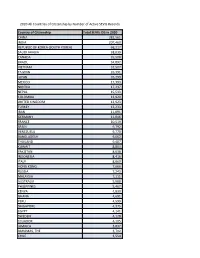
2020 All Countries of Citizenship by Number of Active SEVIS Records
2020 All Countries of Citizenship by Number of Active SEVIS Records Country of Citizenship Total SEVIS IDS in 2020 CHINA 382,561 INDIA 207,460 REPUBLIC OF KOREA (SOUTH KOREA) 68,217 SAUDI ARABIA 38,039 CANADA 35,508 BRAZIL 34,892 VIETNAM 32,507 TAIWAN 26,391 JAPAN 26,299 MEXICO 17,393 NIGERIA 17,237 NEPAL 15,533 COLOMBIA 13,920 UNITED KINGDOM 12,923 TURKEY 12,233 IRAN 11,091 GERMANY 11,046 FRANCE 10,519 SPAIN 9,792 VENEZUELA 9,770 BANGLADESH 9,662 THAILAND 9,487 KUWAIT 8,803 PAKISTAN 8,638 INDONESIA 8,416 ITALY 8,060 HONG KONG 7,666 RUSSIA 7,243 MALAYSIA 7,111 AUSTRALIA 5,688 PHILIPPINES 5,467 KENYA 4,830 GHANA 4,691 PERU 4,599 SINGAPORE 4,375 EGYPT 4,141 SWEDEN 4,128 ECUADOR 4,105 JAMAICA 3,837 BAHAMAS, THE 3,702 CHILE 3,554 SRI LANKA 3,299 MONGOLIA 3,268 JORDAN 3,268 NETHERLANDS 3,266 ARGENTINA 3,174 UKRAINE 3,095 KAZAKHSTAN 3,056 OMAN 3,050 SOUTH AFRICA 2,969 ISRAEL 2,966 ETHIOPIA 2,845 NORWAY 2,837 GREECE 2,628 HONDURAS 2,604 POLAND 2,591 SWITZERLAND 2,543 BURMA 2,322 PANAMA 2,293 DOMINICAN REPUBLIC 2,148 UNITED ARAB EMIRATES 2,113 NEW ZEALAND 2,051 LEBANON 1,845 RWANDA 1,822 MOROCCO 1,801 CONGO (KINSHASA) 1,697 SERBIA 1,688 ZIMBABWE 1,653 COTE D'IVOIRE 1,607 BOLIVIA 1,605 TRINIDAD AND TOBAGO 1,534 COSTA RICA 1,475 BELGIUM 1,468 ALBANIA 1,467 EL SALVADOR 1,459 HAITI 1,417 DENMARK 1,406 GUATEMALA 1,367 PORTUGAL 1,357 IRELAND 1,307 CAMEROON 1,270 ROMANIA 1,181 CZECH REPUBLIC 1,145 AUSTRIA 1,136 TANZANIA 1,105 UGANDA 1,089 CAMBODIA 1,076 ANGOLA 1,067 UZBEKISTAN 1,018 HUNGARY 976 LIBYA 954 QATAR 879 FINLAND 873 BULGARIA 850 TUNISIA 837 -

Iaasars Activity Report 2018
INSTITUTE FOR ASTRONOMY ASTROPHYSICS SPACE APPLICATIONS & REMOTE SENSING NATIONAL OBSERVATORY OF ATHENS IAASARS ACTIVITY REPORT 2018 Yearly Report 2018 IAASARS TABLE OF CONTENTS 1. INTRODUCTION 3 2. SCIENTIFIC FOCUS & CORRESPONDING ACTIVITIES 4 3. STRUCTURE 6 4. RESEARCH ACTIVITIES 10 5. DEVELOPMENT & RESEARCH PROJECTS 44 6. SCIENTIFIC PUBLICATIONS 48 7. RESEARCH COLLABORATIONS 55 8. EDUCATION & PUBLIC OUTREACH 56 9. ACTIVITIES PROMOTING NOA 63 10. SERVICES 69 11. COMMUNICATION 71 2 Yearly Report 2018 IAASARS 1. INTRODUCTION IAASARS is the largest Institute of the National Observatory of Athens. In 2018 it hosted 27 permanent researchers, 5 permanent supporting personnel 27 postdoctoral research associates 32 research support personnel and 20 research students. In addition there were ten adjunct researchers associated to the Institute. The Institute boasts a high scientific productivity as this reflected by the number of publications in international refereed journals. Moreover the Institute has the privilege to host two prestigious European Research Council (ERC) Grants. One on Massive stars (PI A. Bonanos) and the other one on the long-range transport of atmospheric dust (PI V. Amiridis). Additionally, the Institute hosts four major Research Infrastructures: (i) the 2.3-m Aristarchos telescope on Mt. Helmos which currently runs its tenth year of successful operations; (ii) the Kryoneri 1.2-m telescope that has recently been refurbished and has been used continuously ever since - mainly in the framework of the ESA NELIOTA project, monitoring the infall of meteorites on the lunar surface; (iii) the BEYOND center for the monitoring of natural disasters and recently (iv) the PANhellenic GEophysical observatory of Antikythera (PANGEA) which is a major climate change monitoring infrastructure. -

Covid-19 Pandemic: Impact of Restriction Measures in West Africa
Covid -19 Pandemic: Impact of restriction measures In West Africa 1 Acknowledgement This report is the result of close collaboration between the Economic Community of West African States (ECOWAS) Commission, the World Food Programme (WFP), United Nations Economic Commission for Africa (UNECA) and the Economic Commission for Africa (ECA) through its Sub-Regional Office for West Africa. It was developed under the leadership of the ECOWAS Commissioner in charge of Economic Policy and Research, Dr. Kofi Konadu Apraku, the Regional Director of WFP, Mr. Chris Nikoi and the Director of the ECA Sub-regional Office for West Africa, Ms. Ngone Diop. The report was prepared under the supervision and technical coordination of Dr. Simeon Koffi (ECOWAS), Dr. Issa Sanogo (CERFAM), OlloSib (WFP) and Dr. Amadou Diouf (ECA). It benefited from the eminent contributions of Alain Sy Traore (ECOWAS), Marie Ndiaye (WFP), Atsuvi Gamli (WFP), Mariam Katile (WFP), Abdoulaye Ndiaye (WFP), Katrina Frappier (WFP), Dr. Babou Sogue (ECOWAS) and Dr. Silvère Y. Konan (ECA). The online survey component of the report was implemented under the technical coordination of WFP, and supported by WFP Country Office teams and partners from ECOWAS and the ECA. Para Hunzai should also be thanked for logistical support in editing, translating and printing the report. For more information, please contact: Dr. Siméon Koffi, Head of Division, Research and Development, ECOWAS Commission ([email protected]). Dr. Issa Sanogo, CERFAM Director ([email protected]). Ollo Sib, Senior Regional Advisor, Research Assessment and Monitoring, WFP ([email protected]). Dr. Amadou Diouf, CEA/BSR-AO ([email protected]). Table of content 1. -

A SARS-Cov-2 Surveillance System in Sub-Saharan Africa: Modeling Study for Persistence and Transmission to Inform Policy
JOURNAL OF MEDICAL INTERNET RESEARCH Post et al Original Paper A SARS-CoV-2 Surveillance System in Sub-Saharan Africa: Modeling Study for Persistence and Transmission to Inform Policy Lori Ann Post1, PhD; Salem T Argaw2, BA; Cameron Jones3, MPH, MD; Charles B Moss4, PhD; Danielle Resnick5, PhD; Lauren Nadya Singh1, MPH; Robert Leo Murphy6, MD; Chad J Achenbach3, MD; Janine White1, MSc; Tariq Ziad Issa2, BA; Michael J Boctor2, BSc; James Francis Oehmke1, PhD 1Buehler Center for Health Policy & Economics and Departments of Emergency Medicine, Feinberg School of Medicine, Northwestern University, Chicago, IL, United States 2Feinberg School of Medicine, Northwestern University, Chicago, IL, United States 3Division of Infectious Disease, Feinberg School of Medicine, Northwestern University, Chicago, IL, United States 4Institute of Food and Agricultural Sciences, University of Florida, Gainesville, FL, United States 5International Food Policy Research Institute, Washington, DC, United States 6Institute for Global Health, Northwestern University, Chicago, IL, United States Corresponding Author: Lori Ann Post, PhD Buehler Center for Health Policy & Economics and Departments of Emergency Medicine Feinberg School of Medicine Northwestern University 750 N Lake Shore Dr 9th Floor, Suite 9-9035 Rubloff Building Chicago, IL, 60611 United States Phone: 1 203 980 7107 Email: [email protected] Abstract Background: Since the novel coronavirus emerged in late 2019, the scientific and public health community around the world have sought to better understand, surveil, treat, and prevent the disease, COVID-19. In sub-Saharan Africa (SSA), many countries responded aggressively and decisively with lockdown measures and border closures. Such actions may have helped prevent large outbreaks throughout much of the region, though there is substantial variation in caseloads and mortality between nations.