The Community Seismic Network and Quake-Catcher Network: Enabling Structural Health Monitoring Through Instrumentation by Community Participants Monica D
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

A Stake in the Shake: Earthquake Early Warning
A STAKE IN THE SHAKE: EARTHQUAKE EARLY WARNING When an earthquake happens, ShakeAlert STEM Classroom seismic waves travel outward in Discussion: all directions. Primary (P) waves travel faster than How would each of the situations secondary (S) waves and below be made more safe if people S waves do the most and automatic systems were alerted damage. But electronic that they were about to experience information can be sent faster than either wave. earthquake shaking? The ShakeAlert Earth- 1. A surgeon performing an operation. ave you ever felt an earthquake? quake Early Warning System can detect HWhat was it like? Where were you? an earthquake very quickly and send an 2. A chemistry teacher and students What did you do? How are people injured alert of imminent ground motion before working in a lab. during an earthquake? More than 143 mil- strong shaking arrives. 3. A warehouse or construction lion people are exposed to potentially worker. damaging shaking in the United States. The United States Geological Survey (USGS) along with universities and state 4. An amusement park with lots of agencies in Washington, Oregon, fast rides. MATERIALS: Nevada, and California are developing What other places could be made Computer with internet access the ShakeAlert Earthquake Early Warn- ing (EEW) System for the West Coast of safer with earthquake early warning? RESOURCES: the US. Several countries including What can you do to keep yourself ShakeAlert Factsheet (USGS) Japan, Mexico, Taiwan, and China already safe during an earthquake? https://pubs.er.usgs.gov/ -

Dreamplug User Guide GTI-2010.12.10
Quick Start Guide – DreamPlug page 1 / 11 DreamPlug User Guide GTI-2010.12.10 Thank you for purchasing our DreamPlug – The Power to Innovate! This is running at 2.4GHz yet using less than 10W power consumption. This little palm-sized powerhouse can handle all your biggest tasks while still saving about 96% on energy costs when compared to the average 175 Watt desktop computer. You can customize your Plug to work in almost any industry - Cloud ComputingˈHome / Industrial Automation, Security/Surveillance, Medical Monitoring and Data Capture , High End Audio SystemsˈNetwork Storage and monitoring , VoIP and IPPBXˈSmart Grid /Mesh . You can never have enough storage, not to mention fast access to all that data. That's why we have provided Wi-Fi, Bluetooth, Gigabit Ethernet, USB 2.0 and eSATA connection options to the Server line of products. as the AUDIO INTERFACE, the dreamplug can play the music or others data from this port to the external speaker or others devices.in a word, Go ahead give us what you got, we can take it. Package contents DreamPlug Content List Remark 1 DreamPlug 1 unit 2 Detachable AC-DC Power Supply Unit 1 pc 3 Detachable DC-DC Power Cable 1 pc 4 Detachable AC Slider 1 pc 5 Detachable AC Power Cord Adaptor 1 pc 6 AC power Cord 1 pc 7 Protective Slide Cover for DreamPlug 1 pc 8 Protective Slide Cover for Power Supply Unit 1 pc 9 Ethernet Cable 1 pc 10 Warranty Card 1 pc 11 Quick Reference Guide 1 pc 12 External JTAG Debug Module No Optional item. -
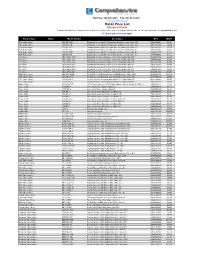
Comprehensiveco.Com Retail Price List Effective 6/15/2018 Pricing Is for Authorized Comprehensive Dealers Only
Toll Free: 800-526-0242 Fax: 201-814-0510 www.comprehensiveco.com Retail Price List Effective 6/15/2018 Pricing is for authorized Comprehensive dealers only. All prices are subject to change without notice. We are not responsible for typographical errors. All terms and conditions apply. Product Type Status Model Number Description UPC MSRP RCA Audio Cables 2PP-2PP-10ST Standard Series 2 gold RCA Plugs Each End Stereo Audio Cable 10ft 808447000016 $8.99 RCA Audio Cables 2PP-2PP-15ST Standard Series 2 gold RCA Plugs Each End Stereo Audio Cable 15ft 808447011760 $10.99 RCA Audio Cables 2PP-2PP-25ST Standard Series 2 gold RCA Plugs Each End Stereo Audio Cable 25ft 808447000047 $11.99 RCA Audio Cables 2PP-2PP-3ST Standard Series 2 gold RCA Plugs Each End Stereo Audio Cable 3ft 808447011913 $3.69 RCA Audio Cables 2PP-2PP-50ST Standard Series 2 gold RCA Plugs Each End Stereo Audio Cable 50ft 808447011777 $22.99 RCA Audio Cables 2PP-2PP-6ST Standard Series 2 gold RCA Plugs Each End Stereo Audio Cable 6ft 808447000092 $6.59 AV Cables 3RCA-3RCA-10ST Standard Series General Purpose 3 RCA Video/Audio Cable 10ft 808447011784 $12.99 AV Cables 3RCA-3RCA-15ST Standard Series General Purpose 3 RCA Video/Audio Cable 15ft 808447049268 $15.99 AV Cables 3RCA-3RCA-25ST Standard Series General Purpose 3 RCA Video/Audio Cable 25ft 808447011791 $19.99 AV Cables 3RCA-3RCA-35ST Standard Series General Purpose 3 RCA Video/Audio Cable 35ft 808447049275 $29.99 AV Cables 3RCA-3RCA-3ST Standard Series General Purpose 3 RCA Video/Audio Cable 3ft 808447011807 $9.99 AV -

AC and Pwr Supply
AC and other line topics ------------------------------------------------------------------------------------------------------------ Date: Sun, 9 Nov 1997 08:02:09 +0500 From: "Chuck Rippel" <crippel@...> Subject: [R-390] Re: Help please GFI problem > Subject: Help please GFI problem > Chuck, you may have once posted suggestions to me or to the reflector > regarding the apparently naturally-ocurring leakage at the line filter > which then trips my GFI in my modern home. I wired in a nice 3-wire > grounded cord and plug to my 390A, and tripped the GFI in the bathroom > adjacent to the shack, taking out the power to the radio. Now, I just am > using a 2-pin adapter at the end of my 3-pin plug, so I've effectively > undone the update I installed. The 390 will not work in a GFI outlet. Wasn't made to pass UL in 1954. > Is there a simple fix to the radio? I'm getting all kinds of > theories from local (well-meaning) ham-friends, but would really > appreciate hearing from you on this. As always, thanks for all your > help. Would like the venerable old radio to be happy in the modern home, > with me the operator safe from annoying "tingles" or worse. I'd put on a 3 wire cord. I do on all the ones I restore. There is actually a military mod for it. It's kinda tricky to make sure you get the polarity right in the input filter tho. The black wire should attach to the terminal on the input network that is TO YOUR >RIGHT< as you face the REAR of the radio. -

Designing the Internet of Things
Designing the Internet of Things Adrian McEwen, Hakim Cassimally This edition first published 2014 © 2014 John Wiley and Sons, Ltd. Registered office John Wiley & Sons Ltd, The Atrium, Southern Gate, Chichester, West Sussex, PO19 8SQ, United Kingdom For details of our global editorial offices, for customer services and for information about how to apply for permission to reuse the copyright material in this book please see our website at www.wiley.com. The right of the author to be identified as the author of this work has been asserted in accordance with the Copyright, Designs and Patents Act 1988. All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording or otherwise, except as permitted by the UK Copyright, Designs and Patents Act 1988, without the prior permission of the publisher. Wiley also publishes its books in a variety of electronic formats. Some content that appears in print may not be available in electronic books. Designations used by companies to distinguish their products are often claimed as trademarks. All brand names and product names used in this book are trade names, service marks, trademarks or registered trademarks of their respective owners. The publisher is not associated with any product or vendor mentioned in this book. This publication is designed to provide accurate and authoritative information in regard to the subject matter covered. It is sold on the under- standing that the publisher is not engaged in rendering professional services. If professional advice or other expert assistance is required, the services of a competent professional should be sought. -

An Earthquake Early Warning System for the West Coast of the United States
Technical Implementation Plan for the ShakeAlert Production System—An Earthquake Early Warning System for the West Coast of the United States Open-File Report 2014–1097 U.S. Department of the Interior U.S. Geological Survey COVER IMAGE: Map generated from the ShakeAlert earthquake early warning system showing the initial 10 seconds of an M7.8 scenario earthquake on the southern San Andreas Fault. Expected warning times for the scenario earthquake are shown by red dashed lines with warning time labeled. Faults (solid dark-gray lines), length of the scenario rupture (dotted black line), and major cities (black dot with city name labeled) are shown. Purple, red, and yellow colors show instantaneous surface velocity of the earthquake, and this data is modified from the TeraShake simulation (www.scec.org/terashake). Technical Implementation Plan for the ShakeAlert Production System—An Earthquake Early Warning System for the West Coast of the United States By D.D. Given, E.S. Cochran, T. Heaton, E. Hauksson, R. Allen, P. Hellweg, J. Vidale, and P. Bodin Open-File Report 2014–1097 U.S. Department of the Interior U.S. Geological Survey U.S. Department of the Interior SALLY JEWELL, Secretary U.S. Geological Survey Suzette M. Kimball, Acting Director U.S. Geological Survey, Reston, Virginia: 2014 For more information on the USGS—the Federal source for science about the Earth, its natural and living resources, natural hazards, and the environment—visit http://www.usgs.gov or call 1–888–ASK–USGS For an overview of USGS information products, including maps, imagery, and publications, visit http://www.usgs.gov/pubprod To order this and other USGS information products, visit http://store.usgs.gov Suggested citation: Given, D.D., Cochran, E.S., Heaton, T., Hauksson, E., Allen, R., Hellweg, P., Vidale, J., and Bodin, P., 2014, Technical implementation plan for the ShakeAlert production system—An Earthquake Early Warning system for the West Coast of the United States: U.S. -

Keyword Rank Create Your Own Proxy Server 1 Alter a Pdf 1 How Do I Find
Keyword Rank create your own proxy server 1 alter a pdf 1 how do i find out the name of a song 1 how to get around blocked youtube videos 1 what version of windows 7 should i buy 1 setting up proxy 1 finding similar songs 1 app store returns 1 youtube music finder 1 google earth picture date 1 wireless mouse freezes 1 use second router as access point 1 set up a proxy 1 second router as access point 1 how to find newspaper articles from the past 1 google voice india number 1 connect two wireless routers together 1 setup a proxy 1 youtube blocked in your country 1 youtube blocked in country 1 youtube playlist on ipad 1 best pdf organizer 1 set up proxy 1 types of computer cords 1 set up second router 1 translate japanese pdf to english 1 computer plugs and connectors 1 how to find news articles from the past 1 compose html email in gmail 1 computer cable names 1 connecting two wireless routers together 1 how to look someone up by email 1 jpeg versus png 1 gmail mailmerge 1 find someone via email 1 remove nyt cookies 1 ipad youtube playlist 1 how to install proxy server 1 how to make a wireless router 1 how to search someone by email 1 edit current website 1 transfer from blogger to wordpress 1 best free dictation software 1 see passwords 1 100 most useful websites 1 how to find high resolution images 1 can you ping an email address 1 pdf file organizer 1 101 websites 1 how can i find out the name of a song 1 websites when your bored 1 how to find a newspaper article from the past 1 return apps 1 how to get old newspaper articles 1 track -

Exploring Perceptions of Shakealert During the 2019 Ridgecrest Earthquake Sequence
Failure to alert? Exploring perceptions of ShakeAlert during the 2019 Ridgecrest Earthquake Sequence Sara K. McBride, Ph.D. Social Science Research Coordinator – ShakeAlert Project Earthquake Science Center U.S. Geological Survey Jeannette Sutton2, Michele Marie Wood3, Lori Peek4, Robert M de Groot5, Andrea L Llenos6, Grace Alexandra Parker7, Danielle F Sumy8, Douglas D Given9, Pascal Schuback10, Ryan Arba11, Rachel Sierer- Co-Authors Wooden11, Emily Holland11, Holly Porter12, Candice Hadley12, Darius Fattahipour12, Alex Bell13 and Gabe Kearney14 1)U.S. Geological Survey, Earthquake Science Center, Kennewick, SPECIAL THANKS TO JASON United States, (2)University of Kentucky, Department of BAUMGARTNER, PUSHSHIFT Communication, Lexington, KY, United States, (3)California State University Fullerton, Fullerton, CA, United States, (4)University of Colorado Boulder, Sociology and Natural Hazards Center, Boulder, CO, United States, (5)United States Geological Survey - Earthquake Science Center, ShakeAlert Project, Pasadena, CA, United States, (6)USGS California Water Science Center Menlo Park, Menlo Park, CA, United States, (7)University of California Los Angeles, Los Angeles, CA, United States, (8)University of Southern California, Los Angeles, CA, United States, (9)USGS, Pasadena, CA, United States, (10)Cascadia Region Earthquake Workgroup, Seattle, United States, (11)California Office of Emergency Services, Sacramento, United States, (12)San Diego Office of Emergency Services, San Diego, United States, (13)San Diego Office of Emergency Services, -

Debian 1 Debian
Debian 1 Debian Debian Part of the Unix-like family Debian 7.0 (Wheezy) with GNOME 3 Company / developer Debian Project Working state Current Source model Open-source Initial release September 15, 1993 [1] Latest release 7.5 (Wheezy) (April 26, 2014) [±] [2] Latest preview 8.0 (Jessie) (perpetual beta) [±] Available in 73 languages Update method APT (several front-ends available) Package manager dpkg Supported platforms IA-32, x86-64, PowerPC, SPARC, ARM, MIPS, S390 Kernel type Monolithic: Linux, kFreeBSD Micro: Hurd (unofficial) Userland GNU Default user interface GNOME License Free software (mainly GPL). Proprietary software in a non-default area. [3] Official website www.debian.org Debian (/ˈdɛbiən/) is an operating system composed of free software mostly carrying the GNU General Public License, and developed by an Internet collaboration of volunteers aligned with the Debian Project. It is one of the most popular Linux distributions for personal computers and network servers, and has been used as a base for other Linux distributions. Debian 2 Debian was announced in 1993 by Ian Murdock, and the first stable release was made in 1996. The development is carried out by a team of volunteers guided by a project leader and three foundational documents. New distributions are updated continually and the next candidate is released after a time-based freeze. As one of the earliest distributions in Linux's history, Debian was envisioned to be developed openly in the spirit of Linux and GNU. This vision drew the attention and support of the Free Software Foundation, who sponsored the project for the first part of its life. -

Cloud Computing – a Simple Explanation
Cloud Computing – a simple Explanation Jere Minich Program Director Lake-Sumter Computer Society Leesburg, Florida 1 Overview for today • 1. What is Cloud Computing.? ( acronym = CC) • 2. Strengths & Free CC. • 3. Why Business Needs CC.? • 4. Types of CC. • 5. How CC works.? • 6. Positive/Advantage of CC. • 7. What is CC like.? • 8. Access, Security, Privacy, Public Records. • 9. CC & Me; Service & Infrastructure • 10 Benefits • 11. A look into the future – Google, Ajax, Mobile, BYOD. 42 –Slides-most- Black & White – Available as: Power Point 2007, PDF, Wordpad. 2 Cloud Computing concept background with a lot of icons: tablet, smartphone, computer, desktop, monitor, music, downloads and so on 3 Cloud Computing Complex 4 Inside Look 5 A view of the Microsoft data center in Dublin, Ireland. 6 Another view of the Microsoft data center in Dublin, Ireland. 7 Cloud computing is where: • software applications, • processing power, • Data • or artificial intelligence are accessed over the Internet. 8 Cloud computing is: • the ability to employ a number of: – computers, – hardware, – software, – and servers - a computer program running to serve the requests of other programs, • to serve your computing needs remotely – without actually owning or running the software and hardware. 9 Cloud computing is: • A much-needed technology that provides: – resources over the Internet, –which are: • extremely accessible • and informative as a service • to those who use Cloud Computing. 10 The strength of cloud computing is: • that it is instantly scalable; – in other words: – more computers can be; • added to • or removed from – the cloud at any time, – without impacting the operation of the cloud. -

Earthquake Early Warning LIVE In
Earthquake Early Warning LIVE in WA! What is ShakeAlert® Earthquake Early Warning? The ShakeAlert® Earthquake Early Warning system is now live in Washington! The system, operated by the U.S. Geological Survey, detects earthquakes that have already begun, rapidly estimates the shaking they will create, then sends an alert to areas which will receive shaking. Seconds of warning can give people time to take action to protect themselves before shaking arrives such as DROP, COVER, and HOLD ON! The system was tested in select counties in Washington in February 2021 and went live on Tuesday, May 4, 2021. How can I get alerts? There are multiple ways you can get alerts on your mobile phone if shaking from an earthquake is expected at your location in WA: through Wireless Emergency Alerts and your phone’s built-in software (no app is required for download). Other third- party mobile applications may be available at a later date. Check below and visit mil.wa.gov/alerts to learn more! How to get alerts on Apple iPhones To check if Wireless Emergency Alerts are turned on for Apple iPhones, you will need to do the following: • Tap “Settings” > “Notifications.” • Scroll to the bottom of the screen. • Under “Government Alerts” tap “Emergency Alerts” and “Public Safety Alerts” to turn them on. How to get alerts on Android Phones To check if Wireless Emergency Alerts are turned on for Android Phones, you will need to do the following: • We recommend that you use the search function in “Settings” to find “Emergency Alerts” or “public safety messages." You may have to click the three dots in the upper right-hand corner of the screen, click settings and click alert types. -

800-526-0242 Fax: 201-814-0510 Effective 6/15/2018 All Terms and Conditions Apply
Toll Free: 800-526-0242 Fax: 201-814-0510 www.comprehensiveco.com Effective 6/15/2018 All terms and conditions apply. Product Type Model Number Description UPC MSRP RCA Audio Cables 2PP-2PP-10ST Standard Series 2 gold RCA Plugs Each End Stereo Audio Cable 10ft 808447000016 $8.99 RCA Audio Cables 2PP-2PP-15ST Standard Series 2 gold RCA Plugs Each End Stereo Audio Cable 15ft 808447011760 $10.99 RCA Audio Cables 2PP-2PP-25ST Standard Series 2 gold RCA Plugs Each End Stereo Audio Cable 25ft 808447000047 $11.99 RCA Audio Cables 2PP-2PP-3ST Standard Series 2 gold RCA Plugs Each End Stereo Audio Cable 3ft 808447011913 $3.69 RCA Audio Cables 2PP-2PP-50ST Standard Series 2 gold RCA Plugs Each End Stereo Audio Cable 50ft 808447011777 $22.99 RCA Audio Cables 2PP-2PP-6ST Standard Series 2 gold RCA Plugs Each End Stereo Audio Cable 6ft 808447000092 $6.59 AV Cables 3RCA-3RCA-10ST Standard Series General Purpose 3 RCA Video/Audio Cable 10ft 808447011784 $12.99 AV Cables 3RCA-3RCA-15ST Standard Series General Purpose 3 RCA Video/Audio Cable 15ft 808447049268 $15.99 AV Cables 3RCA-3RCA-25ST Standard Series General Purpose 3 RCA Video/Audio Cable 25ft 808447011791 $19.99 AV Cables 3RCA-3RCA-35ST Standard Series General Purpose 3 RCA Video/Audio Cable 35ft 808447049275 $29.99 AV Cables 3RCA-3RCA-3ST Standard Series General Purpose 3 RCA Video/Audio Cable 3ft 808447011807 $9.99 AV Cables 3RCA-3RCA-50ST Standard Series General Purpose 3 RCA Video/Audio Cable 50ft 808447012316 $39.99 AV Cables 3RCA-3RCA-6ST Standard Series General Purpose 3 RCA Video/Audio