DOCSLIB.ORG

Development of Trigonometry Medieval Times Serge G

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Development of Trigonometry Medieval Times Serge G Development of trigonometry Medieval times Serge G. Kruk/Laszl´ o´ Liptak´ Oakland University Development of trigonometry Medieval times – p.1/27 Indian Trigonometry • Work based on Hipparchus, not Ptolemy • Tables of “sines” (half chords of twice the angle) • Still depends on radius 3◦ • Smallest angle in table is 3 4 . Why? R sine( α ) α Development of trigonometry Medieval times – p.2/27 Indian Trigonometry 3◦ • Increment in table is h = 3 4 • The “first” sine is 3◦ 3◦ s = sine 3 = 3438 sin 3 = 225 1 4 · 4 1◦ • Other sines s2 = sine(72 ), . Sine differences D = s s • 1 2 − 1 • Second-order approximation techniques sine(xi + θ) = θ θ2 sine(x ) + (D +D ) (D D ) i 2h i i+1 − 2h2 i − i+1 Development of trigonometry Medieval times – p.3/27 Etymology of “Sine” How words get invented! • Sanskrit jya-ardha (Half-chord) • Abbreviated as jya or jiva • Translated phonetically into arabic jiba • Written (without vowels) as jb • Mis-interpreted later as jaib (bosom or breast) • Translated into latin as sinus (think sinuous) • Into English as sine Development of trigonometry Medieval times – p.4/27 Arabic Trigonometry • Based on Ptolemy • Used both crd and sine, eventually only sine • The “sine of the complement” (clearly cosine) • No negative numbers; only for arcs up to 90◦ • For larger arcs, the “versine”: (According to Katz) versine α = R + R sine(α 90◦) − Development of trigonometry Medieval times – p.5/27 Other trig “functions” Al-B¯ırun¯ ¯ı: Exhaustive Treatise on Shadows • The shadow of a gnomon (cotangent) • The hypothenuse of the shadow (cosecant) • The reverse shadow (tangent) • The hypothenuse of the reverse shadow (secant) sun sun reverse shadow shadow Development of trigonometry Medieval times – p.6/27 Height and distance via sine Al-Qab¯ıs¯ı: • Given α1; α2; d • (angles via astrolabe) • find x; y using only sines A y E α1 α2 C d D B x Development of trigonometry Medieval times – p.7/27 Height and distance via sine d sin α y = 2 sin(90◦ α1) sin α2 sin(90◦ α2) − − − sin α1 y sin(90◦ α ) x = − 1 sin α1 Development of trigonometry Medieval times – p.8/27 Arabic Trigonometry • Many trig identities • “Formal” development • Both plane and spherical trig Development of trigonometry Medieval times – p.9/27 Regiomontanus 1436–1476 • Real name Johannes Müller • Translated Ptolemy • Re-did Ptolemy from basic axioms (à la Euclid) • Plane and spherical trig • Many results based on arabic texts Development of trigonometry Medieval times – p.10/27 Later works • Tables of all trig functions n • Based on larger and larger radii (10 ) • . for accuracy • . no good notation for decimals Development of trigonometry Medieval times – p.11/27 Names for trig functions • Regiomontanus 1436–1476: On Triangles of Every Kind • Sinus complementi • Joachim Rheticus 1514–1574 • Trig functions from triangles, no circles! • Thomas Fincke 1561–1656 • Invented words “tangent” and “secant” • Bartholomeo Pitiscus 1561–1613 • Invents the word “Trigonometry” Everything still depends on a particular radius Development of trigonometry Medieval times – p.12/27 Pitiscus's front page Development of trigonometry Medieval times – p.13/27 From • A Gentle History for Teachers and Others • by Berlinghoff and Gouvêa Development of trigonometry Medieval times – p.14/27 Versine • Isaac Newton's Principia 1713 • Charles Hutton A course in Mathematics 1801 • Sine: The line drawn from one extremity of an arc to the diameter, perpendicular to the diameter. • Versed sine: Part of the diameter intercepted between an arc and its sine. R sine( α ) α versine( α ) Development of trigonometry Medieval times – p.15/27 Why tangent? Why secant? Similar triangles (Circle of radius R = 1) a c tan α = = and c is tangent b R R d sec α = = and d is secant b R d R c a α b R Development of trigonometry Medieval times – p.16/27 Napier 1614 • Our notation for decimals • Logs to simplify trig calculations • (Replacing multiplication of sines by addition) Development of trigonometry Medieval times – p.17/27 Leibniz (1693) and sine • Consider a unit circle • Let x = sin y dt dy dx 1 y x Development of trigonometry Medieval times – p.18/27 x = sin y • By similar triangles (because dy is tangent) dt x = dx p1 x2 − • By right angle triangle dx2 + dt2 = dy2 • Isolate dt from second, sub into first, square (1 x2)(dy2 dx2) = x2dx2 − − dy2 = x2dy2 + dx2 Development of trigonometry Medieval times – p.19/27 dy2 = x2dy2 + dx2 • Differential, assume dy constant 0 = d(x2dy2 + dx2) = 2 d(x dy) x dy + 2 d(dx) dx 2 2 = 2xdy(dx dy + x d y) +2 dx dx = 2 dx(d2x + x dy2) • Therefore d2x = x dy2 − Development of trigonometry Medieval times – p.20/27 2 d x = x dy2 − • Since sin is an odd function • and since sin 0 = 0 • Liebniz assumes a power series x = y + cy3 + ey5 + fy7 + : : : • Differentiate twice d2x = 3 2cy + 5 4ey3 + 7 6fy5 + : : : dy2 · · · • Equate term by term both series Development of trigonometry Medieval times – p.21/27 x = sin y • Finally 1 1 x = sin y = y y3 + y5 : : : − 3! 5! − • An expression for sin free of the circle Development of trigonometry Medieval times – p.22/27 Euler 1730 • Power expansion of exponentials and log • Power expansion of sine and cosines • States matter-of-factly a unit circle • And relations between all of them • Trig function really as “functions” • (For Euler, that means analytic) Development of trigonometry Medieval times – p.23/27 Euler: Unification iθ iθ e = cos θ + i sin θ e− = cos θ i sin θ − iθ iθ iθ iθ e e− e + e− sin θ = − cos θ = 2i 2 θ θ θ θ e e− e + e− sinh θ = − cosh θ = 2 2 Name due to Lambert : “Hyperbolic trig functions” Development of trigonometry Medieval times – p.24/27 Why Hyperbolic ? cosh(a) x^2−y^2 = 1 sinh(a) 1 Development of trigonometry Medieval times – p.25/27 Hyperbolic trig sinh θ tanh θ = cosh θ cosh θ coth θ = sinh θ 1 sec hθ = cosh θ 1 csc hθ = sinh θ Verify cosh2θ sinh2θ = 1 − Development of trigonometry Medieval times – p.26/27 Trig: the big picture • Original concept: chords (depends on radius) • Use: Solving triangles (plane and spherical) • Middle-age “sine”: half-chord of double angle • Liebniz and Euler: Unit circle • Euler: trig as proper functions • One Family: exponentials, logs, trig, hyperbolics Discussion: What is a definition for a mathematician? Development of trigonometry Medieval times – p.27/27.
Load more

Recommended publications
  • Unit Circle Trigonometry
    UNIT CIRCLE TRIGONOMETRY The Unit Circle is the circle centered at the origin with radius 1 unit (hence, the “unit” circle). The equation of this circle is xy22+ =1. A diagram of the unit circle is shown below: y xy22+ = 1 1 x -2 -1 1 2 -1 -2 We have previously applied trigonometry to triangles that were drawn with no reference to any coordinate system. Because the radius of the unit circle is 1, we will see that it provides a convenient framework within which we can apply trigonometry to the coordinate plane. Drawing Angles in Standard Position We will first learn how angles are drawn within the coordinate plane. An angle is said to be in standard position if the vertex of the angle is at (0, 0) and the initial side of the angle lies along the positive x-axis. If the angle measure is positive, then the angle has been created by a counterclockwise rotation from the initial to the terminal side. If the angle measure is negative, then the angle has been created by a clockwise rotation from the initial to the terminal side. θ in standard position, where θ is positive: θ in standard position, where θ is negative: y y Terminal side θ Initial side x x Initial side θ Terminal side Unit Circle Trigonometry Drawing Angles in Standard Position Examples The following angles are drawn in standard position: y y 1. θ = 40D 2. θ =160D θ θ x x y 3. θ =−320D Notice that the terminal sides in examples 1 and 3 are in the same position, but they do not represent the same angle (because x the amount and direction of the rotation θ in each is different).
    [Show full text]
  • Trigonometry and Spherical Astronomy 1. Sines and Chords
    CHAPTER TWO TRIGONOMETRY AND SPHERICAL ASTRONOMY 1. Sines and Chords In Almagest I.11 Ptolemy displayed a table of chords, the construction of which is explained in the previous chapter. The chord of a central angle α in a circle is the segment subtended by that angle α. If the radius of the circle (the “norm” of the table) is taken as 60 units, the chord can be expressed by means of the modern sine function: crd α = 120 · sin (α/2). In Ptolemy’s table (Toomer 1984, pp. 57–60), the argument, α, is given at intervals of ½° from ½° to 180°. Columns II and III display the chord, in units, minutes, and seconds of a unit, and the increase, in the same units, in crd α corresponding to an increase of one minute in α, computed by taking 1/30 of the difference between successive entries in column II (Aaboe 1964, pp. 101–125). For an insightful account on Ptolemy’s chord table, see Van Brummelen 2009, where many issues underlying the tables for trigonometry and spherical astronomy are addressed. By contrast, al-Khwārizmī’s zij originally had a table of sines for integer degrees with a norm of 150 (Neugebauer 1962a, p. 104) that has uniquely survived in manuscripts associated with the Toledan Tables (Toomer 1968, p. 27; F. S. Pedersen 2002, pp. 946–952). The corresponding table in al-Battānī’s zij displays the sine of the argu- ment at intervals of ½° with a norm of 60 (Nallino 1903–1907, 2:55– 56). This table is reproduced, essentially unchanged, in the Toledan Tables (Toomer 1968, p.
    [Show full text]
  • Notes on Curves for Railways
    NOTES ON CURVES FOR RAILWAYS BY V B SOOD PROFESSOR BRIDGES INDIAN RAILWAYS INSTITUTE OF CIVIL ENGINEERING PUNE- 411001 Notes on —Curves“ Dated 040809 1 COMMONLY USED TERMS IN THE BOOK BG Broad Gauge track, 1676 mm gauge MG Meter Gauge track, 1000 mm gauge NG Narrow Gauge track, 762 mm or 610 mm gauge G Dynamic Gauge or center to center of the running rails, 1750 mm for BG and 1080 mm for MG g Acceleration due to gravity, 9.81 m/sec2 KMPH Speed in Kilometers Per Hour m/sec Speed in metres per second m/sec2 Acceleration in metre per second square m Length or distance in metres cm Length or distance in centimetres mm Length or distance in millimetres D Degree of curve R Radius of curve Ca Actual Cant or superelevation provided Cd Cant Deficiency Cex Cant Excess Camax Maximum actual Cant or superelevation permissible Cdmax Maximum Cant Deficiency permissible Cexmax Maximum Cant Excess permissible Veq Equilibrium Speed Vg Booked speed of goods trains Vmax Maximum speed permissible on the curve BG SOD Indian Railways Schedule of Dimensions 1676 mm Gauge, Revised 2004 IR Indian Railways IRPWM Indian Railways Permanent Way Manual second reprint 2004 IRTMM Indian railways Track Machines Manual , March 2000 LWR Manual Manual of Instructions on Long Welded Rails, 1996 Notes on —Curves“ Dated 040809 2 PWI Permanent Way Inspector, Refers to Senior Section Engineer, Section Engineer or Junior Engineer looking after the Permanent Way or Track on Indian railways. The term may also include the Permanent Way Supervisor/ Gang Mate etc who might look after the maintenance work in the track.
    [Show full text]
  • Trigonometric Functions
    Hy po e te t n C i u s se o b a p p O θ A c B Adjacent Math 1060 ~ Trigonometry 4 The Six Trigonometric Functions Learning Objectives In this section you will: • Determine the values of the six trigonometric functions from the coordinates of a point on the Unit Circle. • Learn and apply the reciprocal and quotient identities. • Learn and apply the Generalized Reference Angle Theorem. • Find angles that satisfy trigonometric function equations. The Trigonometric Functions In addition to the sine and cosine functions, there are four more. Trigonometric Functions: y Ex 1: Assume � is in this picture. P(cos(�), sin(�)) Find the six trigonometric functions of �. x 1 1 Ex 2: Determine the tangent values for the first quadrant and each of the quadrant angles on this Unit Circle. Reciprocal and Quotient Identities Ex 3: Find the indicated value, if it exists. a) sec 30º b) csc c) cot (2) d) tan �, where � is any angle coterminal with 270 º. e) cos �, where csc � = -2 and < � < . f) sin �, where tan � = and � is in Q III. 2 Generalized Reference Angle Theorem The values of the trigonometric functions of an angle, if they exist, are the same, up to a sign, as the corresponding trigonometric functions of the reference angle. More specifically, if α is the reference angle for θ, then cos θ = ± cos α, sin θ = ± sin α. The sign, + or –, is determined by the quadrant in which the terminal side of θ lies. Ex 4: Determine the reference angle for each of these. Then state the cosine and sine and tangent of each.
    [Show full text]
  • 4.2 – Trigonometric Functions: the Unit Circle
    Warm Up Warm Up 1 The hypotenuse of a 45◦ − 45◦ − 90◦ triangle is 1 unit in length. What is the measure of each of the other two sides of the triangle? 2 The hypotenuse of a 30◦ − 60◦ − 90◦ triangle is 1 unit in length. What is the measure of each of the other two sides of the triangle? Pre-Calculus 4.2 { Trig Func: The Unit Circle Mr. Niedert 1 / 27 4.2 { Trigonometric Functions: The Unit Circle Pre-Calculus Mr. Niedert Pre-Calculus 4.2 { Trig Func: The Unit Circle Mr. Niedert 2 / 27 2 Trigonometric Functions 3 Domain and Period of Sine and Cosine 4 Evaluating Trigonometric Functions with a Calculator 4.2 { Trigonometric Functions: The Unit Circle 1 The Unit Circle Pre-Calculus 4.2 { Trig Func: The Unit Circle Mr. Niedert 3 / 27 3 Domain and Period of Sine and Cosine 4 Evaluating Trigonometric Functions with a Calculator 4.2 { Trigonometric Functions: The Unit Circle 1 The Unit Circle 2 Trigonometric Functions Pre-Calculus 4.2 { Trig Func: The Unit Circle Mr. Niedert 3 / 27 4 Evaluating Trigonometric Functions with a Calculator 4.2 { Trigonometric Functions: The Unit Circle 1 The Unit Circle 2 Trigonometric Functions 3 Domain and Period of Sine and Cosine Pre-Calculus 4.2 { Trig Func: The Unit Circle Mr. Niedert 3 / 27 4.2 { Trigonometric Functions: The Unit Circle 1 The Unit Circle 2 Trigonometric Functions 3 Domain and Period of Sine and Cosine 4 Evaluating Trigonometric Functions with a Calculator Pre-Calculus 4.2 { Trig Func: The Unit Circle Mr.
    [Show full text]
  • Coverrailway Curves Book.Cdr
    RAILWAY CURVES March 2010 (Corrected & Reprinted : November 2018) INDIAN RAILWAYS INSTITUTE OF CIVIL ENGINEERING PUNE - 411 001 i ii Foreword to the corrected and updated version The book on Railway Curves was originally published in March 2010 by Shri V B Sood, the then professor, IRICEN and reprinted in September 2013. The book has been again now corrected and updated as per latest correction slips on various provisions of IRPWM and IRTMM by Shri V B Sood, Chief General Manager (Civil) IRSDC, Delhi, Shri R K Bajpai, Sr Professor, Track-2, and Shri Anil Choudhary, Sr Professor, Track, IRICEN. I hope that the book will be found useful by the field engineers involved in laying and maintenance of curves. Pune Ajay Goyal November 2018 Director IRICEN, Pune iii PREFACE In an attempt to reach out to all the railway engineers including supervisors, IRICEN has been endeavouring to bring out technical books and monograms. This book “Railway Curves” is an attempt in that direction. The earlier two books on this subject, viz. “Speed on Curves” and “Improving Running on Curves” were very well received and several editions of the same have been published. The “Railway Curves” compiles updated material of the above two publications and additional new topics on Setting out of Curves, Computer Program for Realignment of Curves, Curves with Obligatory Points and Turnouts on Curves, with several solved examples to make the book much more useful to the field and design engineer. It is hoped that all the P.way men will find this book a useful source of design, laying out, maintenance, upgradation of the railway curves and tackling various problems of general and specific nature.
    [Show full text]
  • Differential and Integral Calculus
    DIFFERENTIAL AND INTEGRAL CALCULUS WITH APPLICATIONS BY E. W. NICHOLS Superintendent Virginia Military Institute, and Author of Nichols's Analytic Geometry REVISED D. C. HEATH & CO., PUBLISHERS BOSTON NEW YORK CHICAGO w' ^Kt„ Copyright, 1900 and 1918, By D. C. Heath & Co. 1 a8 v m 2B 1918 ©CI.A492720 & PREFACE. This text-book is based upon the methods of " limits " and ''rates/' and is limited in its scope to the requirements in the undergraduate courses of our best universities, colleges, and technical schools. In its preparation the author has embodied the results of twenty years' experience in the class-room, ten of which have been devoted to applied mathematics and ten to pure mathematics. It has been his aim to prepare a teachable work for begimiers, removing as far as the nature of the subject would admit all obscurities and mysteries, and endeavoring by the introduction of a great variety of practical exercises to stimulate the student's interest and appetite. Among the more marked peculiarities of the work the follow- ing may be enumerated : — i. A large amount of explanation. 2. Clear and simple demonstiations of principles. 3. Geometric, mechanical, and engineering applications. 4. Historical notes at the heads of chapters giving a brief account of the discovery and development of the subject of which it treats. 5. Footnotes calling attention to topics of special historic interest. iii iv Preface 6. A chapter on Differential Equations for students in mathematical physics and for the benefit of those desiring an elementary knowledge of this interesting extension of the calculus.
    [Show full text]
  • The Unit Circle 4.2 TRIGONOMETRIC FUNCTIONS
    292 Chapter 4 Trigonometry 4.2 TRIGONOMETRIC FUNCTIONS : T HE UNIT CIRCLE What you should learn The Unit Circle • Identify a unit circle and describe its relationship to real numbers. The two historical perspectives of trigonometry incorporate different methods for • Evaluate trigonometric functions introducing the trigonometric functions. Our first introduction to these functions is using the unit circle. based on the unit circle. • Use the domain and period to Consider the unit circle given by evaluate sine and cosine functions. x2 ϩ y 2 ϭ 1 Unit circle • Use a calculator to evaluate trigonometric functions. as shown in Figure 4.20. Why you should learn it y Trigonometric functions are used to (0, 1) model the movement of an oscillating weight. For instance, in Exercise 60 on page 298, the displacement from equilibrium of an oscillating weight x suspended by a spring is modeled as (− 1, 0) (1, 0) a function of time. (0,− 1) FIGURE 4.20 Imagine that the real number line is wrapped around this circle, with positive numbers corresponding to a counterclockwise wrapping and negative numbers corresponding to a clockwise wrapping, as shown in Figure 4.21. y y t > 0 (x , y ) t t < 0 t θ (1, 0) Richard Megna/Fundamental Photographs x x (1, 0) θ t (x , y ) t FIGURE 4.21 As the real number line is wrapped around the unit circle, each real number t corresponds to a point ͑x, y͒ on the circle. For example, the real number 0 corresponds to the point ͑1, 0 ͒. Moreover, because the unit circle has a circumference of 2␲, the real number 2␲ also corresponds to the point ͑1, 0 ͒.
    [Show full text]
  • 4.2 Trigonometric Functions: the Unit Circle
    4.2 Trigonometric Functions: The Unit Circle The two historical perspectives of trigonometry incorporate different The Unit circle: xy221 2 2 3 1 1 3 Example: Verify the points , , , , , ,(1,0) are on the unit circle. 2 2 2 2 2 2 Imaging that the real number line is wrapped around this circle, with positive numbers corresponding to a counterclockwise wrapping and negative numbers corresponding to a clockwise wrapping, as shown in the following. As the real number line is wrapped around the unit circle, each real number t corresponds to a point (,)xy on the circle. For example, the real number corresponding to (0,1) . 2 Remark: In general, each real number t also corresponds to a central angle (in standard position) whose radian measure is t . With this interpretation of t , the arc length formula sr (with r 1 ) indicates that the real number t is the (directional) length of the arc intercepted by the angle , given in radians. In the following graph, the unit circle has been divided into eight equal arcs, corresponding to t -values 3 5 3 7 of 0, , , , , , , ,2 4 2 4 4 2 4 Similarly, in the following graph, the unit circle has been divided into 12 equal arcs, corresponding to t 2 5 7 4 3 5 11 values of 0,,,, , ,, , , , , ,2 6 3 2 3 6 6 3 2 3 6 The Trigonometric Functions. From the preceding discussion, it follows that the coordinates x and y are two functions of the real variable t . You can use these coordinates to define the six trigonometric functions of t .
    [Show full text]
  • 4.1 Unit Circle Cosine & Sine (Slides 4-To-1).Pdf
    The Unit Circle Many important elementary functions involve computations on the unit circle. These \circular functions" are called by a different name, \trigonometric functions." Elementary Functions But the best way to view them is as functions on the circle. Part 4, Trigonometry Lecture 4.1a, The Unit Circle Dr. Ken W. Smith Sam Houston State University 2013 Smith (SHSU) Elementary Functions 2013 1 / 54 Smith (SHSU) Elementary Functions 2013 2 / 54 The Unit Circle The Unit Circle The unit circle is the circle centered at the origin (0; 0) with radius 1. The radius of the circle is one, so P (x; y) is a vertex of a right triangle Draw a ray from the center of the circle out to a point P (x; y) on the with sides x and y and hypotenuse 1. circle to create a central angle θ (drawn in blue, below.) By the Pythagorean theorem, P (x; y) solves the equation x2 + y2 = 1 (1) Smith (SHSU) Elementary Functions 2013 3 / 54 Smith (SHSU) Elementary Functions 2013 4 / 54 Central Angles and Arcs Central Angles and Arcs An arc of the circle corresponds to a central angle created by drawing line segments from the endpoints of the arc to the center. The Babylonians (4000 years ago!) divided the circle into 360 pieces, called degrees. This choice is a very human one; it does not have a natural mathematical reason. (It is not \intrinsic" to the circle.) The most natural way to measure arcs on a circle is by the intrinsic unit of measurement which comes with the circle, that is, the length of the radius.
    [Show full text]
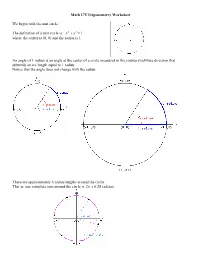
  • Math 175 Trigonometry Worksheet We Begin with the Unit Circle. The
    Math 175 Trigonometry Worksheet We begin with the unit circle. The definition of a unit circle is: x 2 + y 2 =1 where the center is (0, 0) and the radius is 1. An angle of 1 radian is an angle at the center of a circle measured in the counterclockwise direction that subtends an arc length equal to 1 radius. Notice that the angle does not change with the radius. There are approximately 6 radius lengths around the circle. That is, one complete turn around the circle is 2π ≈ 6.28 radians. Define the Sine and Cosine functions: Choose P(x,y) a point on the unit circle where the terminal side of θ intersects with the circle. Then cosθ = x and sinθ = y . We see that the Pythagorean Identity follows directly from these definitions: x 2 + y 2 =1 (cosθ)2 + (sinθ)2 =1 we know it as : sin2 θ + cos2 θ =1 Example 1. Example 2. Determine: Determine: sin(90°) and cos(90°) sin(3π) and cos(3π) π Recall that90° corresponds to radians. (How many degrees do 3π radians correspond to?) 2 We can read the answers from the graphs: ⎛ π ⎞ sin(90°) = sin⎜ ⎟ = y coordinate of P =1 sin(3π) = sin(540°) = y coordinate of P = 0 ⎝ 2 ⎠ ⎛ π ⎞ cos(90°) = cos⎜ ⎟ = x coordinate of P = 0 cos(3π) = cos(540°) = x coordinate of P = −1 ⎝ 2 ⎠ Problems 1 and 2: 1. Locate the following angles on a unit circle and find their sine and cosine. 5π 5π a. − b. c. 360° d. −π 2 2 2.
    [Show full text]
  • Mathematics Tables
    MATHEMATICS TABLES Department of Applied Mathematics Naval Postgraduate School TABLE OF CONTENTS Derivatives and Differentials.............................................. 1 Integrals of Elementary Forms............................................ 2 Integrals Involving au + b ................................................ 3 Integrals Involving u2 a2 ............................................... 4 Integrals Involving √u±2 a2, a> 0 ....................................... 4 Integrals Involving √a2 ± u2, a> 0 ....................................... 5 Integrals Involving Trigonometric− Functions .............................. 6 Integrals Involving Exponential Functions ................................ 7 Miscellaneous Integrals ................................................... 7 Wallis’ Formulas ................................................... ...... 8 Gamma Function ................................................... ..... 8 Laplace Transforms ................................................... 9 Probability and Statistics ............................................... 11 Discrete Probability Functions .......................................... 12 Standard Normal CDF and Table ....................................... 12 Continuous Probability Functions ....................................... 13 Fourier Series ................................................... ........ 13 Separation of Variables .................................................. 15 Bessel Functions ................................................... ..... 16 Legendre
    [Show full text]