DOCSLIB.ORG

Direct Determination of Air Density in a Balance Through Artifacts

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Direct Determination of Air Density in a Balance Through Artifacts JOURNAL OF RESEARCH of the National Bureau of Standards Vol. 83, No.5, Septem ber- October 197B ::> I Dired Detennination of Air Density in a Balance Through Artifads Charaderized in an Evacuated Weighing Chamber. W. F. Koch Center for AnalytiCXJI Oremistry, National Bureau of Standards, Washington, DC 20234 R. S. Davis and V. E. Bower Centerfor Absolute Physirol Quantities, National Bureau of Standards, Washington, DC 20234 June 29, 1978 This paper describes a s imple device wh ich permit s mass comparisons in air without appea l to the correction for ai r buoyancy. The device consists of a ca nister which is evacuated and weighed on a laboratory balance with a mass inside. A second we ighing of another mass in the evacuated cani ster provides th e des ired ma ss com parison. The method was used to deter'm ine the mass difference between two sta inl ess steel weights of widel y differing densi ties. With knowledge of this mass difference and of the volume difference one may, by a simple air weighing of the two objects, determine directl y the densit y of the ai r in the balance case. Densiti es of air d etermin ed by this method were compared with those calc ul ate d from the barometric pressure, the temperature, and the relati ve humidity of the laboratory a ir. The experime nt a l and calculated va lues agree th roughout to within 1.0 fL g cm- 3 (w here the norm al air densit y is about 1.2 mg cm- 3). The calculated and ex perimental values of day-to-day fluc tuations in air densit y agree to wi thin 0.5 p..g cm- 3 . Key wo rd s: Buoyancy of a ir; dens it y; mass compari sons in vacuo; precise we ighing; vacuum; vacuulll weighing. 1. Introduction (NBS) is beli eved to be no greater than 0.3 ppm with respect to the NBS maintained units. To keep to 1-2 ppm the In recent years, th e authors have parti c ipated in two uncertainty of the measure me nt of the Faraday constant, the separate electroc hemi cal studies of the Faraday constant. mass measurements, with all th eir correcti ons, must have an Koch and Diehl made a determinati on of the Faraday by the uncertainty of no greater than about 0.9 ppm, irrespective of coul ometric titrati on of a base, 4-aminopyridine [I];l Bower the materi als used. Of the various corrections to be applied to mass determi­ and Davis have made a series of determinations by the nation, such as those for the sensitivity of the balance, the anodic dissolution of high-purity silver into perchloric acid calibration of the standa rd weights, etc., the correction for solution [2]. Both of these measurements were designed to the air buoyancy appears as the least amenable to d irect provide values of the Faraday constant wi th uncertainties of ,L, determination. For the buoyancy co rrecti on, one almost about one ppm. A constant of such accuracy might make a always relies on a calcula ti on of air de nsity by so me contribution toward the resolution of the discrepancy between algorithm whose entries are such laboratory observables as the values for the Faraday obtained directly (electroc hemi­ the barometric pressure, the te mperature, the relati ve humid­ cally) and indirectl y (by calculation from accurately known it y and , sometimes, the carbon dioxide conte nt of the air. phys ical constants). For details on this last point th e reader The general question of the limits of validity of the various is referred to Taylor et al. [3], and Cohen and Taylor l4]. closely related air density algorithms advanced in the scien­ The accuracy of an electroc hemical measuremen t can be tific literature and the question of the direct precise deter­ no greater than that of the associated mass measurements. mination of air density in a balance chamber are matters of The uncert ainty in th e definiti on and transfe r of the electrical ) considerable moment at present to the metrological commu­ . units into the Faraday laboratory in the Electri cal Measure­ nity. The urgency of these questions, among others, led the ments and Standard s Division, Na ti onal Bureau of Standards Bureau Intern ational des Poids et Mesures to hold a meeting I :> on precision mass determinations in November 1976 at I Figures in brackets indicate lit era ture references allhe end of this paper. Sevres, France [5]. 407 Our study was undertaken with the aim of making direct, to d",=;", the d,n,;ty of the a;' ;n a b,l,." "". If m ~ accurate measurement of the air density in order to confirm the difference in air weight (divided by g) between M Hand the air density algorithm which we used in computing the M s, and if LlV = V H - Vs, buoyancy corrections to the mass determinations required for " the Faraday experiments. m = (Ms - pVs) - (MH - pVH), or (1) ,( p = (LlM + m)/LlV. 2. The Problem and the Method The evaluation of the buoyancy correction to weighings of The values of p so obtained may be compared to those ;:; 4-aminopyridine, aqueous solutions and other low-density calculated from the atmospheric observables. materials offers some difficulties if one uses high-density The vacuum chamber is a stainless steel tube (fig. 1) with (platinum or stainless steel) standards. The density of 4- one end capped. To the other end is attached a stainless aminopyridine is about 1.27 g cm-3 . The weight standards steel flange with a groove in which is set an O-ring whose are made of stainless steel, density about 8 g cm- 3 . For an profile extends slightly above the groove. A separate flat uncertainty of only 1 ppm in the mass of 4-aminopyridine or stainless-steel cover with a stainless-steel vacuum valve aqueous solutions, the density of air, about 0.0012 g cm - 3 at welded to it reposes on the O-ring. A circular land on the room temperature, must be known with an uncertainty no underside keeps the cover centered on the cylindrical cham­ greater than 0.08 percent. ber. To the vacuum valve is welded a smooth stainless steel We have made a direct physical determination of the air tube which serves to attach the whole chamber to a port on a density in a balance chamber and have compared the results pumping station. Removal of excess material from the valve with the version of the algorithm which is given below. The enabled us to keep the mass of the whole assembly, with a ~ experimental method, based on Archimedes' principle, has 17-g weight inside, within the 100-g capacity of our balance. been used successfully before, notably by Baxter [6] who The principal dimensions of the apparatus are approxi­ used a globe to determine his buoyancy corrections, and by mately as follows: length, bottom to flange, 85 mm; inside Jaquerod and Borel l7], who weighed a float in various diameter of chamber, 27 mm; outside diameter of chamber, samples of air under standard conditions in order to obtain 29 mm; outside diameter of fl ange and lid, 33 mm; overall the variation in density. To this end we have employed height 127 mm. stainless steel artifacts to permit direct measurement of Two weights (fig. 1) were constructed of stainless steel, density of air in a balance . We have been anticipated in the one hollow, the other solid. The hollow weight was con­ use of this principle in recent years by Bowman et al. [8] and structed by capping stainless steel tubing, 0.25 mm thick by Bruhlmans and Eschbach [9]. and 25 mm in diameter with stainless steel sheet 1 mm thick. We have fU11hermore employed a method of determining the mass of these objects by comparisons in vacuo. Rather than using the expensive, but perhaps more accurate, method of placing a balance in an evacuable enclosure, we have constructed an evacuable enclosure which may be weighed on a chemist's analytical balance. Let M Hand M s be the nearly equal masses of a hollow, low density weight and a solid, high density weight, respec­ tively. Let the respective exterior volumes be V H and Vs . Let I M Hand M s be weighed, successively, within an evacuate d enclosure of mass ME and exterior volume V E' Calling the air 1 density p, we have the force equation: where 11M represents the small difference indicated on the optical scale of the balance, calibrated with platinum weights, and g represents the local acceleration of gravity. Providing V E and p are constant throughout the procedure, the mass difference, 11M = M H - M s has been obtained without appeal to an air buoyancy calculation. FIGURE 1. Vacuum weighing device consisting of a stainless steel canister Once thus characterized, the two masses M H and M s, if and cover with vacuum valve . The low-density and high-densit y weights for detennining density of air in a balance their mean densities are sufficiently different, may be used chamber appear at right. 408 The joinings were electron-beam weld ed and machined standard we ights of stai nl ess steel in the balance. All smoo th, and the object was polished to a specul ar finish. The weighings are by double substitution with platinum sensiti v­ result was a weight in the form of a right circular cylinder 50 ity weights.
Load more

Recommended publications
  • Air Pressure
    Name ____________________________________ Date __________ Class ___________________ SECTION 15-3 SECTION SUMMARY Air Pressure Guide for ir consists of atoms and molecules that have mass. Therefore, air has Reading A mass. Because air has mass, it also has other properties, includ- ing density and pressure. The amount of mass per unit volume of a N What are some of substance is called the density of the substance. The force per unit area the properties of air? is called pressure. Air pressure is the result of the weight of a column of N What instruments air pushing down on an area. The molecules in air push in all directions. are used to mea- This is why air pressure doesn’t crush objects. sure air pressure? Falling air pressure usually indicates that a storm is approaching. Rising N How does increas- air pressure usually means that the weather is clearing. A ing altitude affect barometer is an instrument that measures changes in air pressure. There air pressure and are two kinds of barometers: mercury barometers and aneroid density? barometers. A mercury barometer consists of a glass tube open at the bottom end and partially filled with mercury. The open end of the tube rests in a dish of mercury, and the space above the mercury in the tube contains no air. The air pressure pushing down on the surface of the mer- cury in the dish is equal to the weight of the column of mercury in the tube. At sea level, the mercury column is about 76 centimeters high, on average. An aneroid barometer has an airtight metal chamber that is sen- sitive to changes in air pressure.
    [Show full text]
  • Effect of Tropospheric Air Density and Dew Point Temperature on Radio (Electromagnetic) Waves and Air Radio Wave Refractivity
    International Journal of Scientific & Engineering Research, Volume 7, Issue 6, June-2016 356 ISSN 2229-5518 Effect of Tropospheric Air density and dew point temperature on Radio (Electromagnetic) waves and Air radio wave refractivity <Joseph Amajama> University of Calabar, Department of Physics, Electronics and Computer Technology Unit Etta-agbor, Calabar, Nigeria [email protected] Abstract: Signal strengths measurements were obtained half hourly for some hours and simultaneously, the atmospheric components: atmospheric temperature, atmospheric pressure, relative humidity and wind direction and speed were registered to erect the effects of air density and dew point temperature on radio signals (electromagnetic waves) as they travel through the atmosphere and air radio wave refractivity. The signal strength from Cross River State Broadcasting Co-operation Television (CRBC-TV), (4057'54.7''N, 8019'43.7''E) transmitted at 35mdB and 519.25 MHz (UHF) were measured using a Cable TV analyzer in a residence along Ettaabgor, Calabar, Nigeria (4057'31.7''N, 8020'49.7''E) using the digital Community – Access (Cable) Television (CATV) analyzer with 24 channels, spectrum 46 – 870 MHz, connected to a domestic receiver antenna of height 4.23 m. Results show that: on the condition that the wind speed and direction are the same or (0 mph NA), the radio signal strength is near negligibly directly proportional to the air density, mathematically Ss / ∂a1.3029 = K, where Ss is Signal Strength in dB, ∂a is Density of air Kg/m3 and K is constant; radio
    [Show full text]
  • Air Infiltration Glossary (English Edition)
    AIRGLOSS: Air Infiltration Glossary (English Edition) Carolyn Allen ~)Copyrlght Oscar Faber Partnership 1981. All property rights, Including copyright ere vested In the Operating Agent (The Oscar Faber Partnership) on behalf of the International Energy Agency. In particular, no part of this publication may be reproduced, stored in a retrieval system or transmitted in any form or by any means, electronic, mechanical, photocopying, recording or otherwise, without the prior written permluion of the operat- ing agent. Contents (i) Preface (iii) Introduction (v) Umr's Guide (v) Glossary Appendix 1 - References 87 Appendix 2 - Tracer Gases 93 Appendix 3 - Abbreviations 99 Appendix 4 - Units 103 (i) (il) Preface International Energy Agency In order to strengthen cooperation In the vital area of energy policy, an Agreement on an International Energy Program was formulated among a number of industrialised countries In November 1974. The International Energy Agency (lEA) was established as an autonomous body within the Organisation for Economic Cooperation and Development (OECD) to administer that agreement. Twenty-one countries are currently members of the lEA, with the Commission of the European Communities participating under a special arrangement. As one element of the International Energy Program, the Participants undertake cooperative activities in energy research, development, and demonstration. A number of new and improved energy technologies which have the potential of making significant contributions to our energy needs were identified for collaborative efforts. The lEA Committee on Energy Research and Development (CRD), assisted by a small Secretariat staff, coordinates the energy research, development, and demonstration programme. Energy Conservation in Buildings and Community Systems The International Energy Agency sponsors research and development in a number of areas related to energy.
    [Show full text]
  • Calculation Exercises with Answers and Solutions
    Atmospheric Chemistry and Physics Calculation Exercises Contents Exercise A, chapter 1 - 3 in Jacob …………………………………………………… 2 Exercise B, chapter 4, 6 in Jacob …………………………………………………… 6 Exercise C, chapter 7, 8 in Jacob, OH on aerosols and booklet by Heintzenberg … 11 Exercise D, chapter 9 in Jacob………………………………………………………. 16 Exercise E, chapter 10 in Jacob……………………………………………………… 20 Exercise F, chapter 11 - 13 in Jacob………………………………………………… 24 Answers and solutions …………………………………………………………………. 29 Note that approximately 40% of the written exam deals with calculations. The remainder is about understanding of the theory. Exercises marked with an asterisk (*) are for the most interested students. These exercises are more comprehensive and/or difficult than questions appearing in the written exam. 1 Atmospheric Chemistry and Physics – Exercise A, chap. 1 – 3 Recommended activity before exercise: Try to solve 1:1 – 1:5, 2:1 – 2:2 and 3:1 – 3:2. Summary: Concentration Example Advantage Number density No. molecules/m3, Useful for calculations of reaction kmol/m3 rates in the gas phase Partial pressure Useful measure on the amount of a substance that easily can be converted to mixing ratio Mixing ratio ppmv can mean e.g. Concentration relative to the mole/mole or partial concentration of air molecules. Very pressure/total pressure useful because air is compressible. Ideal gas law: PV = nRT Molar mass: M = m/n Density: ρ = m/V = PM/RT; (from the two equations above) Mixing ratio (vol): Cx = nx/na = Px/Pa ≠ mx/ma Number density: Cvol = nNav/V 26 -1 Avogadro’s
    [Show full text]
  • CE-087 Calculation of Gas Density and Viscosity
    CE‐087 Calculation of Gas Density and Viscosity Instructor: Harlan Bengtson, PhD, P.E. Course ID: CE‐087 PDH Hours: 2 PDH PDH Star | T / F: (833) PDH‐STAR (734‐7827) | E: [email protected] Calculation of Gas Density and Viscosity Harlan H. Bengtson, PhD, P.E. COURSE CONTENT 1. Introduction The density and/or viscosity of a gas is often needed for some other calculation, such as pipe flow or heat exchanger calculations. This course contains discussion of, and example calculation of, the density and viscosity of a specified gas at a given temperature and pressure. If the gas temperature is high relative to its critical temperature and the gas pressure is low relative to its critical pressure, then it can be treated as an ideal gas and its density can be calculated at a specified temperature and pressure using the ideal gas law. If the density of a gas is needed at a temperature and pressure at which it cannot be treated as an ideal gas law, however, then the compressibility factor of the gas must be calculated and used in calculating its density. In this course, the Redlich Kwong equation will be used for calculation of the compressibility factor of a gas. The Sutherland formula can be used to calculate the viscosity of a gas at a specified temperature and pressure if the Sutherland constants are available for the gas. It will be discussed and used in example calculations. Another method for calculating the viscosity of air at a specified temperature and pressure will also be presented and discussed.
    [Show full text]
  • Use Nitrogen Safely
    Safety Use Nitrogen Safely Paul Yanisko Understanding the potential hazards and Dennis Croll Air Products taking the proper precautions will allow you to reap such benefits as improved product quality and enhanced process safety. itrogen is valued both as a gas for its inert prop- Nitrogen does not support combustion, and at standard erties and as a liquid for cooling and freezing. conditions is a colorless, odorless, tasteless, nonirritating, NBecause of its unique properties, it is used in and inert gas. But, while seemingly harmless, there are haz- a wide range of applications and industries to improve ards associated with the use of nitrogen that require aware- yields, optimize performance, protect product quality, and ness, caution, and proper handling procedures. This article make operations safer (1). discusses those hazards and outlines the precautions that Nitrogen makes up 78% of the atmosphere, with the bal- must be taken to achieve the benefits of using nitrogen in the ance being primarily oxygen (roughly 21%). Most nitrogen safest possible manner. is produced by fractional distillation of liquid air in large plants called air separation units (ASUs). Pressure-swing Nitrogen applications adsorption (PSA) and membrane technologies are also used Many operations in chemical plants, petroleum refin- to produce nitrogen. Nitrogen can be liquefied at very low eries, and other industrial facilities use nitrogen gas to temperatures, and large volumes of liquid nitrogen can be purge equipment, tanks, and pipelines of vapors and gases. effectively transported and stored. Nitrogen gas is also used to maintain an inert and protective atmosphere in tanks storing flammable liquids or air-sensi- tive materials.
    [Show full text]
  • Hazard Analysis CONSEQUENCE ANALYSIS for CHEVRON HYDROGEN PLANT
    Appendix C Hazard Analysis CONSEQUENCE ANALYSIS FOR CHEVRON HYDROGEN PLANT Prepared For Environmental Audit, Inc. 1000-A Ortega Way Placentia, California 92670-7125 Prepared By Quest Consultants Inc.® 908 26th Avenue N.W. Norman, Oklahoma 73069 Telephone: 405-329-7475 Fax: 405-329-7734 03-04-6477 April 21, 2003 QUEST CONSEQUENCE ANALYSIS FOR CHEVRON HYDROGEN PLANT Introduction Quest Consultants Inc. has performed a series of release, vapor dispersion, and fire radiation calculations in an effort to quantify the consequences following a release from various process lines on the premises of Chevron’s proposed Hydrogen Plant in the El Segundo Refinery. The releases were designed to simulate what would happen if one of several lines containing either anhydous ammonia (AnNH3), aqueous ammonia (AqNH3), natural/fuel gas, hydrogen (H2), or pentanes was to fully fail and the material contained therein was released to the environment. Site-Specific Information Several of the parameters defined in the analysis are: Toxic Material Pipelines Proposed AnNH 3 Proposed AqNH Parameters Current AnNH Feed to 3 3 to New Hydrogen Plant Hydrogen Plant Pipeline diameter 2-inch 2-inch 2-inch Aqueous ammonia Material composition Anhydrous ammonia Anhydrous ammonia (30% by weight in water) Temperature 87°F 87°F 87°F Pressure 170 psig 170 psig 180 psig Average flow rate 13 gpm 13 gpm 216 gpd Approximate length of pipeline 5,000 ft 1,100 ft 750 ft Fuel Gas and Pentanes Pipelines Proposed Proposed Proposed Parameters Natural Gas Line Fuel Gas Line Pentanes Line Pipeline
    [Show full text]
  • Revised Formula for the Density of Moist Air (CIPM-2007)
    IOP PUBLISHING METROLOGIA Metrologia 45 (2008) 149–155 doi:10.1088/0026-1394/45/2/004 Revised formula for the density of moist air (CIPM-2007) A Picard1,RSDavis1,MGlaser¨ 2 and K Fujii3 1 Bureau International des Poids et Mesures, Pavillon de Breteuil, F-92310 Sevres` Cedex, France 2 Physikalisch-Technische Bundesanstalt, Bundesallee 100, D-38116 Braunschweig, Germany 3 National Metrology Institute of Japan, National Institute of Advanced Industrial Science and Technology (NMIJ/AIST), Central 3, 1-1, Umezono 1-chome, Tsukuba, Ibaraki 305-8563, Japan Received 8 January 2008 Published 18 February 2008 Online at stacks.iop.org/Met/45/149 Abstract Measurements of air density determined gravimetrically and by using the CIPM-81/91 formula, an equation of state, have a relative deviation of 6.4 × 10−5. This difference is consistent with a new determination of the mole fraction of argon xAr carried out in 2002 by the Korea Research Institute of Standards and Science (KRISS) and with recently published results from the LNE. The CIPM equation is based on the molar mass of dry air, which is dependent on the contents of the atmospheric gases, including the concentration of argon. We accept the new argon value as definitive and amend the CIPM-81/91 formula accordingly. The KRISS results also provide a test of certain assumptions concerning the mole fractions of oxygen and carbon dioxide in air. An updated value of the molar gas constant R is available and has been incorporated in the CIPM-2007 equation. In making these changes, we have also calculated the uncertainty of the CIPM-2007 equation itself in conformance with the Guide to the Expression of Uncertainty in Measurement, which was not the case for previous versions of this equation.
    [Show full text]
  • Buoyancy Correction and Air Density Measurement
    Buoyancy Correction Note 5/2/03 10:07 am Page 2 Good Practice Guidance Note Buoyancy Correction and Air Density Measurement Introduction Determination of Contents This Guidance Note gives Air Density recommendations of good mass Introduction 1 I The usual method of determining air measurement practice in calculating density is to measure temperature, air density and buoyancy corrections Need for the Determination 1 pressure and humidity and calculate but should not be considered a of Air Density air density using the equation comprehensive guide. recommended by the Comité What is the Typical Density 1 International des Poids et Mesures of the Air? Need for the (CIPM) (derived by Giacomo [2] and modified by Davis [3]). The equation Determination of Air 1 Determination of is not a perfect model of air density Density and introduces an uncertainty of Air Density approximately 1 part in 104. Air Density Artefacts 2 I I Air is dense Typical routine measurement capabilities for the air density Variation in Buoyancy 2 A cubic metre of air weighs parameters are indicated as follows Effect with Varying approximately 1.2 kilograms with the best measurement Air Density A 1 kilogram stainless steel capabilities in brackets: weight displaces 150 mg of air When Should I make a 3 Temperature to 0.1 °C (0.01 °C) I The density of air can vary between Buoyancy Correction? about 1.1 kg m-3 and 1.3 kg m-3, Pressure to 0.5 mbar (0.05 mbar) How do I make a 3 which is equivalent to a change of Relative Humidity to 5% (0.25 °C 25 mg in the weight of a stainless dew point) Buoyancy Correction? steel kilogram of volume 125 cm3.
    [Show full text]
  • Composition of the Atmosphere Density of Air Density
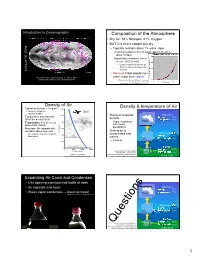
    Introduction to Oceanography Composition oF the Atmosphere • Dry Air: 78% Nitrogen, 21% Oxygen • BUT it is never completely dry – Typically contains about 1% water vapor Chemical residence time oF water vapor in the air is Wind about 10 days 15: 15: (liquid water residence time in ocean: 3x103 years!) – Liquid evaporates into the air, then is removed as dew, rain, Lecture Lecture or snow – Warm air holds much more Atmospheric water vapor map, Sept. 13 – Nov. 2, 2017. water vapor than cold air Data from http://www.ssec.wisc.edu/data/comp/wv/ Figure by Greg Benson, Wikimedia Commons Creative Commons A S-A 3.0, http://en.wikipedia.org/wiki/File:Dewpoint.jpg Density oF Air 3 Density & temperature oF Air • Typical air density ~ 1 mg/cm 12000 – About 1/1000th the Passenger jet 10-13km density of water 10000 • Rising air expands 2000 meters • Temperature and pressure 15ºC Everest 8848m & cools afFect the density of air 15ºC • Temperature: Hot air is less 8000 – Vapor condenses dense than cold air into clouds, precipitation • Pressure: Air expands with 6000 elevation above sea level • Sinking air is Elevation (m) Elevation Mt. Whitney 4421m compressed and 1000 meters – Air is much easier to compress 4000 than water warms 24ºC 15ºC – Clear air 2000 Empire State Bldg. 450m 0 0 40000 80000 120000 34ºC Pressure (N/m2) Figure adapted from Nat’l Weather Service/NOAA, Public Domain, 15ºC Figure by E. Schauble, http://oceanservice.noaa.gov/education/yos/r using NOAA Standard Atmosphere data. esource/JetStream/synoptic/clouds.htm (1.4% H2O) Expanding Air Cools and Condenses • Like opening a pressurized bottle of soda • Air expands and cools 2000 meters 15ºC • Water vapor condenses -- cloud Formation 15ºC MMovies by J.
    [Show full text]
  • Chapter 4: Principles of Flight
    Chapter 4 Principles of Flight Introduction This chapter examines the fundamental physical laws governing the forces acting on an aircraft in flight, and what effect these natural laws and forces have on the performance characteristics of aircraft. To control an aircraft, be it an airplane, helicopter, glider, or balloon, the pilot must understand the principles involved and learn to use or counteract these natural forces. Structure of the Atmosphere The atmosphere is an envelope of air that surrounds the Earth and rests upon its surface. It is as much a part of the Earth as the seas or the land, but air differs from land and water as it is a mixture of gases. It has mass, weight, and indefinite shape. The atmosphere is composed of 78 percent nitrogen, 21 percent oxygen, and 1 percent other gases, such as argon or helium. Some of these elements are heavier than others. The heavier elements, such as oxygen, settle to the surface of the Earth, while the lighter elements are lifted up to the region of higher altitude. Most of the atmosphere’s oxygen is contained below 35,000 feet altitude. 4-1 Air is a Fluid the viscosity of air. However, since air is a fluid and has When most people hear the word “fluid,” they usually think viscosity properties, it resists flow around any object to of liquid. However, gasses, like air, are also fluids. Fluids some extent. take on the shape of their containers. Fluids generally do not resist deformation when even the smallest stress is applied, Friction or they resist it only slightly.
    [Show full text]
  • The Calculation of Air Density in Various Units *
    VOL. 30, No. 9, NOVEMBER, 1949 319 The Calculation of Air Density in Various Units * NELSON R. WILLIAMS U. S. Naval Ordnance Test Station, Inyo kern, California IR density enters into many important Law, the density p can be computed from: problems in meteorology, related sciences, p = (p - 0.37Se)/RdT A and engineering. For example, at the Naval Ordnance Test Station, knowledge of air = C(p - 0.37Se)/T « C(p - Vse)/T, (1) density is necessary for determining the drag co- where p is total pressure of the air, e is partial efficient of a missile and correction curves for the pressure of water vapor, Rd is the gas constant for refraction of light in the atmosphere. The me- dry air = 2.870 X 106 ergs/gm °K, T is the abso- teorologist, in his increasing contact with other lute temperature (°K) of the air, and the constant scientists and industrial engineers, often is called C is a combination of 1 /Rd and the factor neces- upon to calculate air density in units other than sary for conversion to the particular unit desired. those used in meteorology. He is then confronted The value given for Rd agrees very well with the by the necessity of laboriously working out con- experiment. The accuracy of humidity measure- version factors to compute the desired density, ments does not justify carrying beyond the third since meteorologists commonly do not use density decimal place the factor by which e is multiplied. directly as a parameter, and therefore the formu- From the definition of the mixing ratio w, the las in the meteorology textbooks usually have to vapor pressure can be expressed by be solved explicitly for the density, and the con- stants evaluated according to the units of meas- pw urement.
    [Show full text]