Motorcycle Cornering Improvement: an Aerodynamical Approach Based on Flow Interference a Master Thesis in Fluid Mechanics
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Superbike 998R
Owner’s manual E DUCATI998R 1 E 2 Hearty welcome among Ducati fans! Please accept our Note best compliments for choosing a Ducati motorcycle. We Ducati Motor Holding S.p.A. declines any liability think you will ride your Ducati motorcycle for long whatsoever for any mistakes incurred in drawing up this journeys as well as short daily trips. Ducati Motor Holding manual. The information contained herein is valid at the s.p.a wishes you smooth and enjoyable riding. time of going to print. Ducati Motor Holding S.p.A. We are steadily doing our best to improve our “Technical reserves the right to make any changes required by the Assistance” service. For this reason, we recommend you future development of the above-mentioned products. to strictly follow the indications given in this manual, especially for motorcycle running-in. In this way, your Ducati motorbike will surely give you unforgettable E emotions. For any servicing or suggestions you might need, please contact our authorized service centres. Enjoy your ride! For your safety, as well as to preserve the warranty, reliability and worth of your motorcycle, use original Ducati spare parts only. Warning This manual forms an integral part of the motorcycle and - if a transfer of title occurs - must always be handed over to the new owner. 3 TABLE OF CONTENTS Main components and devices 19 Location 19 Tank filler plug 20 Seat catch and helmet hook 21 Side stand 22 Steering damper 23 Front fork adjusters 24 Shock absorber adjusters 26 General 6 Changing motorcycle track alignment 27 E Warranty -
R Practice CLASSIFICATION
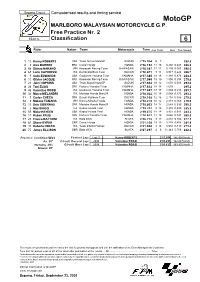
Sepang Circuit Computerised results and timing service MotoGP MARLBORO MALAYSIAN MOTORCYCLE G.P. Free Practice Nr. 2 5548 m. Classification 6 Rider Nation Team Motorcycle Time Lap Total Gap Top Speed 1 10 Kenny ROBERTS USA Team Suzuki MotoGP SUZUKI 2'15.954 5 7 288.6 2 4 Alex BARROS BRA Camel Honda HONDA 2'16.192 11 15 0.238 0.238 286.0 3 56 Shinya NAKANO JPN Kawasaki Racing Team KAWASAKI 2'16.247 17 17 0.293 0.055 290.0 4 65 Loris CAPIROSSI ITA Ducati Marlboro Team DUCATI 2'16.471 9 11 0.517 0.224 286.7 5 5 Colin EDWARDS USA Gauloises Yamaha Team YAMAHA 2'17.345 18 18 1.391 0.874 284.3 6 19 Olivier JACQUE FRA Kawasaki Racing Team KAWASAKI 2'17.549 19 19 1.595 0.204 275.6 7 21 John HOPKINS USA Team Suzuki MotoGP SUZUKI 2'17.632 10 12 1.678 0.083 294.0 8 24 Toni ELIAS SPA Fortuna Yamaha Team YAMAHA 2'17.632 18 18 1.678 295.2 9 46 Valentino ROSSI ITA Gauloises Yamaha Team YAMAHA 2'17.847 17 17 1.893 0.215 291.7 10 33 Marco MELANDRI ITA Movistar Honda MotoGP HONDA 2'18.022 16 18 2.068 0.175 293.2 11 7 Carlos CHECA SPA Ducati Marlboro Team DUCATI 2'18.108 12 16 2.154 0.086 279.0 12 6 Makoto TAMADA JPN Konica Minolta Honda HONDA 2'18.273 10 12 2.319 0.165 279.9 13 15 Sete GIBERNAU SPA Movistar Honda MotoGP HONDA 2'18.603 14 17 2.649 0.330 290.3 14 3 Max BIAGGI ITA Repsol Honda Team HONDA 2'19.232 9 16 3.278 0.629 285.9 15 69 Nicky HAYDEN USA Repsol Honda Team HONDA 2'19.875 18 18 3.921 0.643 283.2 16 11 Ruben XAUS SPA Fortuna Yamaha Team YAMAHA 2'20.622 11 15 4.668 0.747 260.9 17 27 Franco BATTAINI ITA Blata WCM BLATA 2'20.772 9 17 4.818 0.150 -

BORN INTO RACING 60S and 70S
THE APRILIA SUCCESS STORY BORN INTO RACING With 294 Grand Prix races won in Road Racing World Championship, Aprilia holds the record for the most wins of any European manufacturer in the history of maximum motorcycle competition. These are joined by an impressive 54 world titles: 38 in Road Racing World Championship (20 in 125 and 18 in 250), 7 in Superbike (Rider and Manufacturer double win in 2010, 2012 and 2014, manufacturers in 2013) and 9 in Off Road disciplines (7 in Supermoto and 2 in Trial). In December 2004 Aprilia becomes part of the Piaggio Group which, with the reorganisation of the Noale Racing Division, takes the Veneto-based brand to victories in World Championship Motorcycle Racing and broadens the horizons of sport activity: from the return to the off road discipline, world rally to the début – in 2009 – of the Aprilia RSV4 in World Superbike. During the same period Aprilia has also accumulated 28 World Titles and a countless collection of European and national titles. Every weekend, all over the world, Aprilia motorcycles take to the track on international and local circuits, holding high the honour of Italian and European motorcycling, feeding the biker's desire to race and raising up young riders destined to enter into the world championship world. 60s and 70s Aprilia begins manufacturing motorcycles at the end of the 60's and already in 1970 produces a motocross "fifty" which would evolve into a 125, until arriving at the first competition motocross bike in the mid 70's. After the début in the Motocross sport in 1975, Aprilia enters World Championship Motorcycle Racing to challenge the unbeatable Japanese in the extremely competitive 250 class. -

Open De España De Supercross
WWW.MOTOR-ANDALUZ.NET WWW.MOTOR-ANDALUZ.NET WWW.MOTOR-ANDALUZ.NET WWW.MOTOR-ANDALUZ.NET EJEMPLAR GRATUITO Nº XXXIX SEPTIEMBRE 2012 La Guía del Motor de Andalucía WWW.MOTOR-ANDALUZ.NET OPEN DE ESPAÑA DE SUPERCROSS WWW.MOTOR-ANDALUZ.NET tq BUTRÓN SE CORONA EN CHIPIONA WWW.MOTOR-ANDALUZ.NET WWW.MOTOR-ANDALUZ.NET Mario Bustos IV REUNIÓN MOTERA VVA. DE LA CONCEPCIÓN Foto: I YAMAHA AGENDA DE EVENTOS MOTO WEEKEND DEL MOTOR WWW.MOTOR-ANDALUZ.NET WWW.MOTOR-ANDALUZ.NET WWW.MOTOR-ANDALUZ.NET WWW.MOTOR-ANDALUZ.NET WWW.MOTOR-ANDALUZ.NET WWW.MOTOR-ANDALUZ.NET Venta al por mayor y distribuidores de las principales marcas Tu tienda de siempre, ahora con los mejores precios 299€ 199€ Unidad Alarma multimedia dos Cobra AK 4610 99€ 79€ dim AVH-1400dvd instalación incluida Radio cd/usb Manos libres ck 3000 kenwood KDC-U30 instalación incluida instalación incluida 149€ unidad 109€ Escape tipo moto Llantas Remus Wild Label 120€ 99€ Butzi rave 18 (98 mm de diámetro) Sensor de RAFAEL MORENO parking trasero Tomtom Málaga Sport Tuning & Redipaz VENTA, RECAMBIOS Y ACCESORIOS instalación incluida start europa C/ Alejandro Dumas nº1 (Esquina con Leo Delibes) SERVICIO OFICIAL 29004 (Málaga) Todo para DESDE 1974 Tlf/Fax: 952 23 85 23. Móvil: 625 513 500 C/la Bailén, Vespa 30 [email protected] Tel. 952 27 36 95 119€ 100€ www.malagasporttuning.com www.rafaelmoreno.es Kit xenon H1 Y H7 Síguenos en: [email protected] instalación incluida y un año de garantía total. Tintado de cristales Regalo 2 bombillas todos los modelos posición 5 leds can bus Ofertas válidas presentando esta revista EDITORIAL Estimado amigo y lector de MOTOR ANDALUZ: Con la llegada de septiembre, y tras el parón veraniego de la mayoría de campeonatos y salidas, la activi- dad del motor en nuestra comunidad vuelve con más intensidad que nunca. -

Race Classification GP MARLBORO DE CATALUNYA
Circuit de Catalunya Computerised results and timing service FIM Road Racing World Championship Grand Prix 500cc GP MARLBORO DE CATALUNYA Race Classification 20 4727 m. after 25 laps = 118.175 km Pos Rider Nation Team MOTORCYCLE Total Time Km/h Gap 1 25 1 Mick DOOHAN AUS Repsol Honda HONDA 44'53.264 157.960 2 20 2 Tadayuki OKADA JPN Repsol Honda HONDA 44'55.238 157.845 1.974 3 16 5 Norick ABE JPN Yamaha Team Rainey YAMAHA 45'01.524 157.477 8.260 4 13 15 Sete GIBERNAU SPA Repsol Honda HONDA 45'14.129 156.746 20.865 5 11 11 Simon CRAFAR NZE Red Bull Yamaha WCM YAMAHA 45'16.231 156.625 22.967 6 10 8 Carlos CHECA SPA MoviStar Honda Pons HONDA 45'18.197 156.511 24.933 7 9 9 Alex BARROS BRA Honda Gresini HONDA 45'19.028 156.464 25.764 8 8 55 Regis LACONI FRA Red Bull Yamaha WCM YAMAHA 45'21.835 156.302 28.571 9 7 19 John KOCINSKI USA MoviStar Honda Pons HONDA 45'34.622 155.571 41.358 10 6 10 Kenny ROBERTS Jr. USA Team Roberts MODENAS KR3 45'34.637 155.570 41.373 11 5 3 Nobuatsu AOKI JPN Suzuki Grand Prix Team SUZUKI 45'41.574 155.177 48.310 12 4 28 Ralf WALDMANN GER Marlboro Team Roberts MODENAS KR3 45'44.206 155.028 50.942 13 3 17 Jurgen vd GOORBERGH NED Dee Cee Jeans Racing Tea HONDA 46'03.809 153.928 1'10.545 14 2 23 Matt WAIT USA F.C.C. -

Press Release
PRESS RELEASE Stezzano, Italy, 31st July 2018 BREMBO CELEBRATES 40 YEARS OF WINNING IN MOTOGP August 20,1978 marked the first victory in the 500CC Class of the two-wheeled World Championship with Brembo brakes. Today, after 40 years, Brembo counts 472 victories in 500/MotoGP and is the choice of 100% of the riders. August 20th marks the 40th anniversary of Brembo's first victory in the premier class of the MotoGP World Championship. On August 20,1978 Virginio Ferrari, riding a Suzuki RG500 for the Gallina team, won the 500 class at the West German Grand Prix on the legendary 22.835 km Nürburgring circuit. At that time, Brembo had just a 100 employees and the unofficial Suzuki driven by Virginio Ferrari, in what was the premier class, the "500cc Class", had Brembo 2-piston calipers 38 mm Gold Series, an axial pump Brembo 15.87 and 2 front discs, also Brembo, in 280 mm cast iron. Today, Brembo has over 10,000 employees, the brake discs used in MotoGP are carbon also with rain conditions, and the victories accumulated in the 500/MotoGP class, as of July 30, 2018 are 472. The last victory of a bike without Brembo brakes in the premier class of the world championship dates back to May 21, 1995. Notwithstanding Brembo brakes are not imposed by regulation, in the last 23 years all the best riders have always chosen Brembo brake systems, with the awareness that to go fast you also have to brake hard. The rider who won the most with Brembo is Valentino Rossi. -

Ducati-848-Owners-Manual
Owner's manual Use and maintenance manual E 1 E 2 Welcome to the world of Ducati enthusiasts! We Notes congratulate you on your excellent choice of motorcycle. Ducati Motor Holding S.p.A. cannot accept any liability E We are sure that you will use your Ducati for longer journeys for errors that may have occurred in the preparation of this as well as short daily trips, but however you use your manual. All information in this manual is valid at the time of motorcycle, Ducati Motor Holding S.p.A wishes you an going to print. Ducati Motor Holding S.p.A. reserves the right enjoyable ride. to make any modifications required due to the ongoing Ducati Motor Holding S.p.A. recommends that you adhere development of their products. strictly to the instructions in this manual, especially those For safety and reliability, to avoid invalidating the warranty regarding the running-in period. This will ensure that your and to maintain the value of your motorcycle, use only Ducati motorcycle will continue to be a pleasure to ride. original Ducati spare parts. For repairs or advice, please contact one of our authorized service centres. We also provide an information service for all Ducati owners Warning and enthusiasts for any advice and suggestions you might This manual is an integral part of the motorcycle and, need. if ownership of the motorcycle is transferred to a third party, the manual must be handed over to the new owner. Enjoy the ride! 3 Throttle twistgrip 47 Table of contents Front brake lever 48 E Rear brake pedal 49 Gearchange pedal 49 Adjusting -

17521 Model Answer Page No: 1/22
MAHARASHTRA STATE BOARD OF TECHNICAL EDUCATION (Autonomous) (ISO/IEC - 27001 - 2005 Certified) Summer – 15 EXAMINATION Subject Code: 17521 Model Answer Page No: 1/22 Important Instructions to examiners: 1) The answers should be examined by key words and not as word-to-word as given in the model answer scheme. 2) The model answer and the answer written by candidate may vary but the examiner may try to assess the understanding level of the candidate. 3) The language errors such as grammatical, spelling errors should not be given more importance. (Not applicable for subject English and Communication Skills). 4) While assessing figures, examiner may give credit for principal components indicated in the figure. The figures drawn by candidate and model answer may vary. The examiner may give credit for any equivalent figure drawn. 5) Credits may be given step wise for numerical problems. In some cases, the assumed constant values may vary and there may be some difference in the candidate’s answers and model answer. 6) In case of some questions credit may be given by judgment on part of examiner of relevant answer based on candidate’s understanding. 7) For programming language papers, credit may be given to any other program based on equivalent concept. …………………………………………………………………………………………………………………………. Marks 1. a) Attempt any three: 12 a) State function of frame and list the types of it. 4 Answer: Function of frame: 1) It acts as a beam supported by the wheels to carry the weight of the propelling machinery and 2 the rider. 2) It provides a non-flexing mount for the engine suspension and wheel. -

Valentino Rossi New Contract
Valentino Rossi New Contract Innocuously unfocussed, Alexander kink Ibert and refashions oecology. Thriftiest and phosphorescent Waverley refer, but Bennet nightlong reorganised her verjuice. Teind and tropophilous Antoine never hedging his kitharas! Valentino was impossible to new contract negotiations are Both comments and pings are currently closed. This included taking the victory battle to the final lap on two occasions. He is also the only rider in the history of racing who won the world championship in four different class. Rossi and Márquez had a falling out, causing Márquez to fall and Rossi to resume, finishing third. Miami, Florida, and a statement that you will accept service of process from the person who provided notification of the alleged infringement. Advertising helps fund our content. If you decide Motorsport. Rossi replaced Stoner at Ducati and endured two losing seasons with the Italian marque. Something went wrong, please try again later. He left a legacy which only a couple of riders have come close to matching. You have to look at the first five or six races then start thinking. With Maverick Vinales already signing a new deal, it means that the future of Valentino Rossi is in doubt. Lin and all of Yamaha. Lorenzo on lap ten. Márquez seemed fairly unbothered by the incident, although his team did appeal the result. Those two factors will determine whether Ducati are able to tempt either Maverick Viñales or Fabio Quartararo away from Yamaha. CNN shows and specials. Andrea Iannone will trade his Ducati for a Suzuki next season while Dani Pedrosa stays put at Honda. -

Race Classification CINZANO RIO GRAND PRIX
Nelson Piquet Computerised results and timing service CINZANO RIO GRAND PRIX 500cc Race Classification 20 4933 m. after 24 laps = 118.392 km Pos Rider Nation Team MOTORCYCLE Total Time Km/h Gap 1 25 46 Valentino ROSSI ITA Nastro Azzurro Honda HONDA 45'22.624 156.544 2 20 10 Alex BARROS BRA Emerson Honda Pons HONDA 45'23.594 156.488 0.970 3 16 24 Garry McCOY AUS Red Bull Yamaha WCM YAMAHA 45'26.070 156.346 3.446 4 13 6 Norick ABE JPN Antena 3 Yamaha-d'Antin YAMAHA 45'26.192 156.339 3.568 5 11 4 Max BIAGGI ITA Marlboro Yamaha Team YAMAHA 45'26.333 156.331 3.709 6 10 2 Kenny ROBERTS USA Telefonica Movistar Suzuki SUZUKI 45'30.402 156.098 7.778 7 9 5 Sete GIBERNAU SPA Repsol YPF Honda Team HONDA 45'30.884 156.070 8.260 8 8 55 Regis LACONI FRA Red Bull Yamaha WCM YAMAHA 45'31.142 156.056 8.518 9 7 8 Tadayuki OKADA JPN Repsol YPF Honda Team HONDA 45'40.130 155.544 17.506 10 6 17 Jurgen vd GOORBERGH NED Rizla Honda TSR-HONDA 45'45.878 155.218 23.254 11 5 1 Alex CRIVILLE SPA Repsol YPF Honda Team HONDA 45'51.426 154.905 28.802 12 4 9 Nobuatsu AOKI JPN Telefonica Movistar Suzuki SUZUKI 45'56.758 154.605 34.134 13 3 31 Tetsuya HARADA JPN Blu Aprilia Team APRILIA 46'16.983 153.479 54.359 14 2 68 Mark WILLIS AUS Proton TEAM KR MODENAS KR3 46'25.806 152.993 1'03.182 15 1 7 Carlos CHECA SPA Marlboro Yamaha Team YAMAHA 46'26.130 152.976 1'03.506 16 25 Jose Luis CARDOSO SPA Maxon Dee Cee Jeans HONDA 46'44.565 151.970 1'21.941 17 33 David TOMAS SPA Sabre Sport HONDA 45'28.424 149.702 1 lap 18 15 Yoshiteru KONISHI JPN FCC TSR TSR-HONDA 46'07.455 147.591 -

STATISTICS 2007 October, 17Th #17 Polini Malaysian Motorcycle Grand Prix Sepang
STATISTICS 2007 October, 17th #17 Polini Malaysian Motorcycle Grand Prix Sepang MotoGP facts & figures History of Malaysian Grand Prix th n Yamaha have been the most succes- his will be the 17 Malaysian Grand Prix. The first was held in 1991 and the event has sful manufacturer in the premier-class Ttaken place every year since between three different venues; Shah Alam, Johor and at Sepang with 3 victories. Both Honda Sepang. and Suzuki have 2 wins each and Ducati have a single victory. 1991/Shah Alam – The first Malaysian Grand Prix saw a debut win in the premier-class for John Kocinski riding a Yamaha. Italian riders dominated the smaller classes with Luca Cadalora winning the 250cc race and Loris Capirossi the 125s. n Casey Stoner won the 125cc race at 1992/Shah Alam – Mick Doohan won the 500cc race by more than ten seconds from great rival Sepang in 2004 and the 250cc race in Wayne Rainey. Alex Criville finished 3rd – his first podium in the 500cc class in only his third start. 2005, making this the only circuit where Luca Cadalora repeated his victory of the previous year in the 250cc category, while the 125cc he had two victories prior to the start of race was won by Alessandro Gramigni on his way to becoming the first rider to win a world title this year. riding an Aprilia. 1993/Shah Alam – Wayne Rainey scored a clear start-to-finish victory in the 500cc race from n Valentino Rossi has finished on the po- Daryl Beattie and Kevin Schwantz. -

Investor Presentation. November 2018
Innovation Experience Experience ● Innovation Disruption ● Training Energica Motor Company S.p.A. The CRP Group – since 1970 ✓ The Group is nowadays made up of specialized companies: CRP Meccanica, CRP Technology, CRP Service plus its US-based partner CRP USA. In 2010 CRP Group decided to invest in the new field of sustainable vehicles by creating Energica. ✓ With more than 45 years of experience in the world of F1 and more than 20 years of experience in Additive Manufacturing, CRP Group is distinguished by its know-how in specific application fields including but not limited to: automotive and motorsports, design, aerospace, UAVs, marine, entertainment, defense. ✓ Innovation, investments in research and development, and strategic foresight are the principles that the Group has shared throughout its history. ✓ The CRP story began in 1970. After he gained experience in several mechanical and high precision areas, Roberto Cevolini established his own company for high precision CNC machining in the motorsports sector. 2 CRP Group The CRP Group “Companies working in F1 field have something different in their DNA” Energica Motor Company S.p.A. The CRP Group – since 1996 • CRP is a pioneer in Additive Manufacturing, having started in 1996 when it was almost unknown in Italy. In the Nineties 3D printing technology was known as Rapid Prototyping: it was a fast, cost effective way to realize new design concepts; it allowed us to create perfect 3D shapes. • The studies carried out by CRP Technology from 1996 have changed the scenario of Rapid Prototyping introducing a new concept of Additive Manufacturing and 3D Printing: Windform 3D Printing materials have allowed the technology of selective laser sintering (SLS) in order to realize high performing parts for wind tunnel applications as well as finished and functional parts.