The Jumbo-Conforming Spread: a Semiparametric Approach
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Mortgage Finance: Final Report and Recommendations
Mortgage finance: final report and recommendations November 2008 Mortgage finance: final report and recommendations November 2008 © Crown copyright 2008 The text in this document (excluding the Royal Coat of Arms and departmental logos) may be reproduced free of charge in any format or medium providing that it is reproduced accurately and not used in a misleading context. The material must be acknowledged as Crown copyright and the title of the document specified. Where we have identified any third party copyright material you will need to obtain permission from the copyright holders concerned. For any other use of this material please write to Office of Public Sector Information, Information Policy Team, Kew, Richmond, Surrey TW9 4DU or e-mail: [email protected] HM Treasury contacts This document can be found in full on our website at: hm-treasury.gov.uk If you require this information in another language, format or have general enquiries about HM Treasury and its work, contact: Correspondence and Enquiry Unit HM Treasury 1 Horse Guards Road London SW1A 2HQ Tel: 020 7270 4558 Fax: 020 7270 4861 E-mail: [email protected] Printed on at least 75% recycled paper. When you have finished with it please recycle it again. ISBN 978-1-84532-514-5 PU649 Contents Page Foreword 3 Chapter 1 Introduction 11 Chapter 2 Global economic and market developments 17 Chapter 3 UK market developments 25 Chapter 4 The policy context 33 Chapter 5 Industry-led reforms 39 Chapter 6 Government interventions 45 Annex A Consultation list 51 Mortgage finance: final report and recommendations 1 Foreword The Rt Hon Alistair Darling MP Chancellor of the Exchequer Since HM Treasury published my interim report on 29 July, I have continued my dialogue with market commentators and participants to ensure that, in a rapidly deteriorating environment, my conclusions are as relevant as possible. -

AIG Investments Jumbo Underwriting Guidelines
AIG Investments Jumbo Underwriting Guidelines December 20, 2019 These AIG Investments Jumbo Underwriting Guidelines (Exhibit A-2) are dated December 20, 2019. The Underwriting Guidelines may be updated or modified from time to time. AIG Investments believes the information contained in this document relating to state laws and third party requirements to be accurate as of January 1, 2020. However, this information is provided for informational purposes only and may change at any time without notice. AIG Investments is providing this information without any warranties, express or implied. © 2019 AIG Investments. All Rights Reserved. AIG Investments is an affiliate of American International Group, Inc. ("AIG”). AIG Investments is the program administrator for this program and not the purchaser of the loan. Please refer to the AIG Investments Correspondent Seller's Guide for additional information regarding the relationship between the parties. MC-2-A987C-1016 Table of Contents Table of Contents ..................................................................................................................................................................................................................... 1 Jumbo Loan Underwriting Introduction ................................................................................................................................................................................. 5 Chapter One: General ..................................................................................................................................................................................................... -

CITY of BREMERTON, WASHINGTON PLANNING COMMISSION AGENDA ITEM AGENDA TITLE: Workshop to Discuss Nonconformities and Substitute Senate Bill 5451
Commission Meeting Date: March 20, 2012 Agenda Item: V.B.1 CITY OF BREMERTON, WASHINGTON PLANNING COMMISSION AGENDA ITEM AGENDA TITLE: Workshop to discuss Nonconformities and Substitute Senate Bill 5451. DEPARTMENT: Community Development PRESENTED BY: Nicole Floyd, City Planner SUMMARY: This workshop is part of a series of workshops to discuss the Draft Shoreline Master Program (SMP) update. Each workshop focuses on a different set of topics and or sections of the code. The Planning Commission has held two previous workshops focusing on general nonconformities and how they are applicable to the Shoreline Master Program. This workshop will focus on the potential impacts of utilizing the allowed language from Substitute Senate Bill (SSB) 5451in relationship to the nonconforming provisions of the Shoreline Master Program Update. In summary, the Bill was drafted to clarify The Department of Ecology’s review authority over the Statewide SMP update process. Specifically, it is not Ecology’s responsibility to determine what terms are used when referring to existing residential structures. Statewide, this means that there will continue to be substantial variation as to how local jurisdictions address nonconformities within the Shoreline. For Bremerton, it provides the opportunity to change how nonconformities are classified and how they are regulated. This report aims to help provide a better understanding of the underlying issues surrounding the optional language changes to the nonconforming code section. Staff is asking the Planning Commission to provide direction by answering the following questions: 1. Should the City create an alternate name for legal nonconforming residential structures on the shoreline; and 2. Should the City allow for the full replacement of such residential structures an unlimited number of times? Please keep these questions in mind when reading the report and reviewing the attachments, as the report is intended to help provide a wide range of data surrounding these two questions. -

Housing and the Financial Crisis
This PDF is a selection from a published volume from the National Bureau of Economic Research Volume Title: Housing and the Financial Crisis Volume Author/Editor: Edward L. Glaeser and Todd Sinai, editors Volume Publisher: University of Chicago Press Volume ISBN: 978-0-226-03058-6 Volume URL: http://www.nber.org/books/glae11-1 Conference Date: November 17-18, 2011 Publication Date: August 2013 Chapter Title: The Future of the Government-Sponsored Enterprises: The Role for Government in the U.S. Mortgage Market Chapter Author(s): Dwight Jaffee, John M. Quigley Chapter URL: http://www.nber.org/chapters/c12625 Chapter pages in book: (p. 361 - 417) 8 The Future of the Government- Sponsored Enterprises The Role for Government in the US Mortgage Market Dwight Jaffee and John M. Quigley 8.1 Introduction The two large government- sponsored housing enterprises (GSEs),1 the Federal National Mortgage Association (“Fannie Mae”) and the Federal Home Loan Mortgage Corporation (“Freddie Mac”), evolved over three- quarters of a century from a single small government agency, to a large and powerful duopoly, and ultimately to insolvent institutions protected from bankruptcy only by the full faith and credit of the US government. From the beginning of 2008 to the end of 2011, the two GSEs lost capital of $266 billion, requiring draws of $188 billion under the Treasured Preferred Stock Purchase Agreements to remain in operation; see Federal Housing Finance Agency (2011). This downfall of the two GSEs was primarily a question of “when,” not “if,” given that their structure as a public/private Dwight Jaffee is the Willis Booth Professor of Banking, Finance, and Real Estate at the University of California, Berkeley. -
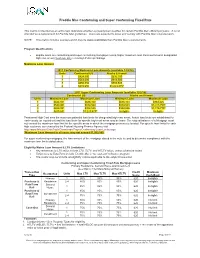
Freddie Mac Conforming and Super Conforming Fixed Rate
Freddie Mac Conforming and Super Conforming Fixed Rate This matrix is intended as an aid to help determine whether a property/loan qualifies for certain Freddie Mac offered programs. It is not intended as a replacement for Freddie Mac guidelines. Users are expected to know and comply with Freddie Mac’s requirements. NOTE: This matrix includes overlays which may be more restrictive than Freddie Mac’s requirements. Program Qualifications x Eligible loans are conforming and super conforming mortgages (using higher maximum loan limits permitted in designated high cost areas) fixed rate only receiving LP Accept findings Maximum Loan Amount 2017 Conforming Maximum Loan Amounts (available 12/2/16) Units Continental US Alaska & Hawaii 1 $424,100 $636,150 2 $543,000 $814,500 3 $656,350 $984,525 4 $815,650 $1,223,475* 2017 Super Conforming Loan Amounts (available 12/2/16) Continental US Alaska and Hawaii Units Minimum Loan Maximum Loan Minimum Loan Maximum Loan 1 $424,101 $636,150 $636,151 $954,225 2 $543,001 $814,500 $814,501 $1,221,750* 3 $656,351 $984,525 $984,526 $1,476,775* 4 $815,651 $1,223,475* Ineligible Ineligible Permanent High Cost area the maximum potential loan limits for designated high-cost areas. Actual loan limits are established for each county (or equivalent) and the loan limits for specific high-cost areas may be lower. The original balance of a Mortgage must not exceed the maximum loan limit for the specific areas in which the mortgage premises is located. For specific loan limits for each high cost area, as released by the Federal Housing Finance Agency visit http://www.fhfa.gov/DataTools/Downloads/Pages/Conforming-Loan-Limits.aspx *Maximum Loan Amount in all cases may not exceed $1,000,000. -

An Overview of the Housing Finance System in the United States
An Overview of the Housing Finance System in the United States Updated January 18, 2017 Congressional Research Service https://crsreports.congress.gov R42995 An Overview of the Housing Finance System in the United States Summary When making a decision about housing, a household must choose between renting and owning. Multiple factors, such as a household’s financial status and expectations about the future, influence the decision. Few people who decide to purchase a home have the necessary savings or available financial resources to make the purchase on their own. Most need to take out a loan. A loan that uses real estate as collateral is typically referred to as a mortgage. A potential borrower applies for a loan from a lender in what is called the primary market. The lender underwrites, or evaluates, the borrower and decides whether and under what terms to extend a loan. Different types of lenders, including banks, credit unions, and finance companies (institutions that lend money but do not accept deposits), make home loans. The lender requires some additional assurance that, in the event that the borrower does not repay the mortgage as promised, it will be able to sell the home for enough to recoup the amount it is owed. Typically, lenders receive such assurance through a down payment, mortgage insurance, or a combination of the two. Mortgage insurance can be provided privately or through a government guarantee. After a mortgage is made, the borrower sends the required payments to an entity known as a mortgage servicer, which then remits the payments to the mortgage holder (the mortgage holder can be the original lender or, if the mortgage is sold, an investor). -
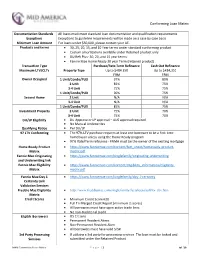
Conforming Loan Matrix
Conforming Loan Matrix Documentation Standards All loans must meet standard loan documentation and qualification requirements Exceptions Exceptions to guideline requirements will be made on a case by case basis Minimum Loan Amount For loans under $50,000, please contact your AE. Products and terms 30, 25, 20, 15, and 10 Year terms under standard conforming product Custom amortizations available under Retained product only DU Refi Plus- 30, 20, and 15 year terms Fannie Mae Home Ready 30 year Term (retained product) Transaction Type Purchase/Rate Term Refinance Cash Out Refinance Maximum LTV/CLTV Property Type Up to $484,350 Up to $484,350 FRM FRM Owner Occupied 1 Unit/Condo/PUD 97% 80% 2 Unit 85% 75% 3-4 Unit 75% 75% 1 Unit/Condo/PUD 90% 75% Second Home 2 Unit N/A N/A 3-4 Unit N/A N/A 1 Unit/Condo/PUD 85% 75% Investment Property 2 Unit 75% 70% 3-4 Unit 75% 70% DU/LP Eligibility DU Approve or LP approval – AUS approval required No Manual Underwrites Qualifying Ratios Per DU/LP 97 LTV Conforming The 97% LTV purchase requires at least one borrower to be a first-time homebuyer unless using the Home Ready program 97% Rate/Term refinance - FNMA must be the owner of the existing mortgage Home Ready Product https://www.fanniemae.com/content/fact_sheet/homeready-product- Matrix matrix.pdf Fannie Mae Originating https://www.fanniemae.com/singlefamily/originating-underwriting and Underwriting link Fannie Mae Eligibility https://www.fanniemae.com/content/eligibility_information/eligibility- Matrix matrix.pdf Fannie Mae Day 1 https://www.fanniemae.com/singlefamily/day-1-certainty -

Mortgage Rates
09/29/2021 10:07 AM Conventional Mortgage Loans for Primary & Secondary Residences Fixed Rate - Serviced by NEFCU Loan Term Rate Points APR Payment Per $1,000 30 Year 3.000% 0.00% 3.023% $4.22 30 Year Low Cost* 3.375% 0.00% 3.398% $4.42 20 Year 2.750% 0.00% 2.782% $5.42 20 Year Low Cost* 3.250% 0.00% 3.283% $5.67 15 Year 2.250% 0.00% 2.291% $6.55 15 Year Low Cost* 2.750% 0.00% 2.792% $6.79 10 Year 2.375% 0.00% 2.436% $9.37 30 Year 100% Financing 3.250% 0.00% 3.273% $4.35 Adjustable Rate Mortgage (ARM) - Serviced by NEFCU Loan Term Rate Points APR Payment Per $1,000 3/1 ARM 1 YR T-Bill; Margin 2.875; Caps 2/6 2.750% 0.00% 2.952% $4.08 3/3 ARM 3 YR T-Bill; Margin 2.875; Caps 2/6 2.875% 0.00% 3.300% $4.15 5/1 ARM 1 YR T-Bill; Margin 2.875; Caps 2/6 2.625% 0.00% 2.883% $4.02 5/5 ARM 5 YR T-Bill; Margin 2.75; Caps 2/6 3.000% 0.00% 3.459% $4.22 7/1 ARM 1 YR T-Bill; Margin 2.875; Caps 2/6 2.875% 0.00% 2.960% $4.15 10/1 ARM 1 YR T-Bill; Margin 2.875, Caps 2/6 3.125% 0.00% 3.099% $4.28 15/15 ARM 10 YR T-Bill; Margin 2.875; Cap 6 3.250% 0.00% 3.499% $4.35 5/1 ARM 1st Time Homebuyer - 1 YR T-Bill; Margin 2.875; Caps 2/5 2.500% 0.00% 2.841% $3.95 5/5 ARM 1st Time Homebuyer - 5 YR T-Bill; Margin 2.75; Caps 2/5 2.875% 0.00% 3.415% $4.15 7/1 ARM 1st Time Homebuyer - 1 YR T-Bill; Margin 2.875; Caps 2/5 2.750% 0.00% 2.903% $4.08 7/1 ARM 100% Financing 1 YR T-Bill; Margin 2.875; Caps 2/5 2.875% 0.00% 2.960% $4.15 10/1 ARM 1st Time Homebuyer - 1 YR T-Bill; Margin 2.875; Caps 2/5 3.000% 0.00% 3.023% $4.22 10/1 ARM 100% Financing 1 YR T-Bill; Margin 2.875; -

U.S. Department of Treasury Housing Reform Plan
U.S. Department of the Treasury Housing Reform Plan Pursuant to the Presidential Memorandum Issued March 27, 2019 SEPTEMBER 2019 TABLE OF CONTENTS I. SUMMARY 1 II. BACKGROUND 4 III. DEFINING A LIMITED ROLE FOR THE FEDERAL GOVERNMENT 12 A. Clarifying Existing Government Support 12 B. Support of Single-Family Mortgage Lending 16 C. Support of Multifamily Mortgage Lending 19 D. Additional Support for Affordable Housing 21 E. Ending the Conservatorships 26 IV. PROTECTING TAXPAYERS AGAINST BAILOUTS 28 A. Capital and Liquidity Requirements 28 B. Resolution Framework 31 C. Retained Mortgage Portfolios 31 D. Credit Underwriting Parameters 33 V. PROMOTING COMPETITION IN THE HOUSING FINANCE SYSTEM 34 A. Leveling the Playing Field 34 B. Competitive Secondary Market 40 C. Competitive Primary Market 42 VI. CONCLUSION 44 I. SUMMARY Housing Finance Reform Goals On March 27, 2019, President Donald J. Trump issued a Presidential Memorandum (the “Presidential Memorandum”) directing the Secretary of the Treasury to develop a plan for administrative and legislative reforms to achieve the following housing reform goals: (i) ending the conservatorships of the Government-sponsored enterprises (each, a “GSE”) upon the completion of specified reforms; (ii) facilitating competition in the housing finance market; (iii) establishing regulation of the GSEs that safeguards their safety and soundness and minimizes the risks they pose to the financial stability of the United States; and (iv) providing that the Federal Government is properly compensated for any explicit or implicit support it provides to the GSEs or the secondary housing finance market. This plan includes legislative and administrative reforms to achieve each of these goals. -

Chapter 3. the VA Loan and Guaranty Overview
VA Pamphlet 26-7, Revised Chapter 3: The VA Loan and Guaranty Chapter 3. The VA Loan and Guaranty Overview In this Chapter This chapter contains the following topics. Topic Topic Name See Page 1 Basic Elements of a VA-Guaranteed Loan 3-2 2 Eligible Loan Purposes 3-5 3 Maximum Loan 3-7 4 Maximum Guaranty on VA Loans 3-10 5 Occupancy 3-12 6 Interest Rates 3-16 7 Discount Points 3-17 8 Maturity 3-19 9 Amortization 3-20 10 Eligible Geographic Locations for the Secured Property 3-22 11 What Does a VA Guaranty Mean to the Lender? 3-23 12 Post-Guaranty Issues 3-26 3-1 VA Pamphlet 26-7, Revised Chapter 3: The VA Loan and Guaranty 1. Basic Elements of a VA-Guaranteed Loan Change Date November 8, 2012, Change 21 • This section has been updated to remove a hyperlink and make minor grammatical edits. a. General rules The following table provides general rules and information critical to understanding a VA loan guaranty. Exceptions and detailed explanations have been omitted. Instead, a reference to the section in this handbook that addresses each subject is provided. Subject Explanation Section Maximum Loan VA has no specified dollar amount(s) for the “maximum 3 of this Amount loan.” The maximum loan amount depends upon: chapter • the reasonable value of the property indicated on the Notice of Value (NOV), and • the lenders needs in terms of secondary market requirements. Downpayment No downpayment is required by VA unless the purchase price 3 of this exceeds the reasonable value of the property, or the loan is a chapter Graduated Payment Mortgage (GPM). -

FHFA Clls Faqs
FHFA Conforming Loan Limits FAQs (updated June 2021) https://www.fhfa.gov/CLLs Overview 1. What are the Conforming Loan Limits (CLLs)? The maximum loan amount for mortgages that can be acquired by Fannie Mae or Freddie Mac. Mortgages above this limit are known as jumbo loans. The CLLs are set by the Federal Housing Finance Agency (FHFA) on an annual basis and vary geographically, using guidelines specified in the Housing and Economic Recovery Act of 2008 (HERA) and as modified in subsequent legislation. More information is provided on the FHFA CLLs webpage at https:/www.fhfa.gov/CLLs. 2. When do new CLLs become effective? At the end of each November, FHFA updates the CLLs based on rules set forth in HERA. The CLLs take effect a month later on January 1st. 3. How are CLLs calculated? Loan limit increases reflect the year-over-year percentage change in the FHFA House Price Index® (HPI) for the United States. The formula is based on the third quarter (Q3) and can be written: (current year Q3 FHFA HPI - prior year Q3 FHFA HPI) / (prior year Q3 FHFA HPI) which is converted to percentage terms. For example, the 2021 limits were computed as: Percentage Change = (2020Q3 HPI – 2019Q3 HPI) / 2019Q3 HPI = (276.84033089 – 257.72651365)/257.72651365 = 7.41631777 percent HERA requires that the baseline loan limit be adjusted each year to reflect changes in the national average home price. In October 2015, FHFA published a Final Notice in the Federal Register specifying that limits would be adjusted using the seasonally adjusted, expanded-data (EXP) version of the FHFA House Price Index® (FHFA HPI®). -
MPF® Glossary
MPF® Glossary Unless a different definition is specifically provided, the following words and phrases shall have the meanings specified below when they are used in the Guides. Actual Credit The sum of Loan Level Credit Enhancement amounts for each Mortgage Enhancement Loan and the Pool Level Credit Enhancement for the same Mortgage Loans in the Master Commitment. Actual/Actual A remittance type that requires the servicer to remit to the investor only the actual interest due (if it is collected from borrowers) and the actual principal payments collected from borrowers. Affiliate Any and all individuals, corporations or organizations which control, are controlled by or are under common control with the Person. All Risk Coverage Property insurance covering loss arising from any fortuitous cause except those that are specifically excluded by the policy itself. Applicable Agreement The PFI Agreement entered into by a Member or similar agreement entered into by a non-Member, and any other agreement that creates the relationship between an entity and an MPF Bank, permitting such entity to participate in the MPF Program, either as an Originator and/or as a Servicer. Applicable Laws All federal, state and local laws, ordinances, rules, regulations and orders, and any applicable decree, injunction, judgment, order, formal interpretation, guidance, or ruling issued by a court or governmental entity applicable to the origination, holding, sale or servicing of Mortgages, whether performed as an agent, principal, independent contractor or vendor. Applicable