DOCSLIB.ORG

DYNAMIC SOARING UAV GLIDERS by Jeffrey H. Koessler

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
DYNAMIC SOARING UAV GLIDERS by Jeffrey H. Koessler Dynamic Soaring UAV Gliders Item Type text; Electronic Dissertation Authors Koessler, Jeffrey H. Publisher The University of Arizona. Rights Copyright © is held by the author. Digital access to this material is made possible by the University Libraries, University of Arizona. Further transmission, reproduction or presentation (such as public display or performance) of protected items is prohibited except with permission of the author. Download date 07/10/2021 13:32:45 Link to Item http://hdl.handle.net/10150/627980 DYNAMIC SOARING UAV GLIDERS by Jeffrey H. Koessler __________________________ Copyright © Jeffrey H. Koessler 2018 A Dissertation Submitted to the Faculty of the DEPARTMENT OF AEROSPACE & MECHANICAL ENGINEERING In Partial Fulfillment of the Requirements For the Degree of DOCTOR OF PHILOSOPHY WITH A MAJOR IN AEROSPACE ENGINEERING In the Graduate College THE UNIVERSITY OF ARIZONA 2018 THEUNIVERSITY OF ARIZONA GRADUATE COLLEGE Date: 01 May 2018 RIZONA 2 STATEMENT BY AUTHOR This dissertation has been submitted in partial fulfillment of the requirements for an advanced degree at the University of Arizona and is deposited in the University Library to be made available to borrowers under rules of the Library. Brief quotations from this dissertation are allowable without special permission, provided that an accurate acknowledgement of the source is made. Requests for permission for extended quotation from or reproduction of this manuscript in whole or in part may be granted by the copyright holder. SIGNED: Jeffrey H. Koessler 3 Acknowledgments This network of mentors, colleagues, friends, and family is simply amazing! Many thanks to... ...My advisor Prof. Fasel for enduring my arguments and crazy ideas about the dynamics of soaring. ...My committee members for time investment, positive feedback, and most of all: encouragement. ...The University of Arizona and AME department for a dynamic environment of discovery. ...Prof. Sanfelice for turning fireflies into synchronizing oscillators and pointing me to dynamic soaring. ...Prof. Gross for my first flight in real glider, acceleration pushing me down, and my lunch almost up. ...Quinton H, Andrew D, and Bear V for believing in me 10 years ago with letters of recommendation. ...Jini K and Janae G for keeping me progressing on track and through all the administrative hoops. ...My 21 students during 4 years of Senior Design soaring projects, and Nik K for “Go big or go home”. ...The Hybrid Dynamics & Controls Lab group: Malladi B, Sean A, Yuchun L, Jun C, Alex J, Pablo N, and Ryan J for teamwork and lively arguments over a multitude of projects, exams, and problem sets. ...Malladi B for getting us past written & oral quals through countless hours of practice exam sessions. ...Brian H for our 2 AM phone calls on HW sets and projects while our growing families slept unawares. ...Chad R, Alex J, and Chris L for collaborating on projects that really made lasting impressions on me. ...Co-workers Stephen W, Neal C, Tim M, Chris M, Chris W, Drew W, Jason F, Cody M, Cody T, Jon O, Paul M, Jake E , Mike T... and many others for enduring my countless persistent questions, comments, and interruptions... in particular Stephen, fate placing his office near mine, for bearing the brunt of it. ...Marc W for his excellent, and simultaneous, driving and videoing skills during daring flight launches. ...My parents and siblings for continually believing that after every milestone, something better is ahead. ...Our three kids for believing in their dad, and left to wonder what a normal family must be like. ...My dearest Stephanie for countless hours missed while on projects, test flights, research, and deadlines. ...Last but not in the least- Thanks to all the pillars and researchers of dynamic soaring, and now potential collaborators. Acknowledging the contributions of the past- and looking towards a dynamic future! ~ ~ many thanks to all of you ~ ~ 4 To Trevor, Annika, and Gordon- our dear children who have tolerated a silly dad- Whatever paths your futures hold: life is a journey, with a destination. To all my family who have given unending support and encouragement to press on- I couldn’t have done it without you- thanks for the boundless provisions. To Stephanie- for allowing this crazy idea to be born 10 years ago, and seeing it through to fruition- I can’t wait for our next chapter in life to begin! “My life is in the Master’s hands to purify and mould; When tested, tried, I’m satisfied I shall come forth as gold!” 5 Table of Contents List of Figures 11 Abstract 15 Nomenclature 16 Chapter 1: Introduction to Dynamic Soaring 17 Chapter Introduction 17 Historical Perspective 17 Static Soaring 20 Dynamic Soaring 24 Flight Experiments 27 Motivation and Novel Contributions 31 Chapter 2: Dynamic Soaring Framework 33 Chapter Introduction 33 Aerodynamic Models 33 Wind Gradient Models 35 Dynamic Soaring Equations of Motion 40 6 Dynamic Soaring Energy 42 Chapter 3: Using Airspeed for Kinetic Energy 44 Chapter Introduction 44 Heuristic Assumptions Summary 44 HA1- A universal inertial reference does not exist- terrestrial earth is not uniquely “inertial” 45 HA2- An infinite choice of reference frames for EoM analyses and simulations are valid 46 HA3- Appropriate choice of KE velocity reference applies to aircraft flying in all conditions 47 HA4- By definition Lift cannot influence airspeed, Drag always opposes airspeed 50 HA5- Aircraft cannot distinguish between locally equivalent spatial and temporal gradients 52 HA6- KE computed from airspeed in a wind-fixed reference frame yields useful energy 54 HA7- Velocity gradients are responsible for useful energy gain in DS, not downwind turns 56 Consequences of Reference Frame Choice 57 7 C1- Source of Dynamic Soaring Energy 58 C2- Roles of Lift and Drag Forces in Energy Rates 58 C3- Exchange Between Potential Energy and Kinetic Energy Forms 59 C4- Kinetic Energy Rates as Used in Flight Control Algorithms 60 Conclusion 60 Chapter 4: Steady State Analysis 62 Chapter Introduction 62 Definition of Steady State Dynamic Soaring in an Airspeed Reference Context 62 Modeling Assumptions 63 Case 1: Steady State Descent in No Wind 64 Case 2: Steady State Descent in a Horizontal Linear Gradient of Horizontal Wind 66 Case 3: Steady State Assent in a Vertical Linear Gradient of Horizontal Wind 68 Case 4: Steady State Descent in a Vertical Linear Gradient of Horizontal Wind 71 8 Case 5: Steady State Flight in Uniform Accelerating Wind 71 Equivalence in Dynamic Soaring Scenarios 73 Dynamic Soaring Sink Polar Surface 73 Chapter 5: Reverse Kinematics Simulation 75 Chapter Introduction 75 Dynamic Soaring Framework Review 75 Typical Dynamic Soaring Simulations 77 Overview of Reverse Kinematics Simulation 79 Three-Dimensional Trajectory Formulation 80 Reverse Kinematics Algorithm 81 Example: Inclined Circular Trajectory 83 Conclusion 86 Chapter 6: Conclusions and Future Research 88 Chapter Introduction 88 Summary of Novel Contributions 89 Future Research and Applications 90 9 Appendix A: Dynamic Soaring Reference Frame 92 References 99 10 List of Figures Figure 1.1: Thermal and orographic lift 17 Figure 1.2: Rayleigh cycle for dynamic soaring 18 Figure 1.3: L-23 Super Blanik with NASA SENIOR ShWOOPIN team 19 Figure 1.4: 2008 Montague Cross Country Challenge teams 20 Figure 1.5: Typical tandem glider 21 Figure 1.6: SBXC glider sink polar 21 Figure 1.7: Sources of thermal lift 22 Figure 1.8: Sources of ridge lift 23 Figure 1.9: Sources of wave lift 23 Figure 1.10: Boundary layer wind profile 24 Figure 1.11: Albatross flight trajectory in boundary layer wind gradient 25 Figure 1.12: Circular hover 26 Figure 1.13: Snaking hover 26 Figure 1.14: Circular zoom 26 Figure 1.15: Circumnavigation 26 Figure 1.16: Valenta Weasel 2.1 m glider 28 11 Figure 1.17: Valenta Sharon 4.2 m glider 28 Figure 1.18: UAV architecture block diagram 29 Figure 1.19: Autopilot, sensors, telemetry, and control 29 Figure 1.20: Typical screenshot of mission planner GCS real-time telemetry 30 Figure 1.21: Arizona winds aloft 30 Figure 1.22: Prediction for ideal dynamic soaring conditions at test site 30 Figure 1.23: Sharon 4.2 m UAV glider 32 Figure 2.1: Air relative velocity and applied forces 34 Figure 2.2: Circular flow 38 Figure 2.3: Boundary layer wind profile 39 Figure 2.4: Horizontal wind speed vs. height 39 Figure 2.5: Horizontal wind gradient vs. height 39 Figure 2.6: Dynamic soaring forces 40 Figure 3.1: Air-relative velocity and applied forces 46 Figure 3.2: Four forces in flight 50 Figure 3.3: Dynamic soaring forces 53 12 Figure 4.1: Dynamic soaring forces 63 Figure 4.2a: Linear horizontal gradient (source) 66 Figure 4.2b: Linear horizontal gradient (sink) 66 Figure 4.2c: Radial horizontal gradient (source) 66 Figure 4.2d: Radial horizontal gradient (sink) 66 Figure 4.3: Vertical linear gradient of horizontal wind 68 Figure 4.4: Sink polar shift for heavier weight 70 Figure 4.5: Dynamic soaring sink polar surface 74 Figure 5.1: Air relative velocity and applied forces 76 Figure 5.2: Wind velocity vs height 78 Figure 5.3: Wind gradient vs height 78 Figure 5.4: Inclined circular trajectory 84 Figure 5.5: Bank angle vs trajectory position parameter for inclined circular trajectory 85 Figure 5.6: Specific energy vs trajectory position parameter for inclined circular trajectory 85 13 Figure 5.7: Load factor vs trajectory position parameter for inclined circular trajectory 86 Figure A.1: Glider descending in calm wind 92 Figure A.2: Glider ascending through accelerating wind-fixed reference frame 93 Figure A.3: Glider ascending through accelerating wind-fixed reference frame with addition of rotated DS reference frame notation (red) 94 Figure A.4: Glider descending in rotated DS reference frame 95 Figure A.5: Glider descending in simplified rotated DS reference frame 96 14 ABSTRACT Dynamic soaring in the atmospheric boundary layer of a vertical variation of horizontal winds over arbitrary terrain offers small unmanned aerial vehicle gliders the ability to greatly expand mission operations while also extending endurance.
Load more

Recommended publications
  • Understanding the Value of Arts & Culture | the AHRC Cultural Value
    Understanding the value of arts & culture The AHRC Cultural Value Project Geoffrey Crossick & Patrycja Kaszynska 2 Understanding the value of arts & culture The AHRC Cultural Value Project Geoffrey Crossick & Patrycja Kaszynska THE AHRC CULTURAL VALUE PROJECT CONTENTS Foreword 3 4. The engaged citizen: civic agency 58 & civic engagement Executive summary 6 Preconditions for political engagement 59 Civic space and civic engagement: three case studies 61 Part 1 Introduction Creative challenge: cultural industries, digging 63 and climate change 1. Rethinking the terms of the cultural 12 Culture, conflict and post-conflict: 66 value debate a double-edged sword? The Cultural Value Project 12 Culture and art: a brief intellectual history 14 5. Communities, Regeneration and Space 71 Cultural policy and the many lives of cultural value 16 Place, identity and public art 71 Beyond dichotomies: the view from 19 Urban regeneration 74 Cultural Value Project awards Creative places, creative quarters 77 Prioritising experience and methodological diversity 21 Community arts 81 Coda: arts, culture and rural communities 83 2. Cross-cutting themes 25 Modes of cultural engagement 25 6. Economy: impact, innovation and ecology 86 Arts and culture in an unequal society 29 The economic benefits of what? 87 Digital transformations 34 Ways of counting 89 Wellbeing and capabilities 37 Agglomeration and attractiveness 91 The innovation economy 92 Part 2 Components of Cultural Value Ecologies of culture 95 3. The reflective individual 42 7. Health, ageing and wellbeing 100 Cultural engagement and the self 43 Therapeutic, clinical and environmental 101 Case study: arts, culture and the criminal 47 interventions justice system Community-based arts and health 104 Cultural engagement and the other 49 Longer-term health benefits and subjective 106 Case study: professional and informal carers 51 wellbeing Culture and international influence 54 Ageing and dementia 108 Two cultures? 110 8.
    [Show full text]
  • Soaring Weather
    Chapter 16 SOARING WEATHER While horse racing may be the "Sport of Kings," of the craft depends on the weather and the skill soaring may be considered the "King of Sports." of the pilot. Forward thrust comes from gliding Soaring bears the relationship to flying that sailing downward relative to the air the same as thrust bears to power boating. Soaring has made notable is developed in a power-off glide by a conven­ contributions to meteorology. For example, soar­ tional aircraft. Therefore, to gain or maintain ing pilots have probed thunderstorms and moun­ altitude, the soaring pilot must rely on upward tain waves with findings that have made flying motion of the air. safer for all pilots. However, soaring is primarily To a sailplane pilot, "lift" means the rate of recreational. climb he can achieve in an up-current, while "sink" A sailplane must have auxiliary power to be­ denotes his rate of descent in a downdraft or in come airborne such as a winch, a ground tow, or neutral air. "Zero sink" means that upward cur­ a tow by a powered aircraft. Once the sailcraft is rents are just strong enough to enable him to hold airborne and the tow cable released, performance altitude but not to climb. Sailplanes are highly 171 r efficient machines; a sink rate of a mere 2 feet per second. There is no point in trying to soar until second provides an airspeed of about 40 knots, and weather conditions favor vertical speeds greater a sink rate of 6 feet per second gives an airspeed than the minimum sink rate of the aircraft.
    [Show full text]
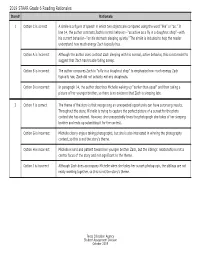
  • 2019 STAAR Grade 6 Reading Rationales Item# Rationale
    2019 STAAR Grade 6 Reading Rationales Item# Rationale 1 Option C is correct A simile is a figure of speech in which two objects are compared using the word “like” or “as.” In line 14, the author contrasts Zach’s normal behavior—“as active as a fly in a doughnut shop”—with his current behavior—“on his stomach sleeping quietly.” The simile is included to help the reader understand how much energy Zach typically has. Option A is incorrect Although the author does contrast Zach sleeping with his normal, active behavior, this is not meant to suggest that Zach has trouble falling asleep. Option B is incorrect The author compares Zach to “a fly in a doughnut shop” to emphasize how much energy Zach typically has; Zach did not actually eat any doughnuts. Option D is incorrect In paragraph 14, the author describes Michelle waking up “earlier than usual” and then taking a picture of her younger brother, so there is no evidence that Zach is sleeping late. 2 Option F is correct The theme of the story is that recognizing an unexpected opportunity can have surprising results. Throughout the story, Michelle is trying to capture the perfect picture of a sunset for the photo contest she has entered. However, she unexpectedly loves the photograph she takes of her sleeping brother and ends up submitting it for the contest. Option G is incorrect Michelle clearly enjoys taking photographs, but she is also interested in winning the photography contest, so this is not the story’s theme. Option H is incorrect Michelle is kind and patient toward her younger brother Zach, but the siblings’ relationship is not a central focus of the story and not significant to the theme.
    [Show full text]
  • Days & Hours for Social Distance Walking Visitor Guidelines Lynden
    53 22 D 4 21 8 48 9 38 NORTH 41 3 C 33 34 E 32 46 47 24 45 26 28 14 52 37 12 25 11 19 7 36 20 10 35 2 PARKING 40 39 50 6 5 51 15 17 27 1 44 13 30 18 G 29 16 43 23 PARKING F GARDEN 31 EXIT ENTRANCE BROWN DEER ROAD Lynden Sculpture Garden Visitor Guidelines NO CLIMBING ON SCULPTURE 2145 W. Brown Deer Rd. Do not climb on the sculptures. They are works of art, just as you would find in an indoor art Milwaukee, WI 53217 museum, and are subject to the same issues of deterioration – and they endure the vagaries of our harsh climate. Many of the works have already spent nearly half a century outdoors 414-446-8794 and are quite fragile. Please be gentle with our art. LAKES & POND There is no wading, swimming or fishing allowed in the lakes or pond. Please do not throw For virtual tours of the anything into these bodies of water. VEGETATION & WILDLIFE sculpture collection and Please do not pick our flowers, fruits, or grasses, or climb the trees. We want every visitor to be able to enjoy the same views you have experienced. Protect our wildlife: do not feed, temporary installations, chase or touch fish, ducks, geese, frogs, turtles or other wildlife. visit: lynden.tours WEATHER All visitors must come inside immediately if there is any sign of lightning. PETS Pets are not allowed in the Lynden Sculpture Garden except on designated dog days.
    [Show full text]
  • Alexander 2013 Principles-Of-Animal-Locomotion.Pdf
    .................................................... Principles of Animal Locomotion Principles of Animal Locomotion ..................................................... R. McNeill Alexander PRINCETON UNIVERSITY PRESS PRINCETON AND OXFORD Copyright © 2003 by Princeton University Press Published by Princeton University Press, 41 William Street, Princeton, New Jersey 08540 In the United Kingdom: Princeton University Press, 3 Market Place, Woodstock, Oxfordshire OX20 1SY All Rights Reserved Second printing, and first paperback printing, 2006 Paperback ISBN-13: 978-0-691-12634-0 Paperback ISBN-10: 0-691-12634-8 The Library of Congress has cataloged the cloth edition of this book as follows Alexander, R. McNeill. Principles of animal locomotion / R. McNeill Alexander. p. cm. Includes bibliographical references (p. ). ISBN 0-691-08678-8 (alk. paper) 1. Animal locomotion. I. Title. QP301.A2963 2002 591.47′9—dc21 2002016904 British Library Cataloging-in-Publication Data is available This book has been composed in Galliard and Bulmer Printed on acid-free paper. ∞ pup.princeton.edu Printed in the United States of America 1098765432 Contents ............................................................... PREFACE ix Chapter 1. The Best Way to Travel 1 1.1. Fitness 1 1.2. Speed 2 1.3. Acceleration and Maneuverability 2 1.4. Endurance 4 1.5. Economy of Energy 7 1.6. Stability 8 1.7. Compromises 9 1.8. Constraints 9 1.9. Optimization Theory 10 1.10. Gaits 12 Chapter 2. Muscle, the Motor 15 2.1. How Muscles Exert Force 15 2.2. Shortening and Lengthening Muscle 22 2.3. Power Output of Muscles 26 2.4. Pennation Patterns and Moment Arms 28 2.5. Power Consumption 31 2.6. Some Other Types of Muscle 34 Chapter 3.
    [Show full text]
  • Design and Flight-Path Simulation of a Dynamic-Soaring UAV
    PhD Dissertations and Master's Theses Summer 7-2021 Design and Flight-Path Simulation of a Dynamic-Soaring UAV Gladston Joseph [email protected] Follow this and additional works at: https://commons.erau.edu/edt Part of the Aerodynamics and Fluid Mechanics Commons, Aeronautical Vehicles Commons, Navigation, Guidance, Control and Dynamics Commons, Other Aerospace Engineering Commons, and the Propulsion and Power Commons Scholarly Commons Citation Joseph, Gladston, "Design and Flight-Path Simulation of a Dynamic-Soaring UAV" (2021). PhD Dissertations and Master's Theses. 599. https://commons.erau.edu/edt/599 This Thesis - Open Access is brought to you for free and open access by Scholarly Commons. It has been accepted for inclusion in PhD Dissertations and Master's Theses by an authorized administrator of Scholarly Commons. For more information, please contact [email protected]. Design and Flight-Path Simulation of a Dynamic-Soaring UAV By Gladston Joseph A Thesis Submitted to the Faculty of Embry-Riddle Aeronautical University In Partial Fulfillment of the Requirements for the Degree of Master of Science in Aerospace Engineering July 2021 Embry-Riddle Aeronautical University Daytona Beach, Florida Daewon Kim 8/3/2021 8/3/2021 8/3/2021 iii ACKNOWLEDGEMENTS “In the beginning God created the heavens and the earth” - Genesis 1:1 NKJV I would like to thank my advisors, Dr. Vladimir Golubev, and Dr. Snorri Gudmundsson for their expertise, guidance and the moral support. I would also like to extend my acknowledgement to Dr. William Mackunis and Dr. Hever Moncayo for their guidance in the development of control laws. My gratitude goes towards my father, Mr.
    [Show full text]
  • July 2000 on the INSIDE
    July 2000 WESTWIND Instructor Kenny Price and Student Eric Lentz (of Williams) with the coveted PASCO Egg ON THE INSIDE PASCO / SSA / Operations / Club Directory .......................................................................................... Page 2-3 Minisafetytips .......................................................................................................................................... Page 6 In Brief ..................................................................................................................................................... Page 6 Year 2000 Sawyer Award Features ........................................................................................................... Page 7 Flying the Electric Winch in Unterwossen ...................................................................................... Page 8 Air Sailing Sports Class Contest ....................................................................................................... Page 10 Air Sailing Sports Class Scores ............................................................................................................... Page 12 Year 2000 Sawyer Award ................................................................................................................... Page 13 A Guide for Submitting Photos to WestWind .................................................................................. Page 13 Classified Ads......................................................................................................................................
    [Show full text]
  • Closing the Loop in Dynamic Soaring
    AIAA 2014-0263 AIAA SciTech 13-17 January 2014, National Harbor, Maryland AIAA Guidance, Navigation, and Control Conference Closing the Loop in Dynamic Soaring John J. Bird∗ and Jack W. Langelaany The Pennsylvania State University, University Park, PA 16802 USA Corey Montella,z John Spletzer,x and Joachim Grenestedt{ Lehigh University, Bethlehem, PA 18015 USA This paper examines closed-loop dynamic soaring by small autonomous aircraft. Wind field estimation, trajectory planning, and path-following control are integrated into a sys- tem to enable dynamic soaring. The control architecture is described, performance of components of the architecture is assessed in Monte Carlo simulation, and the trajectory constraints imposed by existing hardware are described. Hardware in the loop simulation using a Piccolo SL autopilot module are used to examine the feasibility of dynamic soaring in the shear layer behind a ridge, and the limitations of the system are described. Results show that even with imperfect path following dynamic soaring is possible with currently existing hardware. The effect of turbulence is assessed through the addition of Dryden turbulence in the simulation environment. I. Introduction For certain missions, such as ocean monitoring, dynamic soaring has the potential to greatly enhance range and endurance of small uavs. Albatrosses and petrels are similar in both size and weight to small unmanned aircraft, and they routinely employ dynamic soaring to travel thousands of kilometers.1,2,3 Deittert et al. show that the probability of winds that permit dynamic soaring by small uavs exceeds 50% in the southern oceans, and this probability is roughly 90% for albatrosses.4 The difference is because albatrosses can descend to very low altitude (dragging a wingtip in the water) and uavs must maintain a significant safety margin.
    [Show full text]
  • May 1983 Issue of Soaring Magazine
    Cambridge Introduces The New M KIV NA V Used by winners at the: 15M French Nationals U.S. 15M Nationals U.S. Open Nationals British Open Nationals Cambridge is pleased to announce the Check These Features: MKIV NAV, the latest addition to the successful M KIV System. Digital Final Glide Computer with • "During Glide" update capability The MKIV NAV, by utilizing the latest Micro­ • Wind Computation capability computer and LCD technology, combines in • Distance-to-go Readout a single package a Speed Director, a • Altitude required Readout 4-Function Audio, a digital Averager, and an • Thermalling during final glide capability advanced, digital Final Glide Computer. Speed Director with The MKIV NAV is designed to operate with the MKIV Variometer. It will also function • Own LCD "bar-graph" display with a Standard Cambridge Variometer. • No effect on Variometer • No CRUISE/CLIMB switching The MKIV NAV is the single largest invest­ ment made by Cambridge in state-of-the-art Digital 20 second Averager with own Readout technology and represents our commitment Relative Variometer option to keeping the U.S. in the forefront of soar­ ing instrumentation. 4·Function Audio Altitude Compensation Cambridge Aero Instruments, Inc. Microcomputer and Custom LCD technology 300 Sweetwater Ave. Bedford, MA 01730 Single, compact package, fits 80mm (31/8") Tel. (617) 275·0889; TWX# 710·326·7588 opening Mastercharge and Visa accepted BUSINESS. MEMBER G !TORGLIDING The JOURNAL of the SOARING SOCIETYof AMERICA Volume 47 • Number 5 • May 1983 6 THE 1983 SSA INTERNATIONAL The Soaring Society of America is a nonprofit SOARING CONVENTION organization of enthusiasts who seek to foster and promote all phases of gliding and soaring on a national and international basis.
    [Show full text]
  • Weather Forecasting for Soaring Flight
    Weather Forecasting for Soaring Flight Prepared by Organisation Scientifique et Technique Internationale du Vol aVoile (OSTIV) WMO-No. 1038 2009 edition World Meteorological Organization Weather. Climate _ Water WMO-No. 1038 © World Meteorological Organization, 2009 The right of publication in print, electronic and any other form and in any language is reserved by WMO. Short extracts from WMO publications may be reproduced without authorization, provided that the complete source is clearly indicated. Editorial correspondence and requests to publish, repro­ duce or translate this publication in part or in whole should be addressed to: Chairperson, Publications Board World Meteorological Organization (WMO) 7 his, avenue de la Paix Tel.: +41 (0) 22 7308403 P.O. Box 2300 Fax: +41 (0) 22 730 80 40 CH-1211 Geneva 2, Switzerland E-mail: [email protected] ISBN 978-92-63-11038-1 NOTE The designations employed in WMO publications and the presentation of material in this publication do not imply the expression of any opinion whatsoever on the part of the Secretariat of WMO concerning the legal status of any country, territory, city or area, or of its authorities, or concerning the delimitation of its frontiers or boundaries. Opinions expressed in WMO publications are those of the authors and do not necessarily reflect those of WMO. The mention of specific companies or products does not imply that they are endorsed or recommended by WMO in preference to others of a similar nature which are not mentioned or advertised. CONTENTS Page FOREWORD....................................................................................................................................... v INTRODUCTION vii CHAPTER 1. ATMOSPHERIC PROCESSES ENABLING SOARING FLIGHT...................................... 1-1 1.1 Overview.................................................................................................................................
    [Show full text]
  • The Design and Testing of an Airfoil for Winglet on Low-Speed Aircraft
    Extracting Energy from Atmospheric Turbulence with Flight Tests Chinmay K. Patel Acuity Technologies Inc. Menlo Park, CA 94025 USA [email protected] Hak-Tae Lee University of California, Santa Cruz Moffett Field, CA 94035 USA [email protected] and Ilan M. Kroo Stanford University Stanford, CA 94305 USA [email protected] Accepted by the XXIX OSTIV Congress, Lüsse-Berlin, Germany, 6 August – 13 August 2008 Abstract Birds frequently use the energy present in the atmosphere to conserve their energy while flying. Although en- ergy in the form of thermal updrafts is routinely used by pilots of full-scale and model sailplanes, the energy in atmospheric turbulence has not been utilized to its full potential. This paper deals with the design of simple control laws to extract energy from atmospheric turbulence. A simulation-based optimization procedure to de- sign control laws for energy extraction from realistic turbulence was developed, leading to about 36% average energy savings for a ‘bird-sized’ glider. Flight test results are presented to demonstrate the energy extraction concept and validate the predicted savings. The emergence of ultra-light sailplanes has opened up the possibility of utilizing this form of ‘gust-soaring’ for a class of manned sailplanes, and the concepts presented in this paper can serve as a background for understanding and applying the techniques to extract energy from atmospheric turbulence. Nomenclature t Time bref Reference span V0 Nominal aircraft speed cref Reference chord Vair Airspeed CD Coefficient of
    [Show full text]
  • On the Size and Flight Diversity of Giant Pterosaurs, the Use of Birds As Pterosaur Analogues and Comments on Pterosaur Flightlessness
    On the Size and Flight Diversity of Giant Pterosaurs, the Use of Birds as Pterosaur Analogues and Comments on Pterosaur Flightlessness Mark P. Witton1*, Michael B. Habib2 1 School of Earth and Environmental Sciences, University of Portsmouth, Portsmouth, United Kingdom, 2 Department of Sciences, Chatham University, Pittsburgh, Pennsylvania, United States of America Abstract The size and flight mechanics of giant pterosaurs have received considerable research interest for the last century but are confused by conflicting interpretations of pterosaur biology and flight capabilities. Avian biomechanical parameters have often been applied to pterosaurs in such research but, due to considerable differences in avian and pterosaur anatomy, have lead to systematic errors interpreting pterosaur flight mechanics. Such assumptions have lead to assertions that giant pterosaurs were extremely lightweight to facilitate flight or, if more realistic masses are assumed, were flightless. Reappraisal of the proportions, scaling and morphology of giant pterosaur fossils suggests that bird and pterosaur wing structure, gross anatomy and launch kinematics are too different to be considered mechanically interchangeable. Conclusions assuming such interchangeability—including those indicating that giant pterosaurs were flightless—are found to be based on inaccurate and poorly supported assumptions of structural scaling and launch kinematics. Pterosaur bone strength and flap-gliding performance demonstrate that giant pterosaur anatomy was capable of generating sufficient
    [Show full text]