DOCSLIB.ORG

Metallicity Variations and Conduction in the Intracluster Medium

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Metallicity Variations and Conduction in the Intracluster Medium Metallicity Variations and Conduction in the Intracluster Medium THIS DISSERTATION IS SUBMITTED FOR THE DEGREE OF DOCTOR OF PHILOSOPHY March 2003 Roger Glenn Morris INSTITUTE OF ASTRONOMY & ROBINSON COLLEGE UNIVERSITY OF CAMBRIDGE For J. A. M. and J. K. M. DECLARATION I hereby declare that my thesis entitled Metallicity Variations and Conduction in the Intracluster Medium is not substantially the same as any that I have submitted for a degree or diploma or other qualification at any other University. I further state that no part of my thesis has already been or is being concurrently submitted for any such degree, diploma or other qualification. This dissertation is the result of my own work and includes nothing which is the outcome of work done in collaboration except where specifically indicated in the text. Those parts of this thesis which have been published or accepted for publication are as follows. Sections of Chapters 2 and 4 were published as: • Morris R. G., Fabian A. C., 2003, MNRAS, 338, 824. Some of the issues discussed in Chapter 4 were presented in preliminary form in: • Morris R. G., Fabian A. C., 2002, in Matteucci and Fusco-Femiano (2002), pp. 85–90. Work on thermal conduction (Chapter 5) has benefited from discussions with Lisa Voigt, published • as: Fabian A. C., Voigt L. M., Morris R. G., 2002b, MNRAS, 335, L71. Various figures throughout the text are reproduced from the work of other authors, for illustration or discussion. Such figures are always credited in the associated caption. This thesis contains fewer than 60,000 words. R. Glenn Morris Cambridge, 10th March 2003 v SUMMARY This thesis focuses mainly on an investigation of possible explanations for the lack of low-temperature emission lines seen in recent X-ray spectra of cooling flow clusters. I consider two main hypotheses. Firstly, I examine the idea that the metals in the intracluster medium might be distributed inhomoge- neously on small, as yet unresolved scales. I make a theoretical analysis of the effects that such a metal distribution would have on the X-ray spectra of cooling plasmas such as are found in the centres of galaxy clusters. Using the standard isobaric cooling flow model, I quantify the suppression in low-temperature line emission that can be achieved in this way. Different species are found to behave in different fashion, as governed by the temperature dependence of their equivalent widths. I go on to describe my implementation of a one-dimensional Lagrangian numerical scheme that can be used to model the intracluster medium in either a single-phase or multi-phase mode. Synthetic X-ray observations can be produced and analysed using standard tools. This scheme is used to investigate the spatial and temporal evolution of simulated clusters with small-scale metallicity variations. I stress the effects on the observed spectra, and the deductions that would be made from them. I find that such metal distributions may give rise to interesting effects in observed abundance profiles, in that apparent abundance gradients with central abundance drops and off-centre peaks, similar to those seen in several real clusters, can be produced. The importance of observational testing of this hypothesis is stressed. Secondly, I study some of the possible effects of efficient thermal conduction in the intracluster plasma. The numerical code is modified to include the effects of thermal conduction. The level of con- ductivity is controlled by the structure of the cluster magnetic field, and I include a simple parametrization to represent this. The influence of conduction on the evolution of the temperature profile for high- and low-temperature clusters is demonstrated, as well as its ability to delay the onset of cooling in cluster cores over a wide range of cluster parameters. The simulations highlight the difficulty in constructing stable solutions to the cooling flow problem based on thermal conduction, but do show that the properties of clusters are such that conduction is potentially an important process for their evolution. vii ACKNOWLEDGEMENTS∗ Or, “This is all your fault, you know” Well, here we are. To be honest, there were times when I wondered if I’d ever get to this point. That I have done is largely due, I think, to the people listed below. This is poor recompense for putting up with me, but I hope to make it up to you all in the future. It’s been a long three-and-some years, and what I’ve learnt about astronomy is far outweighed by the other things you have taught me. I may go on for too long here, but what the hell, nobody’s forcing you to read this. If I were to write fully what I owe to all of you, it would be a second thesis, but one is quite enough. It’s a cliche´ to say that this thesis wouldn’t exist without my supervisor, Andy Fabian, but that doesn’t make it any less true. Thanks to him for suggesting many interesting lines of inquiry, and for tolerating my appalling slowness in following them up. Thanks to Andy Amos for putting up with me during my A-levels, for appreciating the value of sarcasm, and for not complaining too much when I turned my back on biology. I’d like to thank/blame Alastair Edge for getting me started in the field of X-ray astronomy in the first place, all those years ago. It was him who made me think this seemed like it could be a fun thing to do. Alastair is also responsible for my firm belief that unfeasibly large tea mugs and astronomy should go hand in hand. I’m also grateful for the observing trip to IRAM Granada, to see how the other half lives. Thanks to Thomas Hove Pedersen for helping me get through my undergraduate years, though I fear our personalities were too similar to be good for either of us. Still, another pair of hands to steady the mortar is always useful. It looks like I haven’t learnt your “get out of Cambridge” lesson yet Tom, so you’ll have to keep explaining it to me. Thanks to Felipe Menanteau for being one of those to welcome me to the Hoyle 19 family on my arrival to the IoA, and for being a part of the project to educate me with the palabra del d´ıa. I’m sorry I turned out to be such a poor pupil. To Meghan Gray for a lot of sensible advice, many emails, some fun conversations, and generally for taking an interest. As another one of the original senior figures (sorry!) of H19 she contributed enormously to the great (and much missed) atmosphere. Thank you also Meghan for some much-needed support during some difficult times. To Mateusz “the Disco King” Ruszkowski for his shared appreciation of Desperados beer, and for managing to teach me one word of Polish. Sadly your dancing shoes remain unfilled in the Group. Thanks to Richard Wilman, who despite having the singular misfortune in life to have been born a Yorkshireman, remains a thoroughly decent bloke. To Raquel Morales for an awful lot of things, including some very civilised lunches, a lot of fruit tea, some fine walks and many good conversations. Heartfelt thanks for being a pillar of the small but select group that tried to keep me sane, and apologies for making it such a difficult job at times. Thanks to Andrea Merloni and Alessandra Corchia for tolerating so well my decidedly non-Italian temperament, some good parties, and for making it possible for me to see Rome. To Enrico Ramirez Ruiz and Kristin Truse I owe more than I can say. Thank you for many fine dinners, for your tolerance and understanding, for Mexico, for putting up with your unsociable flatmate, ∗The OED recommends ªacknowledgmentsº. What is the world coming to? ix x Acknowledgements for Borges, and above all for your friendship. El deseo de expresar gratitud aventaja a mi capacidad de enunciarlo, desgraciadamente en cualquier idioma. To Jon Gair, Fraser Clarke and Dave Gittins must go collective thanks for many hours of slacking, as the co-inventors of the truly beautiful concepts of Pre-tea Tea, Pre-pre-tea Tea, Post-tea Tea. I’m sorry we never got round to the twenty-four hour tea-a-thon, but we surely put the training in. Thanks guys for making life at the IoA enjoyable, and for some good nights at the St. Radegund. Individually, thanks to Jon for trying to keep me fit with the occasional bout of squash, to Dave for being a games programmer extraordinaire, and to Fraser for inviting me over to watch his TV (several times), and buying a round (once). Dave gets another mention as a fellow webcomic-devotee, and the most prolific (OK, only) suggester of features for “the script”. Thanks Dave, and also Colin Frayn and Fraser, for sharing my obsession (to some degree), and having at least a vague idea of what I was talking about in my references to Bobbins et al. My thanks to Poshak “The Shak” Gandhi for the gifts of his friendship, and his bicycle. The former carries me farther than the latter ever will. I dread to think what impression of British culture we’ve left you with Poshak, and how badly we must have corrupted your vocabulary. To Richard Barker, for a lot of things over a lot of years, including many fine walks in the Lakes that provide me with fond memories. I’m looking forward to many more in the future. Thanks also for being a man of letters Richard, and reminding me of the virtues of pen and paper.
Load more

Recommended publications
  • INVESTIGATING ACTIVE GALACTIC NUCLEI with LOW FREQUENCY RADIO OBSERVATIONS By
    INVESTIGATING ACTIVE GALACTIC NUCLEI WITH LOW FREQUENCY RADIO OBSERVATIONS by MATTHEW LAZELL A thesis submitted to The University of Birmingham for the degree of DOCTOR OF PHILOSOPHY School of Physics & Astronomy College of Engineering and Physical Sciences The University of Birmingham March 2015 University of Birmingham Research Archive e-theses repository This unpublished thesis/dissertation is copyright of the author and/or third parties. The intellectual property rights of the author or third parties in respect of this work are as defined by The Copyright Designs and Patents Act 1988 or as modified by any successor legislation. Any use made of information contained in this thesis/dissertation must be in accordance with that legislation and must be properly acknowledged. Further distribution or reproduction in any format is prohibited without the permission of the copyright holder. Abstract Low frequency radio astronomy allows us to look at some of the fainter and older synchrotron emission from the relativistic plasma associated with active galactic nuclei in galaxies and clusters. In this thesis, we use the Giant Metrewave Radio Telescope to explore the impact that active galactic nuclei have on their surroundings. We present deep, high quality, 150–610 MHz radio observations for a sample of fifteen predominantly cool-core galaxy clusters. We in- vestigate a selection of these in detail, uncovering interesting radio features and using our multi-frequency data to derive various radio properties. For well-known clusters such as MS0735, our low noise images enable us to see in improved detail the radio lobes working against the intracluster medium, whilst deriving the energies and timescales of this event.
    [Show full text]
  • 10. Scientific Programme 10.1
    10. SCIENTIFIC PROGRAMME 10.1. OVERVIEW (a) Invited Discourses Plenary Hall B 18:00-19:30 ID1 “The Zoo of Galaxies” Karen Masters, University of Portsmouth, UK Monday, 20 August ID2 “Supernovae, the Accelerating Cosmos, and Dark Energy” Brian Schmidt, ANU, Australia Wednesday, 22 August ID3 “The Herschel View of Star Formation” Philippe André, CEA Saclay, France Wednesday, 29 August ID4 “Past, Present and Future of Chinese Astronomy” Cheng Fang, Nanjing University, China Nanjing Thursday, 30 August (b) Plenary Symposium Review Talks Plenary Hall B (B) 8:30-10:00 Or Rooms 309A+B (3) IAUS 288 Astrophysics from Antarctica John Storey (3) Mon. 20 IAUS 289 The Cosmic Distance Scale: Past, Present and Future Wendy Freedman (3) Mon. 27 IAUS 290 Probing General Relativity using Accreting Black Holes Andy Fabian (B) Wed. 22 IAUS 291 Pulsars are Cool – seriously Scott Ransom (3) Thu. 23 Magnetars: neutron stars with magnetic storms Nanda Rea (3) Thu. 23 Probing Gravitation with Pulsars Michael Kremer (3) Thu. 23 IAUS 292 From Gas to Stars over Cosmic Time Mordacai-Mark Mac Low (B) Tue. 21 IAUS 293 The Kepler Mission: NASA’s ExoEarth Census Natalie Batalha (3) Tue. 28 IAUS 294 The Origin and Evolution of Cosmic Magnetism Bryan Gaensler (B) Wed. 29 IAUS 295 Black Holes in Galaxies John Kormendy (B) Thu. 30 (c) Symposia - Week 1 IAUS 288 Astrophysics from Antartica IAUS 290 Accretion on all scales IAUS 291 Neutron Stars and Pulsars IAUS 292 Molecular gas, Dust, and Star Formation in Galaxies (d) Symposia –Week 2 IAUS 289 Advancing the Physics of Cosmic
    [Show full text]
  • Counting Gamma Rays in the Directions of Galaxy Clusters
    A&A 567, A93 (2014) Astronomy DOI: 10.1051/0004-6361/201322454 & c ESO 2014 Astrophysics Counting gamma rays in the directions of galaxy clusters D. A. Prokhorov1 and E. M. Churazov1,2 1 Max Planck Institute for Astrophysics, Karl-Schwarzschild-Strasse 1, 85741 Garching, Germany e-mail: [email protected] 2 Space Research Institute (IKI), Profsouznaya 84/32, 117997 Moscow, Russia Received 6 August 2013 / Accepted 19 May 2014 ABSTRACT Emission from active galactic nuclei (AGNs) and from neutral pion decay are the two most natural mechanisms that could establish a galaxy cluster as a source of gamma rays in the GeV regime. We revisit this problem by using 52.5 months of Fermi-LAT data above 10 GeV and stacking 55 clusters from the HIFLUCGS sample of the X-ray brightest clusters. The choice of >10 GeV photons is optimal from the point of view of angular resolution, while the sample selection optimizes the chances of detecting signatures of neutral pion decay, arising from hadronic interactions of relativistic protons with an intracluster medium, which scale with the X-ray flux. In the stacked data we detected a signal for the central 0.25 deg circle at the level of 4.3σ. Evidence for a spatial extent of the signal is marginal. A subsample of cool-core clusters has a higher count rate of 1.9 ± 0.3 per cluster compared to the subsample of non-cool core clusters at 1.3 ± 0.2. Several independent arguments suggest that the contribution of AGNs to the observed signal is substantial, if not dominant.
    [Show full text]
  • New Type of Black Hole Detected in Massive Collision That Sent Gravitational Waves with a 'Bang'
    New type of black hole detected in massive collision that sent gravitational waves with a 'bang' By Ashley Strickland, CNN Updated 1200 GMT (2000 HKT) September 2, 2020 <img alt="Galaxy NGC 4485 collided with its larger galactic neighbor NGC 4490 millions of years ago, leading to the creation of new stars seen in the right side of the image." class="media__image" src="//cdn.cnn.com/cnnnext/dam/assets/190516104725-ngc-4485-nasa-super-169.jpg"> Photos: Wonders of the universe Galaxy NGC 4485 collided with its larger galactic neighbor NGC 4490 millions of years ago, leading to the creation of new stars seen in the right side of the image. Hide Caption 98 of 195 <img alt="Astronomers developed a mosaic of the distant universe, called the Hubble Legacy Field, that documents 16 years of observations from the Hubble Space Telescope. The image contains 200,000 galaxies that stretch back through 13.3 billion years of time to just 500 million years after the Big Bang. " class="media__image" src="//cdn.cnn.com/cnnnext/dam/assets/190502151952-0502-wonders-of-the-universe-super-169.jpg"> Photos: Wonders of the universe Astronomers developed a mosaic of the distant universe, called the Hubble Legacy Field, that documents 16 years of observations from the Hubble Space Telescope. The image contains 200,000 galaxies that stretch back through 13.3 billion years of time to just 500 million years after the Big Bang. Hide Caption 99 of 195 <img alt="A ground-based telescope's view of the Large Magellanic Cloud, a neighboring galaxy of our Milky Way.
    [Show full text]
  • Active Galactic Nucleus Feedback in Clusters of Galaxies
    Active galactic nucleus feedback in clusters of galaxies Elizabeth L. Blantona,1, T. E. Clarkeb, Craig L. Sarazinc, Scott W. Randalld, and Brian R. McNamarad,e aInstitute for Astrophysical Research and Astronomy Department, Boston University, 725 Commonwealth Avenue, Boston, MA 02215; bNaval Research Laboratory, 455 Overlook Avenue SW, Washington, DC 20375; cDepartment of Astronomy, University of Virginia, P.O. Box 400325, Charlottesville, VA 22904-4325; dHarvard-Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge, MA 02138; eDepartment of Physics and Astronomy, University of Waterloo, Waterloo, ON N2L 2G1, Canada; and Perimeter Institute for Theoretical Physics, 31 Caroline Street, North Waterloo, Ontario N2L 2Y5, Canada Edited by Neta A. Bahcall, Princeton University, Princeton, NJ, and approved February 22, 2010 (received for review December 3, 2009) Observations made during the last ten years with the Chandra there is little cooling. This is seen in the temperature profiles as X-ray Observatory have shed much light on the cooling gas in well as high resolution spectroscopy. An important early result the centers of clusters of galaxies and the role of active galactic from XMM-Newton high resolution spectra from cooling flows nucleus (AGN) heating. Cooling of the hot intracluster medium was that the emission lines from cool gas were not present at in cluster centers can feed the supermassive black holes found the expected levels, and the spectra were well-fitted by a cooling in the nuclei of the dominant cluster galaxies leading to AGN out- flow model with a low temperature cutoff (7, 8). This cutoff is bursts which can reheat the gas, suppressing cooling and large typically one-half to one-third of the average cluster temperature, amounts of star formation.
    [Show full text]
  • Lecture 22 Clusters of Galaxies II
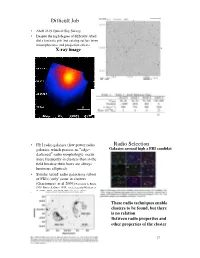
    Difficult Job ! • Abell 2319 Optical Sky Survey ! • Despite the high degree of difficulty Abell did a fantastic job- but catalog suffers from incompleteness and projection effects ! X-ray image! 26! • FR I radio galaxies (low power radio Radio Selection ! galaxies, which possess an edge- Galaxies around high z FRI candidates ! darkened radio morphology) occur more frequently in clusters than in the field because their hosts are always luminous ellipticals ! • Similar 'tailed' radio galaxies(a subset of FRIs) 'only' occur in clusters (Giacintucci et al 2009) Fomalont & Bridle 1978; Burns & Owen 1979; more recently Blanton et al. 2000, 2001 and 2003; Smolcic et al. 2007; Kantharia et al. 2009).! These radio techniques enable ! clusters to be found, but there is no relation! Between radio properties and other properties of the cluster ! 27! Cluster Formation ! • Cluster mergers are thought to be the prime mechanism of massive cluster formation in a hierarchical universe (White and Frenk 1991) ! • the most energetic events in the universe since the big bang. These mergers with infall velocities of ~2000 15 km/s and total masses of 10 M! have a kinetic energy of 1065 ergs. ! • The shocks and structures generated in the merger have a important influence on cluster shape, luminosity and evolution and may generate large fluxes of relativistic particles! 28! Numerical Simulation of a Merger ! • X-ray contours with kT in color, dark matter distribution, velocity vectors and how the two gas components mix (0.3 and 3.5Gyr after closest approach) ! •Roettiger, Stone and Mushotzky 1998 first detailed simulations of a merger- trying to match A754! 29! X-ray Images of Mergers ! A85! • A754 (Henry et al 2004) pressure and x-ray intensity images ! 30! • Movie from http:// www.mult idark.org/ MultiDark /pages/ ImagesMo vies.jsp! • made by G.
    [Show full text]
  • Selected Galaxy Clusters at 0 < Z <
    THE EVOLUTION OF THE INTRACLUSTER MEDIUM METALLICITY IN SUNYAEV ZEL’DOVICH- SELECTED GALAXY CLUSTERS AT 0 < Z < 1.5 The MIT Faculty has made this article openly available. Please share how this access benefits you. Your story matters. Citation McDonald, M., et al. “THE EVOLUTION OF THE INTRACLUSTER MEDIUM METALLICITY IN SUNYAEV ZEL’DOVICH-SELECTED GALAXY CLUSTERS AT 0 < z < 1.5.” The Astrophysical Journal, vol. 826, no. 2, July 2016, p. 124. © 2016. The American Astronomical Society As Published http://dx.doi.org/10.3847/0004-637X/826/2/124 Publisher American Astronomical Society Version Final published version Citable link http://hdl.handle.net/1721.1/116266 Terms of Use Article is made available in accordance with the publisher's policy and may be subject to US copyright law. Please refer to the publisher's site for terms of use. The Astrophysical Journal, 826:124 (11pp), 2016 August 1 doi:10.3847/0004-637X/826/2/124 © 2016. The American Astronomical Society. All rights reserved. THE EVOLUTION OF THE INTRACLUSTER MEDIUM METALLICITY IN SUNYAEV ZEL’DOVICH-SELECTED GALAXY CLUSTERS AT 0<z<1.5 M. McDonald1, E. Bulbul1, T. de Haan2, E. D. Miller1, B. A. Benson3,4,5, L. E. Bleem4,6, M. Brodwin7, J. E. Carlstrom4,5, I. Chiu8,9, W. R. Forman10, J. Hlavacek-Larrondo11, G. P. Garmire12, N. Gupta8,9,13, J. J. Mohr8,9,13, C. L. Reichardt14, A. Saro8,9, B. Stalder15, A. A. Stark10, and J. D. Vieira16 1 Kavli Institute for Astrophysics and Space Research, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA 02139, USA; [email protected] 2 Department of Physics, University of California, Berkeley, CA 94720, USA 3 Fermi National Accelerator Laboratory, Batavia, IL 60510-0500, USA 4 Kavli Institute for Cosmological Physics, University of Chicago, 5640 South Ellis Avenue, Chicago, IL 60637, USA 5 Department of Astronomy and Astrophysics, University of Chicago, 5640 South Ellis Avenue, Chicago, IL 60637, USA 6 Argonne National Laboratory, 9700 S.
    [Show full text]
  • Measuring Redshifts Using X-Ray Spectroscopy of Galaxy Clusters: Results from Chandra Data and Future Prospects
    A&A 529, A65 (2011) Astronomy DOI: 10.1051/0004-6361/201016236 & c ESO 2011 Astrophysics Measuring redshifts using X-ray spectroscopy of galaxy clusters: results from Chandra data and future prospects H. Yu1,2,P.Tozzi2,3, S. Borgani4,3,P.Rosati5,andZ.-H.Zhu1 1 Department of Astronomy, Beijing Normal University, Beijing 100875, PR China e-mail: [email protected] 2 INAF Osservatorio Astronomico di Trieste, via G.B. Tiepolo 11, 34143 Trieste, Italy 3 INFN – National Institute for Nuclear Physics, Trieste, Italy 4 Dipartimento di Fisica dell’Università di Trieste, via G.B. Tiepolo 11, 34131 Trieste, Italy 5 ESO – European Southern Observatory, Karl-Schwarzschild Str. 2, 85748 Garching b. Munchen, Germany Received 30 November 2010 / Accepted 9 February 2011 ABSTRACT Context. The ubiquitous presence of the Fe line complex in the X-ray spectra of galaxy clusters offers the possibility of measuring their redshift without resorting to spectroscopic follow-up observations. In practice, the blind search of the Fe line in X-ray spectra is adifficult task and is affected not only by limited S/N (particularly at high redshift), but also by several systematic errors, associated with varying Fe abundance values, ICM temperature gradients, and instrumental characteristics. Aims. We assess the accuracy with which the redshift of galaxy clusters can be recovered from an X-ray spectral analysis of Chandra archival data. We present a strategy to compile large surveys of clusters whose identification and redshift measurement are both based on X-ray data alone. Methods. We apply a blind search for K-shell and L-shell Fe line complexes in X-ray cluster spectra using Chandra archival obser- vations of galaxy clusters.
    [Show full text]
  • Bruggen's Slide Presentation
    PARTICLE ACCELERATION ON COSMOLOGICAL SCALES @HambObs MARCUS BRÜGGEN Abell 2744 Optical 1 Mpc Pearce+ (2017) Abell 2744 X-rays: intracluster mediumOptical (ICM) 1 Mpc Pearce+ (2017) Abell 2744 Radio: cosmicX-rays: rays intracluster (CR) + magnetic mediumOptical fields(ICM) 1 Mpc Pearce+ (2017) Abell 2744 Radio: cosmicX-rays: rays intracluster (CR) + magnetic mediumOptical fields(ICM) ~μGauss 1 Mpc Pearce+ (2017) Abell 2744 Radio: cosmicX-rays: rays intracluster (CR) + magnetic mediumOptical fields(ICM) ~μGauss radio spectra slope: spectral index (α) “flat” “steep” Diffuse cluster radio emission has a steep 1 Mpc spectrum Pearce+ (2017) DIFFUSE CLUSTER EMISSION JVLA 1-4 GHz latest reviews: Feretti+2012; Brunetti & Jones 2014 Pearce et al. (2017) 1.0 Mpc X-rays: 0.5-2.0 keV RELIC HALOS HALO • Mpc sizes, centrally located • Unpolarized Tailed radio galaxy • X-ray luminosity radio power correlation foreground AGN • Found in disturbed clusters DIFFUSE CLUSTER EMISSION JVLA 1-4 GHz latest reviews: Feretti+2012; Brunetti & Jones 2014 Pearce et al. (2017) 1.0 Mpc X-rays: 0.5-2.0 keV RELICS RELIC • Mpc sizes, cluster outskits • Elongated, filamentary morphologies • Polarized • Found in disturbed clusters HALOS HALO • Mpc sizes, centrally located • Unpolarized Tailed radio galaxy • X-ray luminosity radio power correlation foreground AGN • Found in disturbed clusters HOW DO YOU ACCELERATE PARTICLES? FERMI (1949): SCATTER OFF MOVING CLOUDS. VERY SLOW (V2/C2) BECAUSE CLOUDS BOTH APPROACH AND RECEDE IN SHOCKS, ACCELERATION IS 1ST ORDER IN V/C BECAUSE FLOWS
    [Show full text]
  • Galaxy / Cluster Ecosystem
    Galaxy / Cluster Ecosystem Ming Sun (University of Alabama in Huntsville)‏ P. Jachym (AIAS, Czech Republic); S. Sivanandam (U. of Toronto); J. Scharwaechter, F. Combes, P. Salome (LERMA); P. Nulsen, W. Forman, C. Jones, A. Vikhlinin, B. Zhang (CfA); M. Fumagalli (Durham); J. Sanders, M. Fossati (MPE); M. Donahue, M. Voit (MSU); C. Sarazin (UVa); A. Fabian (Cambridge); R. Canning, N. Werner (Stanford); E. Roediger (Hamburg); D. Vir Lal (NCRA); L. Cortese (Swinburne); J. Kenney (Yale) Why study galaxy / cluster ecosystem ? 1) Galaxies inject energy into the intracluster medium (ICM), with AGN outflows, galactic winds, galaxy motion etc. 2) Galaxies also dump heavy elements and magnetic field in the ICM. 3) Clusters also change galaxies, e.g., density - morphology (or SFR) relation, with e.g., ram pressure stripping and harassment. 4) Great examples to study transport processes (conductivity and viscosity) Summary Ram pressure Stripping Environment stripped tails Conduction UMBHs B Draping (multi-phase Radio AGN Turbulence gas and SF) You have heard a lot of discussions on thermal coronae of early-type galaxies in this workshop. What about early-type galaxies‏in‏clusters?‏Are‏they‏“naked”‏without‏gas?‏‏--- No firm detections of coronae in hot clusters before Chandra ! You have heard a lot of discussions on thermal coronae of early-type galaxies in this workshop. What about early-type galaxies‏in‏clusters?‏Are‏they‏“naked”‏without‏gas?‏‏--- No firm detections of coronae in hot clusters before Chandra ! Vikhlinin + 2001 You have heard a lot of discussions on thermal coronae of early-type galaxies in this workshop. What about early-type galaxies‏in‏clusters?‏Are‏they‏“naked”‏without‏gas?‏‏--- No firm detections of coronae in hot clusters before Chandra ! Vikhlinin + 2001 Later more embedded coronae discovered (Yamasaki+2002; Sun+2002, 2005, 2006) and the first sample in Sun+2007 You have heard a lot of discussions on thermal coronae of early-type galaxies in this workshop.
    [Show full text]
  • LERMA REPORT V1.1 PART II
    LERMA 2007-2012 Contractualisation vague D Results vol. 3 Bibliography (version 1.1) Conception graphique S. Cabrit Sect. 3. Bibliography Sect. 3. Bibliography A detailed analysis of the lab's production would need a huge investment to be truly meaningful, so we better stay with simple facts. The table below shows the distribution among years and thematic poles of refereed and non refereed publications during the reporting period. Year ACL Publ. Pole 1 Pole 2 Pole 3 Pole 4 Overlap 2007 119 37 45 27 18 8 2008 133 40 57 25 21 10 2009 116 27 59 17 17 4 2010 214 50 112 25 87 60 2011 197 81 71 53 51 59 2012 77 31 29 15 10 8 Total 856 266 373 162 204 149 Table 2: Count of refereed publications from the ADS database Year Publis ACL Pôle 1 Pôle 2 Pôle 3 Pôle 4 Overlap 2007 2409 988 798 220 502 99 2008 2239 633 1166 222 290 72 2009 1489 341 852 119 196 19 2010 3283 1394 1412 213 1548 1284 2011 3035 2331 637 1345 1434 2712 2012 239 183 62 20 2 28 Totaux 12694 5870 4927 2139 3972 4214 Table 3: Count of the citations to the refereed publications from the ADS database. Beware the incompleteness of citations to plasma physics, molecular physics, remote sensing and engineering papers in this database Year ACL Publ. Pole 1 Pole 2 Pole 3 Pole 4 2007 20 27 18 8 28 2008 17 16 20 9 14 2009 13 13 14 7 12 2010 15 28 13 9 18 2011 15 29 9 25 28 2012 3 6 2 1 0 Totaux 15 22 13 13 19 Table 4: Average citation rate for the same publications Sect.
    [Show full text]
  • Cool Gas in Brightest Cluster Galaxies
    Cool Gas in Brightest Cluster Galaxies Cool Gas in Brightest Cluster Galaxies Proefschrift ter verkrijging van de graad van Doctor aan de Universiteit Leiden, op gezag van de Rector Magnificus prof. mr. P.F. van der Heijden, volgens besluit van het College voor Promoties te verdedigen op donderdag 6 oktober 2011 klokke 11.15 uur door Johannes Bernardus Raymond Oonk geboren te Hengelo in 1981 Promotiecommissie Promotor: Prof. dr. W. Jaffe Overige leden: Dr. J. Brinchmann Prof. dr. A. C. Fabian (University of Cambridge) Prof. dr. F. P. Israel Prof. dr. K. Kuijken ISBN: 978-94-6191-031-8 Contents vii Contents Page Chapter 1. Introduction 1 1.1 Galaxy Clusters ................................... 1 1.2 Cool-core Clusters ................................. 1 1.3 ThehotgasatT>107 K .............................. 2 1.4 ThecoolgasatT<104 K .............................. 2 1.5 This Thesis ..................................... 3 1.6 Outlook ....................................... 5 Chapter 2. Warm Molecular Gas in Abell 2597 and Sersic 159-03 7 2.1 Introduction .................................... 8 2.1.1 This project ................................. 10 2.2 Observations and reduction ............................ 10 2.2.1 Near Infrared Data ............................. 10 2.2.2 X-ray Data ................................. 13 2.2.3 Radio Data ................................. 14 2.3 Abell 2597 – Gas Distribution ........................... 14 2.3.1 Molecular gas ................................ 15 2.3.2 Ionised gas ................................. 16 2.4 Abell 2597 – Gas Kinematics ........................... 16 2.4.1 Molecular gas ................................ 17 2.4.2 Ionised gas ................................. 18 2.4.3 Filaments .................................. 18 2.5 Sersic 159-03 – Gas Distribution .......................... 19 2.5.1 Molecular gas ................................ 20 2.5.2 Ionised gas ................................. 20 2.6 Sersic 159-03 – Gas Kinematics .......................... 21 2.6.1 Molecular gas ...............................
    [Show full text]