Photon Shot Noise Dephasing in the Strong-Dispersive Limit of Circuit QED
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

10S Johnson-Nyquist Noise Masatsugu Sei Suzuki Department of Physics, SUNY at Binghamton (Date: January 02, 2011)
Chapter 10S Johnson-Nyquist noise Masatsugu Sei Suzuki Department of Physics, SUNY at Binghamton (Date: January 02, 2011) Johnson noise Johnson-Nyquist theorem Boltzmann constant Parseval relation Correlation function Spectral density Wiener-Khinchin (or Khintchine) Flicker noise Shot noise Poisson distribution Brownian motion Fluctuation-dissipation theorem Langevin function ___________________________________________________________________________ John Bertrand "Bert" Johnson (October 2, 1887–November 27, 1970) was a Swedish-born American electrical engineer and physicist. He first explained in detail a fundamental source of random interference with information traveling on wires. In 1928, while at Bell Telephone Laboratories he published the journal paper "Thermal Agitation of Electricity in Conductors". In telecommunication or other systems, thermal noise (or Johnson noise) is the noise generated by thermal agitation of electrons in a conductor. Johnson's papers showed a statistical fluctuation of electric charge occur in all electrical conductors, producing random variation of potential between the conductor ends (such as in vacuum tube amplifiers and thermocouples). Thermal noise power, per hertz, is equal throughout the frequency spectrum. Johnson deduced that thermal noise is intrinsic to all resistors and is not a sign of poor design or manufacture, although resistors may also have excess noise. http://en.wikipedia.org/wiki/John_B._Johnson 1 ____________________________________________________________________________ Harry Nyquist (February 7, 1889 – April 4, 1976) was an important contributor to information theory. http://en.wikipedia.org/wiki/Harry_Nyquist ___________________________________________________________________________ 10S.1 Histrory In 1926, experimental physicist John Johnson working in the physics division at Bell Labs was researching noise in electronic circuits. He discovered random fluctuations in the voltages across electrical resistors, whose power was proportional to temperature. -
![Arxiv:2003.13216V1 [Cs.CV] 30 Mar 2020](https://docslib.b-cdn.net/cover/3269/arxiv-2003-13216v1-cs-cv-30-mar-2020-263269.webp)
Arxiv:2003.13216V1 [Cs.CV] 30 Mar 2020
Learning to Learn Single Domain Generalization Fengchun Qiao Long Zhao Xi Peng University of Delaware Rutgers University University of Delaware [email protected] [email protected] [email protected] Abstract : Source domain(s) <latexit sha1_base64="glUSn7xz2m1yKGYjqzzX12DA3tk=">AAAB8nicjVDLSsNAFL3xWeur6tLNYBFclaQKdllw47KifUAaymQ6aYdOJmHmRiihn+HGhSJu/Rp3/o2TtgsVBQ8MHM65l3vmhKkUBl33w1lZXVvf2Cxtlbd3dvf2KweHHZNkmvE2S2SieyE1XArF2yhQ8l6qOY1Dybvh5Krwu/dcG5GoO5ymPIjpSIlIMIpW8vsxxTGjMr+dDSpVr+bOQf4mVViiNai894cJy2KukElqjO+5KQY51SiY5LNyPzM8pWxCR9y3VNGYmyCfR56RU6sMSZRo+xSSufp1I6exMdM4tJNFRPPTK8TfPD/DqBHkQqUZcsUWh6JMEkxI8X8yFJozlFNLKNPCZiVsTDVlaFsq/6+ETr3mndfqNxfVZmNZRwmO4QTOwINLaMI1tKANDBJ4gCd4dtB5dF6c18XoirPcOYJvcN4+AY5ZkWY=</latexit> <latexit sha1_base64="9X8JvFzvWSXuFK0x/Pe60//G3E4=">AAACD3icbVDLSsNAFJ3UV62vqks3g0Wpm5LW4mtVcOOyUvuANpTJZNIOnUzCzI1YQv/Ajb/ixoUibt26829M2iBqPTBwOOfeO/ceOxBcg2l+GpmFxaXllexqbm19Y3Mrv73T0n6oKGtSX/iqYxPNBJesCRwE6wSKEc8WrG2PLhO/fcuU5r68gXHALI8MJHc5JRBL/fxhzyMwpEREjQnuAbuD6AI3ptOx43uEy6I+muT6+YJZMqfA86SckgJKUe/nP3qOT0OPSaCCaN0tmwFYEVHAqWCTXC/ULCB0RAasG1NJPKataHrPBB/EioNdX8VPAp6qPzsi4mk99uy4Mtle//US8T+vG4J7ZkVcBiEwSWcfuaHA4OMkHOxwxSiIcUwIVTzeFdMhUYRCHOEshPMEJ98nz5NWpVQ+LlWvq4VaJY0ji/bQPiqiMjpFNXSF6qiJKLpHj+gZvRgPxpPxarzNSjNG2rOLfsF4/wJA4Zw6</latexit> S S : Target domain(s) <latexit sha1_base64="ssITTP/Vrn2uchq9aDxvcfruPQc=">AAACD3icbVDLSgNBEJz1bXxFPXoZDEq8hI2Kr5PgxWOEJAaSEHonnWTI7Owy0yuGJX/gxV/x4kERr169+TfuJkF8FTQUVd10d3mhkpZc98OZmp6ZnZtfWMwsLa+srmXXN6o2iIzAighUYGoeWFRSY4UkKayFBsH3FF57/YvUv75BY2WgyzQIselDV8uOFECJ1MruNnygngAVl4e8QXhL8Rkvg+ki8Xbgg9R5uzfMtLI5t+COwP+S4oTk2ASlVva90Q5E5KMmocDaetENqRmDISkUDjONyGIIog9drCdUg4+2GY/+GfKdRGnzTmCS0sRH6veJGHxrB76XdKbX299eKv7n1SPqnDRjqcOIUIvxok6kOAU8DYe3pUFBapAQEEYmt3LRAwOCkgjHIZymOPp6+S+p7heKB4XDq8Pc+f4kjgW2xbZZnhXZMTtnl6zEKkywO/bAntizc+88Oi/O67h1ypnMbLIfcN4+ATKRnDE=</latexit> -
Next Topic: NOISE
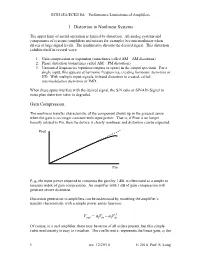
ECE145A/ECE218A Performance Limitations of Amplifiers 1. Distortion in Nonlinear Systems The upper limit of useful operation is limited by distortion. All analog systems and components of systems (amplifiers and mixers for example) become nonlinear when driven at large signal levels. The nonlinearity distorts the desired signal. This distortion exhibits itself in several ways: 1. Gain compression or expansion (sometimes called AM – AM distortion) 2. Phase distortion (sometimes called AM – PM distortion) 3. Unwanted frequencies (spurious outputs or spurs) in the output spectrum. For a single input, this appears at harmonic frequencies, creating harmonic distortion or HD. With multiple input signals, in-band distortion is created, called intermodulation distortion or IMD. When these spurs interfere with the desired signal, the S/N ratio or SINAD (Signal to noise plus distortion ratio) is degraded. Gain Compression. The nonlinear transfer characteristic of the component shows up in the grossest sense when the gain is no longer constant with input power. That is, if Pout is no longer linearly related to Pin, then the device is clearly nonlinear and distortion can be expected. Pout Pin P1dB, the input power required to compress the gain by 1 dB, is often used as a simple to measure index of gain compression. An amplifier with 1 dB of gain compression will generate severe distortion. Distortion generation in amplifiers can be understood by modeling the amplifier’s transfer characteristic with a simple power series function: 3 VaVaVout=−13 in in Of course, in a real amplifier, there may be terms of all orders present, but this simple cubic nonlinearity is easy to visualize. -

Thermal-Noise.Pdf
Thermal Noise Introduction One might naively believe that if all sources of electrical power are removed from a circuit that there will be no voltage across any of the components, a resistor for example. On average this is correct but a close look at the rms voltage would reveal that a "noise" voltage is present. This intrinsic noise is due to thermal fluctuations and can be calculated as may be done in your second year thermal physics course! The main goal of this experiment is to measure and characterize this noise: Johnson noise. In order to measure the intrinsic noise of a component one must first reduce the extrinsic sources of noise, i.e. interference. You have probably noticed that if you touch the input lead to an oscilloscope a large signal appears. Try this now and characterize the signal you see. Note that you are acting as an antenna! Make sure you look at both long time scales, say 10 ms, and shorter time scales, say 1 s. What are the likely sources of the signals you see? You may recall seeing this before in the First Year Laboratory. This interference is characterized by two features. First, the noise voltage is characterized by a spectrum, i.e. the noise voltage Vn ( f ) is a function of frequency. 2 Since noise usually has a time average of zero, the power spectrum Vn ( f ) is specified in each frequency interval df . Second, the measuring instrument is also characterized by a spectral response or bandwidth. In our case the bandwidth of the oscilloscope is from fL =0 (when input is DC coupled) to an upper frequency fH usually noted on the scope (beware of bandwidth limiting switches). -
Noise Is Widespread
NoiseNoise A definition (not mine) Electrical Noise S. Oberholzer and E. Bieri (Basel) T. Kontos and C. Hoffmann (Basel) A. Hansen and B-R Choi (Lund and Basel) ¾ Electrical noise is defined as any undesirable electrical energy (?) T. Akazaki and H. Takayanagi (NTT) E.V. Sukhorukov and D. Loss (Basel) C. Beenakker (Leiden) and M. Büttiker (Geneva) T. Heinzel and K. Ensslin (ETHZ) M. Henny, T. Hoss, C. Strunk (Basel) H. Birk (Philips Research and Basel) Effect of noise on a signal. (a) Without noise (b) With noise ¾ we like it though (even have a whole conference on it) National Center on Nanoscience Swiss National Science Foundation 1 2 Noise may have been added to by ... Introduction: Noise is widespread Noise (audio, sound, HiFi, encodimg, MPEG) Electrical Noise Noise (industrial, pollution) Noise (in electronic circuits) Noise (images, video, encoding) Noise (environment, pollution) it may be in the “source” signal from the start Noise (radio) it may have been introduced by the electronics Noise (economic => theory of pricing with fluctuating it may have been added to by the envirnoment source terms) it may have been generated in your computer Noise (astronomy, big-bang, cosmic background) Noise figure Shot noise Thermal noise for the latter, e.g. sampling noise Quantum noise Neuronal noise Standard quantum limit and more ... 3 4 Introduction: Noise is widespread Introduction (Wikipedia) Noise (audio, sound, HiFi, encodimg, MPEG) Electronic Noise (from Wikipedia) Noise (industrial, pollution) Noise (in electronic circuits) Noise (images, video, encoding) Electronic noise exists in any electronic circuit as a result of random variations in current or voltage caused by the random movement of the Noise (environment, pollution) electrons carrying the current as they are jolted around by thermal energy.energy Noise (radio) The lower the temperature the lower is this thermal noise. -

The Power Spectral Density of Phase Noise and Jitter: Theory, Data Analysis, and Experimental Results by Gil Engel
AN-1067 APPLICATION NOTE One Technology Way • P. O. Box 9106 • Norwood, MA 02062-9106, U.S.A. • Tel: 781.329.4700 • Fax: 781.461.3113 • www.analog.com The Power Spectral Density of Phase Noise and Jitter: Theory, Data Analysis, and Experimental Results by Gil Engel INTRODUCTION GENERAL DESCRIPTION Jitter on analog-to-digital and digital-to-analog converter sam- There are numerous techniques for generating clocks used in pling clocks presents a limit to the maximum signal-to-noise electronic equipment. Circuits include R-C feedback circuits, ratio that can be achieved (see Integrated Analog-to-Digital and timers, oscillators, and crystals and crystal oscillators. Depend- Digital-to-Analog Converters by van de Plassche in the References ing on circuit requirements, less expensive sources with higher section). In this application note, phase noise and jitter are defined. phase noise (jitter) may be acceptable. However, recent devices The power spectral density of phase noise and jitter is developed, demand better clock performance and, consequently, more time domain and frequency domain measurement techniques costly clock sources. Similar demands are placed on the spectral are described, limitations of laboratory equipment are explained, purity of signals sampled by converters, especially frequency and correction factors to these techniques are provided. The synthesizers used as sources in the testing of current higher theory presented is supported with experimental results applied performance converters. In the following section, definitions to a real world problem. of phase noise and jitter are presented. Then a mathematical derivation is developed relating phase noise and jitter to their frequency representation. -

Denoising Autoencoder 10 Autoencoder (Lecun 1987, Bourlard and Kamp, 1988, Hinton and Zemel 1994)
Denoising Wavefront sensor Images with Deep Neural Networks Bartomeu Pou Barcelona Supercomputing Center Polytechnic University of Catalonia 2 Introduction Bartomeu Pou • PhD student in Artificial Intelligence in Barcelona Supercomputing Center and Polytechnic University of Catalonia. • Interested in Machine Learning and its application in Adaptive Optics. 3 Introduction Eduardo Quiñones Damien Gratadour Mario Martín • Barcelona • Australian National University. • Polytechnic University of Supercomputing Center. • LESIA, Observatoire de Paris, Catalonia. Universite PSL, CNRS, Sorbonne Universite. • Universite Paris Diderot. 4 Problem: Noise in the AO Loop 5 Closed-loop Adaptive Optics 6 Closed-loop Adaptive Optics 1. Process WFS info with Center of gravity (cog) method. σ푥(σ푦 퐼 푥,푦 )푥 σ푦(σ푥 퐼 푥,푦 )푦 푆푥 = ; 푆푦 = σ푥 σ푦 퐼 푥,푦 σ푥 σ푦 퐼 푥,푦 푚 = (푆 , 푆 , … , 푆 , 푆 , 푆 , … , 푆 ) 푥1 푥2 푥푛 푦1 푦2 푦푛 7 Closed-loop Adaptive Optics 2. Integrator with gain • Commands that should be applied: 푐 = 푅 푚 • Reduce error by integrating past commands: 퐶푡 = 퐶푡−1 − 푔푐 8 Noise in wavefront sensor subapertures We treat the two main sources of noise in AO: 1. Readout noise on the subaperture detectors. 2. Shot noise due to photon statistics. a) Noise free WFS subaperture image. b) Noise in the subaperture image. cog=(-0.008, -0.028) cog=(0.367, -0.018) 9 Solution: Denoising Autoencoder 10 Autoencoder (LeCun 1987, Bourlard and Kamp, 1988, Hinton and Zemel 1994) 1. Unsupervised learning method based on neural networks. 11 Autoencoder (LeCun 1987, Bourlard and Kamp, 1988, Hinton and Zemel 1994) 1. Unsupervised learning method based on neural networks. -

AN118: Improving ADC Resolution by Oversampling and Averaging
AN118 IMPROVING ADC RESOLUTION BY OVERSAMPLING AND AVERAGING 1. Introduction 2. Key Points Many applications require measurements using an Oversampling and averaging can be used to analog-to-digital converter (ADC). Such increase measurement resolution, eliminating the applications will have resolution requirements need to resort to expensive, off-chip ADCs. based in the signal’s dynamic range, the smallest Oversampling and averaging will improve the SNR and measurement resolution at the cost of increased change in a parameter that must be measured, and CPU utilization and reduced throughput. the signal-to-noise ratio (SNR). For this reason, Oversampling and averaging will improve signal-to- many systems employ a higher resolution off-chip noise ratio for “white” noise. ADC. However, there are techniques that can be 2.1. Sources of Data Converter Noise used to achieve higher resolution measurements and SNR. This application note describes utilizing Noise in ADC conversions can be introduced from oversampling and averaging to increase the many sources. Examples include: thermal noise, resolution and SNR of analog-to-digital shot noise, variations in voltage supply, variation in conversions. Oversampling and averaging can the reference voltage, phase noise due to sampling increase the resolution of a measurement without clock jitter, and noise due to quantization error. The resorting to the cost and complexity of using noise caused by quantization error is commonly expensive off-chip ADCs. referred to as quantization noise. Noise power from This application note discusses how to increase the these sources can vary. Many techniques that may resolution of analog-to-digital (ADC) measure- be utilized to reduce noise, such as thoughtful ments by oversampling and averaging. -
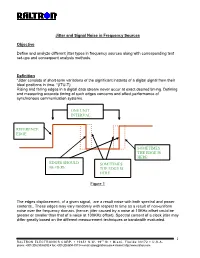
Jitter and Signal Noise in Frequency Sources
Jitter and Signal Noise in Frequency Sources Objective Define and analyze different jitter types in frequency sources along with corresponding test set-ups and consequent analysis methods. Definition “Jitter consists of short-term variations of the significant instants of a digital signal from their ideal positions in time. “(ITU-T) Rising and falling edges in a digital data stream never occur at exact desired timing. Defining and measuring accurate timing of such edges concerns and affect performance of synchronous communication systems. ONE UNIT INTERVAL REFERENCE EDGE SOMETIMES THE EDGE IS HERE EDGES SHOULD SOMETIMES BE HERE THE EDGE IS HERE Figure 1 The edges displacement, of a given signal, are a result noise with both spectral and power contents.. These edges may vary randomly with respect to time as a result of non-uniform noise over the frequency domain. (hence; jitter caused by a noise at 10KHz offset could be greater or smaller than that of a noise at 100KHz offset). Spectral content of a clock jitter may differ greatly based on the different measurement techniques or bandwidth evaluated. 1 RALTRON ELECTRONICS CORP. ! 10651 N.W. 19th St ! Miami, Florida 33172 ! U.S.A. phone: +001(305) 593-6033 ! fax: +001(305)594-3973 ! e-mail: [email protected] ! internet: http://www.raltron.com System Disruptions caused by Jitter Clock recovery mechanisms, in network elements, are used to sample the digital signal using the recovered bit clock. If the digital signal and the clock have identical jitter, the constant jitter error will not affect the sampling instant and therefore no bit errors will arise. -

Quantum Shot Noise Formula (4) Has Been Tested Andrew Steinbach and John Martinis at the US National Experimentally in a Variety of Systems
Quantum Shot Noise Fluctuations in the flow of electrons signal the transition from particle to wave behavior. Published in revised form in Physics Today, May 2003, page 37. Carlo Beenakker & Christian Sch¨onenberger∗ “The noise is the signal” was a saying of Rolf Landauer, Types of electrical noise one of the founding fathers of mesoscopic physics. What he meant is that fluctuations in time of a measurement Not all types of electrical noise are informative. The fluc- can be a source of information that is not present in the tuating voltage over a conductor in thermal equilibrium time-averaged value. A physicist may actually delight in is just noise. It tells us only the value of the temperature noise. T . To get more out of noise one has to bring the electrons out of thermal equilibrium. Before getting into that, let Noise plays a uniquely informative role in connection us say a bit more about thermal noise — also known with the particle-wave duality. It was Albert Einstein as “Johnson-Nyquist noise” after the two physicists who who first realized (in 1909) that electromagnetic fluctu- first studied it in a quantitative way. ations are different if the energy is carried by waves or Thermal noise extends over all frequencies up to the by particles. The magnitude of energy fluctuations scales quantum limit at kT/h. In a typical experiment one fil- linearly with the mean energy for classical waves, but it ters the fluctuations in a band width ∆f around some scales with the square root of the mean energy for clas- frequency f. -

Sources of Phase Noise and Jitter in Oscillators by Ramon Cerda, Crystek Crystals Corporation
PAGE • MARCH 2006 FEATURE ARTICLE WWW.MPDIGEST.COM Sources of Phase Noise and Jitter in Oscillators by Ramon Cerda, Crystek Crystals Corporation he output signal of an oscillator, no matter how good it is, will contain Tall kinds of unwanted noises and signals. Some of these unwanted signals are spurious output frequencies, harmon- ics and sub-harmonics, to name a few. The noise part can have a random and/or deterministic noise in both the amplitude and phase of the signal. Here we will look into the major sources of some of these un- wanted signals/noises. Oscillator noise performance is char- acterized as jitter in the time domain and as phase noise in the frequency domain. Which one is preferred, time or frequency domain, may depend on the application. In radio frequency (RF) communications, phase noise is preferred while in digital systems, jitter is favored. Hence, an RF engineer would prefer to address phase noise while a digital engineer wants jitter specified. Note that phase noise and jitter are two linked quantities associated with a noisy oscillator and, in general, as the phase noise increases in the oscillator, so does the jitter. The best way to illustrate this is to examine an ideal signal and corrupt it until the signal starts resembling the real output of an oscillator. The Perfect or Ideal Signal Figure 1 Figure 2 An ideal signal can be described math- ematically as follows: The new time and frequency domain representation is shown in Figure 2 while a vector representation of Equation 3 is illustrated in Figure 3 (a and b.) Equation 1 It turns out that oscillators are usually satu- rated in amplitude level and therefore we can Where: neglect the AM noise in Equation 3. -

Noise and Distortion Analysis of Dual Frequency Comb Photonic RF Channelizers
Research Article Vol. 28, No. 26 / 21 December 2020 / Optics Express 39750 Noise and distortion analysis of dual frequency comb photonic RF channelizers CALLUM DEAKIN1,2 AND ZHIXIN LIU1,3 1Department of Electronic and Electrical Engineering, University College London, London, UK [email protected] [email protected] Abstract: Dual frequency combs are emerging as highly effective channelizers for radio frequency (RF) signal processing, showing versatile capabilities in various applications including Fourier signal mapping, analog-to-digital conversion and sub-sampling of sparse wideband signals. Although previous research has considered the impact of comb power and harmonic distortions in individual systems, a rigorous and comprehensive performance analysis is lacking, particularly regarding the impact of phase noise. This is especially important considering that phase noise power increases quadratically with comb line number. In this paper, we develop a theoretical model of a dual frequency comb channelizer and evaluate the signal to noise ratio limits and design challenges when deploying such systems in a high bandwidth signal processing context. We show that the performance of these dual comb based signal processors is limited by the relative phase noise between the two optical frequency combs, which to our knowledge has not been considered in previous literature. Our simulations verify the theoretical model and examine the stochastic noise contributions and harmonic distortion, followed by a broader discussion of the performance limits of dual frequency comb channelizers, which demonstrate the importance of minimizing the relative phase noise between the two frequency combs to achieve high signal-to-noise ratio signal processing.