Joint Frequency-Setting and Pricing Optimization on Multi-Modal Transit Networks at Scale
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Japan by Rail for the COLOURS of AUTUMN
Japan by Rail for the COLOURS of AUTUMN HIGHLIGHTS of HONSHU 5 - 21 November 2019 with John Medcalf • TOKYO • SENDAI • NIIGATA • HAKONE • • KYOTO • HIROSHIMA • INUYAMA • OVERVIEW It’s not hard to argue the merits of train travel, but to truly HIGHLIGHTS discover how far rail technology has come in the last two centuries you simply have to visit Japan. Its excellent • Extensive rail travel using your JR Green Class (first class) Rail railway system is one of the world’s most extensive and Pass, including several journeys on the iconic bullet trains advanced, and train travel is unarguably the best way • Travel by steam train on the famous heritage railways of to explore this fascinating country. Speed, efficiency, Yamaguchi and the Banetsu lines comfort, convenience and a choice of spectacular destinations are hallmarks of travel by train in Japan. • Ride the Sagano Forest Railway, Tozan Mountain Railway, regional expresses, subways and a vintage tram charter in Tour summary Hiroshima • Cruise around the Matsushima Islands and Hiroshima Bay Join John Medcalf and discover the highlights of Japan’s main island Honshu on this exciting journey. to Miyajima It begins in the modern neon-lit capital of Tokyo, • Pay homage at Hiroshima Peace Park and visit the newly where the famous bullet train will take you north-west renovated museum to Niigata followed by a special steam train across • Explore historic temples, castles and cultural sites in Tokyo, the heart of Honshu. You’ll travel through mountains, Kyoto and Himeji valleys and forests full of deciduous trees ablaze with • Visit the unsurpassed modern railway museums in Tokyo autumn colours to Sendai where the story of Japan’s and Kyoto coast unfolds while exploring the Matsushima Islands. -

IEEE P1904.1 SIEPON Working Group Meeting Information for October2011 Kamakura, Japan
IEEE P1904.1 SIEPON Working Group Meeting Information for October2011 Kamakura, Japan 1. Meeting Dates October 11, 2011 (Tuesday) – October 13, 2011 (Thursday) 2. Meeting Location 2.1. Venue KAMAKURA PRINCE HOTEL 1-2-18 Shichirigahama - higashi, Kamakura, Kanagawa, 248-0025 Japan Tel: +81-(0)467-32-1111 Fax: +81-(0) 467-32-9290 http://www.princehotels.com/en/kamakura/ Meeting Room Kamakura Prince Hotel (Banquet Hall in the hotel) 2.2. Meeting Room Shichirigahama Banquet Hall 1 The spectacular view out to Enoshima and Mt. Fuji. Kamakura Prince Hotel Shichirigahama Banquet Hall, blessed by verdant and peaceful surroundings. 2.3. Location Hotel Location: http://www.princehotels.com/en/kamakura/access/ Tokyo Station Narita Airport Haneda Airport Kamakura Prince Hotel Yokohama Station Kamakura Station Local Area Map: http://www.princehotels.com/en/kamakura/access/ Kamakura Station The Great Buddha Tsurugaoka Hachiman Gu Shrine Kamakura Prince Hotel Shichirigahama Station 3. Transportation 3.1. From Narita Airport Train (JR) For details: http://www.narita-airport.jp/en/access/train/index.html From Narita International Airport, take the Narita Express train bound for Yokohama or Ofuna station. Narita Airport (JR Narita Express) → Yokohama (about 90 min) / Ofuna (about 105min) Yokohama (JR Yokosuka line) → Kamakura (about 24 min) Narita Express is a limited express train with all reserved seating. Both a fare ticket and a limited express ticket are required for boarding. Limousine bus For details: http://www.narita-airport.jp/en/access/bus/index.html From Narita International Airport take the Limousine bus to Yokohama station. Narita Airport → Yokohama Station (about 90min / 3,500 yen) Yokohama (JR Yokosuka line) → Kamakura (about 24 min / 330 yen) Yokohama (JR Tokaido or Yokosuka line) → Ofuna (about 15 min / 290 yen) At Kamakura station and Ofuna station, we recommend you should take a taxi to the Kamakura Prince Hotel. -

Faith and Power in Japanese Buddhist Art, 1600-2005
japanese art | religions graham FAITH AND POWER IN JAPANESE BUDDHIST ART, 1600–2005 Faith and Power in Japanese Buddhist Art explores the transformation of Buddhism from the premodern to the contemporary era in Japan and the central role its visual culture has played in this transformation. The chapters elucidate the thread of change over time in the practice of Bud- dhism as revealed in sites of devotion and in imagery representing the FAITH AND POWER religion’s most popular deities and religious practices. It also introduces the work of modern and contemporary artists who are not generally as- sociated with institutional Buddhism but whose faith inspires their art. IN JAPANESE BUDDHIST ART The author makes a persuasive argument that the neglect of these ma- terials by scholars results from erroneous presumptions about the aes- thetic superiority of early Japanese Buddhist artifacts and an asserted 160 0 – 20 05 decline in the institutional power of the religion after the sixteenth century. She demonstrates that recent works constitute a significant contribution to the history of Japanese art and architecture, providing evidence of Buddhism’s persistent and compelling presence at all levels of Japanese society. The book is divided into two chronological sections. The first explores Buddhism in an earlier period of Japanese art (1600–1868), emphasiz- ing the production of Buddhist temples and imagery within the larger political, social, and economic concerns of the time. The second section addresses Buddhism’s visual culture in modern Japan (1868–2005), specifically the relationship between Buddhist institutions prior to World War II and the increasingly militaristic national government that had initially persecuted them. -

Prudent Stable
Stable PrudentStable. Well positioned. Prudent. Well positioned Annual Report 2008 About Parkway Life REIT Parkway Life REIT is Asia’s largest listed healthcare REIT. It invests in income-producing real estate and real estate-related assets used primarily for healthcare and healthcare-related purposes. As at 31 December 2008, Parkway Life REIT’s total portfolio size stands at 13 properties totaling approximately S$1.05 billion. OUR MISSION We aim to deliver regular and stable distributions and achieve long term growth for our Unitholders. CONTENTS Our Reach 01 Financial Highlights 02 Significant Events 04 Message to Unitholders 08 Board of Directors 10 Management Team 12 Our Portfolio in Focus 16 Our Growth Strategy 36 Market Review and Outlook 40 Financial Review 43 Corporate Governance 45 Our Reach A MORE DIVERSIFIED PORTFOLIO In line with our aim of geographical and asset diversification, Parkway Life REIT (“PLife REIT”) significantly boosted its portfolio in 2008 with the completion of the acquisition of 10 healthcare properties in Japan. This brings our asset size to 13 properties from the initial portfolio of three hospital properties in Singapore, representing a 26% expansion in total portfolio size, from S$831.6 million in December 2007 to S$1.05 billion in December 2008. Leveraging on the strong growth of the Asia-Pacific healthcare industry, we will continue to source for opportunities to acquire high quality healthcare assets in the region to enhance our portfolio mix and yield-generating capability. PortFoLio Key StatiStiCS -
![Presentation [PDF/383KB]](https://docslib.b-cdn.net/cover/1229/presentation-pdf-383kb-1311229.webp)
Presentation [PDF/383KB]
FY2010.3 Second Quarter Financial Results Presentation October 29, 2009 East Japan Railway Company Contents I. FY2010.3 Second Quarter Financial Results (summary) II. JR East 2020 Vision - idomu - FY2010.3 Second Quarter Financial Results (summary) 4 Progress of JR East 2020 Vision (Transportation) 30 FY2010.3 Business Results Forecast 5 Progress of JR East 2020 Vision (Life-style Business) 31 Main Points of Business Results Forecast Revision 6 Progress of JR East 2020 Vision (Others) 32 Traffic Volume 7 Uses of Consolidated Cash Flows 33 Passenger Revenues 8 Numerical Targets 34 Passenger Revenues- Positive and Negative Factors 9 III. Reference Material Topics: Shinkansen Traffic Volume Segment Breakdown 36 and Passenger Revenues by Line 10 Development of ecute 37 Passenger Revenues - Progress toward Target 11 Hotel Operations - Overview 38 Topics: Second-Half Target for Passenger Revenues 12 Suica 39 Nonconsolidated Operating Expenses - Breakdown 13 Suica Electronic Money - Transactions and Compatible Stores 40 Nonconsolidated Operating Expenses - Main Positive Major Subsidiaries - Business Results 41 and Negative Factors 14 Breakdown of Operating Income 42 Nonconsolidated Financial Results 15 Key Financial Indicators 43 Transportation 16 Sales of Fixed Assets 44 Station Space Utilization 17 Breakdown of Long-term Debt 45 Shopping Centers & Office Buildings 18 Outlook of Debt Maturity 46 Tokyo Station City 19 Outlook of Bond Maturity 47 Other Services 20 Bond Issuances since FY2009.3 48 Summary of Non-Operating Income/Expenses and Total Long-term Debt - Credit Ratings 49 Extraordinary Gains/Losses (consolidated) 21 Cash Flows Summary (consolidated) 22 Consolidated Financial Results 23 Capital Expenditures (consolidated) 24 Nonconsolidated Capital Expenditures Plan 25 Total Long-term Debt (consolidated) 26 Forecast for FY2010.3 (consolidated) 27 * Items within dotted line are additional information for bond investors Forecast for FY2010.3 (nonconsolidated) 28 I. -

The Colours We Bring to Life Annual Report 2012 the Colours We Bring to Life
The COLOURS We Bring to Life annual report 2012 The COLOURS We Bring to Life In FY2012, ParkwayLife REIT (“PLife REIT”) continued to steadily enhance and grow its portfolio of healthcare properties in the region, catering to a broad spectrum of end users. Amidst the challenges of 2012, PLife REIT turned in a sterling performance and continued to give its best to all Unitholders. Driven by its strategies of proactive asset management, selective and strategic acquisitions, and dynamic financial management, PLife REIT remains steadfast in its commitment towards achieving long-term sustainable growth and stable distributions for its Unitholders. CONTENTS 02 Corporate Profile GreeninG Realising 03 Trust Structure our pastures 19 Portfolio in Focus Golden opportunities 51 Financial Review 25 Our Properties In the pink of health 53 Corporate Governance 05 Our Reach 67 Financial Contents 06 Financial Highlights Laying the 08 Significant Events yellow brick road 45 Our Growth Strategy Like well-polished silver 47 Investor Relations 10 Message to Unitholders 48 Market Review and Outlook 12 Board of Directors 16 Management Team ParkwayLife REIT Annual Report FY2012 CORPORATE PROFILE PLife REIT is one of Asia’s largest listed healthcare REITs. It invests in income-producing real estate and real estate-related assets used primarily for healthcare and healthcare-related purposes. As at 31 December 2012, PLife REIT’s total portfolio size stands at 37 properties totaling approximately S$1.4 billion. Mission Statement We aim to deliver regular and stable -

Area Locality Address Description Operator Aichi Aisai 10-1
Area Locality Address Description Operator Aichi Aisai 10-1,Kitaishikicho McDonald's Saya Ustore MobilepointBB Aichi Aisai 2283-60,Syobatachobensaiten McDonald's Syobata PIAGO MobilepointBB Aichi Ama 2-158,Nishiki,Kaniecho McDonald's Kanie MobilepointBB Aichi Ama 26-1,Nagamaki,Oharucho McDonald's Oharu MobilepointBB Aichi Anjo 1-18-2 Mikawaanjocho Tokaido Shinkansen Mikawa-Anjo Station NTT Communications Aichi Anjo 16-5 Fukamachi McDonald's FukamaPIAGO MobilepointBB Aichi Anjo 2-1-6 Mikawaanjohommachi Mikawa Anjo City Hotel NTT Communications Aichi Anjo 3-1-8 Sumiyoshicho McDonald's Anjiyoitoyokado MobilepointBB Aichi Anjo 3-5-22 Sumiyoshicho McDonald's Anjoandei MobilepointBB Aichi Anjo 36-2 Sakuraicho McDonald's Anjosakurai MobilepointBB Aichi Anjo 6-8 Hamatomicho McDonald's Anjokoronaworld MobilepointBB Aichi Anjo Yokoyamachiyohama Tekami62 McDonald's Anjo MobilepointBB Aichi Chiryu 128 Naka Nakamachi Chiryu Saintpia Hotel NTT Communications Aichi Chiryu 18-1,Nagashinochooyama McDonald's Chiryu Gyararie APITA MobilepointBB Aichi Chiryu Kamishigehara Higashi Hatsuchiyo 33-1 McDonald's 155Chiryu MobilepointBB Aichi Chita 1-1 Ichoden McDonald's Higashiura MobilepointBB Aichi Chita 1-1711 Shimizugaoka McDonald's Chitashimizugaoka MobilepointBB Aichi Chita 1-3 Aguiazaekimae McDonald's Agui MobilepointBB Aichi Chita 24-1 Tasaki McDonald's Taketoyo PIAGO MobilepointBB Aichi Chita 67?8,Ogawa,Higashiuracho McDonald's Higashiura JUSCO MobilepointBB Aichi Gamagoori 1-3,Kashimacho McDonald's Gamagoori CAINZ HOME MobilepointBB Aichi Gamagori 1-1,Yuihama,Takenoyacho -

Full Upgrade of ATOS to Improve Safety and Reliability of Railway Services
Hitachi Review Vol. 63 (2014), No. 8 493 Featured Articles Full Upgrade of ATOS to Improve Safety and Reliability of Railway Services Yasuhiro Yoshida OVERVIEW: Tokyo, Japan’s capital, has become one of the world’s major Kouhei Akutsu cities through the ongoing migration of people from the provinces as the Yasuhiro Yumita country’s economy has grown. The railways serving the Tokyo region are an important part of the social infrastructure that support the functioning of the Ryuji Yamagiwa city over a wide area. Their ongoing development has created a complex and Hideki Osumi high-density network, including the Chuo and Shonan-Shinjuku Lines, among Mitsunori Okada others. Future railway systems are expected to satisfy new requirements Kiyosumi Fukui arising from the changing social environment, including the utilization of existing infrastructure to allow different operators to run services on the same track, and further improvements to passenger services. To achieve this, JR-East and Hitachi aim to provide safe and reliable management of railway traffic, and to help improve services to all stakeholders, including passengers, through initiatives such as the fusion of control and information technologies. has facilitated ongoing work to add new lines to the INTRODUCTION system without affecting those lines where it was WHEN the East Japan Railway Company (JR- already operating. With the system now covering East) was established in 1987, very little progress 20 lines, amounting to a combined length of about had yet been made on the computerization of train 1,270 km, it has become an important part of the social traffic management on its metropolitan lines in infrastructure, essential to the ongoing provision of the Tokyo region, with traffic management for safe and reliable transportation (see Fig. -
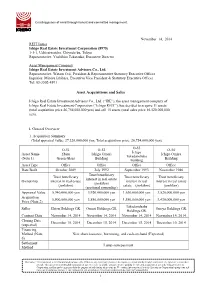
Acquisition Release (11/14/2014)
Creating peace of mind through honest and committed management. November 14, 2014 REIT Issuer Ichigo Real Estate Investment Corporation (8975) 1-1-1, Uchisaiwaicho, Chiyoda-ku, Tokyo Representative: Yoshihiro Takatsuka, Executive Director Asset Management Company Ichigo Real Estate Investment Advisors Co., Ltd. Representative: Wataru Orii, President & Representative Statutory Executive Officer Inquiries: Minoru Ishihara, Executive Vice President & Statutory Executive Officer Tel: 03-3502-4891 Asset Acquisitions and Sales Ichigo Real Estate Investment Advisors Co., Ltd. (“IRE”), the asset management company of Ichigo Real Estate Investment Corporation (“Ichigo REIT”), has decided to acquire 11 assets (total acquisition price 26,754,600,000 yen) and sell 15 assets (total sales price 16,520,000,000 yen). I. General Overview 1. Acquisition Summary (Total appraisal value: 27,220,000,000 yen, Total acquisition price: 26,754,600,000 yen) O-53 O-51 O-52 O-54 Ichigo Asset Name Ebisu Ichigo Omori Ichigo Omiya Takadanobaba (Note 1) Green Glass Building Building Building Asset Type Office Office Office Office Date Built October 2009 July 1992 September 1993 November 1986 Trust beneficiary Trust beneficiary Trust beneficiary Trust beneficiary interest in real estate Ownership interest in real estate interest in real interest in real estate (juekiken) (juekiken) estate (juekiken) (juekiken) (sectional ownership) Appraisal Value 5,940,000,000 yen 3,920,000,000 yen 1,630,000,000 yen 3,520,000,000 yen Acquisition 5,900,000,000 yen 3,850,000,000 yen 1,580,000,000 yen 3,430,000,000 yen Price (Note 2) Takadanobaba Seller Ebisu Holdings GK Omori Holdings GK Omiya Holdings GK Holdings GK Contract Date November 14, 2014 November 14, 2014 November 14, 2014 November 14, 2014 Closing Date December 10, 2014 December 15, 2014 December 15, 2014 December 10, 2014 (expected) Financing Method (Note New share issuance, borrowing, and cash-on-hand (Expected) 6) Settlement Lump-sum payment Method Disclaimer: This translation is for informational purpose only. -

Japan Rail Pass
cross Japan with discount Travel a passes A large store with a rooftop garden, Kanagawa Several convenient and budget-friendly travel passes are available to aid perfect for families! Kanagawa travelers exploring multiple regions of Japan. Be sure to stop by at Ito-Yokado Ito-Yokado Grand Tree Musashi Kosugi and Ario at each destination for all your gift and shopping needs! 武蔵小杉 3-1135-1 Shinmarukohigashi, Nakahara-ku, Kawasaki-shi, Kanagawa 10:00-21:00 / 1F restaurants 11:00-23:00 / 1F cafes 10:00-22:00 Hokkaido Hokkaido Aomori Osaka Shinjuku → JR Shonan Shinjuku Line: Musashi-Kosugi Sta. approx. 21min. by rail → Musashi-Kosugi JR Nambu Line 2 Front Exit2 Japan Rail Pass Kanagawa In front of Musashi-Kosugi Station! Across Japan Ito-Yokado C Nagano Area This discount pass is perfect for people who want to travel across Japan Musashi Ito-Yokado Musashi Kosugi Ekimae Stores you can visit using this pass from Hokkaido to Kyushu. It offers unlimited rides on all JR lines across the Kosugi 3-420 Kosugimachi, Nakahara-ku, Kawasaki-shi, Kanagawa ●Ueda (Ueda Station) nation! Enjoy shopping at any of the following Ito-Yokado and Ario locations Musashi-Kosugi Sta. A JR Yokosuka Line Hokkaido Area ●Nagano (Nagano Station) in Japan using this pass: Musashi-Kosugi Sta. B1F・1F 9:00-22:00 / 2-5F 9:00-21:00 ●Sapporo (Sapporo Station) ●Minami Matsumoto (Minami-Matsumoto Station) Shinjuku → JR Shonan Shinjuku Line: New South Gate approx. 21min. by rail → Musashi-Kosugi ●Susukino (Susukino Station) ●Asahikawa (Asahikawa Station) D E Kanto Area ●Omori (Omori -

IEEE P1904.1 SIEPON Working Group Meeting Information for October2011 Kamakura, Japan
IEEE P1904.1 SIEPON Working Group Meeting Information for October2011 Kamakura, Japan 1. Meeting Dates October 11, 2011 (Tuesday) – October 13, 2011 (Thursday) 2. Meeting Location 2.1. Venue KAMAKURA PRINCE HOTEL 1-2-18 Shichirigahama - higashi, Kamakura, Kanagawa, 248-0025 Japan Tel: +81-(0)467-32-1111 Fax: +81-(0) 467-32-9290 http://www.princehotels.com/en/kamakura/ Meeting Room Kamakura Prince Hotel (Banquet Hall in the hotel) 2.2. Meeting Room Shichirigahama Banquet Hall 1 The spectacular view out to Enoshima and Mt. Fuji. Kamakura Prince Hotel Shichirigahama Banquet Hall, blessed by verdant and peaceful surroundings. 2.3. Location Hotel Location: http://www.princehotels.com/en/kamakura/access/ Tokyo Station Narita Airport Haneda Airport Kamakura PPPrincePrince Hotel Yokohama Station Kamakura Station Local Area Map: http://www.princehotels.com/en/kamakura/access/ Kamakura Station The Great Buddha Tsurugaoka Hachiman Gu Shrine Kamakura Prince Hotel ShichiriShichirigahamagahama Station 3. Transportation 3.1. From Narita Airport Train (JR) For details: http://www.narita-airport.jp/en/access/train/index.html From Narita International Airport, take the Narita Express train bound for Yokohama or Ofuna station . Narita Airport (JR Narita Express) → Yokohama (about 90 min) / Ofuna (about 105min) Yokohama (JR Yokosuka line) → Kamakura (about 24 min) Narita Express is a limited express train with all reserved seating. Both a fare ticket and a limited express ticket are required for boarding. Limousine bus For details: http://www.narita-airport.jp/en/access/bus/index.html From Narita International Airport take the Limousine bus to Yokohama station. Narita Airport → Yokohama Station (about 90min / 3,500 yen) Yokohama (JR Yokosuka line) → Kamakura (about 24 min / 330 yen) Yokohama (JR Tokaido or Yokosuka line) → Ofuna (about 15 min / 290 yen) At Kamakura station and Ofuna station , we recommend you should take a taxi to the Kamakura Prince Hotel. -

Ito-Yokado’S Basic Approach to Business
Japan Expert Shopping Guide This image illustrates Ito-Yokado’s basic approach to business. We started as a small sapling and grew into a large tree over 100 We aim to be a sincere We aim to be a sincere We aim to be a sincere In 2020, Ito-Yokado years. The doves on the tree’s branches represent all the company that company that our business company that stakeholders of our company—customers, business partners, our customers trust. partners, shareholders and our employees trust. and employees—who are gathered peacefully and keep our local communities trust. business going. will anniversary celebrate th as its 100 Products from the 1980’s Japan’s largest supers Did you one of tores know? 100 th Anniversary 2020 1st logo The history of 1958 -1964 Ito-Yokado opens our logo in a multi-story building occupying With your support, we celebrate the basement floor to the 6th floor. The Ito-Yokado logo design It stocks everything from features a dove, a symbol our 100th anniversary! 2nd logo 1964 -1972 everyday household items to of peace. It has been used clothes and groceries. since 1958. 2007 In the current logo, blue 1967 means a clear sky (future), Current logo 1972 onward We begin selling products under our original red means passion, and The company brand is born. “Seven Premium” brand white means sincerity. Originally a clothing store, 2011 we started with apparel Starting with only before expanding our lineup to food 49 items, Seven Premium 2013 and basic necessities. has since expanded to over 4,000 items including food, 2015 Surprisingly, there’s The first store in Kitasenju was small, with This laid the foundation for still a store in this only 6.6 square meters of retail space.