Tidal Variability in the Hong Kong Region
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

List of Recognized Villages Under the New Territories Small House Policy
LIST OF RECOGNIZED VILLAGES UNDER THE NEW TERRITORIES SMALL HOUSE POLICY Islands North Sai Kung Sha Tin Tuen Mun Tai Po Tsuen Wan Kwai Tsing Yuen Long Village Improvement Section Lands Department September 2009 Edition 1 RECOGNIZED VILLAGES IN ISLANDS DISTRICT Village Name District 1 KO LONG LAMMA NORTH 2 LO TIK WAN LAMMA NORTH 3 PAK KOK KAU TSUEN LAMMA NORTH 4 PAK KOK SAN TSUEN LAMMA NORTH 5 SHA PO LAMMA NORTH 6 TAI PENG LAMMA NORTH 7 TAI WAN KAU TSUEN LAMMA NORTH 8 TAI WAN SAN TSUEN LAMMA NORTH 9 TAI YUEN LAMMA NORTH 10 WANG LONG LAMMA NORTH 11 YUNG SHUE LONG LAMMA NORTH 12 YUNG SHUE WAN LAMMA NORTH 13 LO SO SHING LAMMA SOUTH 14 LUK CHAU LAMMA SOUTH 15 MO TAT LAMMA SOUTH 16 MO TAT WAN LAMMA SOUTH 17 PO TOI LAMMA SOUTH 18 SOK KWU WAN LAMMA SOUTH 19 TUNG O LAMMA SOUTH 20 YUNG SHUE HA LAMMA SOUTH 21 CHUNG HAU MUI WO 2 22 LUK TEI TONG MUI WO 23 MAN KOK TSUI MUI WO 24 MANG TONG MUI WO 25 MUI WO KAU TSUEN MUI WO 26 NGAU KWU LONG MUI WO 27 PAK MONG MUI WO 28 PAK NGAN HEUNG MUI WO 29 TAI HO MUI WO 30 TAI TEI TONG MUI WO 31 TUNG WAN TAU MUI WO 32 WONG FUNG TIN MUI WO 33 CHEUNG SHA LOWER VILLAGE SOUTH LANTAU 34 CHEUNG SHA UPPER VILLAGE SOUTH LANTAU 35 HAM TIN SOUTH LANTAU 36 LO UK SOUTH LANTAU 37 MONG TUNG WAN SOUTH LANTAU 38 PUI O KAU TSUEN (LO WAI) SOUTH LANTAU 39 PUI O SAN TSUEN (SAN WAI) SOUTH LANTAU 40 SHAN SHEK WAN SOUTH LANTAU 41 SHAP LONG SOUTH LANTAU 42 SHUI HAU SOUTH LANTAU 43 SIU A CHAU SOUTH LANTAU 44 TAI A CHAU SOUTH LANTAU 3 45 TAI LONG SOUTH LANTAU 46 TONG FUK SOUTH LANTAU 47 FAN LAU TAI O 48 KEUNG SHAN, LOWER TAI O 49 KEUNG SHAN, -

GEO REPORT No. 282
EXPERT REPORT ON THE GEOLOGY OF THE PROPOSED GEOPARK IN HONG KONG GEO REPORT No. 282 R.J. Sewell & D.L.K. Tang GEOTECHNICAL ENGINEERING OFFICE CIVIL ENGINEERING AND DEVELOPMENT DEPARTMENT THE GOVERNMENT OF THE HONG KONG SPECIAL ADMINISTRATIVE REGION EXPERT REPORT ON THE GEOLOGY OF THE PROPOSED GEOPARK IN HONG KONG GEO REPORT No. 282 R.J. Sewell & D.L.K. Tang This report was originally produced in June 2009 as GEO Geological Report No. GR 2/2009 2 © The Government of the Hong Kong Special Administrative Region First published, July 2013 Prepared by: Geotechnical Engineering Office, Civil Engineering and Development Department, Civil Engineering and Development Building, 101 Princess Margaret Road, Homantin, Kowloon, Hong Kong. - 3 - PREFACE In keeping with our policy of releasing information which may be of general interest to the geotechnical profession and the public, we make available selected internal reports in a series of publications termed the GEO Report series. The GEO Reports can be downloaded from the website of the Civil Engineering and Development Department (http://www.cedd.gov.hk) on the Internet. Printed copies are also available for some GEO Reports. For printed copies, a charge is made to cover the cost of printing. The Geotechnical Engineering Office also produces documents specifically for publication in print. These include guidance documents and results of comprehensive reviews. They can also be downloaded from the above website. The publications and the printed GEO Reports may be obtained from the Government’s Information Services Department. Information on how to purchase these documents is given on the second last page of this report. -

Recommended District Council Constituency Areas
District : Tai Po Recommended District Council Constituency Areas +/- % of Population Estimated Quota Code Recommended Name Boundary Description Major Estates/Areas Population (17,282) P01 Tai Po Hui 15,006 -13.17 N Lam Tsuen River, Po Heung Bridge Po Heung Street, Plover Cove Road NE Plover Cove Road E Tai Po River, Nam Wan Road SE Nam Wan Road, MTR (East Rail Line) S MTR (East Rail Line) SW MTR (East Rail Line) W MTR (East Rail Line) NW MTR (East Rail Line), Lam Tsuen River P02 Tai Po Central 14,196 -17.86 N On Po Road 1. TAI PO CENTRE 2. TAI PO PLAZA NE On Po Road, Nam Wan Road E Nam Wan Road SE Nam Wan Road, Lam Tsuen River S Lam Tsuen River SW Lam Tsuen River, Po Wu Lane W On Chee Road NW P1 District : Tai Po Recommended District Council Constituency Areas +/- % of Population Estimated Quota Code Recommended Name Boundary Description Major Estates/Areas Population (17,282) P03 Chung Ting 15,335 -11.27 N Ting Lai Road, Chung Nga Road 1. CHUNG NGA COURT 2. EIGHTLAND GARDENS NE Chung Nga Road 3. FORTUNE PLAZA E Ting Kok Road, On Cheung Road 4. FU HENG ESTATE (PART) : Heng Tai House SE Lam Tsuen River 5. JADE PLAZA S Lam Tsuen River 6. TING NGA COURT 7. TREASURE GARDEN SW Lam Tsuen River, Ting Kok Road W Ting Kok Road NW Ting Kok Road, Ting Lai Road P04 Tai Yuen 14,808 -14.32 N Ting Kok Road 1. TAI YUEN ESTATE NE Ting Kok Road, Nam Wan Road E Nam Wan Road SE Nam Wan Road, On Po Road S On Po Road, On Tai Road SW On Cheung Road W Ting Kok Road NW Ting Kok Road P2 District : Tai Po Recommended District Council Constituency Areas +/- % of Population Estimated Quota Code Recommended Name Boundary Description Major Estates/Areas Population (17,282) P05 Fu Heng 16,532 -4.34 N Chung Nga Road, Chuen On Road 1. -

International Society for Soil Mechanics and Geotechnical Engineering
INTERNATIONAL SOCIETY FOR SOIL MECHANICS AND GEOTECHNICAL ENGINEERING This paper was downloaded from the Online Library of the International Society for Soil Mechanics and Geotechnical Engineering (ISSMGE). The library is available here: https://www.issmge.org/publications/online-library This is an open-access database that archives thousands of papers published under the Auspices of the ISSMGE and maintained by the Innovation and Development Committee of ISSMGE. Wettability of natural surface soils of Hong Kong B.H.W. Li, T.H.Y. Lam & S.D.N. Lourenço Department of Civil Engineering, The University of Hong Kong, Hong Kong S.A.R. ABSTRACT: Changes in soil wettability impact the hydraulic and mechanical behavior of soils. The occur- rence and consequences of soil water repellency have been reported in many parts of the world and mostly within an agricultural and hydrologic context, but little is known on its existence in regions with a sub- tropical climate (such as Hong Kong) and within a geotechnical context. The aim of this paper is to conduct a preliminary investigation on the wettability of natural soils from Hong Kong. At 120 locations across the ter- ritory, samples of soil overlying different geological materials were collected from the surface layer (0-5cm). The persistence of soil water repellency was determined by using the Water Drop Penetration Time (WDPT) test on field-moist samples. The degree of soil water repellency was determined via contact angle measure- ments (CA) using the Sessile Drop Method (SDM). Based on the results, the prevailing underlying geological materials dictate the persistence and degree of the soil water repellency. -

TOLO HARBOUR 史提福樓 Trackside Villas Strafford House 員工會所港鐵 峰林軒 Daisyfield
TAI PO ROAD - TAI PO KAU 東頭灣徑 策誠軒 I TOLO HARBOUR 史提福樓 Trackside Villas Strafford House 員工會所港鐵 峰林軒 Daisyfield 9 大 埔 滘 8 燕 子 里 Y 7 2 IN 叠翠豪庭 農瑞村 TSE LANE 10 1 9 吐 露 港 公 路 TAI PO KAU! Emerald 海景山莊 20 Palace 20 Seaview Villas 2 1 南苑 Southview Villas YAT YIU AVE 皇御山 The Kingston Hills 4A 逸遙路 松 苑 Tolo Ridge H U 大埔滘老圍 逍遙雋岸 N G L'Utopie L A 白鷺湖 Tai Po Kau M 互動中心 D Lo Wai 41 1 1 50 42 40 R 55 I Lake Egret V 43 E Nature Park 8 3 紅 林 路 35 60 35 44 ! 6 紅 林 居 翡翠花園 滌濤山 65 45 30 The Mangrove 8 Savanna Garden14 Constellation 大埔滘新圍 T 46 KOU LIN O K 10 Cove O 24 L 12 47 25 ! Tai Po Kau 1 19 大 埔 公 路 ─ 大 埔 滘 段 15 San Wai 蔚海山莊 8 48 20 1 10 20 5 Villa Costa 49 23 11 12 15 10 6 15 16 天賦海灣 7 10 白石角配水庫 3 荔枝坑 瞭望里 Pak Shek Kok Providence Bay 1 Ser Res 9 Lai Chi Hang 大埔滘 優 景 里 18 公園 3 墨爾文 20 21 40 19 新翠山莊 8 鹿茵山莊 Malvern 38 ! 10 FO CHUN ROAD Villa Castell 7 DeerHill Bay 7 6 海鑽 18 大 36 16 科 進 路 天賦海灣 32 24 1 10 11 溋玥 1 埔 The Graces 創新 路 9 天賦海灣 公 9 5 8 松仔園 路 22 Providence Peak ! 8 ─ 26 6 5 7 Tsung Tsai Yuen 大 YAU KING LANE 9 3 埔 II 10 逸瓏灣 100 滘 1 1 白石角海濱長廊 段 科城路 街坊婦女會 3 Mayfair by the Sea 15 L I Japanese 孫方中 5 12 3 A 泵房 1 FO CHUN ROAD R Int'l School I T 保良局 香港教育大學 1 碼頭 18 7 16 21 田家炳千禧 運動中心 E FO SHING RD 18 R 博研路 8 18 U The Education 雲滙 T 21 University 3 11 10 16 A 12 H1 A1 N of Hong Kong St Martin A2 U Sports Centre 10 7 海日灣 A 6 H9 段 K 6 鉛 O D1 The Horizon P 8 滘 I 200 嘉熙 D2 ─ A 蕉坑 道 T 5 B2 大埔滘 埔 滘 林 T 5 8 Solaria C1 Pak Shek Kok Promenade 管理站 大 A 徑 I Tsiu Hang 優 景 里 ! 3 C2 育 P East Rail Line 10 教 O 自然 CHONG SAN ROAD 埔滘 R 3 TOLO HIGHWAY1 大 O 碗窰 Wun Yiu Yiu Wun 碗窰 A -

Introduction
INTRODUCTION 1) Background In many people’s minds, Hong Kong is the “Pearl of the Orient” and a compact cosmopolitan city of skyscrapers and shopping arcades. Whether it is the foreign tourists or the locals, they always envision activities like shopping and sightseeing as the tourists’ ultimate activities. Renowned landmarks like the Peak and Tsing Ma Bridge are seen as the must-goes and final stops on their itineraries. However, few seem to realize the city has its peculiar and exotic side. With its rich cultural diversity, more than 260 outlying islands, 100 walking trails, 4 marine parks, Hong Kong promises wonderful landscapes, dramatic and stunning rock formations, craggy mountains, quaint villages, inviting flora and fauna, abundant cultural heritage which cater for not only the interests of the shoppers but also the most adventurous explorers. It is well worth the efforts to explore these charming rural retreats in Hong Kong. The aim of this project is to examine these adventurous places in Hong Kong. As there are many hotels tourists can choose from in Tsim Sha Tsui, we will start our exploration of these adventurous places from there. 1 B) Definitions and our understanding of Adventure Tourism Definitions According to the information given by Queensland Tourism Board, adventure tourism can be classified into two main categories, namely i) Hard adventure tourism ii) Soft adventure tourism There is a distinction between the two kinds of adventure tourism. For hard adventure tourism, it combines a unique experience in an outdoor setting with excitement and a degree of risk. It frequently demands physical exertion as well as a level of skill. -

District : Tai Po
District : Tai Po Proposed District Council Constituency Areas +/- % of Population Projected Quota Code Proposed Name Boundary Description Major Estates/Areas Population (16 599) P01 Tai Po Hui 19 451 +17.18 N Plover Cove Road, Po Heung Bridge 1. JADE GARDEN 2. MOUNTAIN VIEW COURT Po Heung Street 3. PO HEUNG ESTATE NE Plover Cove Road E Nam Wan Road, Tai Po River Tai Po Road - Yuen Chau Tsai SE MTR(East Rail Line), Nam Wan Road S MTR(East Rail Line) SW MTR(East Rail Line) W MTR(East Rail Line) NW Lam Tsuen River, MTR(East Rail Line) Pak Shing Street P02 Chung Ting 14 303 -13.83 N Ting Lai Road 1. CHUNG NGA COURT 2. EIGHTLAND GARDENS NE Chung Nga Road 3. FORTUNE PLAZA E On Cheung Road, Ting Kok Road 4. FU HENG ESTATE (PART) : Heng Tai House SE Lam Tsuen River, On Chee Road, On Po Road 5. JADE PLAZA S Lam Tsuen River 6. TING NGA COURT 7. TREASURE GARDEN SW Lam Tsuen River, Ting Kok Road W Ting Kok Road NW Ting Lai Road P 1 District : Tai Po Proposed District Council Constituency Areas +/- % of Population Projected Quota Code Proposed Name Boundary Description Major Estates/Areas Population (16 599) P03 Tai Po Central 13 645 -17.80 N On Po Road, On Tai Road 1. TAI PO CENTRE 2. TAI PO PLAZA NE Nam Wan Road, On Po Road E Nam Wan Road SE Lam Tsuen River, Nam Wan Road S Lam Tsuen River SW Lam Tsuen River, Po Wu Lane Tai Po Tai Wo Road W On Chee Road, On Po Road, On Pong Road NW P04 Tai Yuen 13 863 -16.48 N Ting Kok Road 1. -

Planning Department M/Ne/09/78
Tai Lung Crematorium 200 Wa Mei Shan Lo Wai Sha Lo Tung Cheung Uk Kiu Tau 336 ³¶ E¯ 300 Ma Tseuk Ø¿⁄ Gallant F¨¹Ã} Tong Water Tunnel Garden 100 û¤ Sha Lo Tung s¤ 200 NGAU AU E⁄s| Lei Uk Shan Liu E⁄s SHA LO TUNG C 100 Kau Lung Hang eªw C San Wai CLOUDY HILL ¸¤ ( KAU LUNG HANG SHAN ) Ho Lek Pui C n« Yuen Leng 100 M'Xƒ p†s 100 Nam Wa Po 440 Lai Pek Shan 205 400 j⁄ Wo Hop Shek Cemetery San Tsuen Tai Mei Tuk 200 300 82 d§Î C «¤ ªÄO Ng Uk Tsuen ¶¸ Wong Chuk Tseng Tau Å¥ Lo Tsz Tin s Ø¿⁄ Ting Kok Tsuen 200 ~ C }¬ Lung Mei A Shan ¼¿ Tung Tsz ‹¥ 300 j¤ 282 Po Sam Pai Tsiu Lam Å¥¤ Tai Wo 200 t A` 100 200 Ser Res Lookout Water Tunnel ˘Y TING ¤fl San Tau Kok KOK ROAD 46 Water Tunnel Tsz Tong õ® ‡ A` Wai Ha 400 Lookout Tsuen Tai Hang Ø¿⁄ 400 »›·—– A` Hong Kong Institute 300 Lookout A` of Education SHUEN WAN Lookout 480 ñ»é¶ t 288 400 _¥j¤ Fung Yuen Ser Res Lo Tsuen t ˚›s PAK TAI TO YAN Ser Res Forest Hill WAI TAU TSUEN ¼½a Ha Tei Ha 506 CHE TEI Á³ †W˘ Mak Uk L²ë Shuen Wan Casa Marina Chim Uk Qª y¬ U¤ ¯„´ ¶‰ †W˘ ‡Y Pinehill Lau Hang Ha Hang Wong Yue Tan Shuen Wan Wai Tau Tsuen Å¥¤ Richwood Park Lei Uk d– Village E»¨» K¯ Tycoon Place Hong Lok Yuen FUNG YUEN †W˘ v¬ Tit Mei Tsai TAI 100 j¤H® Shuen Wan 44 û¤º Tai Po D YEUNG CHAU ¥ ¯ªË Ð¥ A Chan Uk ª¯Â Hospital O Ngau Kwu Leng Wo Tong Pui PO Tin Sam Cho Ma Wu Kau Shi Wai R K Ø¿⁄ O ¤¸«w‹S û¸d R K t¤I ' O n« G F¨ Kau Liu Ha Pumping AD IN Chuen Pei Nam Hang I´ë T Sha Lan Station Water Tunnel ˦ ”¤·¥ æ⁄Q§ Lung |§U Fu Heng ®¶º´ 468 fi 110 Chuk Hang Nethersole Fortune Garden The Beverly Hills 400 ½³ Hang Ha Po -

Annotated Checklist of Hongkong Lichens
57 Tropical Bryology 17: 57-101, 1999 Annotated checklist of Hongkong Lichens André Aptroot Centraalbureau voor Schimmelcultures, P.O. Box 273, NL-3740 AG Baarn, The Netherlands Mark R.D. Seaward Department of Environmental Science, University of Bradford, Bradford, West Yorkshire BD7 1DP, United Kingdom Abstract. An annotated checklist of the lichens of Hong Kong, based on all available literature reports and specimens, including those recently collected by the authors, is presented. In total, 261 species are reported, of which 176 are new records for Hong Kong, 132 of which are new for China, 43 are new for East Asia, and 27 are new for Asia. The lichen vegetation is mainly tropical, as is shown by the distribution patterns of the identified species: 53 species are cosmopolitan, 40 northern temperate, 122 pantropical, 17 paleotropical and 29 endemic to tropical East Asia. With regard to substrata, 129 species are corticolous, 148 saxicolous, 17 foliicolous and 19 terricolous. Four species are newly described: Anisomeridium conorostratum Aptroot, A. hydei Aptroot, Caloplaca pulicarioides Aptroot and Placidiopsis poronioides Aptroot. The flora is rather poor in species; for example, no Caliciales have been found. In the past, the numbers of species of several groups such as the Graphidaceae, Heterodermia and Xanthoparmelia have been overestimated, whereas few pyrenocarps have been reported. The flora of wet granitic outcrops is surprisingly well developed in Hong Kong. Although not a single Peltula species was reported before, six species were identified, including one that was previously only known from Africa. In addition, several other cyanophilic genera are present, such as Euopsis, Psorotichia, Pyrenopsis and, most unexpectedly, Vestergrenopsis, each with one species. -

Country Park Enclaves Already Covered by Outline Zoning Plan
CB(1) 2721/09-10(01) Annex Country Park Enclaves already covered by Outline Zoning Plan Area in ha No. Name of site (About) Lion Rock Country Park 1 Shap Yi Wat 3 Ma On Shan Country Park 2 Ngau Liu and Kwun Yam Shan 72 3 Wong Chuk Yeung 37 Pat Sin Leng Country Park 4 Sha Lo Tung 56 Plover Cove Country Park 5 Kai Kuk Shue Ha, Ho Lek Pui and Ham Hang Mei 8 6 Ho Pui, Tin Sam, Sam Ka Tsuen, San Uk Tsuen, San 98 Uk Ha, Lo Wai, Leng Pui and Kau Tam Tso Sai Kung East and West Country Parks 7 Wong Yi Chau and Hei Tsz Wan 9 8 Pak Tam Chung 2 9 Tsak Yue Wu 15 10 Tai Long, Lam Uk Wai, Lung Mei Tau, Tai Wan and 46 Ham Tin 11 Pak Tam 5 12 Shek Hang 3 13 Tai Mong Tsai, She Tau, Ping Tun, Tit Kim Hang, Tam Wat, Tai Po Tsai, San Tin Hang, Tso Wo Hang, Wong 126 Chuk Wan and Wong Mo Ying 14 Wong Keng Tei and Tsam Chuk Wan 36 15 Sham Chung 32 Lantau South, North and North (Extension) Country Parks 16 Fan Lau Tsuen 24 17 Pak Fu Tin 3 18 Lung Mei and Tai Long 28 19 Ngong Ping 103 20 Lai Chi Yuen 5 21 Shui Tseng Wan 2 22 Yi Long 7 23 Shui Hau Wan 1 1 Annex Country Park Enclaves not covered by Outline Zoning Plans Area in ha No. Name of site (About) Ma On Shan Country Park 24 Mau Ping, Mau Ping Lo Uk, Mau Ping San Uk, and 45 Wong Chuk Shan Kam Shan Country Park 25 Kam Shan 1 Tai Mo Shan Country Park 26 Site near Chuen Lung 10 27 Site near Tso Kung Tam 9 Tai Lam Country Park 28 Tin Fu Tsai 53 29 Tsing Fai Tong 26 30 Sheung Tong 10 31 Sheung Fa Shan 26 32 Yuen Tun 19 Pat Sin Leng Country Park 33 Ping Shan Chai 15 Plover Cove Country Park 34 Hung Shek Mun Tsuen -
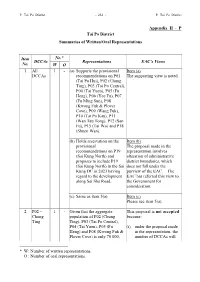
Appendix II - P Tai Po District Summaries of Written/Oral Representations
P. Tai Po District - 252 - P. Tai Po District Appendix II - P Tai Po District Summaries of Written/Oral Representations Item No.* DCCAs Representations EAC’s Views No. W O 1 All 1 - (a) Supports the provisional Item (a) DCCAs recommendations on P01 The supporting view is noted. (Tai Po Hui), P02 (Chung Ting), P03 (Tai Po Central), P04 (Tai Yuen), P05 (Fu Heng), P06 (Yee Fu), P07 (Fu Ming Sun), P08 (Kwong Fuk & Plover Cove), P09 (Wang Fuk), P10 (Tai Po Kau), P11 (Wan Tau Tong), P12 (San Fu), P15 (Tai Wo) and P18 (Shuen Wan). (b) Holds reservation on the Item (b) provisional The proposal made in the recommendations on P19 representation involves (Sai Kung North) and alteration of administrative proposes to include P19 district boundaries, which (Sai Kung North) in the Sai does not fall under the Kung DC in 2023 having purview of the EAC. The regard to the development EAC has referred this view to along Sai Sha Road. the Government for consideration. (c) Same as item 5(a). Item (c) Please see item 5(a). 2 P02 – 1 - Given that the aggregate This proposal is not accepted Chung population of P02 (Chung because: Ting Ting), P03 (Tai Po Central), P04 (Tai Yuen), P05 (Fu (i) under the proposal made Heng) and P08 (Kwong Fuk & in the representation, the Plover Cove) is only 70 000, number of DCCAs will * W: Number of written representations. O : Number of oral representations. P. Tai Po District - 253 - P. Tai Po District Item No.* DCCAs Representations EAC’s Views No. -
App B Text 2
Appendix B Wave and Sediment Modelling Report (September 2007) [Appendices not included] Halcrow China Limited AGREEMENT NO. CE 59/2005 (EP) Development of a Bathing Beach at Lung Mei, Tai Po Environmental, Drainage and Traffic Impact Assessments - Investigation Working Paper 2.5 - Wave and Sediment Modelling Report September 2007 The Government of Hong Kong Special Administrative Region Civil Engineering and Development Department Port Works Division Agreement No. CE 59/2005 (EP) Development of a Bathing Beach at Lung Mei, Tai Po Environmental, Drainage and Traffic Impact Assessments - Investigation CONTENTS 1. INTRODUCTION 1 1.1 General .............................................................................................................. 1 1.2 Brief Description of Project............................................................................... 1 1.3 Objectives .......................................................................................................... 1 1.4 Structure of this report....................................................................................... 2 2. WAVE MODELLING 3 2.1 Wave Hindcasting ............................................................................................. 3 2.2 Extreme Wave Conditions ................................................................................. 7 3. CROSS-SHORE MODELLING 10 3.1 Background...................................................................................................... 10 3.2 Description of COSMOS................................................................................