DOCSLIB.ORG

THERMODYNAMICS Entropy: Entropy Is Defined As a Quantitative Measure of Disorder Or Randomness in a System. the Heat Change, Dq

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
THERMODYNAMICS Entropy: Entropy Is Defined As a Quantitative Measure of Disorder Or Randomness in a System. the Heat Change, Dq Produced with a Trial Version of PDF Annotator - www.PDFAnnotator.com THERMODYNAMICS Entropy: Entropy is defined as a quantitative measure of disorder or randomness in a system. The heat change, dq and the temperature T are thermodynamic quantities. A thermodynamic function whose change (dq/T) is independent of the path of the system is called entropy 푑푆 = 푑푞 푇 1. Entropy is a state function whose magnitude depends only on the parameters of the system and can be expressed in terms of (P,V,T) 2. dS is a perfect differential. Its value depends only on the initial and final states of the system 3. Absorption of heat increases entropy of the system. In a reversible adiabatic change dq=0, the entropy change is zero 4. For carnot cycle ∮ 푑푆 = 0 5. The net entropy change in a reversible process is zero, ∆푆푢푛푖푣푒푟푠푒 = ∆푆푠푦푠푡푒푚 + ∆푆푠푢푟푟표푢푛푑푖푛푔 = 0 In irreversible expansion ∆푆푢푛푖푣 = +푣푒 cyclic processs, ∆푆푢푛푖푣 > 0 All natural process will take place in a direction in which the entropy would increase. A thermodynamically irreversible process is always accompanied by an increase in the entropy of the system and its surroundings taken together while in a thermodynamically reversible process, the entropy of the system and its surroundings taken together remains constant. Entropy change in isothermal and reversible expansion of ideal gas: In isothermal expansion of an ideal gas carried out reversibly, there will be no change in internal energy, ∆U=0, hence from the first law q = -W In such case, the work done in the expansion of n moles of a gas from volume V1 to V2 at constant temperature T is given by – 푊 = 푛푅푇푙푛(푉2) 푉1 푉2 푞푟푒푣 = −푊 = 푛푅푇푙푛( ) 푉1 Hence 푑푆 = 푑푞 = 1 푛푅푇푙푛 (푉2) = 푛푅푙푛 (푉2) 푇 푇 푉1 푉1 (Problem: 5 moles of ideal gas expand reversibly from volume of 8 dm3 to 80 dm3 at a temperature of 27oC. Calculate the change in entropy) Physical significance of Entropy: 1. Entropy as a measure of disorder of the system: All spontaneous processes, such as flow of heat from hot end to cold end, expansion of a gas in vacuum, diffusion of a solute from a concentrayed to a dilute solution, are accompanied by increase in disorder of the system. Spontaneous processes are acoompanied by increase in entropy as well as increase in disorder of the system. Thus entropy is regarded as a measure of the disorder of a system. 2. Entropy as a measure of probability: All spontaneous processes leads to increase in entropy. When a process is spontaneous, that means a system undergoes a change from less probable to a more probable state. It appears therefore that there is a close relationship between entropy and thermodynamic probability W. This relationship was expressed by S= k lnW (k is boltzman constant) Work and free energy function: The Helmholtz free energy or work function, A=U-TS For Isothermal reversible change, ∆AT=∆U-T∆S = ∆U- q = Wmax The work function A is a thermodynamic property of the system. Its decrease gives the maximum amount of work available during isothermal transformation. If the change is not Isothermal, A=U-TS dA = du-TdS-SdT dA= dU-dq-SdT dA= -PdV-SdT For Isochoric process, (푑퐴) = −푆 푑푇 푉 For isothermal process, (푑퐴) = −푃 푑푉 푇 For isothermal reversible change: G = H-TS = U+PV-TS ∆G = ∆U+P∆V+V∆P-T∆S-S∆T ∆GP,T = ∆U+P∆V-T∆S = ∆U+P∆V+V∆P- q = P∆V –W P∆V is the mechanical work involved in the system itself during transformation and W denotes the maximum output. So, W-P∆V is the amount of work received for any external use, exclusive of the mechanical work during transformation of the system Gibbs free energy is a property whose decrease is the measure of external work available is the measure of external work available during the transformation of the system G= H-TS G=U+PV-TS dG=Du+PdV+VdP-TdS-SdT in reversible process, dU+PdV=TdS So, dG=VdP-SdT For an isobaric process, (푑퐺) = −푆 푑푇 푃 For an isothermal process, (푑퐺) = 푉 푑푃 푇 .
Load more

Recommended publications
  • Isobaric Expansion Engines: New Opportunities in Energy Conversion for Heat Engines, Pumps and Compressors
    energies Concept Paper Isobaric Expansion Engines: New Opportunities in Energy Conversion for Heat Engines, Pumps and Compressors Maxim Glushenkov 1, Alexander Kronberg 1,*, Torben Knoke 2 and Eugeny Y. Kenig 2,3 1 Encontech B.V. ET/TE, P.O. Box 217, 7500 AE Enschede, The Netherlands; [email protected] 2 Chair of Fluid Process Engineering, Paderborn University, Pohlweg 55, 33098 Paderborn, Germany; [email protected] (T.K.); [email protected] (E.Y.K.) 3 Chair of Thermodynamics and Heat Engines, Gubkin Russian State University of Oil and Gas, Leninsky Prospekt 65, Moscow 119991, Russia * Correspondence: [email protected] or [email protected]; Tel.: +31-53-489-1088 Received: 12 December 2017; Accepted: 4 January 2018; Published: 8 January 2018 Abstract: Isobaric expansion (IE) engines are a very uncommon type of heat-to-mechanical-power converters, radically different from all well-known heat engines. Useful work is extracted during an isobaric expansion process, i.e., without a polytropic gas/vapour expansion accompanied by a pressure decrease typical of state-of-the-art piston engines, turbines, etc. This distinctive feature permits isobaric expansion machines to serve as very simple and inexpensive heat-driven pumps and compressors as well as heat-to-shaft-power converters with desired speed/torque. Commercial application of such machines, however, is scarce, mainly due to a low efficiency. This article aims to revive the long-known concept by proposing important modifications to make IE machines competitive and cost-effective alternatives to state-of-the-art heat conversion technologies. Experimental and theoretical results supporting the isobaric expansion technology are presented and promising potential applications, including emerging power generation methods, are discussed.
    [Show full text]
  • Section 15-6: Thermodynamic Cycles
    Answer to Essential Question 15.5: The ideal gas law tells us that temperature is proportional to PV. for state 2 in both processes we are considering, so the temperature in state 2 is the same in both cases. , and all three factors on the right-hand side are the same for the two processes, so the change in internal energy is the same (+360 J, in fact). Because the gas does no work in the isochoric process, and a positive amount of work in the isobaric process, the First Law tells us that more heat is required for the isobaric process (+600 J versus +360 J). 15-6 Thermodynamic Cycles Many devices, such as car engines and refrigerators, involve taking a thermodynamic system through a series of processes before returning the system to its initial state. Such a cycle allows the system to do work (e.g., to move a car) or to have work done on it so the system can do something useful (e.g., removing heat from a fridge). Let’s investigate this idea. EXPLORATION 15.6 – Investigate a thermodynamic cycle One cycle of a monatomic ideal gas system is represented by the series of four processes in Figure 15.15. The process taking the system from state 4 to state 1 is an isothermal compression at a temperature of 400 K. Complete Table 15.1 to find Q, W, and for each process, and for the entire cycle. Process Special process? Q (J) W (J) (J) 1 ! 2 No +1360 2 ! 3 Isobaric 3 ! 4 Isochoric 0 4 ! 1 Isothermal 0 Entire Cycle No 0 Table 15.1: Table to be filled in to analyze the cycle.
    [Show full text]
  • Thermodynamics I - Enthalpy
    CHEM 2880 - Kinetics Thermodynamics I - Enthalpy Tinoco Chapter 2 Secondary Reference: J.B. Fenn, Engines, Energy and Entropy, Global View Publishing, Pittsburgh, 2003. 1 CHEM 2880 - Kinetics Thermodynamics • An essential foundation for understanding physical and biological sciences. • Relationships and interconversions between various forms of energy (mechanical, electrical, chemical, heat, etc) • An understanding of the maximum efficiency with which we can transform one form of energy into another • Preferred direction by which a system evolves, i.e. will a conversion (reaction) go or not • Understanding of equilibrium • It is not based on the ideas of molecules or atoms. A linkage between these and thermo can be achieved using statistical methods. • It does not tell us about the rate of a process (how fast). Domain of kinetics. 2 CHEM 2880 - Kinetics Surroundings, boundaries, system When considering energy relationships it is important to define your point of reference. 3 CHEM 2880 - Kinetics Types of Systems Open: both mass and Closed: energy can be energy may leave and enter exchanged no matter can enter or leave Isolated: neither mass nor energy can enter or leave. 4 CHEM 2880 - Kinetics Energy Transfer Energy can be transferred between the system and the surroundings as heat (q) or work (w). This leads to a change in the internal energy (E or U) of the system. Heat • the energy transfer that occurs when two bodies at different temperatures come in contact with each other - the hotter body tends to cool while the cooler one warms
    [Show full text]
  • The First Law of Thermodynamics Continued Pre-Reading: §19.5 Where We Are
    Lecture 7 The first law of thermodynamics continued Pre-reading: §19.5 Where we are The pressure p, volume V, and temperature T are related by an equation of state. For an ideal gas, pV = nRT = NkT For an ideal gas, the temperature T is is a direct measure of the average kinetic energy of its 3 3 molecules: KE = nRT = NkT tr 2 2 2 3kT 3RT and vrms = (v )av = = r m r M p Where we are We define the internal energy of a system: UKEPE=+∑∑ interaction Random chaotic between atoms motion & molecules For an ideal gas, f UNkT= 2 i.e. the internal energy depends only on its temperature Where we are By considering adding heat to a fixed volume of an ideal gas, we showed f f Q = Nk∆T = nR∆T 2 2 and so, from the definition of heat capacity Q = nC∆T f we have that C = R for any ideal gas. V 2 Change in internal energy: ∆U = nCV ∆T Heat capacity of an ideal gas Now consider adding heat to an ideal gas at constant pressure. By definition, Q = nCp∆T and W = p∆V = nR∆T So from ∆U = Q W − we get nCV ∆T = nCp∆T nR∆T − or Cp = CV + R It takes greater heat input to raise the temperature of a gas a given amount at constant pressure than constant volume YF §19.4 Ratio of heat capacities Look at the ratio of these heat capacities: we have f C = R V 2 and f + 2 C = C + R = R p V 2 so C p γ = > 1 CV 3 For a monatomic gas, CV = R 3 5 2 so Cp = R + R = R 2 2 C 5 R 5 and γ = p = 2 = =1.67 C 3 R 3 YF §19.4 V 2 Problem An ideal gas is enclosed in a cylinder which has a movable piston.
    [Show full text]
  • Thermodynamic Potentials
    THERMODYNAMIC POTENTIALS, PHASE TRANSITION AND LOW TEMPERATURE PHYSICS Syllabus: Unit II - Thermodynamic potentials : Internal Energy; Enthalpy; Helmholtz free energy; Gibbs free energy and their significance; Maxwell's thermodynamic relations (using thermodynamic potentials) and their significance; TdS relations; Energy equations and Heat Capacity equations; Third law of thermodynamics (Nernst Heat theorem) Thermodynamics deals with the conversion of heat energy to other forms of energy or vice versa in general. A thermodynamic system is the quantity of matter under study which is in general macroscopic in nature. Examples: Gas, vapour, vapour in contact with liquid etc.. Thermodynamic stateor condition of a system is one which is described by the macroscopic physical quantities like pressure (P), volume (V), temperature (T) and entropy (S). The physical quantities like P, V, T and S are called thermodynamic variables. Any two of these variables are independent variables and the rest are dependent variables. A general relation between the thermodynamic variables is called equation of state. The relation between the variables that describe a thermodynamic system are given by first and second law of thermodynamics. According to first law of thermodynamics, when a substance absorbs an amount of heat dQ at constant pressure P, its internal energy increases by dU and the substance does work dW by increase in its volume by dV. Mathematically it is represented by 풅푸 = 풅푼 + 풅푾 = 풅푼 + 푷 풅푽….(1) If a substance absorbs an amount of heat dQ at a temperature T and if all changes that take place are perfectly reversible, then the change in entropy from the second 풅푸 law of thermodynamics is 풅푺 = or 풅푸 = 푻 풅푺….(2) 푻 From equations (1) and (2), 푻 풅푺 = 풅푼 + 푷 풅푽 This is the basic equation that connects the first and second laws of thermodynamics.
    [Show full text]
  • Heat Capacity Ratio of Gases
    Heat Capacity Ratio of Gases Carson Hasselbrink [email protected] Office Hours: Mon 10-11am, Beaupre 360 1 Purpose • To determine the heat capacity ratio for a monatomic and a diatomic gas. • To understand and mathematically model reversible & irreversible adiabatic processes for ideal gases. • To practice error propagation for complex functions. 2 Key Physical Concepts • Heat capacity is the amount of heat required to raise the temperature of an object or substance one degree 풅풒 푪 = 풅푻 • Heat Capacity Ratio is the ratio of specific heats at constant pressure and constant volume 퐶푝 훾 = 퐶푣 휕퐻 휕퐸 Where 퐶 = ( ) and 퐶 = ( ) 푝 휕푇 푝 푣 휕푇 푣 • An adiabatic process occurs when no heat is exchanged between the system and the surroundings 3 Theory: Heat Capacity 휕퐸 • Heat Capacity (Const. Volume): 퐶 = ( ) /푛 푣,푚 휕푇 푣 3푅푇 3푅 – Monatomic: 퐸 = , so 퐶 = 푚표푛푎푡표푚푖푐 2 푣,푚 2 5푅푇 5푅 – Diatomic: 퐸 = , so 퐶 = 푑푖푎푡표푚푖푐 2 푣,푚 2 • Heat Capacity Ratio: 퐶푝,푚 = 퐶푣,푚 + 푅 퐶푝,푚 푅 훾 = = 1 + 퐶푣,푚 퐶푣,푚 푃 [ln 1 ] 푃2 – Reversible: 훾 = 푃 [ln 1 ] 푃3 푃 [ 1 −1] 푃2 – Irreversible: 훾 = 푃 [ 1 −1] 푃3 • Diatomic heat capacity > Monatomic Heat Capacity 4 Theory: Determination of Heat Capacity Ratio • We will subject a gas to an adiabatic expansion and then allow the gas to return to its original temperature via an isochoric process, during which time it will cool. • This expansion and warming can be modeled in two different ways. 5 Reversible Expansion (Textbook) • Assume that pressure in carboy (P1) and exterior pressure (P2) are always close enough that entire process is always in equilibrium • Since system is in equilibrium, each step must be reversible 6 Irreversible Expansion (Lab Syllabus) • Assume that pressure in carboy (P1) and exterior pressure (P2) are not close enough; there is sudden deviation in pressure; the system is not in equilibrium • Since system is not in equilibrium, the process becomes irreversible.
    [Show full text]
  • 12/8 and 12/10/2010
    PY105 C1 1. Help for Final exam has been posted on WebAssign. 2. The Final exam will be on Wednesday December 15th from 6-8 pm. First Law of Thermodynamics 3. You will take the exam in multiple rooms, divided as follows: SCI 107: Abbasi to Fasullo, as well as Khajah PHO 203: Flynn to Okuda, except for Khajah SCI B58: Ordonez to Zhang 1 2 Heat and Work done by a Gas Thermodynamics Initial: Consider a cylinder of ideal Thermodynamics is the study of systems involving gas at room temperature. Suppose the piston on top of energy in the form of heat and work. the cylinder is free to move vertically without friction. When the cylinder is placed in a container of hot water, heat Equilibrium: is transferred into the cylinder. Where does the heat energy go? Why does the volume increase? 3 4 The First Law of Thermodynamics The First Law of Thermodynamics The First Law is often written as: Some of the heat energy goes into raising the temperature of the gas (which is equivalent to raising the internal energy of the gas). The rest of it does work by raising the piston. ΔEQWint =− Conservation of energy leads to: QEW=Δ + int (the first law of thermodynamics) This form of the First Law says that the change in internal energy of a system is Q is the heat added to a system (or removed if it is negative) equal to the heat supplied to the system Eint is the internal energy of the system (the energy minus the work done by the system (usually associated with the motion of the atoms and/or molecules).
    [Show full text]
  • Chapter 20 -- Thermodynamics
    ChapterChapter 2020 -- ThermodynamicsThermodynamics AA PowerPointPowerPoint PresentationPresentation byby PaulPaul E.E. TippensTippens,, ProfessorProfessor ofof PhysicsPhysics SouthernSouthern PolytechnicPolytechnic StateState UniversityUniversity © 2007 THERMODYNAMICSTHERMODYNAMICS ThermodynamicsThermodynamics isis thethe studystudy ofof energyenergy relationshipsrelationships thatthat involveinvolve heat,heat, mechanicalmechanical work,work, andand otherother aspectsaspects ofof energyenergy andand heatheat transfer.transfer. Central Heating Objectives:Objectives: AfterAfter finishingfinishing thisthis unit,unit, youyou shouldshould bebe ableable to:to: •• StateState andand applyapply thethe first andand second laws ofof thermodynamics. •• DemonstrateDemonstrate youryour understandingunderstanding ofof adiabatic, isochoric, isothermal, and isobaric processes.processes. •• WriteWrite andand applyapply aa relationshiprelationship forfor determiningdetermining thethe ideal efficiency ofof aa heatheat engine.engine. •• WriteWrite andand applyapply aa relationshiprelationship forfor determiningdetermining coefficient of performance forfor aa refrigeratior.refrigeratior. AA THERMODYNAMICTHERMODYNAMIC SYSTEMSYSTEM •• AA systemsystem isis aa closedclosed environmentenvironment inin whichwhich heatheat transfertransfer cancan taketake place.place. (For(For example,example, thethe gas,gas, walls,walls, andand cylindercylinder ofof anan automobileautomobile engine.)engine.) WorkWork donedone onon gasgas oror workwork donedone byby gasgas INTERNALINTERNAL
    [Show full text]
  • Thermodynamics of the Heat Engine
    Thermodynamics of the Heat Engine Waqas Mahmood, Salman Mahmood Qazi and Muhammad Sabieh Anwar April 20, 2011 The experiment provides an introduction to thermodynamics. Our principle objec- tive in this experiment is to understand and experimentally validate concepts such as pressure, force, work done, energy, thermal eciency and mechanical eciency. We will verify gas laws and make a heat engine using glass syringes. A highly inter- esting background resource for this experiment is selected material from Bueche's book [1]. The experimental idea is extracted from [2]. KEYWORDS Temperature Pressure Force Work Internal Energy Thermal Eciency Mechanical Eciency Data Acquisition Heat Engine Carnot Cycle Transducer Second law of thermodynamics APPROXIMATE PERFORMANCE TIME 6 hours 1 Conceptual Objectives In this experiment, we will, 1. learn about the rst and second laws of thermodynamics, 2. learn the practical demonstration of gas laws, 3. learn how to calculate the work done on and by the system, 4. correlate proportionalities between pressure, volume and temperature by equations and graphs, 5. make a heat engine using glass syringes, and 6. make a comparison between thermodynamic and mechanical eciencies. 2 Experimental Objectives The experimental objectives include, Salman, a student of Electronics at the Government College University worked as an intern in the Physics Lab. 1 1. a veri cation of Boyle's and Charles's laws, 2. use of the second law of thermodynamics to calculate the internal energy of a gas which is impossible to directly measure, 3. making a heat engine, 4. using transducers for measuring pressure, temperature and volume, and 5. tracing thermodynamical cycles.
    [Show full text]
  • 17.Examples of the 1St Law Rev2.Nb
    17. Examples of the First Law Introduction and Summary The First Law of Thermodynamics is basically a statement of Conservation of Energy. The total energy of a thermodynamic system is called the Internal Energy U. A system can have its Internal Energy changed (DU) in two major ways: (1) Heat Q > 0 can flow into the system from the surroundings, in which case the change in internal energy of the system increases: DU = Q. (2) The system can do work W > 0 on the surroundings, in which case the internal energy of the system decreases: DU = - W. Generally, the system interacts with the surroundings by exchanging both heat Q and doing work W, and the internal energy changes DU = Q - W This is the first law of thermodynamics and in it, W is the thermodynamic work done by the system on the surroundings. If the definition of mechanical work W were used instead of W, then the 1st Law would appear DU = Q + W because doing work on the system by the surroundings would increase the internal energy of the system DU = W. The 1st Law is simply the statement that the internal energy DU of a system can change in two ways: through heat Q absorption where, for example, the temperature changes, or by the system doing work -W, where a macroscopic parameter like volume changes. Below are some examples of using the 1st Law. The Work Done and the Heat Input During an Isobaric Expansion Suppose a gas is inside a cylinder that has a movable piston. The gas is in contact with a heat reservoir that is at a higher temperature than the gas so heat Q flows into the gas from the reservoir.
    [Show full text]
  • Internal Energy
    PROGRAM OF “PHYSICS” Lecturer: Dr. DO Xuan Hoi Room A1. 503 E-mail : [email protected] PHYSICS 2 (FLUID MECHANICS AND THERMAL PHYSICS) 02 credits (30 periods) Chapter 1 Fluid Mechanics Chapter 2 Heat, Temperature and the Zeroth Law of Thermodynamics Chapter 3 Heat, Work and the First Law of Thermodynamics Chapter 4 The Kinetic Theory of Gases Chapter 5 Entropy and the Second Law of Thermodynamics Chapter 3 Heat, Work and the First Law of Thermodynamics 1. Work and Heat in Thermodynamic Processes 2. The First Law of Thermodynamics 3. Some Applications of The First Law of Thermodynamics 4. Energy transfer mechanisms 1. Work and Heat in Thermodynamic Processes State of a system . Description of the system in terms of state variables ►Pressure ►Volume ►Temperature ►Internal Energy . A macroscopic state of an isolated system can be specified only if the system is in internal thermal equilibrium Work ► Work is an important energy transfer mechanism in thermodynamic systems ► Heat is another energy transfer mechanism ► Example: gas cylinder with piston . The gas is contained in a cylinder with a moveable piston . The gas occupies a volume V and exerts pressure P on the walls of the cylinder and on the piston Work done by a gas ► Consider a gas contained in a cylinder fitted with a movable piston. ► At equilibrium, the gas occupies a volume V and exerts a uniform pressure P on the cylinder’s walls and on the piston. If the piston has a cross-sectional area A, force exerted by the gas on the piston is : F PA ► When the gas expands quasi-statically
    [Show full text]
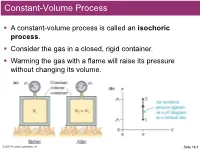
  • Constant-Volume Process
    Constant-Volume Process . A constant-volume process is called an isochoric process. Consider the gas in a closed, rigid container. Warming the gas with a flame will raise its pressure without changing its volume. © 2017 Pearson Education, Inc. Slide 18-1 Example 1 A constant-volume gas thermometer is placed in contact with a reference cell containing water at the triple point (T = 0.01ºC). After reaching equilibrium, the gas pressure is recorded as 55.78 kPa. The thermometer is then placed in contact with a sample of unknown temperature. After the thermometer reaches a new equilibrium, the gas pressure is 65.12 kPa. What is the temperature of this sample? © 2017 Pearson Education, Inc. Slide 18-2 QuickCheck A cylinder of gas has a frictionless but tightly sealed piston of mass M. A small flame heats the cylinder, causing the piston to slowly move upward. For the gas inside the cylinder, what kind of process is this? A. Isochoric B. Isobaric C. Isothermal D. Adiabatic © 2017 Pearson Education, Inc. Slide 18-3 Constant-Pressure Process . A constant-pressure process is called an isobaric process. Consider a cylinder of gas with a tight-fitting piston of mass M that can slide up and down but seals the container. In equilibrium, the gas pressure inside the cylinder is © 2017 Pearson Education, Inc. Slide 18-4 QuickCheck A cylinder of gas has a frictionless but tightly sealed piston of mass M. The gas temperature is increased from an initial 27ºC to a final 127ºC. What is the final-to-initial volume ratio Vf /Vi? A.
    [Show full text]