Alex K Chen, Atms 552, HW 9

Fake data set:

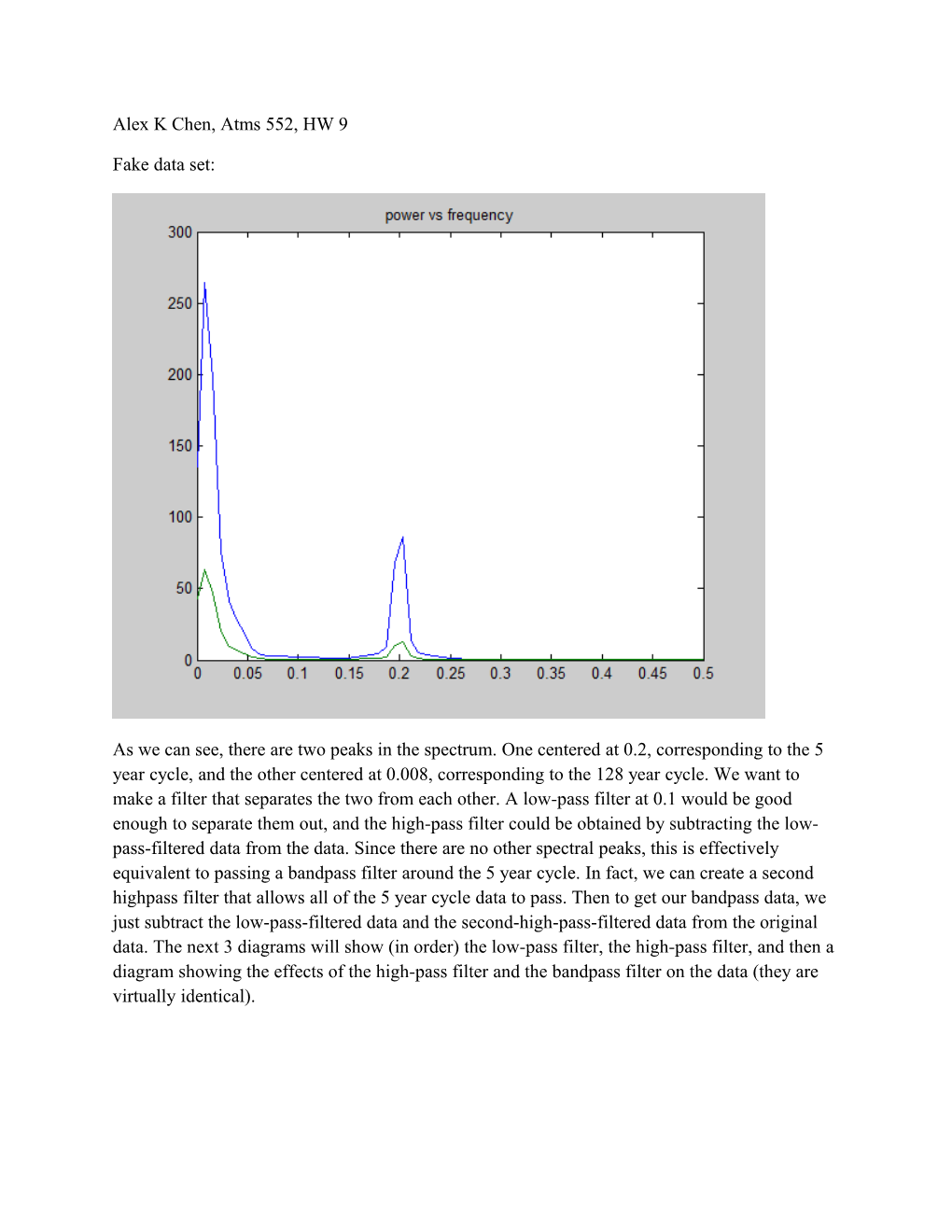
As we can see, there are two peaks in the spectrum. One centered at 0.2, corresponding to the 5 year cycle, and the other centered at 0.008, corresponding to the 128 year cycle. We want to make a filter that separates the two from each other. A low-pass filter at 0.1 would be good enough to separate them out, and the high-pass filter could be obtained by subtracting the low- pass-filtered data from the data. Since there are no other spectral peaks, this is effectively equivalent to passing a bandpass filter around the 5 year cycle. In fact, we can create a second highpass filter that allows all of the 5 year cycle data to pass. Then to get our bandpass data, we just subtract the low-pass-filtered data and the second-high-pass-filtered data from the original data. The next 3 diagrams will show (in order) the low-pass filter, the high-pass filter, and then a diagram showing the effects of the high-pass filter and the bandpass filter on the data (they are virtually identical).

We can see here that the band-passed data is the same as the data that we got from subtracting the low-pass data from original data. Here, we can also see that the band-passed data does indeed have a 5 year cycle, as it oscillates twice per 10-unit interval.

The low-pass filter is dashed blue. The high-frequency variance corresponding to the 5-year curve is green. We can see that the high-frequency variance is weak for years when the low- passed data is strong, and strong for years where the low-passed data is weak. We can also see that the high-frequency variance oscillates a lot more than the low-frequency variance, as would be predicted from its frequency. In fact, the high-frequency variance effectively acts like as spike train, where it fires many spikes when it is active (in the absence of the low-frequency variance).

If we try to extend this analysis to more data, we can see this:

As we can see, the two curves still have similar general waveforms throughout extended portions of time (the waveforms are effectively identical over the portion of the timescale that is shared between the three plots above). The low-passed dashed-blue alternates between negative and positive, and is usually inversely associated with the presence of spike trains on the green curve.

How do we develop our compositing hypothesis? We split the data several times over, and then examine if our patterns are consistent even on longer timescales (with the timescale included). We also want to see if our general patterns are consistent on scales disjoint from our original scale (although signals are often powerful on some timescales and not other others – this is known as a transition point, and compositing analysis allows us to split transition points up if averaging out the data could kill a possible pattern. This is not an issue here, however.). Consistency over multiple timescales is generally a sign of a correct hypothesis. Could we learn this from Fourier spectral analysis? Probably not, since while we can explain the significance of the periodicities from Fourier spectral analysis, we cannot use Fourier spectral analysis to see the direct effect of the periodicities on the data (where a particular period has its maximum effect on the data, for example). This we can do with filtering, and so we know (from filtering) that the two primary frequencies affect the data on different years from each other. We could use it to find the phase lag between the two functions though (but it still wouldn’t give out the exact impacts).

Real data set:

In this diagram, red is the red noise fit to the blue curve, and green is the 99% confidence interval for the null hypothesis of red noise(we still assume a smoothing factor of 1.2, as we have not smoothed with the Butterworth filter yet). Unless we can find a null hypothesis of a distribution that is not red noise, we cannot show two separate peaks using a priori statistics. The spectrum here is a very poor fit to the red noise distribution, since the second peak is larger in magnitude than the first peak. As a result, even the minimum of the blue curve (in between the two peaks) is “significant”. Which, of course, is absurd.

PSD peaks:

%3 000 000 / 3500 = 857.142857 %893 samples in time data %sampling of

Peak at 0.085 => 11.76 time pts

3500 years per time pt, so 41,160 years. This corresponds to the 40,000 year variability.

Peak at 0.0385 => 26 time pts

91,000 years

For the f vs P plot, first peak has period of 89,514 years. This effectively corresponds to the 100,000 year variability.

To pass the 100,000 year variability, we want to put a low-pass filter at 0.07, where the power is the lowest (in between the two separate signals)

Green curve is high-pass, and dashed-blue is low passed, as usual. To pass the 40,000 year variability, we want to high-pass the data at 0.07. For the last two plots,this shows up in data as green, since our code already set xhi = x – xlow. Since there are only two real peaks (and an effective absence of signal elsewhere), our high-pass filter can effectively be the complement of our low-pass filter. As we can see, the green curves vary much more than the blue curves. This is expected, as our green curves have a lower period.

So what does filtering tell us that spectral analysis does not? Here, it shows us the magnitude of the effect of the cycles on the data. Spectral analysis only tells us that the cycles exist. Here, we see that the contribution from the 40,000 year variability is small but distinct, and that the contribution from the 100,000 year variability is large, but not much more distinct than the 40,000 year variability.