8Th Grade Curriculum Document

8th Grade Curriculum Document Original Development: Summer 2013

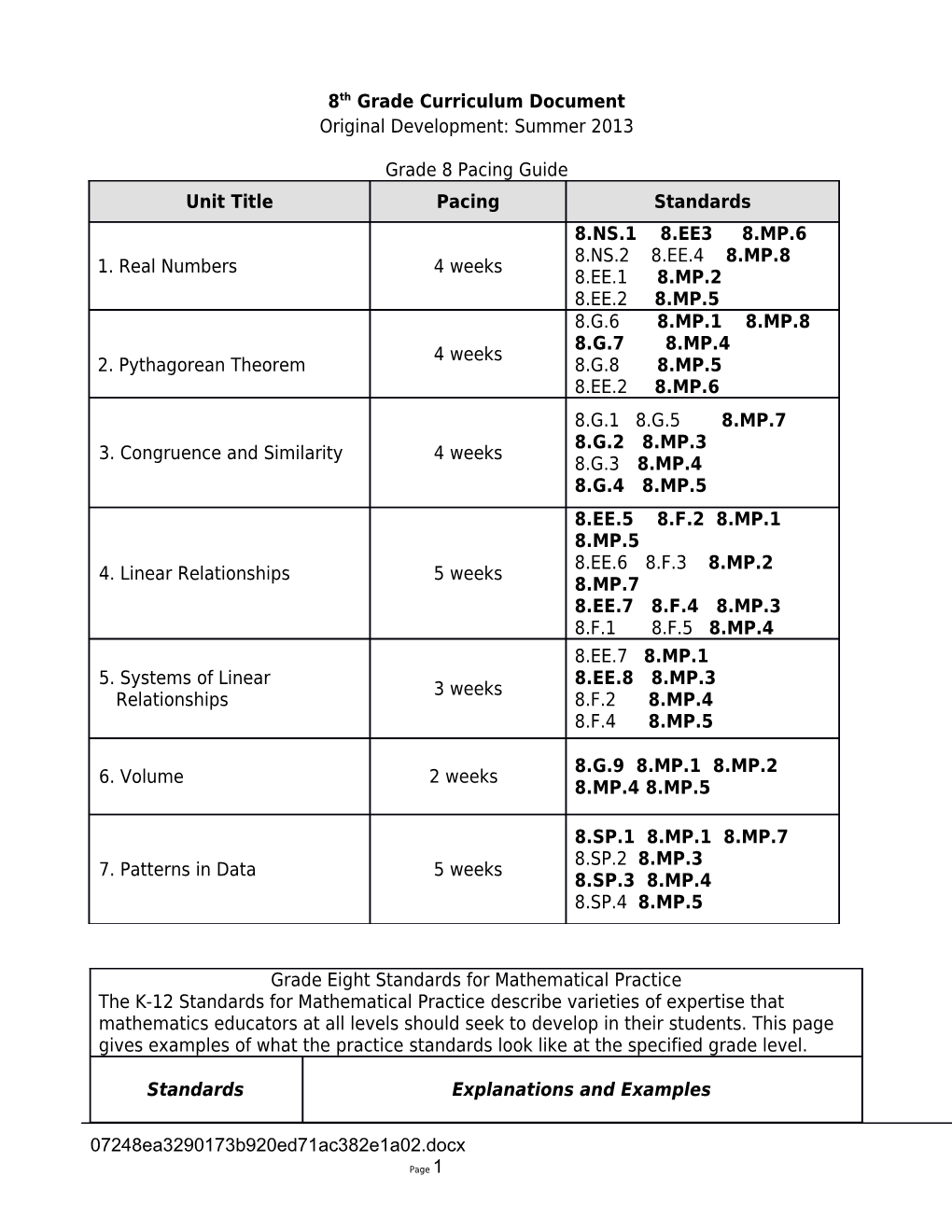
Grade 8 Pacing Guide Unit Title Pacing Standards 8.NS.1 8.EE3 8.MP.6 8.NS.2 8.EE.4 8.MP.8 1. Real Numbers 4 weeks 8.EE.1 8.MP.2 8.EE.2 8.MP.5 8.G.6 8.MP.1 8.MP.8 8.G.7 8.MP.4 4 weeks 2. Pythagorean Theorem 8.G.8 8.MP.5 8.EE.2 8.MP.6 8.G.1 8.G.5 8.MP.7 8.G.2 8.MP.3 3. Congruence and Similarity 4 weeks 8.G.3 8.MP.4 8.G.4 8.MP.5 8.EE.5 8.F.2 8.MP.1 8.MP.5 8.EE.6 8.F.3 8.MP.2 4. Linear Relationships 5 weeks 8.MP.7 8.EE.7 8.F.4 8.MP.3 8.F.1 8.F.5 8.MP.4 8.EE.7 8.MP.1 5. Systems of Linear 8.EE.8 8.MP.3 3 weeks Relationships 8.F.2 8.MP.4 8.F.4 8.MP.5

8.G.9 8.MP.1 8.MP.2 6. Volume 2 weeks 8.MP.4 8.MP.5

8.SP.1 8.MP.1 8.MP.7 8.SP.2 8.MP.3 7. Patterns in Data 5 weeks 8.SP.3 8.MP.4 8.SP.4 8.MP.5

Grade Eight Standards for Mathematical Practice The K-12 Standards for Mathematical Practice describe varieties of expertise that mathematics educators at all levels should seek to develop in their students. This page gives examples of what the practice standards look like at the specified grade level.

Standards Explanations and Examples

07248ea3290173b920ed71ac382e1a02.docx Page 1 Students are expected In grade 8, students solve real world problems through the to: application of algebraic and geometric concepts. Students seek 1. Make sense of the meaning of a problem and look for efficient ways to problems and represent and solve it. They may check their thinking by asking persevere in solving themselves, “What is the most efficient way to solve the them. problem?”, “Does this make sense?”, and “Can I solve the problem in a different way?” Students are expected In grade 8, students represent a wide variety of real world to:. contexts through the use of real numbers and variables in 2. Reason abstractly mathematical expressions, equations, and inequalities. They and quantitatively. examine patterns in data and assess the degree of linearity of functions. Students contextualize to understand the meaning of the number or variable as related to the problem and decontextualize to manipulate symbolic representations by applying properties of operations. Students are expected In grade 8, students construct arguments using verbal or to: written explanations accompanied by expressions, equations, 3. Construct viable inequalities, models, and graphs, tables, and other data arguments and displays (i.e. box plots, dot plots, histograms, etc.). They further critique the refine their mathematical communication skills through reasoning of others. mathematical discussions in which they critically evaluate their own thinking and the thinking of other students. They pose questions like “How did you get that?”, “Why is that true?” “Does that always work?” They explain their thinking to others and respond to others’ thinking. Students are expected In grade 8, students model problem situations symbolically, to: graphically,tabularly, and contextually. Students form 4. Model with expressions, equations, or inequalities from real world contexts mathematics. and connect symbolic and graphical representations. Students solve systems of linear equations and compare properties of functions provided in different forms. Students use scatterplots to represent data and describe associations between variables. Students need many opportunities to connect and explain the connections between the different representations. They should be able to use all of these representations as appropriate to a problem context. Students are expected Students consider available tools (including estimation and to: technology) when solving a mathematical problem and decide 5. Use appropriate when certain tools might be helpful. For instance, students in tools strategically. grade 8 may translate a set of data given in tabular form to a graphical representation to compare it to another data set. Students might draw pictures, use applets, or write equations to show the relationships between the angles created by a transversal. Students are expected In grade 8, students continue to refine their mathematical to: communication skills by using clear and precise language in 6. Attend to their discussions with others and in their own reasoning. 07248ea3290173b920ed71ac382e1a02.docx Page 2 precision. Students use appropriate terminology when referring to the number system, functions, geometric figures, and data displays. Students are expected Students routinely seek patterns or structures to model and to: solve problems. In grade 8, students apply properties to 7. Look for and generate equivalent expressions and solve equations. Students make use of examine patterns in tables and graphs to generate equations structure. and describe relationships. Additionally, students experimentally verify the effects of transformations and describe them in terms of congruence and similarity Students are expected In grade 8, students use repeated reasoning to understand to: algorithms and make generalizations about patterns. Students 8. Look for and use iterative processes to determine more precise rational express regularity approximations for irrational numbers. During multiple in repeated opportunities to solve and model problems, they notice that the reasoning. slope of a line and rate of change are the same value. Students flexibly make connections between covariance, rates, and representations showing the relationships between quantities.

Unit 1: Real Numbers Subject/Course: Pre-Algebra Grade Level: 8th School Year: 2013-2014

Domain: Expressions and Equations Cluster: Work with radicals and integer exponents. Standard Code:  8.EE.1. Know and apply the properties of integer exponents to generate equivalent numerical expressions. For example, 32 × 3–5 = 3–3 = 1/33 = 1/27.  8.EE.2 Use square root and cube root symbols to represent solutions to equations of the form x² = p and x³ = p, where p is a positive rational number. Evaluate square roots of small perfect squares and cube roots of small perfect cubes. Know that √2 is irrational.  8.EE.3. Use numbers expressed in the form of a single digit times an integer power of 10 to estimate very large or very small quantities, and to express how many times as much one is than the other. (Apply/DOK 3)For example, estimate the population of the United States as 3 × 108 and the population of the world as 7 × 109, and determine that the world population is more than 20 times larger.  8.EE.4. Perform operations with numbers expressed in scientific notation, including problems where both decimal and scientific notation are used. Use scientific notation and choose units of appropriate size for measurements of very large or very small quantities (e.g., use millimeters per year for seafloor spreading). Interpret scientific notation that has been generated by technology. Integration of College and Career Readiness Anchor Standards for Reading Reading Standard & Craft and Structure(R) Writing Standard 4. Interpret words and phrases as they are used in a text, and/or Math including determining technical, connotative, and figurative Practice meanings, and analyze how specific word choices shape meaning including CODE or tone. College and Career Readiness Anchor Standards for Writing Range of Writing(W) 10. Write routinely over extended time frames (time for research, reflection, and revision) and shorter time frames (a single sitting or a day or two) for a range of tasks, purposes, and audiences. The Mathematical Practices: 1. Make sense of problems and persevere in solving them. 2. Reason abstractly and quantitatively. 07248ea3290173b920ed71ac382e1a02.docx Page 4 3. Construct viable arguments and critique the reasoning of others. 4. Model with mathematics. 5. Use appropriate tools strategically. 6. Attend to precision. 7. Look for and make use of structure. 8. Look for and express regularity in repeated reasoning. Technology Standard: including CODE ELP Standard: Completed by SEI/ELP teachers (later) including CODE

07248ea3290173b920ed71ac382e1a02.docx Page 5 Clarifications of Content Standard Academic Vocabulary: What academic vocabulary does the student need to know? Real Numbers, Rational Number, Irrational Numbers, Integer Number, Whole Numbers, Natural Numbers Exponents, Scientific Notation Declarative Knowledge: What concepts (facts, ideas, cause/effect) does the student need to KNOW?  Decimal expansion  Integer power of 10  Properties of integer exponents  Square root  Perfect square  Cube root  Perfect cube Procedural Skill: What procedures (steps, algorithms, tactics) does the student need to know HOW to DO?  KNOW (rational and irrational numbers)  UNDERSTAND (decimal expansion)  SHOW (decimal expansion repeats)  CONVERT (repeating decimal expansion to a rational number)  USE (integer power of 10) . ESTIMATE (large or small quantities) . EXPRESS (magnitude of numbers using powers of 10) (rational approximations of irrational numbers) . COMPARE (sizes of rational numbers) . LOCATE (rational numbers approximately on a number line) . ESTIMATE (value of expressions) (square root and cube root symbols) . REPRESENT (solutions to equations) (scientific notation) . REPRESENT (very large and very small numbers) . CHOOSE (units of appropriate size)  EVALUATE o (square roots of perfect squares) o (cube roots of perfect cubes)  KNOW/APPLY (properties of integer exponents) o GENERATE (equivalent numerical expressions)  CALCULATE/CONVERT (numbers expressed in scientific notation/decimal form)  INTERPRET(scientific notation generated by technology) Prerequisites: Use Hess’s Cognitive Rigor Matrix to “map” pre-requisite conceptual & procedure knowledge Students must know; 6.EE.1. Write and evaluate numerical expressions involving whole-number exponents.

7.NS.1. Apply and extend previous understandings of addition and subtraction to add 07248ea3290173b920ed71ac382e1a02.docx Page 6 and subtract rational numbers; represent addition and subtraction on a horizontal or vertical number line diagram. 7.NS.2. Apply and extend previous understandings of multiplication and division and of fractions to multiply and divide rational numbers. 7.EE.3. Solve multi-step real-life and mathematical problems posed with positive and negative rational numbers in any form (whole numbers, fractions, and decimals), using tools strategically. Apply properties of operations to calculate with numbers in any form; convert between forms as appropriate; and assess the reasonableness of answers using mental computation and estimation strategies

Assessments Provide one assessment item for each content standard (one standard per box). For each assessment include: 1) standard + descriptive title + (Rigor) 2) an actual assessment item or quality description of the assessment 3) connection to Rdg, Wrtg, or Math Practice (if appropriate) 8.NS.1 and 8.NS.2 (Apply/DOK 2) Compare the numbers x and y below. A)XY, c) X=Y

8.EE.3 (Apply/DOK 3) Question 5: 2.1×10-5 + 0.038×10-3 + 0.41×10-4 =

10-4 10-5 10-3 2.1×10-4

07248ea3290173b920ed71ac382e1a02.docx Page 7 This section completed per whole unit. (Its purpose is to focus on integrating the standards through resources & instructional strategies that focus on unit big ideas.) UNIT Resources & Instruction Primary text connections: List chapters, pages, etc. CJHS- Holt McDougal Course 3 (green)  Chapter 4 o 4-1 Exponents pg 162 o 4-2 Integer Exponents pg 166 o 4-3 Properties of Exponents pg 170 o 4-4 Scientific Notation pg 174 . Lab Multiply /Divide numbers in scientific notation pg 179 o 4-5 Squares and Square Roots pg 182 o 4-6 Estimating Square Roots pg 186 . Ext Simplifying Square Roots pg 190 . Lab Explore Cube Roots pg 192 . Lab Evaluate Powers and Roots pg 194 o 4-7 The Real Numbers pg 195 Supplemental Text Connections: List other school-purchased curriculum resources. Other materials available: List other useful resources, teacher-created, online, etc. http://maccss.ncdpi.wikispaces.net/file/view/CCSSMathTasks-Grade8.pdf http://www.free-test-online.com/ccss/grade8/grade8_numbers. Teaching the Common Core Math Standards with Hands on activies Jossey-Bass Teacher Instructional Strategies: Research-based strategies that “fit.”  Grouping students  Questioning techniques  Setting high expectations for all students  Providing visual aids  Varity of assessments  Varity of technology usage Integration of Technology: Specific examples that apply the technology standards in the content.

Integration of ELP Strategies: (Language, Grammar, etc) Completed by SEI/ELP teachers (later)

07248ea3290173b920ed71ac382e1a02.docx Page 8 Unit 2: Pythagorean Theorem Subject/Course: Pre-Algebra Grade Level: 8th School Year: 2013-2014

07248ea3290173b920ed71ac382e1a02.docx Page 10 Clarifications of Content Standard Academic Vocabulary: What academic vocabulary does the student need to know? Pythagorean Theorem, Coordinate Plane, Perfect Square, Perfect Cube, Square Root, Cube Root, Right Triangles Declarative Knowledge: What concepts (facts, ideas, cause/effect) does the student need to KNOW?  Pythagorean Theorem o Proof of and its converse  Coordinate system Procedural Skill: What procedures (steps, algorithms, tactics) does the student need to know HOW to DO?  APPLY (Pythagorean Theorem) o DETERMINE (unknown side lengths in right triangles) o FIND (distance between two points in a coordinate system)  EXPLAIN (a proof of the Pythagorean Theorem and its converse)  USE (square root and cube root symbols) . REPRESENT (solutions to equations)  EVALUATE o (square roots of perfect squares) o (cube roots of perfect cubes) Prerequisites: Use Hess’s Cognitive Rigor Matrix to “map” pre-requisite conceptual & procedure knowledge Students must know; 6.EE.1. Write and evaluate numerical expressions involving whole-number exponents. 6.EE.6. Use variables to represent numbers and write expressions when solving a real- world or mathematical problem; understand that a variable can represent an unknown number, or, depending on the purpose at hand, any number in a specified set. 7.EE.1. Apply properties of operations as strategies to add, subtract, factor, and expand linear expressions with rational coefficients. 7.EE.2. Understand that rewriting an expression in different forms in a problem context can shed light on the problem and how the quantities in it are related. 8.EE.1. Know and apply the properties of integer exponents to generate equivalent numerical expressions. Assessments Provide one assessment item for each content standard (one standard per box). For each assessment include: 1) standard + descriptive title + (Rigor) 2) an actual assessment item or quality description of the assessment 3) connection to Rdg, Wrtg, or Math Practice (if appropriate) 8.G.7 (Apply/DOK 3) The distance between the vertices A and G of the polygon ABCDEFGHI in the coordinate plane below is meters.

07248ea3290173b920ed71ac382e1a02.docx Page 11 07248ea3290173b920ed71ac382e1a02.docx Page 12 This section completed per whole unit. (Its purpose is to focus on integrating the standards through resources & instructional strategies that focus on unit big ideas.) UNIT Resources & Instruction Primary text connections: List chapters, pages, etc. CJHS- Holt McDougal Course 3 (green)  Chapter 4 o 4-8 The Pythagorean Theorem pg 200 o 4-9 Applying the Pythagorean Theorem and its converse pg 204

Teacher Instructional Strategies: Research-based strategies that “fit.”  Grouping students  Questioning techniques  Setting high expectations for all students  Providing visual aids  Varity of assessments  Varity of technology usage

Integration of Technology: Specific examples that apply the technology standards in the content.

Integration of ELP Strategies: (Language, Grammar, etc) Completed by SEI/ELP teachers (later)

07248ea3290173b920ed71ac382e1a02.docx Page 13 Unit 3: Congruence and Similarity Subject/Course: Pre-Algebra Grade Level: 8th School Year: 2013-2014

This section completed once per whole unit. (Its purpose is to clarify the unit’s big idea and connecting standards.) Big Ideas: Why is this learning important? What generalization or principle do you want to know/do? The big idea resides at the heart of the discipline, and has value beyond classroom. These may come from the cluster deconstructing process. Understand congruence and similarity using physical models, transparencies, or geometry software to show a series of transformations. Common Core Standards / State Standards Content Standard: Domain: Geometry including CODE + Cluster: Understand congruence and similarity using physical (Rigor) models, transparencies, or geometry software. Standard Code:  8.G.1 Verify experimentally the properties of rotations, reflections, and translations: o Lines are taken to lines, and line segments to line segments of the same length. o Angles are taken to angles of the same measure. o Parallel lines are taken to parallel lines.  8.G.2. Understand that a two-dimensional figure is congruent to another if the second can be obtained from the first by a sequence of rotations, reflections and translations; given two congruent figures, describe a sequence that exhibits the congruence between them. (Analyze/DOK 2)  8.G.3. Describe the effect of dilations, translations, rotations, and reflections on two-dimensional figures using coordinates.  8.G.4. Understand that a two-dimensional figure is similar to another if the second can be obtained from the first by a sequence of rotations, reflections, translations, and dilations; given two similar two-dimensional figures, describe a sequence that exhibits the similarity between them. (Analyze/DOK 2)  8.G.5. Use informal arguments to establish facts about the angle sum and exterior angle of triangles, about the angles created when parallel lines are cut by a transversal, and the angle-angle criterion for similarity of triangles. For example, arrange three copies of the same triangle so that the sum of the three angles appears to form a line, and give an argument in terms of transversals why this is so. 07248ea3290173b920ed71ac382e1a02.docx Page 14 Integration of College and Career Readiness Anchor Standards for Reading Reading Standard & Craft and Structure(R) Writing Standard 4. Interpret words and phrases as they are used in a text, and/or Math including determining technical, connotative, and figurative Practice meanings, and analyze how specific word choices shape meaning including CODE or tone. Integration of Knowledge and Ideas (R) 8. Delineate and evaluate the argument and specific claims in a text, including the validity of the reasoning as well as the relevance and sufficiency of the evidence. College and Career Readiness Anchor Standards for Writing Text Types and Purposes(W) 1.Write arguments to support claims in an analysis of substantive topics or texts, using valid reasoning and relevant and sufficient evidence. Range of Writing(W) 10.Write routinely over extended time frames (time for research, reflection, and revision) and shorter time frames (a single sitting or a day or two) for a range of tasks, purposes, and audiences. The Mathematical Practices: 1. Make sense of problems and persevere in solving them. 2. Reason abstractly and quantitatively. 3. Construct viable arguments and critique the reasoning of others. 4. Model with mathematics. 5. Use appropriate tools strategically. 6. Attend to precision. 7. Look for and make use of structure. 8. Look for and express regularity in repeated reasoning. Technology ET08-S1C1-01 Standard: Analyze and evaluate information to generate new ideas, including CODE processes or products. ELP Standard: Completed by SEI/ELP teachers (later) including CODE

07248ea3290173b920ed71ac382e1a02.docx Page 15 Clarifications of Content Standard Academic Vocabulary: What academic vocabulary does the student need to know? Congruence, Similarity, Translation, Dilation, Rotation, Reflection, Parallel, Transversal, Interior Angles, Exterior Angles, Informal Proof Declarative Knowledge: What concepts (facts, ideas, cause/effect) does the student need to KNOW?  Angle sum and exterior angle of triangles  Parallel lines cut by a transversal o Angles formed Angle-angle criterion for similar triangles Procedural Skill: What procedures (steps, algorithms, tactics) does the student need to know HOW to DO?  VERIFY (Experimentally properties of) o Rotations o Reflections o Translations o Dilations  UNDERSTAND (Congruence) o DESCRIBE (Sequence of rotations, reflections, translations)  UNDERSTAND (Similarity) o DESCRIBE (Sequence of rotations, reflections, translations, dilations) DESCRIBE (effect of dilations, translations, rotations and reflections using coordinates) PROVE (informally) o angle relationships in parallel lines cut by a transversal o sum of angles in a triangle = 180° Prerequisites: Use Hess’s Cognitive Rigor Matrix to “map” pre-requisite conceptual & procedure knowledge Students must know; 6.G.3. Draw polygons in the coordinate plane given coordinates for the vertices; use coordinates to find the length of a side joining points with the same first coordinate or the same second coordinate. Apply these techniques in the context of solving real-world and mathematical problems.

What transformation took place from Figure 1 to Figure 2?

07248ea3290173b920ed71ac382e1a02.docx Page 16 rotation 180° A counterclockwise around point B rotation 180° clockwise around point B D rotation 180° clockwise around point C C rotation 180° counterclockwise D around point A

8.G.4 (Apply/DOK 2) These two heptagons are similar. What is the value of x?

A x = 2 x = B 3.5 x = C 4.5 D x = 5

07248ea3290173b920ed71ac382e1a02.docx Page 17 This section completed per whole unit. (Its purpose is to focus on integrating the standards through resources & instructional strategies that focus on unit big ideas.) UNIT Resources & Instruction Primary text connections: List chapters, pages, etc. CJHS- Holt McDougal Course 3 (green)  Chapter 5 o 5-5 Similar Figures pg 246 . Lab Explore Dilations pg 250 o 5-6 Dilations pg 252  Chapter 7 o 7-5 Coordinate Geometry pg 353 o 7-6 Congruence pg 360 o 7-7 Transformations 364

Supplemental Text Connections: List other school-purchased curriculum resources. Other materials available: List other useful resources, teacher-created, online, etc. http://www.free-test-online.com/ccss/grade8/grade8_numbers. http://maccss.ncdpi.wikispaces.net/file/view/CCSSMathTasks-Grade8.pdf Teaching the Common Core Math Standards with Hands on activies Jossey-Bass Teacher Instructional Strategies: Research-based strategies that “fit.”  Grouping students  Questioning techniques  Setting high expectations for all students  Providing visual aids  Varity of assessments  Varity of technology usage

Integration of Technology: Specific examples that apply the technology standards in the content.  Investigating the relationship between angles and their measurements, students determine the angle of folds to create a pinwheel. Pinwheel - Investigating the Geometry of an Origami Octagon that Changes Shape Integration of ELP Strategies: (Language, Grammar, etc) Completed by SEI/ELP teachers (later)

07248ea3290173b920ed71ac382e1a02.docx Page 18 Unit 4: Linear Functions Subject/Course: Pre-Algebra Grade Level: 8th School Year: 2013-2014

This section completed once per whole unit. (Its purpose is to clarify the unit’s big idea and connecting standards.) Big Ideas: Why is this learning important? What generalization or principle do you want to know/do? The big idea resides at the heart of the discipline, and has value beyond classroom. These may come from the cluster deconstructing process. Understand the connections between proportional relationships, lines, and linear equations. Analyze and solve linear equations. Define, evaluate, and compare functions. Use functions to model relationships between quantities. Common Core Standards / State Standards Content Standard: Domain: Expressions and Equations including CODE + Cluster: Understand the connections between proportional (Rigor) relationships, lines, and linear equations. Standard Code:  8.EE.5. Graph proportional relationships, interpreting the unit rate as the slope of the graph. Compare two different proportional relationships represented in different ways. (Analyze/DOK 3) For example, compare a distance-time graph to a distance- time equation to determine which of two moving objects has greater speed.  8.EE.6. Use similar triangles to explain why the slope m is the same between any two distinct points on a non-vertical line in the coordinate plane; derive the equation y = mx for a line through the origin and the equation y = mx + b for a line intercepting the vertical axis at b. Domain: Expressions and Equations Cluster: Analyze and solve linear equations and pairs of simultaneous linear equations. Standard Code:  8.EE.7. Solve linear equations in one variable. (Analyze/DOK 3) o Give examples of linear equations in one variable with one solution, infinitely many solutions, or no solutions. Show which of these possibilities is the case by successively transforming the given equation into simpler forms, until an equivalent equation of the form x = a, a = a, or a = b results (where a and b are different numbers). o Solve linear equations with rational number coefficients, including equations whose 07248ea3290173b920ed71ac382e1a02.docx Page 19 solutions require expanding expressions using the distributive property and collecting like terms. Domain: Functions Cluster: Define, evaluate, and compare functions. Standard Code:  8.F.1. Understand that a function is a rule that assigns to each input exactly one output. The graph of a function is the set of ordered pairs consisting of an input and the corresponding output.  8.F.2. Compare properties of two functions each represented in a different way (algebraically, graphically, numerically in tables, or by verbal descriptions). (Analyze/DOK 3) For example, given a linear function represented by a table of values and a linear function represented by an algebraic expression, determine which function has the greater rate of change.  8.F.3.Interpret the equation y = mx + b as defining a linear function, whose graph is a straight line; give examples of functions that are not linear. For example, the function A = s² giving the area of a square as a function of its side length is not linear because its graph contains the points (1,1), (2,4) and (3,9), which are not on a straight line Domain: Functions Cluster: Use functions to model relationships between quantities. Standard Code:  8.F.4. Construct a function to model a linear relationship between two quantities. Determine the rate of change and initial value of the function from a description of a relationship or from two (x, y) values, including reading these from a table or from a graph. Interpret the rate of change and initial value of a linear function in terms of the situation it models, and in terms of its graph or a table of values. (Analyze/DOK 3)  8.F.5.Describe qualitatively the functional relationship between two quantities by analyzing a graph, (e.g. where the function is increasing or decreasing, linear or nonlinear). Sketch a graph that exhibits the qualitative features of a function that has been described verbally. Integration of College and Career Readiness Anchor Standards for Reading Reading Standard & Integration of Knowledge and Ideas(R) Writing Standard 7. Integrate and evaluate content presented in diverse media and/or Math and formats, including visually and quantitatively, as well as in Practice words including CODE College and Career Readiness Anchor Standards for Writing Range of Writing(W) 07248ea3290173b920ed71ac382e1a02.docx Page 20 10. Write routinely over extended time frames (time for research, reflection, and revision) and shorter time frames (a single sitting or a day or two) for a range of tasks, purposes, and audiences.

The Mathematical Practices: 1. Make sense of problems and persevere in solving them. 2. Reason abstractly and quantitatively. 3. Construct viable arguments and critique the reasoning of others. 4. Model with mathematics. 5. Use appropriate tools strategically. 6. Attend to precision. 7. Look for and make use of structure. 8. Look for and express regularity in repeated reasoning. Technology ET08-S1C2-02 Standard: Analyze system processes and outcomes using models or including CODE simulations. ET08-S1C2-03 Analyze and apply understanding of how one system, digital models or simulations operates by comparing it to another system of a different type that operates in a similar manner. ET08-S1C3-03 Draw conclusions that reflect clear and logical links between the trends and patterns and the interpretations made from them. ET08-S1C4-01 Create innovative products or projects using digital tools to express original ideas. ELP Standard: Completed by SEI/ELP teachers (later) including CODE

07248ea3290173b920ed71ac382e1a02.docx Page 21 Clarifications of Content Standard Academic Vocabulary: What academic vocabulary does the student need to know? Proportional Relationship, Unit Rate, Slope, Linear Relationship, Function, Coefficients, Solution Declarative Knowledge: What concepts (facts, ideas, cause/effect) does the student need to KNOW?  Proportional relationships  Unit rate  Slope (m)  Y-intercept (b)  Linear equations (y = mx and y = mx + b) o Rational Number Coefficients o One variable . One solution . Infinitely many solutions . No solutions  Equations into simple forms o Expanding Expressions o Distributive property o Combining Like terms  Functions o Properties . Linear . Non-linear o Input/Output o Ordered pairs  Linear/functional relationship  rate of change  initial value (function)  table  graph Similar triangles Procedural Skill: What procedures (steps, algorithms, tactics) does the student need to know HOW to DO?  GRAPH (proportional relationships)  INTERPRET (unit rate as slope)  COMPARE (proportional relationships)  EXPLAIN (why slope is the same between any two points on a non-vertical line)  DERIVE (linear equations (y = mx and y = mx + b)  SOLVE (linear equations)  GIVE (example of linear equations)  TRANSFORM (equations)  EXPAND (expressions) o Use (distributive property) o Collect (like terms)

07248ea3290173b920ed71ac382e1a02.docx Page 22  UNDERSTAND (function is a rule) o GRAPH (sets of ordered pairs)  COMPARE (functions) o Algebraically o Graphically o Numerically in tables o Verbal descriptions  CONSTRUCT (function) o Model (linear relationship)  DETERMINE (rate of change and initial value of function)  READ (table or graph)  INTERPRET o y = mx + b o rate of change and initial value of function  GIVE (examples of non-linear functions)  DESCRIBE (functional relationship between two quantities) DRAW (graph from a verbal description) Prerequisites: Use Hess’s Cognitive Rigor Matrix to “map” pre-requisite conceptual & procedure knowledge Students must know; 6.EE.6. Use variables to represent numbers and write expressions when solving a real- world or mathematical problem; understand that a variable can represent an unknown number, or, depending on the purpose at hand, any number in a specified set. 6.EE.7. Solve real-world and mathematical problems by writing and solving equations of the form x + p = q and px = q for cases in which p, q and x are all nonnegative rational numbers 6.EE.9. Use variables to represent two quantities in a real-world problem that change in relationship to one another; write an equation to express one quantity, thought of as the dependent variable, in terms of the other quantity, thought of as the independent variable. Analyze the relationship between the dependent and independent variables using graphs and tables, and relate these to the equation. 7.EE.1. Apply properties of operations as strategies to add, subtract, factor, and expand linear expressions with rational coefficients. 7.EE.3. Solve multi-step real-life and mathematical problems posed with positive and negative rational numbers in any form (whole numbers, fractions, and decimals), using tools strategically. Apply properties of operations to calculate with numbers in any form; convert between forms as appropriate; and assess the reasonableness of answers using mental computation and estimation strategies 7.RP.2. Recognize and represent proportional relationships between quantities.

07248ea3290173b920ed71ac382e1a02.docx Page 23 Two vehicles travel with constant speeds. Vehicle A speed is given in the graph below, while vehicle B speed is given by the equation vB = 61.2×t, where vB is measured in miles/hour and t is measured in hours.

The faster of the two vehicles is .

8.EE.7 (Analyze/DOK 3) Solve the following linear equation:

x = -6 x = -3 x = -1 x = 2

8.F.2 (Analyze/DOK 3)

Given the linear function f1 in the table below and the linear function f2 represented by the equation y = -3.2x +6, which of the functions has a greater rate of change? x y 0 1 1 -3 2 -7 3 -11 4 -15 f1 f2

07248ea3290173b920ed71ac382e1a02.docx Page 24 8.F.4 (Analyze/DOK 3)

Which equation represents the data in the table?

y = 3x - A 1 y = -3x - B 1 y = -3x C + 1 y = 3x - D 2

07248ea3290173b920ed71ac382e1a02.docx Page 25 This section completed per whole unit. (Its purpose is to focus on integrating the standards through resources & instructional strategies that focus on unit big ideas.) UNIT Resources & Instruction Primary text connections: List chapters, pages, etc. CJHS- Holt McDougal Course 3 (green)  Chapter 3 o 3-4 Functions pg 136 o 3-5 Equations, Tables, and Graphs pg 140 . Lab Explore Multiple representations pg 144  Chapter 11 o 11-1 Simplifying Algebraic Expressions pg 588 o 11-2 Solving Multi-Step Equations pg 592 o 11-3 Solving Equations with Variables on Both Sides pg 597  Chapter 12 o 12-1 Graphing Linear Equations pg 632 o 12-2 Slope of the Line pg 637 o 12-3 Using Slopes and Intercepts pg 642 . Lab Graph Equations in Slope Intercept Form pg 642 o 12-5 Direct Variation pg 654  Chapter 13 o 13-4 Linear Functions pg 700 Supplemental Text Connections: List other school-purchased curriculum resources. Other materials available: List other useful resources, teacher-created, online, etc. http://www.free-test-online.com/ccss/grade8/grade8_numbers. http://maccss.ncdpi.wikispaces.net/file/view/CCSSMathTasks-Grade8.pdf Teaching the Common Core Math Standards with Hands on activies Jossey-Bass Teacher Instructional Strategies: Research-based strategies that “fit.”  Grouping students  Questioning techniques  Setting high expectations for all students  Providing visual aids  Varity of assessments  Varity of technology usage Integration of Technology: Specific examples that apply the technology standards in the content. Students will independently work through activities, after completing activities group students (2 to 3). In groups students will share understanding and identify important concepts to be shared with whole group. Graphing Linear Equations (Note: teachers are required to create a free account.)

Students will investigate 3 different web activities. This activity will reinforce and strengthen understanding of math concept and help students develop ability to assess and defend choices.(Teacher adjustments for range of ability levels could include: Teacher created site evaluation form to student developed assessment.) Karappan Poochi - Algebra vs. The Cockroach Quia - Slope Jeopardy 07248ea3290173b920ed71ac382e1a02.docx Page 26 Math Warehouse - Interactive Slope HTML5 Applet

Students will examine a situation using a data collection device (motion detector) and a graphing calculator to determine if a situation displays linear behavior. (a)Students will connect a motion detector to a graphing calculator, start the data collection program, place detector so it can read the motion of a walker, mark the floor, and have one student walk away at slow and steady pace while detector collects the data. (b)Students will analyze data to determine if the motion represents linear behavior. Have students experiment with other types of movement - making predictions of outcomes and make comparisons with other motive behavior.

Using Excel or other spreadsheet tool or program, have students create function rules that model multiple linear relationships and display graphs for each. (a)Students will analyze graphs to determine F(x), constant rate of change, and explain relationship between the two quantities. Graphing Linear equations - How to directions

Integration of ELP Strategies: (Language, Grammar, etc) Completed by SEI/ELP teachers (later)

07248ea3290173b920ed71ac382e1a02.docx Page 27 Unit 5: System of Linear Equations Subject/Course: Pre-Algebra Grade Level: 8th School Year: 2013-2014

This section completed once per whole unit. (Its purpose is to clarify the unit’s big idea and connecting standards.) Big Ideas: Why is this learning important? What generalization or principle do you want to know/do? The big idea resides at the heart of the discipline, and has value beyond classroom. These may come from the cluster deconstructing process. Analyze and solve linear equations and pairs of simultaneous linear equations for mathematical and real world problems. Common Core Standards / State Standards Content Standard: Domain: Expressions and Equations including CODE + Cluster: Analyze and solve linear equations and pairs of (Rigor) simultaneous linear equations. Standard Code:  8.EE.7.Solve linear equations in one variable. o Give examples of linear equations in one variable with one solution, infinitely many solutions, or no solutions. Show which of these possibilities is the case by successively transforming the given equation into simpler forms, until an equivalent equation of the form x = a, a = a, or a = b results (where a and b are different numbers). o Solve linear equations with rational number coefficients, including equations whose solutions require expanding expressions using the distributive property and collecting like terms.  8.EE.8. Analyze and solve pairs of simultaneous linear equations. (Analyze/DOK 3) o Understand that solutions to a system of two linear equations in two variables correspond to points of intersection of their graphs, because points of intersection satisfy both equations simultaneously. o Solve systems of two linear equations in two variables algebraically, and estimate solutions by graphing the equations. Solve simple cases by inspection. For example, 3x + 2y = 5 and 3x + 2y = 6 have no solution because 3x + 2y cannot simultaneously be 5 and 6. o Solve real-world and mathematical problems leading to two linear equations in two variables. For example, given coordinates for two pairs of points, determine whether the 07248ea3290173b920ed71ac382e1a02.docx Page 28 line through the first pair of points intersects the line through the second pair. Domain: Functions Cluster: Define, evaluate, and compare functions. Standard Code: o 8.F.2. Compare properties of two functions each represented in a different way (algebraically, graphically, numerically in tables, or by verbal descriptions). For example, given a linear function represented by a table of values and a linear function represented by an algebraic expression, determine which function has the greater rate of change. Domain: Functions Cluster: Use functions to model relationships between quantities. Standard Code: o 8.F.4. Construct a function to model a linear relationship between two quantities. Determine the rate of change and initial value of the function from a description of a relationship or from two (x, y) values, including reading these from a table or from a graph. Interpret the rate of change and initial value of a linear function in terms of the situation it models, and in terms of its graph or a table of values. Integration of College and Career Readiness Anchor Standards for Reading Reading Standard & Integration of Knowledge and Ideas(R) Writing Standard 7. Integrate and evaluate content presented in diverse media and/or Math and formats, including visually and quantitatively, as well as in Practice words including CODE College and Career Readiness Anchor Standards for Writing Range of Writing(W) 10. Write routinely over extended time frames (time for research, reflection, and revision) and shorter time frames (a single sitting or a day or two) for a range of tasks, purposes, and audiences. The Mathematical Practices: 1. Make sense of problems and persevere in solving them. 2. Reason abstractly and quantitatively. 3. Construct viable arguments and critique the reasoning of others. 4. Model with mathematics. 5. Use appropriate tools strategically. 6. Attend to precision. 7. Look for and make use of structure. 8. Look for and express regularity in repeated reasoning. Technology ET08-S1C2-01 Standard: Summarize the relationship amongst interdependent elements of including CODE a digital model or simulation. 07248ea3290173b920ed71ac382e1a02.docx Page 29 ET08-S6C2-03 Apply formatting features while using spreadsheet programs to customize tables, charts, and graphs. ELP Standard: Completed by SEI/ELP teachers (later) including CODE

07248ea3290173b920ed71ac382e1a02.docx Page 30 Clarifications of Content Standard Academic Vocabulary: What academic vocabulary does the student need to know? Proportional Relationship, Unit Rate, Slope, Linear Relationship, Function, Coefficients, Solution (Same as Unit 4) Declarative Knowledge: What concepts (facts, ideas, cause/effect) does the student need to KNOW? Linear Equations (Simultaneous/system of) o Rational Number Coefficients . One variable . One solution . Many solutions . No solutions Equations into simpler forms o Expanding Expressions o Distributive Property o Combining Like Terms Function o Rate of change o Initial value (of a linear function) o Representation . Algebraically . Graphically . Numerically in tables . Verbal description Procedural Skill: What procedures (steps, algorithms, tactics) does the student need to know HOW to DO? o SOLVE (linear equations) o SHOW (simpler forms) o ANALYZE (linear equations) o UNDERSTAND (solutions) o SOLVE (systems of equations) o ESTIMATE (solutions) o GRAPH (equations) o SOLVE o (simple cases by inspection) o In context o CONSTRUCT (function) o DETERMINE (rate of change and initial value of the function) o READ (table and graph) o INTERPRET (rate of change and initial value of a linear function o COMPARE (functions represented differently) Prerequisites: Use Hess’s Cognitive Rigor Matrix to “map” pre-requisite conceptual & procedure knowledge Students must know; 6.EE.6. Use variables to represent numbers and write expressions when solving a real- world or mathematical problem; understand that a variable can represent an unknown 07248ea3290173b920ed71ac382e1a02.docx Page 31 number, or, depending on the purpose at hand, any number in a specified set. 6.EE.7. Solve real-world and mathematical problems by writing and solving equations of the form x + p = q and px = q for cases in which p, q and x are all nonnegative rational numbers 6.EE.9. Use variables to represent two quantities in a real-world problem that change in relationship to one another; write an equation to express one quantity, thought of as the dependent variable, in terms of the other quantity, thought of as the independent variable. Analyze the relationship between the dependent and independent variables using graphs and tables, and relate these to the equation. 7.EE.1. Apply properties of operations as strategies to add, subtract, factor, and expand linear expressions with rational coefficients. 7.EE.3. Solve multi-step real-life and mathematical problems posed with positive and negative rational numbers in any form (whole numbers, fractions, and decimals), using tools strategically. Apply properties of operations to calculate with numbers in any form; convert between forms as appropriate; and assess the reasonableness of answers using mental computation and estimation strategies 7.RP.2. Recognize and represent proportional relationships between quantities. Assessments Provide one assessment item for each content standard (one standard per box). For each assessment include: 1) standard + descriptive title + (Rigor) 2) an actual assessment item or quality description of the assessment 3) connection to Rdg, Wrtg, or Math Practice (if appropriate) 8.EE.8 (Analyze/DOK 3) : Solve the following system of linear equations: y = 3x y - x = 1 x = 1/2, y = 3/2 x = 1/2, y = -3/2 x = -1/2, y = 3/2 x = -1/2, y = -3/2

07248ea3290173b920ed71ac382e1a02.docx Page 32 This section completed per whole unit. (Its purpose is to focus on integrating the standards through resources & instructional strategies that focus on unit big ideas.) UNIT Resources & Instruction Primary text connections: List chapters, pages, etc. CJHS- Holt McDougal Course 3 (green)  Chapter 11 o Systems of Equations pg 612  Chapter 12 o Solving Systems of Linear Equations by Graphing pg 664

Integration of Technology: Specific examples that apply the technology standards in the content. Students will use a simulation to explore systems of linear equations, providing them an opportunity to explore the relationship between x, y values. Students explore by creating equations that demonstrate infinite solutions, one solution, or no solution. Students will analyze graphs and provide rationale for results. Students will use a spreadsheet program (i.e. Excel, Numbers) to solve simultaneous linear equations. Use formulas to solve for two equations and convert table values into a graph demonstrating their points of intersection. Integration of ELP Strategies: (Language, Grammar, etc) Completed by SEI/ELP teachers (later)

07248ea3290173b920ed71ac382e1a02.docx Page 33 Unit 6: Volume Subject/Course: Pre-Algebra Grade Level: 8th School Year: 2013-2014

07248ea3290173b920ed71ac382e1a02.docx Page 35 Clarifications of Content Standard Academic Vocabulary: What academic vocabulary does the student need to know? Volume, Cone, Cylinder, Spheres Declarative Knowledge: What concepts (facts, ideas, cause/effect) does the student need to KNOW? Formulas (volume) o Cones o Cylinders Spheres Procedural Skill: What procedures (steps, algorithms, tactics) does the student need to know HOW to DO?  Know (formulas for volumes)  Use (formulas for volumes) Solve (in context) Prerequisites: Use Hess’s Cognitive Rigor Matrix to “map” pre-requisite conceptual & procedure knowledge Conceptual Knowledge: What concepts does the student need prior to engaging in this standard? Students must know; 6.EE.6. Use variables to represent numbers and write expressions when solving a real- world or mathematical problem; understand that a variable can represent an unknown number, or, depending on the purpose at hand, any number in a specified set. 6.G.2. Find the volume of a right rectangular prism with fractional edge lengths by packing it with unit cubes of the appropriate unit fraction edge lengths, and show that the volume is the same as would be found by multiplying the edge lengths of the prism. Apply the formulas V = l w h and V = b h to find volumes of right rectangular prisms with fractional edge lengths in the context of solving real-world and mathematical problems. 7.G.6. Solve real-world and mathematical problems involving area, volume and surface area of two- and three-dimensional objects composed of triangles, quadrilaterals, polygons, cubes, and right prisms. Assessments Provide one assessment item for each content standard (one standard per box). For each assessment include: 1) standard + descriptive title + (Rigor) 2) an actual assessment item or quality description of the assessment 3) connection to Rdg, Wrtg, or Math Practice (if appropriate) 8.G.9 (Apply/DOK 3) A wine glass has a conical shape, and its dimensions are given below. What is the volume of glass necessary to manufacture the wine glass?

07248ea3290173b920ed71ac382e1a02.docx Page 36 1.74 in3 2.66 in3 2.99 in3 4.04 in3

07248ea3290173b920ed71ac382e1a02.docx Page 37 This section completed per whole unit. (Its purpose is to focus on integrating the standards through resources & instructional strategies that focus on unit big ideas.) UNIT Resources & Instruction Primary text connections: List chapters, pages, etc. CJHS- Holt McDougal Course 3 (green)  Chapter 8 o 8-5 Volume of Prisms and Cylinders pg 417 o 8-6 Volume of Pyramids and Cones pg 424

Integration of Technology: Specific examples that apply the technology standards in the content. These links help compare the relationship between different size containers and their volume. Cubed Cans - Exploring Changing from a Cylinder to a Rectangular Prism while Keeping the Volume Constant

Integration of ELP Strategies: (Language, Grammar, etc) Completed by SEI/ELP teachers (later)

07248ea3290173b920ed71ac382e1a02.docx Page 38 Unit 7: Patterns in Data Subject/Course: Pre-Algebra Grade Level: 8th School Year: 2013-2014

Common Core Standards / State Standards Content Standard: Domain: Statistics and Probability including CODE + Cluster: Investigate patterns of association in bivariate data. (Rigor) Standard Code: o 8.SP.1. Construct and interpret scatter plots for bivariate measurement data to investigate patterns of association between two quantities. Describe patterns such as clustering, outliers, positive or negative association, linear association, and nonlinear association. (Analyze/ DOK 3) o 8.SP.2 Know that straight lines are widely used to model relationships between two quantitative variables. For scatter plots that suggest a linear association, informally fit a straight line, and informally assess the model fit by judging the closeness of the data points to the line. o 8.SP.3. Use the equation of a linear model to solve problems in the context of bivariate measurement data, interpreting the slope and intercept. (Analyze/ DOK 3) For example, in a linear model for a biology experiment, interpret a slope of 1.5 cm/hr as meaning that an additional hour of sunlight each day is associated with an additional 1.5 cm in mature plant height. o 8.SP.4. Understand that patterns of association can also be seen in bivariate categorical data by displaying frequencies and relative frequencies in a two-way table. Construct and interpret a two-way table summarizing data on two categorical variables collected from the same subjects. Use relative frequencies calculated for rows or columns to describe possible association between the two variables. For example, collect data from students in your class on whether or not they have a curfew. Integration of College and Career Readiness Anchor Standards for Reading Reading Standard & Craft and Structure(R) 07248ea3290173b920ed71ac382e1a02.docx Page 39 Writing Standard 4. Interpret words and phrases as they are used in a text, and/or Math including determining technical, connotative, and figurative Practice meanings, and analyze how specific word choices shape meaning including CODE or tone. Integration of Knowledge and Ideas(R) Integrate and evaluate content presented in diverse media and formats, including visually and quantitatively, as well as in words College and Career Readiness Anchor Standards for Writing Range of Writing(W) 10.Write routinely over extended time frames (time for research, reflection, and revision) and shorter time frames (a single sitting or a day or two) for a range of tasks, purposes, and audiences. The Mathematical Practices: 1. Make sense of problems and persevere in solving them. 2. Reason abstractly and quantitatively. 3. Construct viable arguments and critique the reasoning of others. 4. Model with mathematics. 5. Use appropriate tools strategically. 6. Attend to precision. 7. Look for and make use of structure. 8. Look for and express regularity in repeated reasoning. Technology ET08-S1C3-01 Standard: Identify patterns and trends to forecast possibilities from different including CODE perspectives. ET08-S1C3-02 Ask questions and investigate a problem from different perspectives and formulate inferences from known facts. ET08-S2C2-01 Communicate and collaborate for the purpose of producing original works or solving problems. ET08-S3C2-04 Synthesize research information to create new understanding. ET08-S6C1-03 Choose technology applications appropriate for the audience and task. ET08-S6C2-03 Apply formatting features while using spreadsheet programs to customize tables, charts, and graphs. ELP Standard: Completed by SEI/ELP teachers (later) including CODE

07248ea3290173b920ed71ac382e1a02.docx Page 40 Clarifications of Content Standard Academic Vocabulary: What academic vocabulary does the student need to know? Scatter Plot, Correlation, Outliers, Line of Best Fit Declarative Knowledge: What concepts (facts, ideas, cause/effect) does the student need to KNOW? Scatter Plots Patterns o Clustering o Outliers o Positive or Negative o Linear o Nonlinear Frequencies Two-way table o variables Equation of Linear Model o Slope and Intercept Line of best fit Procedural Skill: What procedures (steps, algorithms, tactics) does the student need to know HOW to DO?  CONSTRUCT (scatter plots)  INTERPRET (scatter plots)  INVESTIGATE (patterns)  DESCRIBE (patterns)  USE (equation of a linear model)  SOLVE (in context)  INTERPRET (slope and intercept)  UNDERSTAND (patterns of association in data)  DISPLAY (frequencies and relative frequencies)  DESCRIBE (association between variables)  DRAW (line of best fit) Prerequisites: Use Hess’s Cognitive Rigor Matrix to “map” pre-requisite conceptual & procedure knowledge Students must know; 6.SP.1. Recognize a statistical question as one that anticipates variability in the data related to the question and accounts for it in the answers. 6.SP.2. Understand that a set of data collected to answer a statistical question has a distribution which can be described by its center, spread, and overall shape. 8.EE.7. Solve linear equations in one variable. 8.F.4. Construct a function to model a linear relationship between two quantities. Determine the rate of change and initial value of the function from a description of a relationship or from two (x, y) values, including reading these from a table or from a graph. Interpret the rate of change and initial value of a linear function in terms of the situation it models, and in terms of its graph or a table of values. Assessments Provide one assessment item for each content standard (one standard per box). For each 07248ea3290173b920ed71ac382e1a02.docx Page 41 assessment include: 1) standard + descriptive title + (Rigor) 2) an actual assessment item or quality description of the assessment 3) connection to Rdg, Wrtg, or Math Practice (if appropriate) 8.SP.1 (Analyze/DOK 3) The scatter plot in the figure below shows the GPA of the students of a class versus their commute time. Which of the following statements is true?

The relationship between GPA and commute time is moderate positive linear. The relationship between GPA and commute time is moderate negative linear. The scatter plot does not have any outliers.

8.SP.3 (Analyze/DOK 3) The Cody Company ran a study on its sales force and learned that the average number of years of experience for each sales team was in direct relation to annual sales volume. Annual Sales (in thousands) 46 35 51 42 33 50 30 Average Years of Experience 6 4 8 5.5 3 7 2.5 a) Write the Line of Best Fit: y = ______x + ______b) What does the Slope mean in the real world? c) What does the y-intercept mean in the real world? d) Use the Line of Best Fit to predict Annual Sales of a Person with 10 years experience. (Hint: find y) e) How long would someone have to work to earn $80,000

07248ea3290173b920ed71ac382e1a02.docx Page 42 This section completed per whole unit. (Its purpose is to focus on integrating the standards through resources & instructional strategies that focus on unit big ideas.) UNIT Resources & Instruction Primary text connections: List chapters, pages, etc. CJHS- Holt McDougal Course 3 (green)  Chapter 9 o 9-9 Scatterplots pg 504 . Lab Create a Scatter Plot Supplemental Text Connections: List other school-purchased curriculum resources. Other materials available: List other useful resources, teacher-created, online, etc. http://www.free-test-online.com/ccss/grade8/grade8_numbers. http://maccss.ncdpi.wikispaces.net/file/view/CCSSMathTasks-Grade8.pdf http://bsmith.cmswiki.wikispaces.net/file/view/RegressionPractice.pdf Teaching the Common Core Math Standards with Hands on activies Jossey-Bass Teacher Instructional Strategies: Research-based strategies that “fit.”  Grouping students  Questioning techniques  Setting high expectations for all students  Providing visual aids  Varity of assessments  Varity of technology usage Integration of Technology: Specific examples that apply the technology standards in the content. Students will use Shodor Interactive activity to make a scatter plot. Provide students with data that represents a linear relationship. From scatter plot display have students interpret the relationship by determining line of best fit, determine an approximate linear equation, identify the slope. Students work in small groups or in pairs to construct and interpret data by creating two- way tables using Word, Keynote or other program. Have students share their two-way tables with other groups for comparison of group analysis. Teacher can provide data through survey or extend by having students create their own two question survey. Google Drive Survey Monkey

From a scatter plot display have students interpret the relationship by determining line of best fit, determine an approximate linear equation, identify the slope and y-intercept. Scatter Plot

 Students work in small groups or in pairs to construct and interpret data by creating two- way tables using Word, Keynote or other program. (a)Have students share their two-way tables with other groups for comparison of group analysis. (b)Teacher can provide data through survey or extend by having students create their own two question survey using. Collaborative Online Projects Google Drive Survey Monkey 07248ea3290173b920ed71ac382e1a02.docx Page 43 Students will view instructional videos to learn how to create a scatter plot using a spreadsheet program. Then transfer their understanding to make their own scatter plots. YouTube Instructional Video Excel 2010 Scatter Diagram with Trendline - JJMcGrory YouTube Instructional Video How to make a basic scatter plot in Excel 2007 - COCCmath YouTube Instructional Video Scatter Plots in Numbers.mov - nuuploads

Have students create scatter plots using Excel or another spreadsheet program. Teacher guided practice of what to use when data collection [excel, writing (word processing, compare/contrast, diagramming)]. Integration of ELP Strategies: (Language, Grammar, etc) Completed by SEI/ELP teachers (later)

07248ea3290173b920ed71ac382e1a02.docx Page 44