What Is Discrete (Decision) Maths s1

Eulerian and Semi Eulerian Graphs

Envelope Problem

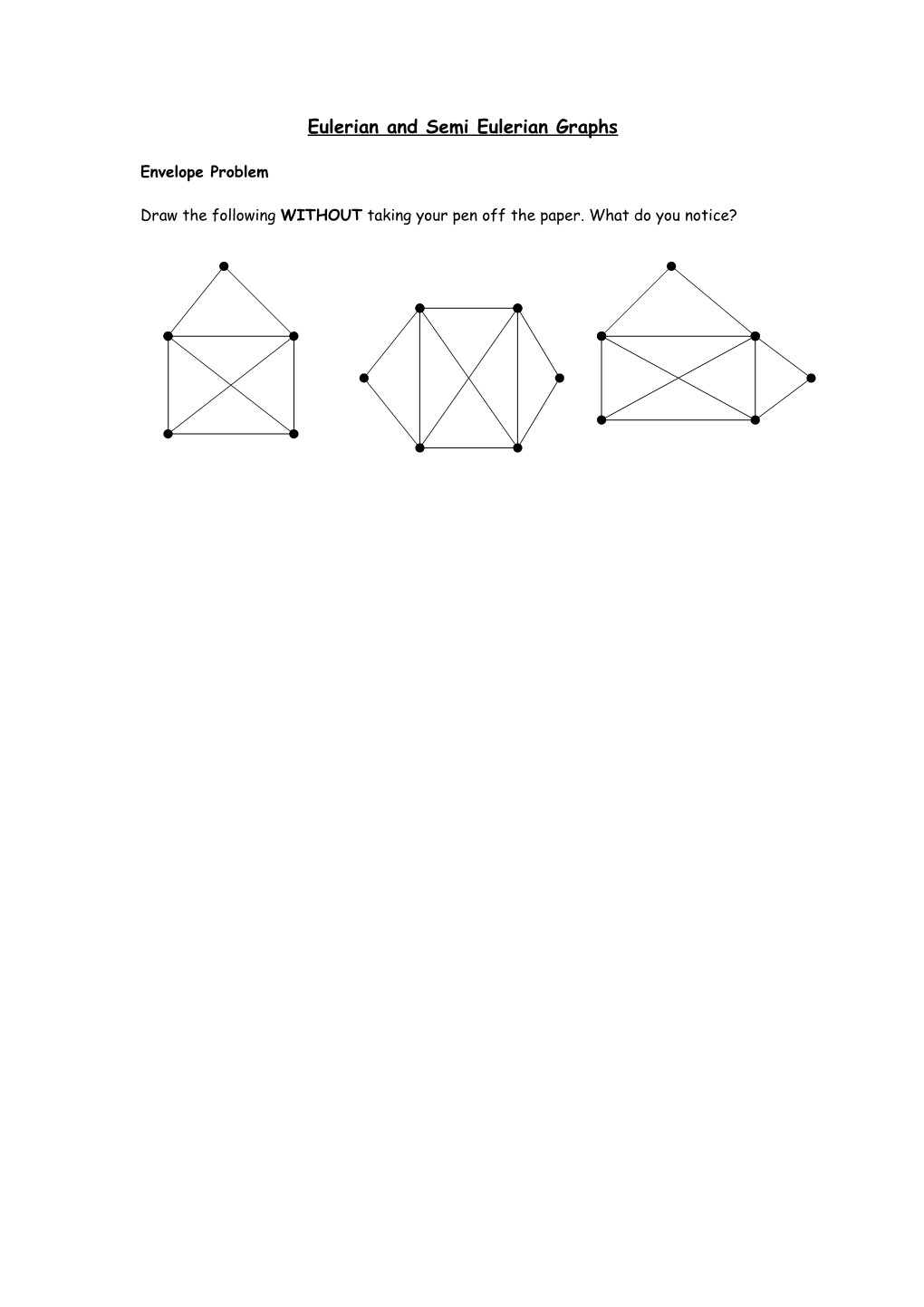
Draw the following WITHOUT taking your pen off the paper. What do you notice? In the first and third diagram two of the nodes have an odd order and you cannot start and finish at the same node. To complete the task without removing your pen from the paper and not going back over an existing edge you need to start at one of the odd nodes and you will then finish at the other odd node.

In the second diagram all nodes have an even order. It is possible to start at any node and, without removing your pen from the paper and not going back over an existing edge, finish at the same node.

Eulerian Graphs A graph is EULERIAN if a CYCLE (start and end at the same point) exists that includes every edge exactly once. This can only happen if all the nodes are of an even order.

AECDEBCA is on Eulerian Cycle.

E C Can you find other?

E.g. Show that the following graph is Eulerian. Describe a possible cycle.

Order A = 4 B = 4 C = 2 As all nodes have an even order then the graph is Eulerian. D = 4 E = 4 F = 4 Possible cycle A B C D B F D E F A E G A G = 2 Semi Eulerian Graphs A graph is said to be SEMI EULERIAN if a TRAIL (no edges appear twice) exists that includes every edge exactly once. This can only happen if EXACTLY two of the nodes have odd order and all the rest have even order.

E B Order A = 2 B = 4 C = 3 D = 3 E = 4

As there are exactly two odd nodes then the graph is Semi Eulerian. The trial must either start at C and end at D or start at D and end at C. D E C B E A B D C is a Semi Eulerian trial.

E.g. Show that the following graph is Semi Eulerian. Describe a possible trial.

Order A = 3 B = 4 C = 2 Graph is Semi Eulerian as only 2 nodes have odd order D = 4 E = 3 Trial is A B C D A F D E B F E. F = 4

P21 Ex 2A