7.1 Oblique Triangles and the Law of Sines

Math 120 Trigonometry Lecture Notes Chapter 7

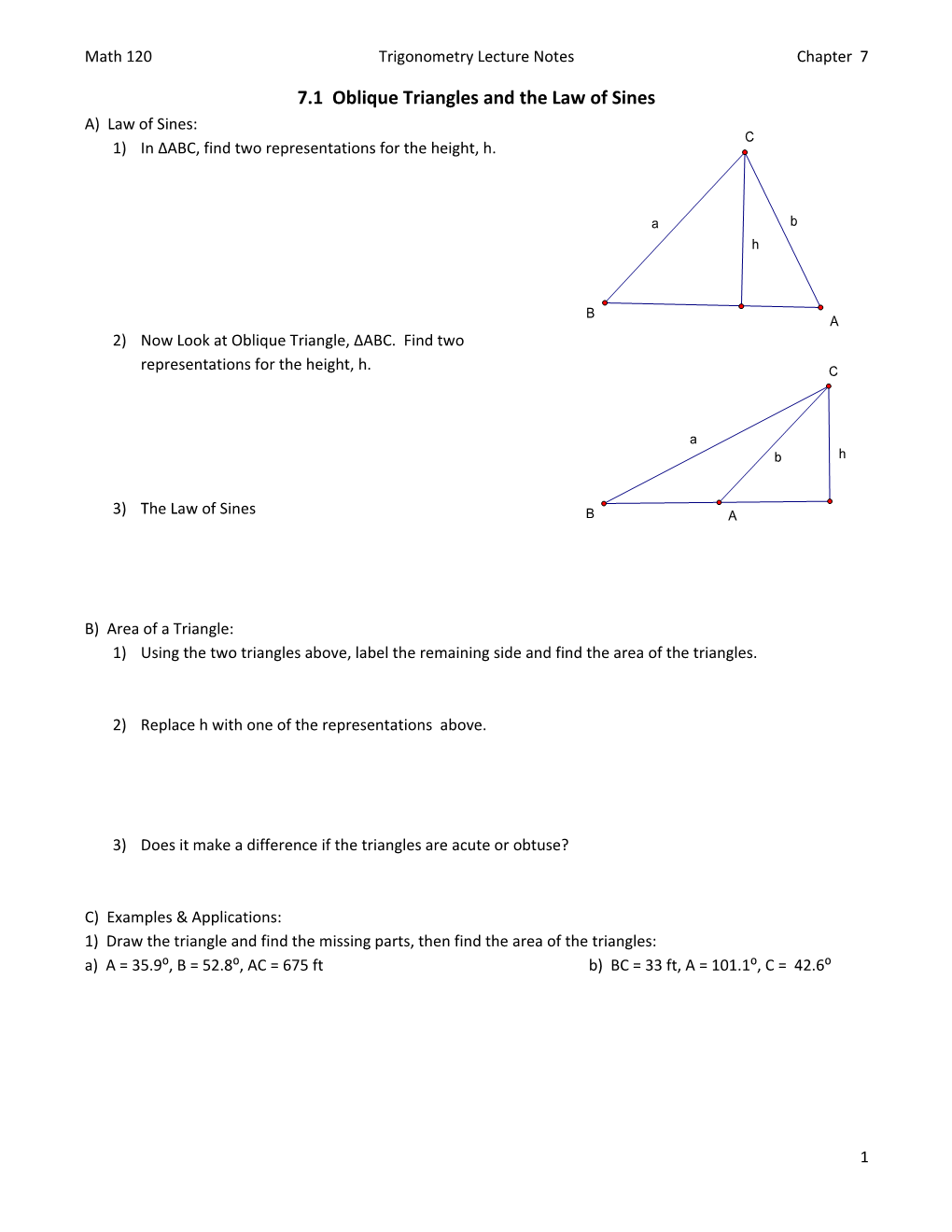
7.1 Oblique Triangles and the Law of Sines A) Law of Sines: C 1) In ∆ABC, find two representations for the height, h.

B A 2) Now Look at Oblique Triangle, ∆ABC. Find two

representations for the height, h. C

3) The Law of Sines B A

B) Area of a Triangle: 1) Using the two triangles above, label the remaining side and find the area of the triangles.

2) Replace h with one of the representations above.

3) Does it make a difference if the triangles are acute or obtuse?

C) Examples & Applications: 1) Draw the triangle and find the missing parts, then find the area of the triangles: a) A = 35.9⁰, B = 52.8⁰, AC = 675 ft b) BC = 33 ft, A = 101.1⁰, C = 42.6⁰

1 Math 120 Trigonometry Lecture Notes Chapter 7

2) A ship notices a lighthouse at bearing N 40.1⁰E. After traveling due north for 3.5 km, the bearing has changed to N 55.2⁰ E. Find the distance from the ship to the lighthouse: a) From it’s original position b) After traveling 3.5 km.

3) A real estate agent wants to find the area of a triangular lot. The surveyor has measured two sides as 16.1 m and 15.2 m. The angle between the two sides is 63.7⁰. Find the area.

7.2 Law of Cosines b A) Triangle Inequality: Sum of any to sides in a triangle must be greater A C than the third side.

B) Law of Cosines: c a c2 = a2 + b2 – 2ab cos C

B  This is true for any side. Variations of Law of Cosines:

 If the triangle is a right triangle, then cos C = ______ Law of Cosines is more accurate than Law of Sines. o If the Cosine is negative, then the angle is ______o If the Cosine is positive, then the angle is ______

o Sine is positive in Quad. ______and ______. o Sin-1 will always give us the angle in Quad ______, but the actual angle may be ______.

C) Heron’ s Formula: Developed by Heron of Alexandria around AD 75 Let s = the semi perimeter (half the perimeter) s =

The Area of a Triangle: A  s(s  a)(s  b)(s  c)

D) Examples & Applications: 1) Find the missing parts of the triangles and use Heron’s formula to find the Area a) A = 41.4⁰, b = 2.78 yd, c = 3.92 yd b) a = 28 ft, b = 47 ft, c = 58 ft

2) A ship is sailing east. At one point, the bearing from the ship to a submerged rock is 45⁰ 20’. After the ship has sailed 15.2 miles, the bearing of the rock is 308⁰ 40’. Find the distance form the ship to the rock at the latter point.

3) Starting at point A, a ship sails 18.5 km at a bearing of 189⁰. It turns and sails 47.8 km at a t bearing of 317⁰. Find the distance of the ship from its starting position, point A.

7.4 Vectors, Operations, & the Dot Product A) Vectors vs. Scalars: 1. Vector Quantities have ______and ______.  Examples of Vectors:

2. Scalar Quantities only have ______.  Examples of Scalars:

3. Vectors are represented by a directed line. The length of the line represents the ______of the vector. The arrow represents the ______.

B) Vector Addition:

18 m 140 N 35⁰ 127⁰ 15 m 225 N

1) To add:  Put vectors head to tail.  Resultant Vector starts at the tail of the first vector and ends at the head of the second vector.  Draw in a parallelogram. The resultant will be the diagonal of the parallelogram.  The angle between the vectors will be the supplement of the angle given.  Use the Law of Sines or Cosines to solve. 2) Vector Subtraction: u – v = u + (-v)  Rotate v 180⁰, which will give you –v. Add that vector to u. 3) Subtract two of the vectors from the previous example.

 C) Component Representation: u  a, b  aiˆ  bˆj a is the magnitude of the component in the x-direction b is the magnitude of the component in the y-direction i is the unit vector in the x-direction j is the unit vector in the y-direction  Vector Addition: o Add the x – components, and add the y – components.  Vector Subtraction: o Subtract the x – components, and subtract the y – components.  Multiplying by a Scalar: o Multiply both components by the scalar.  Opposite of a Vector: o Multiply both components by -1.  To find the Magnitude of the Vector: |u| o Draw the corresponding triangle o Use Pythagorean Thm to find the hypotenuse o The hypotenuse is the magnitude  Direction of the Vector: y  component o tan   x  component o tan-1 will give an angle between ______and ______

o Find the positive angle in the appropriate quadrant. D) Examples: 1) Given vectors: u = 3i + 5j v = -2i – 8j a) Find the other component representation of u and v. b) u + v c) u – v

d) 3u 3) -2v f) Magnitude and direction of u and v.

2) If you are given the magnitude, |u|, & direction, θ, to find the components:  u  a, b a = ______b = ______

3) For a vector with magnitude 36 m/s and direction θ = 245⁰, find the x and y components.

E) Dot Products: 1) Example: Work = Force times displacement (if the two are in the same direction) W = F ∙ d The girl is pulling the wagon with a force of 20 N. The handle makes an angle of 50⁰ with the horizontal. If she pulls the wagon 30m, how much work does she do?

Note: Work is NOT a vector quantity. Image found at: http://identifind.com/safetysake.html 2) Properties of Dot Products:  Dot Products can be found two ways: o u ∙ v = |u| |v| cos θ o For u = a, b and v = c, d , u ∙ v = ac + bd  Dot products are scalars.  They have the following properties: o Commutative: o Associative: o Scalar Multiplication: o 0 ∙ u = o u ∙ u = 3) Given vectors: u = 3i + 5j v = -2i – 8j a) u ∙ v b) v ∙ u c) (3u) ∙ v d) u ∙ (3v)

4) Orthogonal Vectors are at ______angles.  cos ______= ______ What is the dot product of orthogonal vectors?

7.5 Applications of Vectors  Whenever an object is not moving, the sum of the forces acting upon it must be 0. 1) Example: Two forces are acting upon a stationary object. One force is 70 N, and the other is 43 N. The angle between these forces is 75⁰. Since the object is not moving, there must be another force which balances the other two, the ______. Find this force and the angle between it and the 70 N force.

2) Incline Plane: If an object rests on an inclined plane, then an equilibrant force balances the force of gravity. Example: A box that weighs 10 lb is resting on a 25⁰ inclined plane. Find the force required to keep the box from sliding down.

3) Airplanes:  Airspeed is the speed of the plane (without the effects of wind).  Groundspeed is the speed of the plane plus the speed of the wind, taking into account that both are vector quantities, acting at an angle. Ground speed is the vector sum of airspeed + wind speed. a) Example: A plane flies 650 mph on a bearing of 175.3⁰. A 25 mph wind, from a direction of 266.6⁰, blows against the plane. (This means it is coming from a bearing of 266.6⁰. That is the tail of the vector, the wind is headed the opposite direction). Find the resulting bearing and speed of the plane.

b) Example: What bearing and airspeed are required for a plane to fly 400 mi due north in 2.5 hours is the wind is blowing from a direction of 328⁰ at 11 mph?