AP Calculus Problem Set 65
Total Page：16
File Type：pdf, Size：1020Kb
Name______
AP Calculus BC Problem Set 7
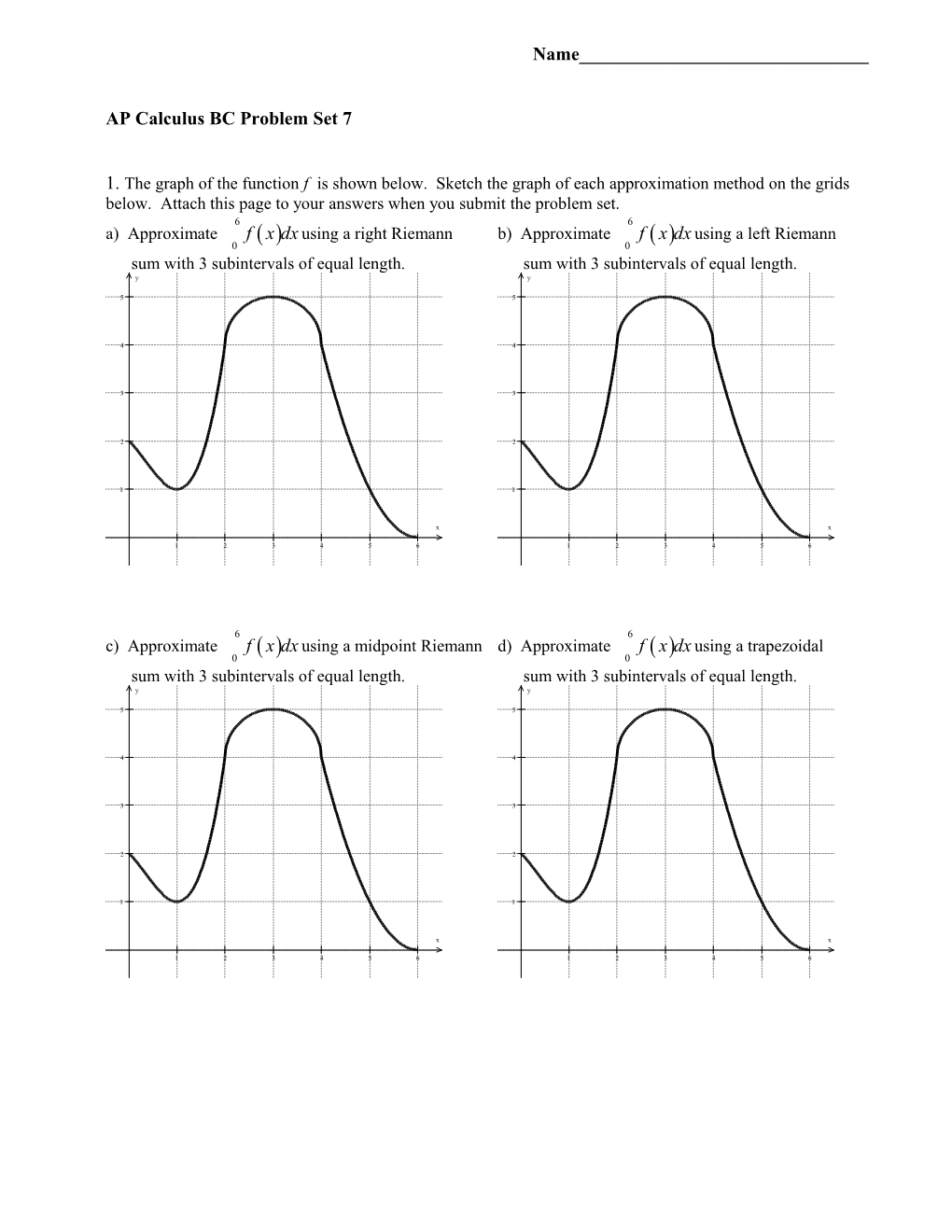
1. The graph of the function f is shown below. Sketch the graph of each approximation method on the grids below. Attach this page to your answers when you submit the problem set. 6 6 a) Approximate f( x) dx using a right Riemann b) Approximate f( x) dx using a left Riemann 0 0 sum with 3 subintervals of equal length. sum with 3 subintervals of equal length. y y
x x
6 6 c) Approximate f( x) dx using a midpoint Riemann d) Approximate f( x) dx using a trapezoidal 0 0 sum with 3 subintervals of equal length. sum with 3 subintervals of equal length. y y
x x
2. A post office delivered letters between 7 a.m. (t = 0) and 5 p.m. (t = 10). The number of letters delivered t hours after noon is modeled by a differentiable function L for 0＃t 10 . Lⅱ( t) > 0 for all t. Values of L( t) , in thousands of letters, at various time t are shown in the table below.
t 0 3 7 8 10 (hours) L( t) 0 1 4 5 9 (thousands of letters) 10 a) Use a trapezoidal sum with the four subintervals given by the table to approximate L( t) dt 0 10 Does this approximation overestimate or underestimate the actual value of L( t) dt ? 0 Give a reason for your answer. 1 10 b) Use a left Riemann sum with the four subintervals given by the table to approximate L( t) dt 10 0 1 10 Using correct units, explain the meaning of L( t) dt , in terms of the number of letters delivered. 10 0
3. During the time interval 0＃t 24 hours, snow accumulates on a driveway at the rate N( t) cubic feet per hour. The table below gives values of N( t) , a strictly monotonic differentiable function, for selected values of t. 24 1 24 a) Using correct units, explain the meaning of N( t) dt and N( t) dt in terms of t N( t) 0 24 0 the snow in the driveway. 0 0 b) Use a midpoint Riemann sum with three subintervals of equal length to 4 12 24 approximate N( t) dt . Show the computations that lead to your answer. 8 20 0 12 25 c) Use a right Riemann sum with three subintervals of equal length to approximate 16 30 1 12 N( t) dt . Show the computations that lead to your answer. Does this 20 50 12 0 24 55 1 12 approximation overapproximate or underapproximate the actual value of N( t) dt 12 0 ? Justify your answer.
4. The velocity of a particle moving along the x-axis is modeled by a differentiable function, v, in meters per second. Selected values of v( t) are given in the table below. t 0 8 10 15 27 47 (seconds) v( t) 2 4 -8 -6 -1 3 (meters per second)
47 a) Using correct units explain the meaning of v( t) dt in the context of this problem. 10 47 b) Use a trapezoidal sum with the three subintervals indicated by the table to approximate v( t) dt 10 47 c) Using correct units explain the meaning of v( t) dt in the context of this problem. Use a right 10 47 Riemann sum with the three subintervals indicated by the table to approximate v( t) dt 10 5. Assuming that f(x) is an always increasing function on [a , b], which would be greater: Rn or Ln?
6. Assuming that f(x) is an always decreasing function on [a , b], which would be greater: Rn or Ln?
7. Consider the function from [0 , 8]. Find T4 and M4. Which one is greater? Show your calculations
8. Consider the function from [0 , 8]. Find T4 and M4. Which one is greater? Show your calculations
9. Notice that is concave up and is concave down. Using your answers from 7 and 8, explain when Tn > Mn and Tn < Mn.
10. Now use your answers from 5 and 6 and 9 to write an inequality involving Rn, Ln, Mn, Tn, and 5 f( x) dx for each of the following. 1
(A) (B) y y
x x
(C) (D)
y y
x x