Differential Equation for Oscillating Beam

Experiment #3 Oscillation

Prelab Differential Equation for Oscillating Beam –Use F = ma = my” •Natural Frequency - page 103   New LabVIEW.VI Acquire Waveforms and graph.vi Control sampling rate Graph FFT

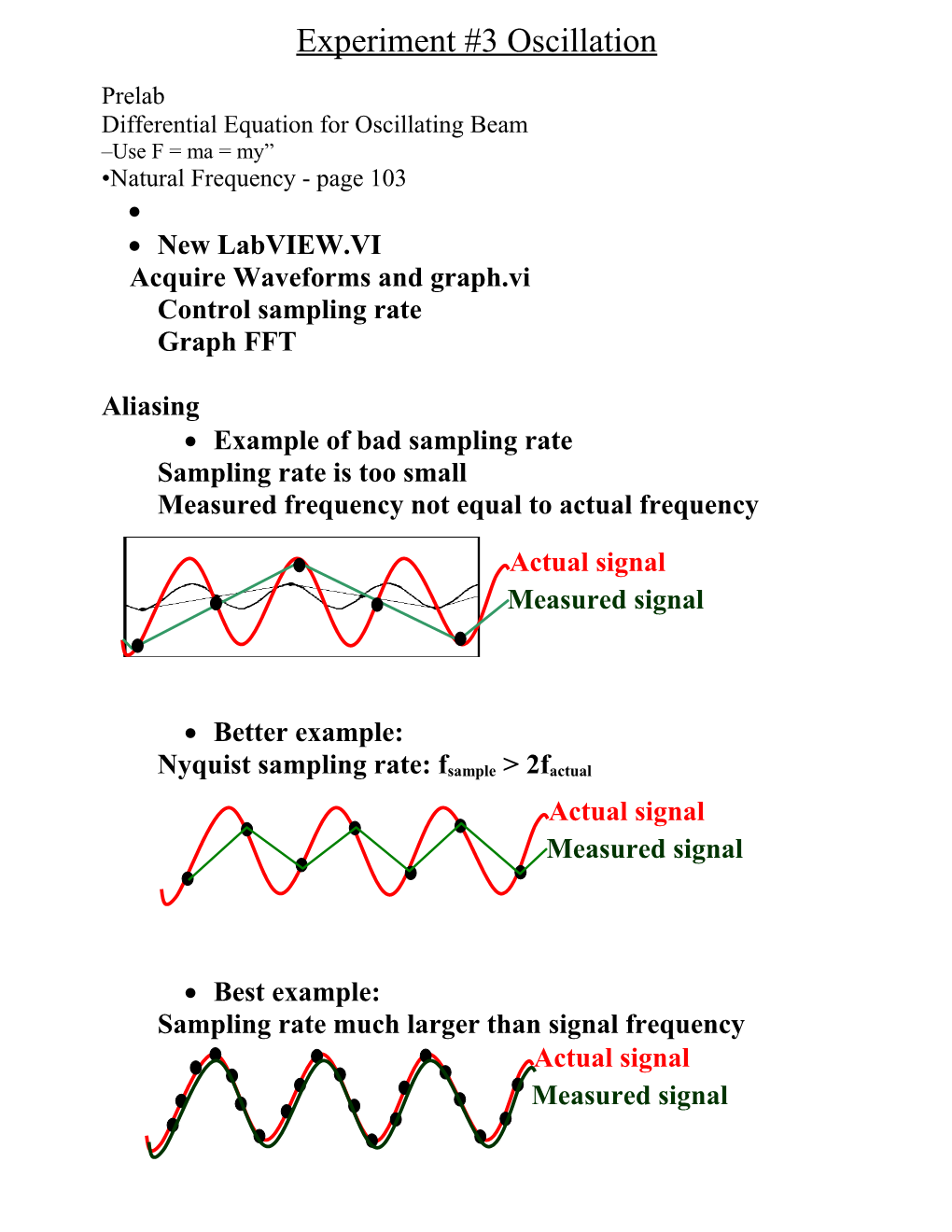
Aliasing  Example of bad sampling rate Sampling rate is too small Measured frequency not equal to actual frequency

Actual signal Measured signal

 Better example:

Nyquist sampling rate: fsample > 2factual Actual signal Measured signal

 Best example: Sampling rate much larger than signal frequency Actual signal Measured signal Good sampling rate:

Sampling rate = ~2* natural frequency Bad sampling rate Resolution: use a low input voltage range, high gain! Resolution of measurement tool

Possible values of tool (i * (vmax-vmin)/(2n - 1) , i (integer) from 0 to (2n –1)

resolution of tool (vmax-vmin)/(2n - 1) , n is # of bits in digital system

T=0 T=1/sampling rate Time (sampling times / rate)

Resolution of measurement tool

Possible values of tool (i * (vmax-vmin)/(2n - 1) , i (integer) from 0 to (2n –1)

resolution of tool (vmax-vmin)/(2n - 1) , n is # of bits in digital system

T=0 T=1/sampling rate Time (sampling times / rate) Questions you need to get done during lab:

#1 – get data for beam with no weight print your LABview window showing the frequency

#4 – Smallest strain from smallest amplitude on graph

#5-#7 Record how amplitudes and frequencies change with weight. (Equations show how amplitudes should change)

#9 - fill in 1st and 3rd column you can fill in the predict f column outside of class

#11 – play around with the sampling rate +V

Blue Green Outside of lab: Fill in explanations: Explain using data you took in class and equations

Note: Clamp beam to the LOWER wooden bench Measure L, w, h, … T C R + R Yellow Do notRed use hugeR -  Ramplitudes Synchronize running LabView, and vibrating beam

C R - R T R + R

Black Expt. 3 Report Corrections & Clarification

Q1) Period (T) = 1/Frequency (f)

Q2) Use the following equation from the back of the beam sheet: Ebh3

 33  3 4 mb Lmax DON’T Mix UNITS Here !!! 140  f  2

You should have the values for E, b, and h from last week’s lab, Expt. 2B. Use a mass of 160 g. for the beam, or you can measure your particular beam for today’s expt. Lmax should be measured from the fixed point to the free end of the cantilever beam. Oh, yes and remember from physics… 2f =  (rad/sec)

English units – make sure you differentiate between mass and force! Here is an example calc: (E = 30e6 * 32ft/s2 * 12in/ft)

english SI E 1.15E+10 2.10E+11 b 0.5 0.0127 h 0.125 0.003175 m 0.345312 0.16 L 17.5 0.4445 f 12.77941 12.77489

Q3) NOTHING TO SEE HERE, MOVE ALONG… Q4) First change “hardware amplifier and DAS” to “software controlled hardware amplifier within DAS” & answer the question. You better know this one… See: PreLab 2B, Q3.

Q5) Accuracy -- how close to the true value are you. No one should talk about accuracy unless you are comparing your values against a standard. We don’t know what the true value is for this expt. However, “accuracy” is a function of the precision of the measuring tool  DAS.

Don’t get the 2 terms confused. I like to equate it to target practice: Accuracy – how close to the bull’s-eye you are. Precision – what your “grouping” of shots looks like  Tight (good precision). Spread out (bad precision)

Q6) First change “weight” to “mass”, and add the phrase “without changing the dimensions, b, h, L (volume)”. Then consider the equation you used for Q2. You can move the 2 to the left side of the eqn. since it’s constant, if that helps you see things more clearly.

Now step back and ponder a small mass versus a large mass oscillating….hmmm. Does your answer make sense?

Q7) First change “weight” to “mass”, and add the phrase “at a specific point in time”. Then look at the wave equations on the beam sheet, specifically the one used for Q10. Again, does your answer make sense? Large mass Vs. Small mass.

Q8) Consider Young’s Modulus (E) of the beam material and the frequency equation used for Q2.

Q9) Once you get the hang of the VI and have checked a few of the frequency values by measuring period in the upper graph. You can let the VI do the work for you & just use the cursors to find the frequency value in the lower graph.

Use the rulers to measure length from fixed point to free end of beam.

Q10) First, change the “b” to a “c”. Then use the following eqn. from beam sheet:  ct / 2m  ct / 2m yt  y e Or, even better… V t  V e m out m

Where, Vm = Max Amplitude, or peak voltage values in your damped signal. e-x is a rapidly decreasing function – Do you see what’s happening?… c = damping coefficient t = time m = mass

Determine damping coefficient (c) using Max Amplitude of oscillation at 3 different time values. Then give answer in terms of a range for “c”. You can do more than 3, if you like.

Make sure 1st point is at the first peak, just after you release the beam. Don’t take data out too far into the damped range V 0  V e 0  V out m m  ct / 2m V t   V e 2 out 2 m  ct / 2m V t   V e 3 out 3 m

1 Vmax Exp curve 0.8

0.6 V(t)

0.4 0.2 t 0 0 0.2 0.4 0.6 0.8 1 1.2 -0.2

-0.8 Q11) Refer to the discussion of “Aliasing” (bottom of pg. 132, Manual) and “Nyquist Theorem” (bottom of pg. 162 Manual) from lecture. And see Jamie’s home page… http://www.mines.edu/fs_home/jmoss/32.doc

Q12) You better know the answer to this one… We talked about it in lecture. It’s trying to ask why this VI versus the Acquire Samples & Chart VI.

Q13) I’ll show you in class…