DOCSLIB.ORG

(Trying To) Solve Higher Order Polynomial Equations. Featuring a Recall of Polynomial Long Division

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text

Load more

(Trying to) solve Higher order polynomial equations. Featuring a recall of polynomial long division. Some history: The quadratic formula (Dating back to antiquity) allows us to solve any quadratic equation. ax2 + bx + c = 0 What about any cubic equation? ax3 + bx2 + cx + d = 0? In the 1540's Cardano produced a \cubic formula." It is too complicated to actually write down here. See today's extra credit. What about any quartic equation? ax4 + bx3 + cx2 + dx + e = 0? A few decades after Cardano, Ferrari produced a \quartic formula" More complicated still than the cubic formula. In the 1820's Galois (age ∼19) proved that there is no general algebraic formula for the solutions to a degree 5 polynomial. In fact there is no purely algebraic way to solve x5 − x − 1 = 0: Galois died in a duel at age 21. This means that, as disheartening as it may feel, we will never get a formulaic solution to a general polynomial equation. The best we can get is tricks that work sometimes. Think of these tricks as analogous to the strategies you use to factor a degree 2 polynomial. Trick 1 If you find one solution, then you can find a factor and reduce to a simpler polynomial equation. Example. 2x2 − x2 − 1 = 0 has x = 1 as a solution. This means that x − 1 MUST divide 2x3 − x2 − 1. Use polynomial long division to write 2x3 − x2 − 1 as (x − 1) · (something). Now find the remaining two roots 1 2 For you: Find all of the solutions to x3 + x2 + x + 1 = 0 given that x = −1 is a solution to this equation. The second trick The Rational roots test. p Imagine that 2x3 + 11x2 − 7x − 6 = 0 had a rational solution . We may as well demand q p that is in reduced terms. q Then: p3 p2 p 2 − 11 − 7 = 6 q3 q2 q Clearing the denominator (by multiplying both sides by q3) gives: Notice that p divides the (left or right)pick one hand side! So p must divide the (left or p right) . But was in reduced terms so p must divide . pick one q List all of the possible p's Now move everything with no q's to the other side of the equation: Now q divides the (left or right)pick one hand side! So q must divide the (left or right)pick one. p But was in reduced terms so q must divide . q List all the possible q's p List all of the possible 's q Are any of them actually roots? 3 Theorem (The rational roots test). If the polynomial equation d d−1 2 adx + ad−1x + ··· + a2x + a1x + a0 = 0 p has a rational solution then p must divide a and q must divide a . q 0 d Use this theorem to find all of the possible rational solutions to 3x3 + 2x + 2 = 0. possible values for p: possible values for q: p possible values for (remember the possible minus sign) q Are any of them actual solutions? Third trick Descartes (The same as the inventor of \Cartesian coordinates" and respon- sible for the epistemological idea of \I think therefore I am") is credited with the following result saying how many solutions should be positive and negative. Theorem (Descartes' Rule of signs). Let d d−1 2 p(x) = adx + ad−1x + ··· + a2x + a1x + a0 be a polynomial (written with the powers of x in descending order.) • The number of positive solutions to p(x) = 0 is equal to either (1) the number of times the sign of the coefficient ak changes OR (2) that same number minus some even integer. • The number of negative solutions to p(x) = 0 is equal to either (1) the number of times d d d d−1 2 the sign of the coefficient of p(−x) = (−1) adx +(−1) ad−1x +···+a2x −a1x+a0 changes OR (2) that same number minus some even integer. example How many positive solutions might p(x) = 4x4 − 2x2 + x + 1 = 0 have? How many negative solutions might p(x) = 4x4 − 2x2 + x + 1 = 0 have? p(−x) = 4 Putting this all together: Try to find the solutions to p(x) = x4−3x3−5x2+13x+6 = 0 Step 1: This is a degree polynomial. What is the greatest that the number of zero's could be? Step 2: Using Descartes Rule of signs, how many positive / negative zero's should there be? Step 3: Use the rational root test to find any possible rational roots. Are any of them actual roots? (split up the work with your groupmates). For each root use polynomial long division (or synthetic division) to pull a linear factor out of the polynomial. REMARK: You might have a root of high multiplicity If you get down to a degree 2 polynomial then use the quadratic formula. 5 Group work: Try to find the solutions to p(x) = x5 − 7x4 + 19x3 − 37x2 + 60x − 36 = 0 Step 1: This is a degree polynomial. What is the greatest that the number of zero's could be? Step 2: Using Descartes Rule of signs, how many positive / negative zero's should there be? Step 3: Use the rational root test to find any possible rational roots. Are any of them actual roots? (split up the work with your groupmates). For each root use polynomial long division (or synthetic division) to pull a linear factor out of the polynomial. REMARK: You might have a root of high multiplicity If you get down to a degree 2 polynomial then use the quadratic formula..
Recommended publications
  • Solving Cubic Polynomials

    Solving Cubic Polynomials

    Solving Cubic Polynomials 1.1 The general solution to the quadratic equation There are four steps to finding the zeroes of a quadratic polynomial. 1. First divide by the leading term, making the polynomial monic. a 2. Then, given x2 + a x + a , substitute x = y − 1 to obtain an equation without the linear term. 1 0 2 (This is the \depressed" equation.) 3. Solve then for y as a square root. (Remember to use both signs of the square root.) a 4. Once this is done, recover x using the fact that x = y − 1 . 2 For example, let's solve 2x2 + 7x − 15 = 0: First, we divide both sides by 2 to create an equation with leading term equal to one: 7 15 x2 + x − = 0: 2 2 a 7 Then replace x by x = y − 1 = y − to obtain: 2 4 169 y2 = 16 Solve for y: 13 13 y = or − 4 4 Then, solving back for x, we have 3 x = or − 5: 2 This method is equivalent to \completing the square" and is the steps taken in developing the much- memorized quadratic formula. For example, if the original equation is our \high school quadratic" ax2 + bx + c = 0 then the first step creates the equation b c x2 + x + = 0: a a b We then write x = y − and obtain, after simplifying, 2a b2 − 4ac y2 − = 0 4a2 so that p b2 − 4ac y = ± 2a and so p b b2 − 4ac x = − ± : 2a 2a 1 The solutions to this quadratic depend heavily on the value of b2 − 4ac.
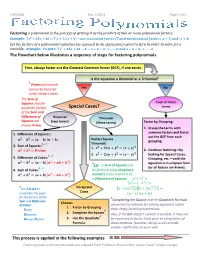
  • Factoring Polynomials

    Factoring Polynomials

    EAP/GWL Rev. 1/2011 Page 1 of 5 Factoring a polynomial is the process of writing it as the product of two or more polynomial factors. Example: — Set the factors of a polynomial equation (as opposed to an expression) equal to zero in order to solve for a variable: Example: To solve ,; , The flowchart below illustrates a sequence of steps for factoring polynomials. First, always factor out the Greatest Common Factor (GCF), if one exists. Is the equation a Binomial or a Trinomial? 1 Prime polynomials cannot be factored Yes No using integers alone. The Sum of Squares and the Four or more quadratic factors Special Cases? terms of the Sum and Difference of Binomial Trinomial Squares are (two terms) (three terms) Factor by Grouping: always Prime. 1. Group the terms with common factors and factor 1. Difference of Squares: out the GCF from each Perfe ct Square grouping. 1 , 3 Trinomial: 2. Sum of Squares: 1. 2. Continue factoring—by looking for Special Cases, 1 , 2 2. 3. Difference of Cubes: Grouping, etc.—until the 3 equation is in simplest form FYI: A Sum of Squares can 1 , 2 (or all factors are Prime). 4. Sum of Cubes: be factored using imaginary numbers if you rewrite it as a Difference of Squares: — 2 Use S.O.A.P to No Special √1 √1 Cases remember the signs for the factors of the 4 Completing the Square and the Quadratic Formula Sum and Difference Choose: of Cubes: are primarily methods for solving equations rather 1. Factor by Grouping than simply factoring expressions.
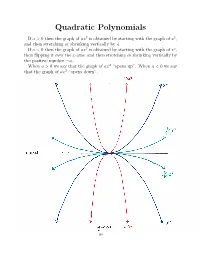
  • Quadratic Polynomials

    Quadratic Polynomials

    Quadratic Polynomials If a>0thenthegraphofax2 is obtained by starting with the graph of x2, and then stretching or shrinking vertically by a. If a<0thenthegraphofax2 is obtained by starting with the graph of x2, then flipping it over the x-axis, and then stretching or shrinking vertically by the positive number a. When a>0wesaythatthegraphof− ax2 “opens up”. When a<0wesay that the graph of ax2 “opens down”. I Cit i-a x-ax~S ~12 *************‘s-aXiS —10.? 148 2 If a, c, d and a = 0, then the graph of a(x + c) 2 + d is obtained by If a, c, d R and a = 0, then the graph of a(x + c)2 + d is obtained by 2 R 6 2 shiftingIf a, c, the d ⇥ graphR and ofaax=⇤ 2 0,horizontally then the graph by c, and of a vertically(x + c) + byd dis. obtained (Remember by shiftingshifting the the⇥ graph graph of of axax⇤ 2 horizontallyhorizontally by by cc,, and and vertically vertically by by dd.. (Remember (Remember thatthatd>d>0meansmovingup,0meansmovingup,d<d<0meansmovingdown,0meansmovingdown,c>c>0meansmoving0meansmoving thatleft,andd>c<0meansmovingup,0meansmovingd<right0meansmovingdown,.) c>0meansmoving leftleft,and,andc<c<0meansmoving0meansmovingrightright.).) 2 If a =0,thegraphofafunctionf(x)=a(x + c) 2+ d is called a parabola. If a =0,thegraphofafunctionf(x)=a(x + c)2 + d is called a parabola. 6 2 TheIf a point=0,thegraphofafunction⇤ ( c, d) 2 is called thefvertex(x)=aof(x the+ c parabola.) + d is called a parabola. The point⇤ ( c, d) R2 is called the vertex of the parabola.
  • The Quadratic Formula You May Recall the Quadratic Formula for Roots of Quadratic Polynomials Ax2 + Bx + C

    The Quadratic Formula You May Recall the Quadratic Formula for Roots of Quadratic Polynomials Ax2 + Bx + C

    For example, when we take the polynomial f (x) = x2 − 3x − 4, we obtain p 3 ± 9 + 16 2 which gives 4 and −1. Some quick terminology 2 I We say that 4 and −1 are roots of the polynomial x − 3x − 4 or solutions to the polynomial equation x2 − 3x − 4 = 0. 2 I We may factor x − 3x − 4 as (x − 4)(x + 1). 2 I If we denote x − 3x − 4 as f (x), we have f (4) = 0 and f (−1) = 0. The quadratic formula You may recall the quadratic formula for roots of quadratic polynomials ax2 + bx + c. It says that the solutions to this polynomial are p −b ± b2 − 4ac : 2a Some quick terminology 2 I We say that 4 and −1 are roots of the polynomial x − 3x − 4 or solutions to the polynomial equation x2 − 3x − 4 = 0. 2 I We may factor x − 3x − 4 as (x − 4)(x + 1). 2 I If we denote x − 3x − 4 as f (x), we have f (4) = 0 and f (−1) = 0. The quadratic formula You may recall the quadratic formula for roots of quadratic polynomials ax2 + bx + c. It says that the solutions to this polynomial are p −b ± b2 − 4ac : 2a For example, when we take the polynomial f (x) = x2 − 3x − 4, we obtain p 3 ± 9 + 16 2 which gives 4 and −1. 2 I We may factor x − 3x − 4 as (x − 4)(x + 1). 2 I If we denote x − 3x − 4 as f (x), we have f (4) = 0 and f (−1) = 0.
  • Positivity Conditions for Cubic, Quartic and Quintic Polynomials Arxiv:2008.10922V10 [Math.GM] 18 Sep 2020

    Positivity Conditions for Cubic, Quartic and Quintic Polynomials Arxiv:2008.10922V10 [Math.GM] 18 Sep 2020

    Positivity Conditions for Cubic, Quartic and Quintic Polynomials Liqun Qi,∗ Yisheng Song,y and Xinzhen Zhang,z August 17, 2021 Abstract We present a necessary and sufficient condition for a cubic polynomial to be positive for all positive reals. We identify the set where the cubic polynomial is nonnegative but not all positive for all positive reals, and explicitly give the points where the cubic polynomial attains zero. We then reformulate a necessary and sufficient condition for a quartic polynomial to be nonnegative for all posi- tive reals. From this, we derive a necessary and sufficient condition for a quartic polynomial to be nonnegative and positive for all reals. Our condition explic- itly exhibits the scope and role of some coefficients, and has strong geometrical meaning. In the interior of the nonnegativity region for all reals, there is an ap- pendix curve. The discriminant is zero at the appendix, and positive in the other part of the interior of the nonnegativity region. By using the Sturm sequences, we present a necessary and sufficient condition for a quintic polynomial to be positive and nonnegative for all positive reals. We show that for polynomials of a fixed even degree higher than or equal to four, if they have no real roots, then their discriminants take the same sign, which depends upon that degree only, except on an appendix set of dimension lower by two, where the discriminants attain zero. arXiv:2008.10922v10 [math.GM] 18 Sep 2020 Key words. Cubic polynomials, quartic polynomials, quintic polynomials, the Sturm theorem, discriminant, appendix. AMS subject classifications.
  • Quartic Equation of General Form

    Quartic Equation of General Form

    EqWorld http://eqworld.ipmnet.ru Exact Solutions > Algebraic Equations and Systems of Algebraic Equations > Algebraic Equations > Quartic Equation of General Form 8. ax4 + bx3 + cx2 + dx + e = 0 (a ≠ 0). Quartic equation of general form. 1±. Reduction to an incomplete equation. The quartic equation in question is reduced to an incom- plete equation y4 + py2 + qy + r = 0.(1) with the change of variable b x = y − 4a 2±. Decartes–Euler solution. The roots of the incomplete equation (1) are given by 1 ¡p p p ¢ 1 ¡p p p ¢ y1 = z1 + z2 + z3 , y2 = z1 − z2 − z3 , 2 2 2 1 ¡ p p p ¢ 1 ¡ p p p ¢ ( ) y3 = 2 − z1 + z2 − z3 , y4 = 2 − z1 − z2 + z3 , where z1, z2, z3 are roots of the cubic equation z3 + 2pz2 + (p2 − 4r)z − q2 = 0,(3) which is called the cubic resolvent of equation (1). The signs of the roots in (2) are chosen so that p p p z1 z2 z3 = −q. The roots of the incomplete quartic equation (1) are determined by the roots of the cubic resolvent (3); see the table below. TABLE Relation between the roots of the incomplete quartic equation and the roots of its cubic resolvent Cubic resolvent (3) Quartic equation (1) All roots are real and positive* Four real roots All roots are real, Two pairs of complex conjugate roots one positive and two negative* One roots is positive Two real and two complex conjugate roots and two roots are complex conjugate 2 * By Vieta’s theorem, the product of the roots z1, z2, z3 is equal to q ≥ 0.
  • Nature of the Discriminant

    Nature of the Discriminant

    Name: ___________________________ Date: ___________ Class Period: _____ Nature of the Discriminant Quadratic − b b 2 − 4ac x = b2 − 4ac Discriminant Formula 2a The discriminant predicts the “nature of the roots of a quadratic equation given that a, b, and c are rational numbers. It tells you the number of real roots/x-intercepts associated with a quadratic function. Value of the Example showing nature of roots of Graph indicating x-intercepts Discriminant b2 – 4ac ax2 + bx + c = 0 for y = ax2 + bx + c POSITIVE Not a perfect x2 – 2x – 7 = 0 2 b – 4ac > 0 square − (−2) (−2)2 − 4(1)(−7) x = 2(1) 2 32 2 4 2 x = = = 1 2 2 2 2 Discriminant: 32 There are two real roots. These roots are irrational. There are two x-intercepts. Perfect square x2 + 6x + 5 = 0 − 6 62 − 4(1)(5) x = 2(1) − 6 16 − 6 4 x = = = −1,−5 2 2 Discriminant: 16 There are two real roots. These roots are rational. There are two x-intercepts. ZERO b2 – 4ac = 0 x2 – 2x + 1 = 0 − (−2) (−2)2 − 4(1)(1) x = 2(1) 2 0 2 x = = = 1 2 2 Discriminant: 0 There is one real root (with a multiplicity of 2). This root is rational. There is one x-intercept. NEGATIVE b2 – 4ac < 0 x2 – 3x + 10 = 0 − (−3) (−3)2 − 4(1)(10) x = 2(1) 3 − 31 3 31 x = = i 2 2 2 Discriminant: -31 There are two complex/imaginary roots. There are no x-intercepts. Quadratic Formula and Discriminant Practice 1.
  • Formula Sheet 1 Factoring Formulas 2 Exponentiation Rules

    Formula Sheet 1 Factoring Formulas 2 Exponentiation Rules

    Formula Sheet 1 Factoring Formulas For any real numbers a and b, (a + b)2 = a2 + 2ab + b2 Square of a Sum (a − b)2 = a2 − 2ab + b2 Square of a Difference a2 − b2 = (a − b)(a + b) Difference of Squares a3 − b3 = (a − b)(a2 + ab + b2) Difference of Cubes a3 + b3 = (a + b)(a2 − ab + b2) Sum of Cubes 2 Exponentiation Rules p r For any real numbers a and b, and any rational numbers and , q s ap=qar=s = ap=q+r=s Product Rule ps+qr = a qs ap=q = ap=q−r=s Quotient Rule ar=s ps−qr = a qs (ap=q)r=s = apr=qs Power of a Power Rule (ab)p=q = ap=qbp=q Power of a Product Rule ap=q ap=q = Power of a Quotient Rule b bp=q a0 = 1 Zero Exponent 1 a−p=q = Negative Exponents ap=q 1 = ap=q Negative Exponents a−p=q Remember, there are different notations: p q a = a1=q p q ap = ap=q = (a1=q)p 1 3 Quadratic Formula Finally, the quadratic formula: if a, b and c are real numbers, then the quadratic polynomial equation ax2 + bx + c = 0 (3.1) has (either one or two) solutions p −b ± b2 − 4ac x = (3.2) 2a 4 Points and Lines Given two points in the plane, P = (x1; y1);Q = (x2; y2) you can obtain the following information: p 2 2 1. The distance between them, d(P; Q) = (x2 − x1) + (y2 − y1) . x + x y + y 2.
  • Low-Degree Polynomial Roots

    Low-Degree Polynomial Roots

    Low-Degree Polynomial Roots David Eberly, Geometric Tools, Redmond WA 98052 https://www.geometrictools.com/ This work is licensed under the Creative Commons Attribution 4.0 International License. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/ or send a letter to Creative Commons, PO Box 1866, Mountain View, CA 94042, USA. Created: July 15, 1999 Last Modified: September 10, 2019 Contents 1 Introduction 3 2 Discriminants 3 3 Preprocessing the Polynomials5 4 Quadratic Polynomials 6 4.1 A Floating-Point Implementation..................................6 4.2 A Mixed-Type Implementation...................................7 5 Cubic Polynomials 8 5.1 Real Roots of Multiplicity Larger Than One............................8 5.2 One Simple Real Root........................................9 5.3 Three Simple Real Roots......................................9 5.4 A Mixed-Type Implementation................................... 10 6 Quartic Polynomials 12 6.1 Processing the Root Zero...................................... 14 6.2 The Biquadratic Case........................................ 14 6.3 Multiplicity Vector (3; 1; 0; 0).................................... 15 6.4 Multiplicity Vector (2; 2; 0; 0).................................... 15 6.5 Multiplicity Vector (2; 1; 1; 0).................................... 15 6.6 Multiplicity Vector (1; 1; 1; 1).................................... 16 1 6.7 A Mixed-Type Implementation................................... 17 2 1 Introduction Consider a polynomial of degree d of the form d X i p(y) = piy (1) i=0 where the pi are real numbers and where pd 6= 0. A root of the polynomial is a number r, real or non-real (complex-valued with nonzero imaginary part) such that p(r) = 0. The polynomial can be factored as p(y) = (y − r)mf(y), where m is a positive integer and f(r) 6= 0.
  • Calculus Method of Solving Quadratic Equations

    Calculus Method of Solving Quadratic Equations

    International Journal of Mathematics Research. ISSN 0976-5840 Volume 9, Number 2 (2017), pp. 155-159 © International Research Publication House http://www.irphouse.com Calculus Method of Solving Quadratic Equations Debjyoti Biswadev Sengupta#1 Smt. Sulochanadevi Singhania School, Jekegram, Thane(W), Maharashtra-400606, India. Abstract This paper introduces a new application of differential calculus and integral calculus to solve various forms of quadratic equations. Keywords: quadratic equations, differential calculus, integral calculus, infinitesimal integral calculus, constant of infinity. I. INTRODUCTION This paper is based on the usage of the principles of differential calculus and integral calculus to solve quadratic equations. It is hypothesized that if we use calculus to solve quadratic equations, we will arrive at the same solution that we may get from the quadratic formula method. It is also hypothesized that the quadratic formula can be derived from the quadratic formula. The paper involves the use of differential and integral calculus which takes solving of quadratic equations to the next level. The formulas which we will come across the paper, or use them, are shown in Table 1 under Heading IV. The paper shall be dealt under 2 headings. Heading II will deal with the use of differential calculus in solving quadratic equations while Heading III will deal with the use of integral calculus in quadratic equations, as far as solving of quadratic equations is concerned. Heading V is hugely concerned about the advantages of using calculus to solve quadratic equation. 156 Debjyoti Biswadev Sengupta II. USE OF DIFFERENTIAL CALCULUS TO SOLVE QUADRATIC EQUATIONS To solve quadratic equations, we shall require the use of first order differential calculus only.
  • IVC Factsheet Quadratics

    IVC Factsheet Quadratics

    Imperial Valley College Math Lab QUADRATICS SUMMARY SHEET (EQUATIONS, FUNCTIONS, AND GRAPHS) The two basic forms of quadratic equations are: 푦 = 푎푥2 + 푏푥 + 푐 푦 = 푎(푥 − ℎ)2 + 푘 The two basic forms of quadratic functions are: 푓(푥) = 푎푥2 + 푏푥 + 푐 푓(푥) = 푎(푥 − ℎ)2 + 푘 SQUARE ROOT PROPERTY If 푋2 = 푘 , then 푋 = ±√푘 . [ can be any algebraic expression, and 푘 is any real number]. Ex: (푥 − 4)2 = 5 → 푥 − 4 = ±√5 → 푥 = 4 ± √5 QUADRATIC FORMULA −푏 ± √푏2−4푎푐 If 푎푥2 + 푏푥 + 푐 = 0 , then 푥 = . 2푎 Remark: Notice that the equation must be set equal to zero first! 2 Ex: 4푥 + 5푥 − 3 = 0 First note that 푎 = 4 , 푏 = 5, and 푐 = −3 . −5 ± √52−4(4)(−3) −5 ± √25−(−48) −5 ± √73 Substitute carefully: 푥 = = = . 2(4) 8 8 Watch the signs! Especially when a or c is negative. THE DISCRIMINANT The type of solution to a quadratic equation depends upon what happens under the radical sign (√ ) . Therefore, if you look at the Quadratic Formula above, you’ll see that the “푏2 − 4푎푐 ” part is important. Definition: For the quadratic equation 푎푥2 + 푏푥 + 푐 = 0 , the discriminant is 푏2 − 4푎푐 . If 푏2 − 4푎푐 > 0 and is a perfect square, then 푎푥2 + 푏푥 + 푐 = 0 has two rational solutions. If 푏2 − 4푎푐 > 0 but is not a perfect square, then 푎푥2 + 푏푥 + 푐 = 0 has two irrational solutions. If 푏2 − 4푎푐 = 0 , then 푎푥2 + 푏푥 + 푐 = 0 has one rational solution. If 푏2 − 4푎푐 < 0 , then 푎푥2 + 푏푥 + 푐 = 0 has two complex solutions (involving the imaginary number ).
  • The Conditions for Multiple Roots in Cubic and Quartic Equations

    The Conditions for Multiple Roots in Cubic and Quartic Equations

    Fort Hays State University FHSU Scholars Repository Master's Theses Graduate School Summer 1953 The Conditions For Multiple Roots In Cubic and Quartic Equations Laurence Dryden Fort Hays Kansas State College Follow this and additional works at: https://scholars.fhsu.edu/theses Part of the Algebraic Geometry Commons Recommended Citation Dryden, Laurence, "The Conditions For Multiple Roots In Cubic and Quartic Equations" (1953). Master's Theses. 508. https://scholars.fhsu.edu/theses/508 This Thesis is brought to you for free and open access by the Graduate School at FHSU Scholars Repository. It has been accepted for inclusion in Master's Theses by an authorized administrator of FHSU Scholars Repository. THE CONDITIONS FOR MULTIPLE ROOTS IN CUBI C AND QUARTIC EQUATIONS being A Thesis Presented to the Graduate F aculty of the Fort Hays Kansas State College in Partial Fulfillment of the Requireme nts for t h e De gree Master of Science by Laurence A. Dryden, B.S. in Education Ohio State University Approved~,R;I;_#~ Major Departme Date 7- '-?.. - ..,-.3 ACKNOWLEDGlvIENT The writer of this thesis wishes to acknowledge all sources of information used in its preparation and is especially indebted to the Head of the Mathematics Department, Professor Emmet C. Stopher, for his assistance, criticisms, and advice. \ TABLE OF CONTENTS CHAPTER PAGE INTRODUCTION 1 I. DISCRil'HNANT 1. Definition of Discriminant ••• . 2 2. Definition of Resultant 2 3. Relation between Discriminant and Resultant 3 4. Definition of Sylvester's Determinant D(f,g) •••• 3 S. Relation between Sylvester's Determinant and Resultant 6. Relation between Discriminant and Sylvester's Determinant 7 7.