Finding Probabilities for the Normal Distribution When the Distribution Is Not Standardized

251distrex3 1/19/07 (Open this document in 'Page Layout' view!)

Finding Probabilities for the Normal Distribution when the Distribution is not Standardized

We already know from the previous section (251disrtex2) that any probability for a Normally distributed variable (the standard notation to say that a given distribution is Normal with a certain mean and standard deviation is ~ N,  ) can be found using the Standardized Normal distribution by using the x   transformation z  .  This means that if x ~ N50,100 and we want P200  x  250 , we replace values of x  50 x with z  . We thus say: 100 200  50 250  50 P200  x  250  P  z    P1.50  z  2.00  100 100 

Since there is no particular reason to repeat the e. P2.00  x  35.00 problems from class, here are some that I had f. P0  x  1.00 available that seem to cover all the bases. Assume that x ~ N(2,9) . Do the following: g. P 3.00  x  1.00 a. P0.50  x  4.00 h. Find probabilities for the following intervals: Below -3.4, 3.4  x  0.7, 0.7  x  2.0 , b. P0.41  x  0.41 2.0  x  4.7, 4.7  x  7.4 and above 7.4. c. F0.24  Px  0.24 (Cumulative) Make diagrams. d. F3.00  Px  3.00

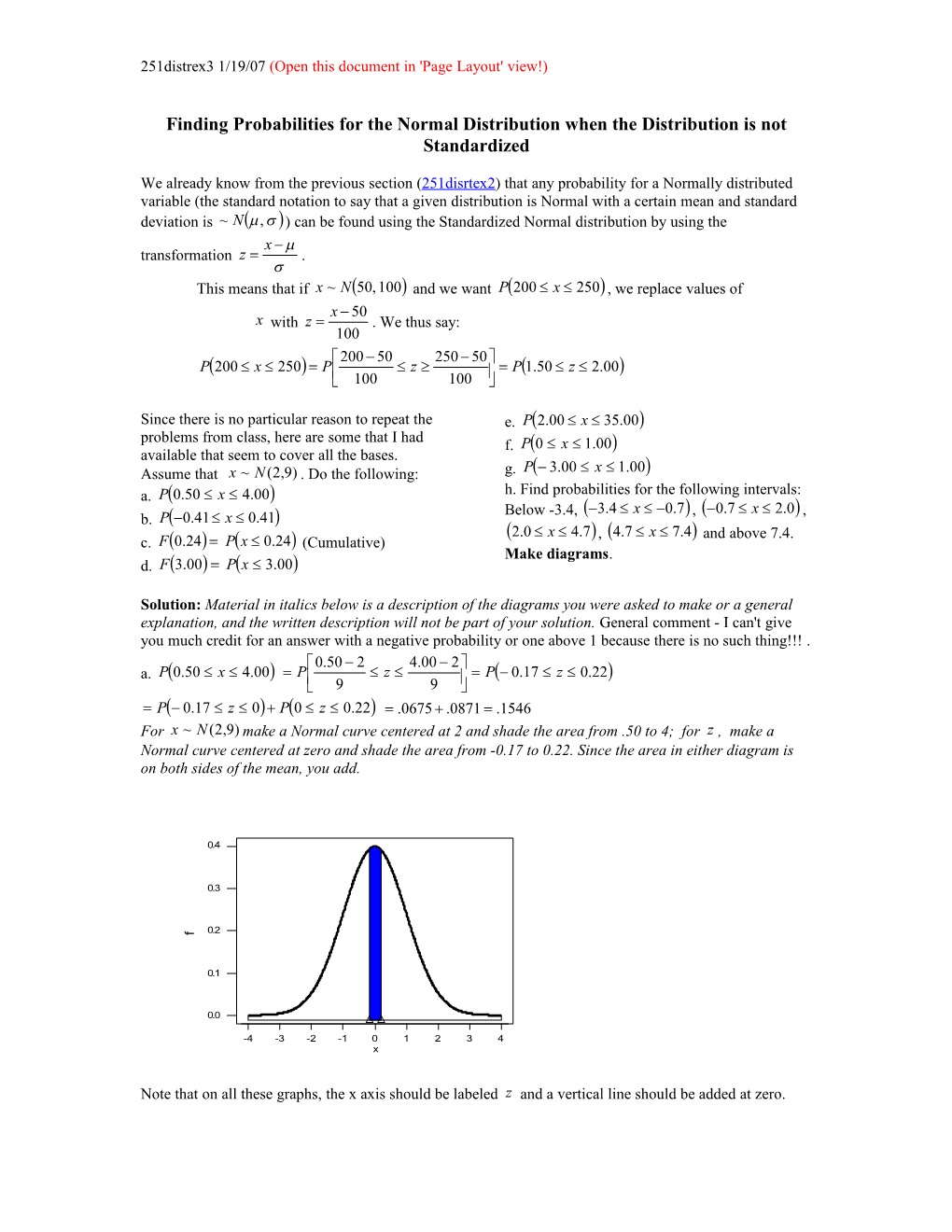
Solution: Material in italics below is a description of the diagrams you were asked to make or a general explanation, and the written description will not be part of your solution. General comment - I can't give you much credit for an answer with a negative probability or one above 1 because there is no such thing!!! . 0.50  2 4.00  2 a. P0.50  x  4.00  P  z    P 0.17  z  0.22  9 9   P 0.17  z  0 P0  z  0.22  .0675  .0871  .1546 For x ~ N(2,9) make a Normal curve centered at 2 and shade the area from .50 to 4; for z , make a Normal curve centered at zero and shade the area from -0.17 to 0.22. Since the area in either diagram is on both sides of the mean, you add.

-4 -3 -2 -1 0 1 2 3 4 x

Note that on all these graphs, the x axis should be labeled z and a vertical line should be added at zero. 251distrex3 1/19/07 (Open this document in 'Page Layout' view!)

 0.41 2 0.41 2 b. P0.41  x  0.41  P  z    P 0.27  z  0.18  9 9   P0.27  z  0 P0.18  z  0  .1064 .0714  .0350

In this problem many students made diagrams showing, correctly, a mean of 2, but then showing 0.41 above it. Also, I got many probabilities like P0  z  0.20 , which don't make any sense because -0.20 is below zero and this says that it is above zero. For x ~ N(2,9) make a Normal curve centered at 2 and shade the area from -0.41 to 0.41; for z make a Normal curve centered at zero and shade the area from – 0.27 to -0.18. Since the area in either diagram is on one side of the mean, you subtract. Like all diagrams in these examples, the diagram below is for z, since most students prefer to make z diagrams rather than x diagrams. A z diagram is always centered at zero. An x diagram is always centered at the population mean (2 in this case).Students who did this problem either (a) assumed that if -0.41 became -0.27, then +0.41 would become +0.27 or (b) didn’t get control of their calculators and got +0.41 – 2 for their first calculation. Doing 0 – 0.41 – 2 might help.

-4 -3 -2 -1 0 1 2 3 4 x 251distrex3 1/19/07 (Open this document in 'Page Layout' view!)

 0.24  2 c. F0.24  Px  0.24  Pz    Pz  0.20  Pz  0 P0.20  z  0  9   .5000 .0793  .4207 . This is the Cumulative distribution. (  is a notation for ‘equal by definition’) We already know from the previous section (251disrtex2) that since the zero is the halfway point under the curve, Pz  0  .5 and Pz  0  .5 . For x ~ N(2,9) make a Normal curve centered at 2 and shade the area below 0.24; for z make a Normal curve centered at zero and shade the area below -0.20. Since the area in either diagram is on one side of the mean, you subtract.

Moral: For a cumulative distribution Fx0   Px  x0  when x0 is below the mean, change x0 to z0 , and subtract P0  z  z0  (from the standardized normal table) from 0.5.

-4 -3 -2 -1 0 1 2 3 4 x . 251distrex3 1/19/07 (Open this document in 'Page Layout' view!)

 3.00  2 d. F3.00  Px  3.00  Pz    Pz  0.11  Pz  0  P0  z  0.11  9   .5000  .0438  .5438 This is the Cumulative distribution. (  is a notation for ‘equal by definition’) For x ~ N (2,9) make a Normal curve centered at 2 and shade the entire area below 3.00; for z , make a Normal curve centered at zero and shade the area below 0.11. Since the area in either diagram is on both sides of the mean, you add.

Moral: For a cumulative distribution Fx0   Px  x0  when x0 is above the mean, change x0 to z0 , and add P0  z  z0  (from the standardized normal table) to 0.5.

2.00  2 35  2 e. P2.00  x  35.00  P  z    P0  z  3.67  P0  z  3.67  .4999  9 9  There are two surprises in this problem. First 3.67 is not on the usual standardized table and, second, one value of z is zero. For x ~ N(2,9) make a Normal curve centered at 2 and shade the area above 2.0; for z , make a Normal curve centered at zero and shade the area above 0. Since the area in either diagram starts at the mean, you imply look up P0  z  3.67 .This would also work for something like P0.50  x  2.00 . To find 3.67, if you have my table, look at the bottom of the table. It is reproduced below. Since 3.67 is between 3.62 and 3.89, we say  P0  z  3.67  .4999 . If you don’t have my table and you know that probabilities between zero and any number above 4 are .5000 and that the conventional table will tell you that P0  x  3.09  .4990 , you can usually make a pretty good guess.

For values above 3.09, see below

If z0 is between P0  z  z0  is

3.08 and 3.10 .4990 3.11 and 3.13 .4991 3.14 and 3.17 .4992 3.18 and 3.21 .4993 3.22 and 3.26 .4994 3.27 and 3.32 .4995 3.33 and 3.38 .4996 3.39 and 3.48 .4997 3.49 and 3.61 .4998 3.62 and 3.89 .4999 3.90 and up .5000

0  2 1  2 f. P0  x  1.00  P  z    P 0.22  z  0.11  P 0.22  z  0  P 0.11  z  0  9 9   .0871  .0438  .0433 Students who did this problem often failed to change zero to -0.22. For x ~ N(2,9) make a Normal curve centered at 2 and shade the area from 0 to 1.00; for z , make a Normal curve centered at zero and shade the area from -0.22 to 0.11. Since the area in either diagram is on both sides of the mean, you subtract.

-4 -3 -2 -1 0 1 2 3 4 x

 3.00  2 1.00  2 g. P 3.00  x  1.00  P  z    P 0.56  z  0.11  9 9   P 0.56  z  0  P 0.11 z  0  .2123 .0438  .1685

-4 -3 -2 -1 0 1 2 3 4 x 251distrex3 1/19/07 (Open this document in 'Page Layout' view!) h. Find probabilities for the following intervals: Below -3.4,  3.4  x  0.7 , 0.7  x  2.0 , 2.0  x  4.7, 4.7  x  7.4 and above 7.4.

This type of problem is a preface to a procedure commonly used in Economics 252 called the Kolmogorov – Smirnov test or the Chi-squared test, or, in the case with the Normal distribution where x and s are known rather than  and  and are used in their place, the Lilliefors test. They are based on the fact that the sums of the differences squared between the proportion of points on intervals in a hypothesized distribution and the proportion of the points on the same interval in a sample from the actual distribution have a well known distribution. To start, we divide the hypothesized distribution into intervals and figure out their probabilities. You can, of course, do each of these separately, but a mass production technique based on the cumulative distribution is somewhat faster, though I am waiting for one of my students to invent one that is more efficient. The way this is done is that you take your values of x ~ N(2,9) above in x  2 your first column, convert them to z  in the second column, compute Fz as in c.) and d.) above 9 in the third column, and difference the third column into the 4th column by subtracting each number in the column except the first one from the number above it. For x ~ N(2,9) make a Normal curve centered at 2 and shade the areas below-3.4, from -3.4 to -0.07, -0.07 to 2.0, 2.0 to 4.7, 4.7 to 7.4 and above 7.4; for z make a Normal curve centered at zero and shade the areas below -0.6, between -0.6 and -0.3 etc. In either case, you will notice that the areas that you marked off are symmetrical about the mean, which means that the probabilities above the mean are unnecessary.

Row x z Fz Probability 1 -3.4 -0.6 .5 - .2257 = .2743 .2743 = .2743 2 -0.7 -0.3 .5 - .1179 = .3821 .3821 - .2743 = .1078 3 2.0 0.0 .5 = .5000 .5000 - .3821 = .1179 4 4.7 0.3 .5 + .1179 = .6179 .6179 - .5000 = .1179 5 7.4 0.6 .5 + .2257 = .7757 .7757 - .6179 = .1078 6   1 = 1.0000 1.0000 - .7757 = .2743

So Px  3.4  F3.4  .2743 , P3.4  x  0.7  .1078 , P0.7  x  2.0  .1179 , P2.0  x  4.7  P0.7  x  2.0  .1179 , P4.7  x  7.4  P3.4  x  0.7  .1078 and Px  7.4  1 F7.4  Px  3.4  F3.4  .2743 .