Classwork/ Guided Practice on Integers

Study Guide: Adding Integers

Adding Integers: Using a number line:

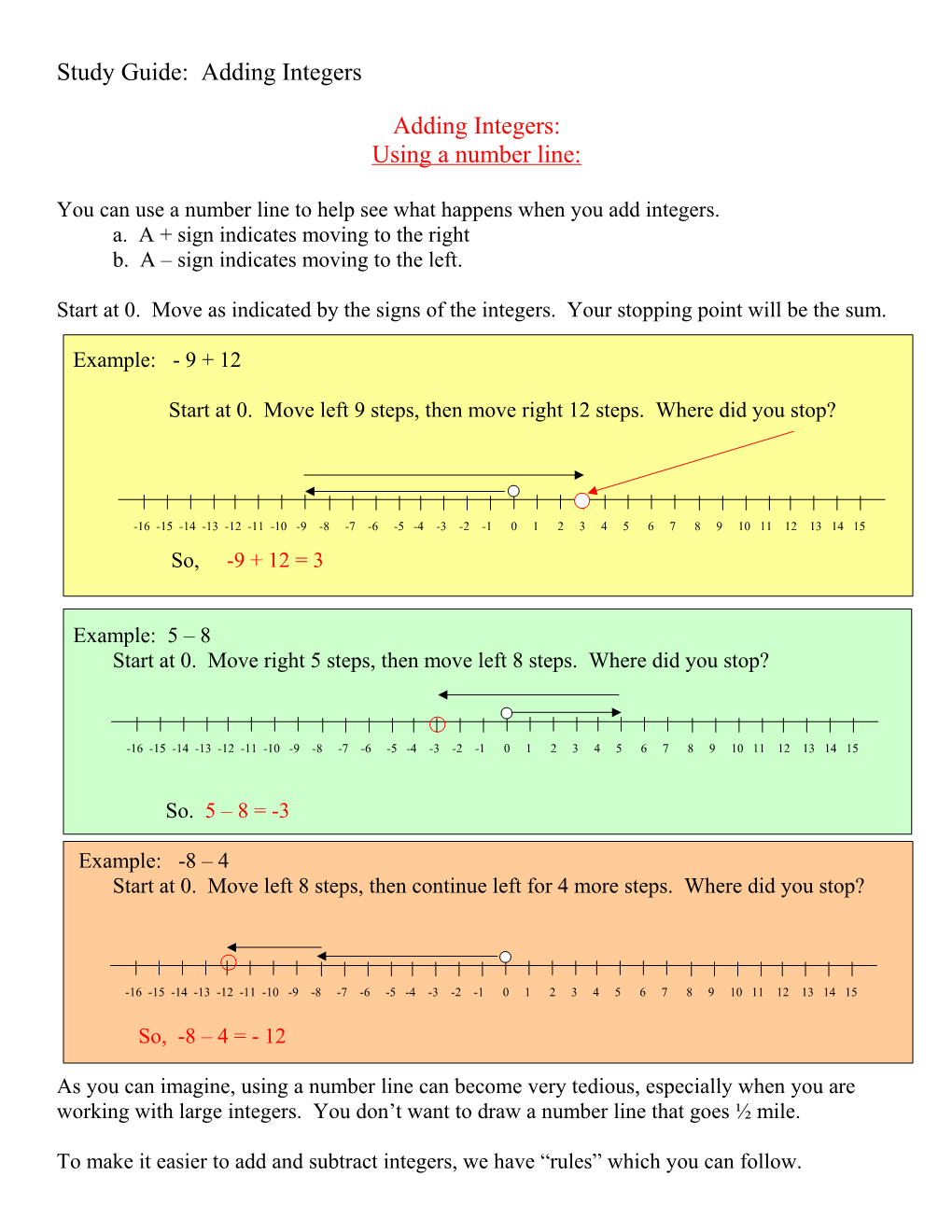
You can use a number line to help see what happens when you add integers. a. A + sign indicates moving to the right b. A – sign indicates moving to the left.

Start at 0. Move as indicated by the signs of the integers. Your stopping point will be the sum.

Example: - 9 + 12

Start at 0. Move left 9 steps, then move right 12 steps. Where did you stop?

-16 -15 -14 -13 -12 -11 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 So, -9 + 12 = 3

Example: 5 – 8 Start at 0. Move right 5 steps, then move left 8 steps. Where did you stop?

-16 -15 -14 -13 -12 -11 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

So. 5 – 8 = -3

Example: -8 – 4 Start at 0. Move left 8 steps, then continue left for 4 more steps. Where did you stop?

-16 -15 -14 -13 -12 -11 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

So, -8 – 4 = - 12

As you can imagine, using a number line can become very tedious, especially when you are working with large integers. You don’t want to draw a number line that goes ½ mile.

To make it easier to add and subtract integers, we have “rules” which you can follow. Adding Integers: Using Rules:

1. To add two integers with the same sign, add their absolute values and keep the sign.

Examples: 7 + 4 = 11 Both of these integers are positive. - 8 + (-6) = -14 Both of these integers are negative.

*** If the problem is written as -6 – 7, consider the sign in front of the integer as the sign of that integer. In this case, we have a negative 6 and a negative 7. They have the same sign. Then using the rule above, – 6 – 7 = – 13

2. To add two integers with different signs, subtract their absolute values and take the sign of the number with the larger absolute value. (The one farther from 0.)

Examples: 9 + (-4) = 5 Absolute values are 9 and 4, the difference is 5. 9 has the larger absolute value and is positive, so the answer will be positive.

-12 + 8 = – 4 Absolute values are 12 and 8, the difference is 4. -12 has the larger absolute value and is negative, so the answer will be negative.

3. To subtract two integers, be sure to have only one sign between the integers. Then use the addition rules. a. If you are subtracting a positive integer, change the middle sign to – . 8 – (+ 5) : change this to 8 – 5 ( a + and – together make a – )

b. If you are subtracting a negative integer, change the middle sign to +. 8 – ( – 5 ) : change this to 8 + 5 (a – and – together make a +)

Examples: 1. 5 – 9 = – 4 (different signs, subtract) 2. – 6 + 10 = 4 (different signs)

3. 7 – ( – 2 ) = 7 + 2 = 9 (same signs, add) 4. – 5 – 6 = - 11 (same signs)

5. – 8 + 6 = – 2 (different signs) 6. – 9 – (+6) = – 9 – 6 = -15 (same signs)

7. 4 + 10 = 14 (same signs) 8. 7 – 3 = 4 (different signs)

9. – 5 – (– 3 ) = – 5 + 3 = – 2 (different signs) 10. – 4 – 13 = – 17 (same signs)