The Airport Problem

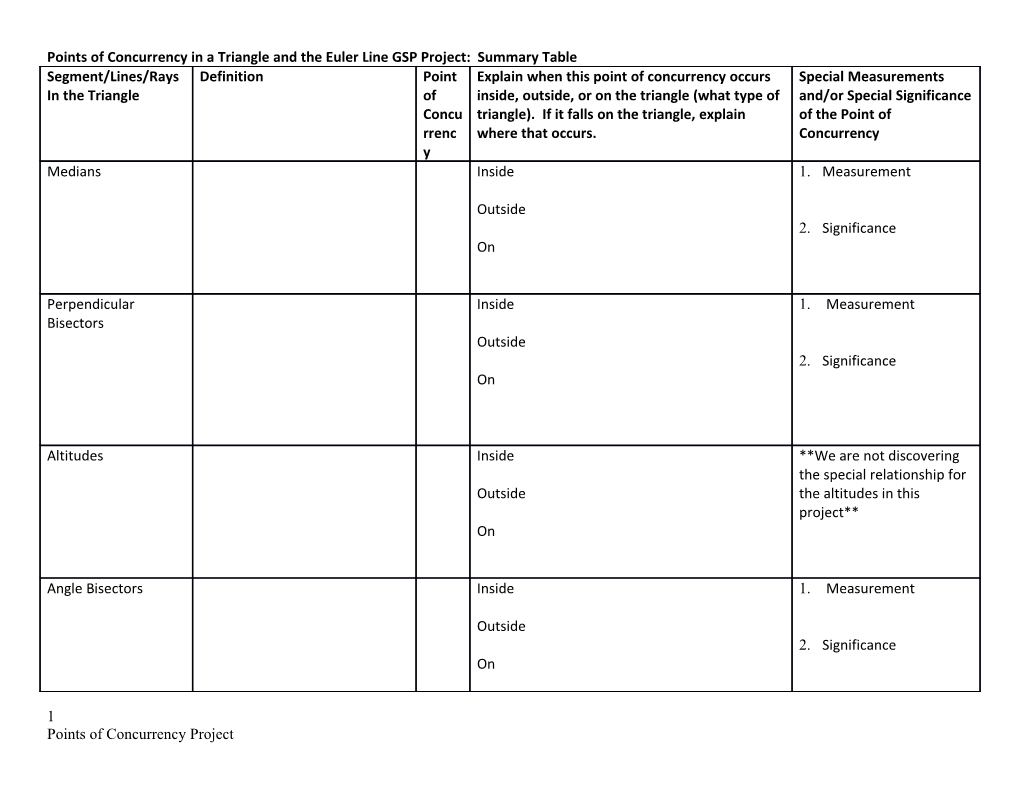
Points of Concurrency in a Triangle and the Euler Line GSP Project: Summary Table Segment/Lines/Rays Definition Point Explain when this point of concurrency occurs Special Measurements In the Triangle of inside, outside, or on the triangle (what type of and/or Special Significance Concu triangle). If it falls on the triangle, explain of the Point of rrenc where that occurs. Concurrency y Medians Inside 1. Measurement

Outside 2. Significance On

Perpendicular Inside 1. Measurement Bisectors Outside 2. Significance On

Altitudes Inside **We are not discovering the special relationship for Outside the altitudes in this project** On

Angle Bisectors Inside 1. Measurement

Outside 2. Significance On

1 Points of Concurrency Project 2 Points of Concurrency in Triangles

Essential Questions:

What are the centroid, the incenter, the circumcenter, and the orthocenter of a triangle?

How do these points of concurrency in triangles help to solve problems?

Launch:

1. Complete the Definitions Column of the Summary Table for each of the four terms (medians, perpendicular bisectors, altitudes, and angle bisectors).

2. Open the GSP file Points of Concurrency.gsp. You will notice that there are 6 pages (noted by the tabs at the bottom) to this document.

3. Construction Tab. Follow the directions given in this tab to create ONE example of each type of line/segment/ray that you just defined. Remember that GSP constructions are done by DEFINITION. For help consult the GSP HELP NOTES below (you can also consult the Help menu).

a. In triangle ABC, construct one median from any vertext to the opposite side. b. In triangle DEF, construct one altitude from any vertex to the opposite side. c. In triangle JKL, construct one perpendicular bisector of any side. d. In triangle GHI, construct one angle bisector of any angle. e. When finished, Save this file to your H: drive. Name it LastNamePC

GSP HELP NOTES:

Midpoint Selection prerequisites: One or more segments. Constructs a point at the midpoint of each selected segment. As a segment gets longer or shorter (through dragging an endpoint, for example), the midpoint moves accordingly.

Perpendicular Line Selection prerequisites: A straight object and one or more points; or a point and one or more straight objects. Constructs a line through each selected point perpendicular to each selected straight object.

Angle Bisector Selection prerequisites: Three points, with the vertex point selected second. Constructs a ray that bisects the minor angle formed by the three selected points. The second selected point designates the vertex of the angle. For instance, to bisect angle ABC, select points in the order A, then B, and finally C.

3 Points of Concurrency Project Investigation:

In this project you will investigate four different points of concurrency in a triangle.

1. Medians

a. Click on the Medians tab at the bottom of the page to study the three medians of a triangle. b. Click on Show Midpoints to see the three midpoints of the three sides. c. Click on Show Medians to view the three medians. 1-a. What do you notice about the three medians?

1-b. If you make different shaped triangles do the medians still intersect?

1-c. Does the intersection ever move out of the interior of the triangle?

d. Click on Show Centroid. This is the point of concurrency of the medians of a triangle. The centroid is sometimes referred to as the “weighted center” or balancing point of a triangle. e. Click on Show Segments to see the three medians divided into two parts each. Each median is made up of a green and red part. 1-d. What do you notice about the relationship of their lengths as you change the triangle by moving the vertices of the triangle? Which segments appear to be longer? Which segments appear to be shorter?

f. Click on Show Measure of Segments to view their length. Again move the vertices of the triangle to see how the lengths compare. g. Click on Show Ratio to see the ratio of the red segment to the green segment. Again move the vertices to change the triangle. 1-e. What do you notice about the ratio of the two parts of the median?

h. RECORD your findings in the Summary Table for medians.

4 Points of Concurrency Project 2. Perpendicular Bisectors

a. Click on the Perpendicular Bisectors tab at the bottom of the page to study the three perpendicular bisectors of a triangle. b. Click on Show Midpoints to see the three midpoints of the three sides. c. Click on Show Perpendicular Bisectors to see the three perpendicular bisectors. Move the vertices of the triangle around to change the shape of the triangle. 2-a. What do you notice about the three perpendicular bisectors? Are they always concurrent?

d. Click on the Show Intersection Circumcenter to reveal the point where the three perpendicular bisectors intersect. This is the point of concurrency of the perpendicular bisectors of a triangle. The circumcenter is the center of a special circle in relationship to the triangle. e. Click on Show Circumscribed Circle to see what circle can be constructed with the circumcenter. Move the vertices of the triangle around. 2-b. What is special about this circle?

2-c. What type of triangle can you make where the circumcenter is inside the triangle? What type of triangle can you make where the circumcenter is outside the triangle? What type of triangle can you make where the circumcenter is on the triangle? Where does it appear on the triangle?

f. Click Show Distance Measurements to show the distance from the circumcenter to each vertex. 2-d. What is always true about the distance from the cirumcenter to each of the three vertices of the triangle? Why is this true?

g. RECORD your findings in the Summary Table for perpendicular bisectors.

5 Points of Concurrency Project 3. Altitudes

a. Click on the Altitudes tab at the bottom. b. Click on Show Altitudes. Move the triangle around to confirm that these altitudes will always be concurrent. c. Click on Show Orthocenter to see the point of intersection for the three altitudes. 3-a. What type of triangle can you make where the orthocenter is inside the triangle? What type of triangle can you make where the orthocenter is outside the triangle? What type of triangle can you make where the orthocenter is on the triangle? Where does it appear on the triangle?

d. RECORD your findings in the Summary Table. We will not be discovering special properties of the orthocenter in a triangle.

4. Angle Bisectors

a. Click on the Angle Bisectors tab at the bottom. b. Click on Show Angle Bisectors. Move the triangle around to confirm that these altitudes will always be concurrent. c. Click on Show Incenter to see the point of intersection for the three angle bisectors. The incenter is the center of a special circle in relationship to the triangle. d. Click on Show Inscribed Circle to see what circle can be constructed with the incenter. Move the vertices of the triangle around. 4-a. What is special about this circle?

4-b. What type of triangle can you make where the incenter is inside the triangle? What type of triangle can you make where the incenter is outside the triangle? What type of triangle can you make where the incenter is on the triangle? Where does it appear on the triangle?

e. Click on Show Distances to Sides to show red segments indicating the distance from the incenter to each side (remember that distance is always measured at a right angle). f. Click on Show Distance Measurements. Move the triangle around. 2-d. What is always true about the distance from the incenter to each of the three vertices of the triangle? Why is this true?

g. RECORD your findings in the Summary Table for Angle Bisectors.

6 Points of Concurrency Project 5. Euler Segment

a. Click on the Euler Segment tab at the bottom. b. You see triangle ABC along with four buttons. Click on the four buttons to reveal the four points of concurrency (Centroid, circumcenter, incenter, and orthocenter). c. Move the vertices around. 5-a. Does it appear that three of the points are always collinear? Which ones? Which point is sometimes collinear with the other three?

d. Click on Show Angle Measurement and Show Lengths of Sides. Move the vertices around and watch the measurements. 4-a. What kind of triangle is created when all four points are collinear?

4-b. What kind of triangle is created when all four of the points are the same point?

e. Visit the website http://gogeometry.com/center/nine_point_center_euler.html to watch a JAVA demonstration of the Nine-Point Circle: 4-c. List the Nine Points that make up the Nine-Point Circle.

4-d. What is the significance of the Center of the Nine-Point Circle in reference to the Euler Segment?

Just for Fun: Check out the Nine-Point Circle Jigsaw Puzzle http://gogeometry.com/puzzle/euler_line_nine_point_center.htm

7 Points of Concurrency Project The Airport Problem

A county plans to build a regional airport to serve its citizens and wants to locate it within easy access of its three largest towns as shown on the map below. The county has two options for location of the new airport and is working with the airport construction company to minimize costs wherever possible. No matter where the airport is located, roads will have to be built for access directly to the towns or to the existing highways.

Option A: Build the airport at a location that is equidistant from each of the three towns. If this option is selected the county will have to pay for building new roads connecting the airport to the three towns.

Option B: Build the airport at a location that is the shortest distance from each existing highway. If this option is selected the county will have to pay for building new roads to each existing highway and pay for resurfacing each existing highway from the point of intersection leading into each town.

Cost for building new roads is $125,000 per mile. Cost for resurfacing existing highways is $50,000 per mile.

Use Geometer’s Sketchpad to determine the most cost efficient location for the new airport.

Option A: Click the Airport Problem OPTION A Tab at the bottom. Answer all the following questions.

1. If Option A is selected, which point of concurrency would be the point that is equidistant from the three towns?

2. Construct the point (Show it on your Sketch) and determine (estimate) the coordinates of the airport location.

8 Points of Concurrency Project 3. New roads will need to be constructed from this location directly to each of the three towns. Use Sketchpad to Calculate the distance from the airport location to each town.

4. Determine the cost for building the new roads (You can use the calculator in sketchpad if you want).

Option B: Click the Airport Problem OPTION B Tab at the bottom. Answer all the following questions.

1. If Option B is selected, which point of concurrency would be the point that is the shortest distance to each of the three existing highways? Hint: The shortest distance from a point to a line is the perpendicular distance.

2. Construct the point (Show it in your sketch) and determine (estimate) the coordinates of the airport location.

3. New roads will need to be constructed from this location directly to each existing highway. Use Sketchpad to find the length of each new road (distance from the point to each highway).

4. Determine the cost for building the new roads (You can use the calculator in sketchpad if you want).

5. If Option B is selected the county has also agreed to resurface the existing highways leading from the airport roads to each town. Find the cost of resurfacing the existing highways.

5. What is the cost of Option B?

6. Which option is the most cost efficient for the airport location?

7. Based on your investigation can you suggest a better solution for the county in terms of saving money on road construction? If so, how could you prove this to the county as a money saving option?

9 Points of Concurrency Project EXTRA CREDIT: Target Practice

Michael is in charge of this year’s dart tournament at the local recreation center. Instead of using a circular dartboard he decided that it would be interesting to use a square dartboard with a triangle shaped center as shown below. Points are awarded based upon how close the dart is to the centroid of the triangle. The centroid is the point of concurrency of the medians of a triangle.

1. What coordinate point represents the centroid of the triangle? Explain how you determined this.

2. The following table shows how points are awarded in this game:

Position of dart Points Inside square 5 Inside triangle 10 Within a 5 unit radius from the centroid 25 of the triangle

What is the probability of hitting: (Hint: use AREAS to determine probability) a. inside the triangle? b. within a 5 unit radius from the centroid of the triangle?

3. Michael scored 70 points during his first time up. Assuming he hit the dart board each time, what possible hits could he have made?

10 Points of Concurrency Project 11 Points of Concurrency Project