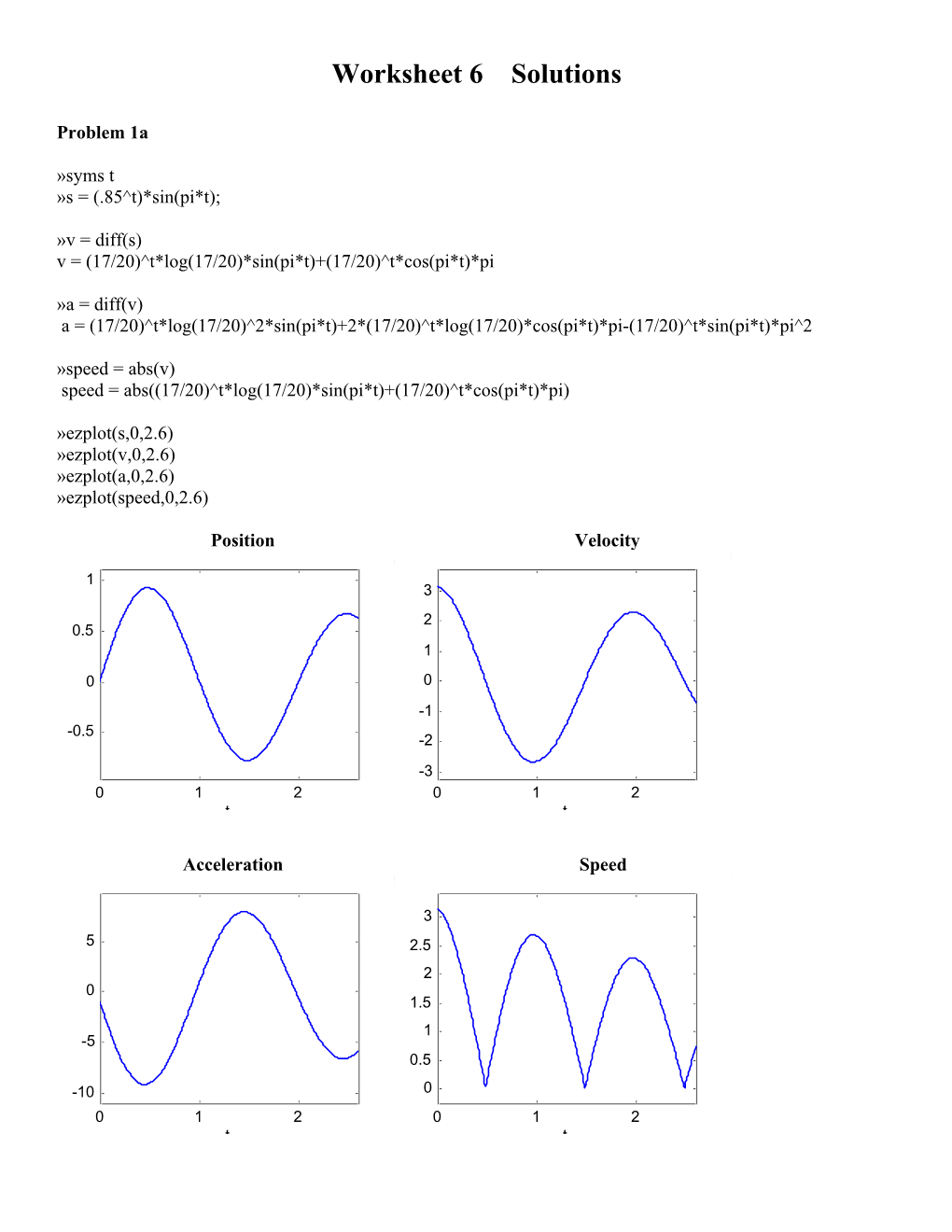
Worksheet 6 Solutions

Problem 1a

»syms t »s = (.85^t)*sin(pi*t);

»v = diff(s) v = (17/20)^t*log(17/20)*sin(pi*t)+(17/20)^t*cos(pi*t)*pi

»a = diff(v) a = (17/20)^t*log(17/20)^2*sin(pi*t)+2*(17/20)^t*log(17/20)*cos(pi*t)*pi-(17/20)^t*sin(pi*t)*pi^2

»speed = abs(v) speed = abs((17/20)^t*log(17/20)*sin(pi*t)+(17/20)^t*cos(pi*t)*pi)

»ezplot(s,0,2.6) »ezplot(v,0,2.6) »ezplot(a,0,2.6) »ezplot(speed,0,2.6)

Position Velocity (17/20)^t*sin(pi*t) (17/20)^t*log(17/20)*sin(pi*t)+(17/20)^t*cos(pi*t)*pi 1 3 2 0.5 1 0 0 -1 -0.5 -2 -3 0 1 2 0 1 2 t t

Acceleration Speed (17/20)^t*log(17/20)^2*sin(pi*t)+ ~~~ pi*t)*pi-(17/20)^t*sin(pi*t)*pi^2abs((17/20)^t*log(17/20)*sin(pi*t)+(17/20)^t*cos(pi*t)*pi)

3 5 2.5 2 0 1.5 1 -5 0.5

-10 0 0 1 2 0 1 2 t t Problem 1(b)

The particle is at rest when v(t) = 0.

»fzero('(17/20)^x*log(17/20)*sin(pi*x)+(17/20)^x*cos(pi*x)*pi',.5) ans = 0.4835

»fzero('(17/20)^x*log(17/20)*sin(pi*x)+(17/20)^x*cos(pi*x)*pi',1.5) ans = 1.4835

»fzero('(17/20)^x*log(17/20)*sin(pi*x)+(17/20)^x*cos(pi*x)*pi',2.5) ans = 2.4835

Problem 1(c)

The object is moving to the right when v > 0 and to the left when v < 0.

Right: 0

Problem 1(d) fzero('(17/20)^x*log(17/20)^2*sin(pi*x)+2*(17/20)^x*log(17/20)*cos(pi*x)*pi-(17/20)^x*sin(pi*x)*pi^2',1) ans = 0.9671

»fzero('(17/20)^x*log(17/20)^2*sin(pi*x)+2*(17/20)^x*log(17/20)*cos(pi*x)*pi-(17/20)^x*sin(pi*x)*pi^2',2) ans = 1.9671

Problem 1e

Working from the graph of speed, the particle is speeding up when the graph is increasing and slowing down when the graph is decreasing. Thus, the particle is speeding up, roughly, over the intervals 0.5

Problem 1f »ezplot(s,0,2.6) »hold on »ezplot(v,0,2.6) »ezplot(a,0,2.6) (17/20)^t*log(17/20)^2*sin(pi*t)+ ~~~ pi*t)*pi-(17/20)^t*sin(pi*t)*pi^2

-10 0 0.5 1 1.5 2 2.5 t

Problem 1g

When velocity and acceleration have the same sign, the object speeds up. When they have opposite signs, the object slows down.

Problem 1h »ezplot(s,0,50) (17/20)^t*sin(pi*t)

0.15 0.1 0.05 0 -0.05 -0.1 -0.15

0 10 20 30 40 50 t Note that sin(t) = 0 for all integer values of t, thus, to indicate the behavior of s(t) with a table requires some care.

»t= [.5 1 1.5 50.5 51 51.5 100.5 101 101.5 150.5 151 151.5]; »s = (.85.^t).*sin(pi*t); »format long »[t' s'] ans = 1.0e+02 *

0.00500000000000 0.00921954445729 0.01000000000000 0 0.01500000000000 -0.00783661278870 0.50500000000000 0.00000272681547 0.51000000000000 0.00000000000000 0.51500000000000 -0.00000231779315 1.00500000000000 0.00000000080650 1.01000000000000 -0.00000000000000 1.01500000000000 -0.00000000068552 1.50500000000000 0.00000000000024 1.51000000000000 0.00000000000000 1.51500000000000 -0.00000000000020 It appears that s(t)->0 as t->Infinity. The particle oscillates around the origin on the coordinate line with the length of the interval of oscillation approaching zero.

Problem 2(a):

(i) [F(30) - F(20)]/(30 - 20) = (20.5 - 26)/10 = -.55 dollars/passenger

(ii) [F(30) - F(25)]/(30 - 25) = (20.5 - 23)/5 = -.5 dollars/passenger

(iii) [F(40) - F(30)]/(40 - 30) = (17 - 20.5)/10 = -.35 dollars/passenger

(iv) [F(35) - F(30)]/(35 - 30) = (18.5 - 20.5)/5 = -.4 dollars/passenger

Problem 2b

Averaging the answers from (ii) and (iv) above gives an approximation of F'(30) = -.45 dollars/passenger. This means that, at 30 passengers, the fare goes down 45 cents for each additional passenger.

Problem 2c

R'(p) = [pF(p)]' = F(p) + pF'(p), so R'(30) = F(30) + 30F'(30) = 20.5 + 30(-.45) = 7.00 dollars/passenger. This means that at 30 passengers, the total revenue collected increases at the rate of $7.00 per additional passenger.