Characterizing Intermodulation Distortion of High-Power Devices
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Performance Improvement of Papr Reduction for Ofdm Signal in Lte System
International Journal of Wireless & Mobile Networks (IJWMN) Vol. 5, No. 4, August 2013 PERFORMANCE IMPROVEMENT OF PAPR REDUCTION FOR OFDM SIGNAL IN LTE SYSTEM Md. Munjure Mowla1 and S.M. Mahmud Hasan2 1Department of Electrical & Electronic Engineering, Rajshahi University of Engineering & Technology, Rajshahi, Bangladesh [email protected] 2 Department of Electronics & Telecommunication Engineering, Rajshahi University of Engineering & Technology, Rajshahi, Bangladesh [email protected] ABSTRACT Orthogonal frequency division multiplexing (OFDM) is an emerging research field of wireless communication. It is one of the most proficient multi-carrier transmission techniques widely used today as broadband wired & wireless applications having several attributes such as provides greater immunity to multipath fading & impulse noise, eliminating inter symbol interference (ISI), inter carrier interference (ICI) & the need for equalizers. OFDM signals have a general problem of high peak to average power ratio (PAPR) which is defined as the ratio of the peak power to the average power of the OFDM signal. The drawback of high PAPR is that the dynamic range of the power amplifier (PA) and digital-to-analog converter (DAC). In this paper, an improved scheme of amplitude clipping & filtering method is proposed and implemented which shows the significant improvement in case of PAPR reduction while increasing slight BER compare to an existing method. Also, the comparative studies of different parameters will be covered. KEYWORDS Bit Error rate (BER), Complementary Cumulative Distribution Function (CCDF), Long Term Evolution (LTE), Orthogonal Frequency Division Multiplexing (OFDM) and Peak to Average Power Ratio (PAPR). 1. INTRODUCTION Long term evolution (LTE) is the one of the latest steps toward the 4th generation (4G) of radio technologies designed to increase the capacity and speed of mobile telephone networks. -

Sm.1446-0 (04/2000)
Recommendation ITU-R SM.1446-0 (04/2000) Definition and measurement of intermodulation products in transmitter using frequency, phase, or complex modulation techniques SM Series Spectrum management ii Rec. ITU-R SM.1446-0 Foreword The role of the Radiocommunication Sector is to ensure the rational, equitable, efficient and economical use of the radio-frequency spectrum by all radiocommunication services, including satellite services, and carry out studies without limit of frequency range on the basis of which Recommendations are adopted. The regulatory and policy functions of the Radiocommunication Sector are performed by World and Regional Radiocommunication Conferences and Radiocommunication Assemblies supported by Study Groups. Policy on Intellectual Property Right (IPR) ITU-R policy on IPR is described in the Common Patent Policy for ITU-T/ITU-R/ISO/IEC referenced in Resolution ITU-R 1. Forms to be used for the submission of patent statements and licensing declarations by patent holders are available from http://www.itu.int/ITU-R/go/patents/en where the Guidelines for Implementation of the Common Patent Policy for ITU-T/ITU-R/ISO/IEC and the ITU-R patent information database can also be found. Series of ITU-R Recommendations (Also available online at http://www.itu.int/publ/R-REC/en) Series Title BO Satellite delivery BR Recording for production, archival and play-out; film for television BS Broadcasting service (sound) BT Broadcasting service (television) F Fixed service M Mobile, radiodetermination, amateur and related satellite services P Radiowave propagation RA Radio astronomy RS Remote sensing systems S Fixed-satellite service SA Space applications and meteorology SF Frequency sharing and coordination between fixed-satellite and fixed service systems SM Spectrum management SNG Satellite news gathering TF Time signals and frequency standards emissions V Vocabulary and related subjects Note: This ITU-R Recommendation was approved in English under the procedure detailed in Resolution ITU-R 1. -

Third Order Intercept Point
Third Order Intercept Point Third order intercept point (IP3) is a term sometimes heard when amateur radio operators are discussing the qualities, or lack thereof, of a receiver. Third order intercept point is just one of several specifications that can be used to judge the quality of a receiver. Some of the other specifications such as signal to noise ratio and selectivity are relatively easy to understand and interpret. It should be pointed out that in many instances complete specifications are not provided in manufacturing literature and must be obtained from independent testing sources or through other means. The term is somewhat involved and many people don’t actually know what it really means. Most who us it do know that the higher the number the better the receiver. Numbers may range from something like –10db to something in the range of +30 to 40 db. In very simple terms IP3 is a way of expressing how well a receiver separates two closely spaced signals. However, there is a second part that creates confusion. This second part will be the basis for our discussion. It is based one the two closely spaced signals just mentioned. Lets be clear that IP3 is a theoretical point that is calculated and is not measured as is specifications such as selectivity. All modern receivers have at least one intermediate frequency (IF) between their antenna input and their audio amplification stages which drive the speaker. Most have at least two and in some models three mixers. When a single signal is received and processed it of course can be easily heard and understood. -
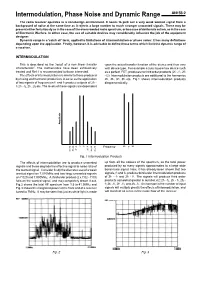
Intermodulation, Phase Noise and Dynamic Range AN156-2 the Radio Receiver Operates in a Non-Benign Environment
Intermodulation, Phase Noise and Dynamic Range AN156-2 The radio receiver operates in a non-benign environment. It needs to pick out a very weak wanted signal from a background of noise at the same time as it rejects a large number to much stronger unwanted signals. These may be present either fortuitously as in the case of the overcrowded radio spectrum, or because of deliberate action, as in the case of Electronic Warfare. In either case, the use of suitable devices may considerably influence the job of the equipment designer. Dynamic range is a 'catch all' term, applied to limitations of intermodulation or phase noise: it has many definitions depending upon the application. Firstly, however, it is advisable to define those terms which limit the dynamic range of a receiver. INTERMODULATION This is described as the 'result of a non linear transfer upon the actual transfer function of the device and thus vary characteristic’. The mathematics have been exhaustively with device type. For example a truly square law device such treated and Ref.1 is recommended to those interested. as a perfect FET, produces no third order products (2f2 - f1, 2f1 The effects of intermodulation are similar to those produced - f2). Intermodulation products are additional to the harmonics by mixing and harmonic production, in so far as the application 2f1, 2f2, 3f1, 3f2 etc. Fig.1 shows intermodulation products of two signals of frequencies f1 and f2 produce outputs of 2f2 - diagrammatically. f1 2f1 - f2, 2f1, 2f2 etc. The levels of these signals are dependent Amplitude 2 2 2 1 1 1 f1 f2 2f1 2 2f2 -f -f Frequency +f 1 2 -3f -2f -2f -3f 1 f 1 1 2 2 2f 2f 4f 3f 3f 4f Fig. -

IQ, Image Reject, & Single Sideband Mixer Primer
ICROWA M VE KI , R IN A C . M . S 1 H IQ, IMAGE REJECT 9 A 9 T T 1 E E R C I N N I G & single sideband S P S E R R E F I O R R R M A A B N E C Mixer Primer Input Isolated By: Doug Jorgesen introduction Double Sideband Available P Bandwidth Wireless communication and radar systems are under continuous pressure to reduce size, weight, and power while increasing dynamic range and bandwidth. The quest for higher performance in a smaller 1A) Double IF I R package motivates the use of IQ mixers: mixers that can simultaneously mix ‘in-phase’ and ‘quadrature’ Sided L P components (sometimes called complex mixers). System designers use IQ mixers to eliminate or relax the Upconversion ( ) ( ) f Filter Filtered requirements for filters, which are typically the largest and most expensive components in RF & microwave Sideband system designs. IQ mixers use phase manipulation to suppress signals instead of bulky, expensive filters. LO푎 푡@F푏LO1푡 FLO1 The goal of this application note is to introduce IQ, single sideband (SSB), and image reject (IR) mixers in both theory and practice. We will discuss basic applications, the concepts behind them, and practical Single Sideband considerations in their selection and use. While we will focus on passive diode mixers (of the type Marki Mixer I R sells), the concepts are generally applicable to all types of IQ mixers and modulators. P 0˚ L 1B) Single IF 0˚ P Sided Suppressed Upconversion I. What can an IQ mixer do for you? 90˚ Sideband ( ) ( ) f 90˚ We’ll start with a quick example of what a communication system looks like using a traditional mixer, a L I R F single sideband mixer (SSB), and an IQ mixer. -

TSEK38: Radio Frequency Transceiver Design Lecture 2
"2 Repetion of Lecture 1 TSEK38: Radio Frequency • Wireless communication systems today Transceiver Design • Some wireless standards Lecture 2: Fundamentals of • Communication radio examples System Design • Architectures: the big picture Ted Johansson, ISY [email protected] TSEK38 Radio Frequency Transceiver Design 2019/Ted Johansson "3 "4 Lisam Course Room There is a standard for almost any need! • https://liuonline.sharepoint.com/sites/TSEK38/TSEK38_2019VT_FU Mobility Data rate Mb/s TSEK38 Radio Frequency Transceiver Design 2019/Ted Johansson TSEK38 Radio Frequency Transceiver Design 2019/Ted Johansson "5 "6 Examples of Standards 5G Standard Access Frequency Channel Frequency Modulation Rate Peak Power Scheme/Dupl band (MHz) Spacing Accuracy Technique (kb/s) (uplink) GSM TDMA/FDMA/ 890-915 (UL) 200 kHz 90 Hz GMSK 270.8 0.8, 2, TDD 935-960 (DL) 5, 8 W DCS-1800 TDMA/FDMA/ 1710-1785 (UL) 200 kHz 90 Hz GMSK 270.8 0.8, 2, TDD 1805-1850 (DL) 5, 8 W DECT TDMA/FDMA/ 1880-1900 1728 kHz 50 Hz GMSK 1152 250 mW TDD IS-95 CDMA/ FDMA/ 824-849 (RL) 1250 N/A OQPSK 1228 N/A cdmaOne FDD 869-894 (FL) kHz Bluetooth FHSS/TDD 2400-2483 1 MHz 20 ppm GFSK 1000 1,4,100 mW 802.11b CDMA/TDD 2400-2483 20 MHz 25 ppm QPSK/CCK 1, 2, 11 1 W (DSSS) Mb/s WCDMA W-CDMA/TD- 1920-1980 (UL) 5 MHz 0.1 ppm QPSK, 3840 0.125, 0.25, (UMTS) CDMA/F/TDD 2110-2170 (DL) 16/64QAM (max) 0.5, 2W LTE OFDMA (DL) 700-2700 scalable 4.6 ppm QPSK, DL/UL Scalable SC-FDMA (UL) to 20MHz /32 ppm 16/64QAM 300/75 with BW to FDD/TDD 0.1 ppm (BS) Mb/s 250 mW Source: 5G RF for dummies (Corvo) TSEK38 -

Lecture 9: Intercept Point, Gain Compression and Blocking
EECS 142 Lecture 9: Intercept Point, Gain Compression and Blocking Prof. Ali M. Niknejad University of California, Berkeley Copyright c 2005 by Ali M. Niknejad A. M. Niknejad University of California, Berkeley EECS 142 Lecture 9 p. 1/29 – p. 1/29 Gain Compression dVo dVo dVi dVi V o Vo V i Vi The large signal input/output relation can display gain compression or expansion. Physically, most amplifier experience gain compression for large signals. The small-signal gain is related to the slope at a given point. For the graph on the left, the gain decreases for increasing amplitude. A. M. Niknejad University of California, Berkeley EECS 142 Lecture 9 p. 2/29 – p. 2/29 1dB Compression Point P o,−1 dB ¯ ¯ ¯Vo ¯ ¯ ¯ ¯ Vi ¯ V P i i,−1 dB Gain compression occurs because eventually the output signal (voltage, current, power) limits, due to the supply voltage or bias current. If we plot the gain (log scale) as a function of the input power, we identify the point where the gain has dropped by 1 dB. This is the 1 dB compression point. It’s a very important number to keep in mind. A. M. Niknejad University of California, Berkeley EECS 142 Lecture 9 p. 3/29 – p. 3/29 Apparent Gain Recall that around a small deviation, the large signal curve is described by a polynomial 2 3 so = a1si + a2s + a3s + i i · · · For an input si = S1 cos(ω1t), the cubic term generates 3 3 3 1 S1 cos (ω1t) = S1 cos(ω1t) (1 + cos(2ω1t)) 2 3 1 2 = S1 cos(ω1t) + cos(ω1t) cos(2ω1t) 2 4 Recall that 2 cos a cos b = cos(a + b) + cos(a b) − 3 1 1 = S1 cos(ω1t) + (cos(ω1t) + cos(3ω1t)) 2 4 A. -

Input Third Order Intercept Point for Crystal Filters
High Frequency Design Crystal Filters Input Third Order Intercept Point for Crystal Filters By Dennis Layne Introduction Δ = difference between desired signal and A key performance The heart of a dual unwanted distortion (dB) requirement for crystal IF conversion super hetero- n = order of distortion filters is the linearity of dyne receiver is the the filter. Intermediate frequency Two Tone Test (IF) filter or filters. This The Two-Tone test measures the third- filter has to be approximately one channel order distortion products produced by a non- wide. Crystal IF filters are typically used in linear device when two tones closely spaced in order to achieve this bandwidth. A key perfor- frequency are fed into its input. In the case of mance requirement for crystal IF filters is the an IF crystal filter, the two tones may be linearity of the filter. The IF filter is often sub- spaced the same as the industry standard jected to multiple strong signals that are not in intermodulation rejection test. These tones the pass band of the filter. In order to predict are outside of the filter passband. As a result the receiver’s linear dynamic range it is com- of frequency spacing, the difference between mon to calculate the overall cascaded input the “test signal” and the “unwanted distortion” third order intercept point (IIP3). From this cannot be measured directly in one step. value an estimate of the receiver intermodula- The power of the distortion product is only tion rejection can be calculated. Since crystal meaningful at the output of the device under filters are passive components and by design, test and the gain of the device is defined as the the interfering signals are not in the pass band loss in the passband of the filter. -

Noise Power Ratio Testing of Multichannel Single Sideband Communication Equipment Per Vinther
Rochester Institute of Technology RIT Scholar Works Theses Thesis/Dissertation Collections 1969 Noise Power Ratio testing of multichannel single sideband communication equipment Per Vinther Follow this and additional works at: http://scholarworks.rit.edu/theses Recommended Citation Vinther, Per, "Noise Power Ratio testing of multichannel single sideband communication equipment" (1969). Thesis. Rochester Institute of Technology. Accessed from This Thesis is brought to you for free and open access by the Thesis/Dissertation Collections at RIT Scholar Works. It has been accepted for inclusion in Theses by an authorized administrator of RIT Scholar Works. For more information, please contact [email protected]. NOISE POWER RATIO TESTING OF MULTICHANNEL SINGLE SIDEBAND COMMUNICATION EOUIPMENT prepared by PER VINTHER A Thesis Submitted in Partial Fulfillment of the Requirements for the Degree of MASTER OF SCIENCE in ELECTRICAL ENGINEERING Approved by. Prof. Name Illegible (Theais Advisor) Prof. Name Illegible Prof. _________- __________ Prof. W. F. Walker (Department Head) DEPARTMENT OF ELECTRICAL ENGINEERING COLLEGE OF APPLIED SCIENCE ROCHESTER INSTITUTE OF TECHNOLOGY ROCHeSTER NEW YORK June 1969 ABSTRACT It is shown, that Noise Power Ratio (NPR) testing of mul tichannel Single Sideband (SSB) transmitters should be perform ed loading all channels with identical white, gaussian, zero- mean noise signals in order to obtain the worst case result. A theoretical analysis of bichannel equipment under the two different input conditions* (a) statistically independent noise signals, and (b) statistically dependent noise signals? shows that the intermodulation distortion on the output of the transmitter is the same for either case. This result is extended for an arbitrary number of chan nels to the point of showing that the test results obtained for statistically dependent noise inputs will be either equal to or worse than those obtained for statistically independent noise inputs. -

Solving Your Radio Frequency Interference Problems Spectrum
Application Note Solving Your Radio Frequency Interference Problems MS2721B, MS2723B, MS2724B Spectrum Master™ RF interference takes many forms. In this application note we discuss how to detect and eliminate, or at least reduce, interference caused by discrete emitters. These emitters may be devices intended to be transmitters or they may be devices that due to design flaws or malfunctions are radiating signals where they shouldn’t be. We will also discuss interference caused by intermodulation. We specifically do not discuss power line interference, which is too broad a topic to be given proper treatment here. Interference can occur at any frequency from below the AM broadcast band to microwave link frequencies and beyond. The Problem As more and more diverse uses for the radio spectrum emerge, the number of signals that may potentially cause interference inexorably increases. There are literally millions of radiators in operation at any one time in relatively small geographic areas. For example, in California there are more than 700 pages of commercial and government licensed emitters covering the state and the radio spectrum. In some cases a single license may covers dozens or hundreds of mobile users who could show up next to your site and unintentionally cause problems. That list doesn’t include licensed private radio systems such as Amateur Radio, and GMRS. Of which there are over 100,000 in the state. As big as those numbers seem, they are tiny compared to the numbers of unlicensed emitters such as Bluetooth, Wi-Fi, wireless microphones, remote control cars, etc. And those numbers are small compared to the numbers of unintentional emitters such as TV and radio receivers, microwave ovens – basically any device that contains an oscillator or that, due to failure or poor design, oscillates and radiates signals. -

Lecture 8: Distortion Metrics
EECS 142 Lecture 8: Distortion Metrics Prof. Ali M. Niknejad University of California, Berkeley Copyright c 2005 by Ali M. Niknejad A. M. Niknejad University of California, Berkeley EECS 142 Lecture 8 p. 1/26 – p. 1/26 Output Waveform In general, then, the output waveform is a Fourier series vo = Vˆo1 cos ω1t + Vˆo2 cos2ω1t + Vˆo3 cos3ω1t + . Vˆo 100mV 10mV 1mV Gain Compression Higher Order 100µV Distortion Products Vˆo2 10µV Vˆo3 1µV Vˆi 1µV 10µV 100µV 1mV 10mV A. M. Niknejad University of California, Berkeley EECS 142 Lecture 8 p. 2/26 – p. 2/26 Fractional Harmonic Distortion The fractional second-harmonic distortion is a commonly cited metric ampl of second harmonic HD2 = ampl of fund If we assume that the square power dominates the second-harmonic 2 S1 a2 2 HD2 = a1S1 or 1 a2 HD2 = 2 S1 a1 A. M. Niknejad University of California, Berkeley EECS 142 Lecture 8 p. 3/26 – p. 3/26 Third Harmonic Distortion The fractional third harmonic distortion is given by ampl of third harmonic HD3 = ampl of fund If we assume that the cubic power dominates the third harmonic 2 S1 a3 4 HD3 = a1S1 or 1 a3 2 HD3 = S1 4 a1 A. M. Niknejad University of California, Berkeley EECS 142 Lecture 8 p. 4/26 – p. 4/26 Output Referred Harmonic Distortion In terms of the output signal Som, if we again neglect gain expansion/compression, we have Som = a1S1 1 a2 HD2 = 2 Som 2 a1 1 a3 2 HD3 = 3 Som 4 a1 On a dB scale, the second harmonic increases linearly with a slope of one in terms of the output power whereas the thrid harmonic increases with a slope of 2. -

Application Note Intermodulation Distortion
Intermodulation Distortion Measurements on Modern Spectrum Analyzers Application Note Products: | R&SFSV | R&SFSW This Application Note describes the differences in intermodulation distortion measurements between traditional spectrum analyzers with analog narrow- band IF signal path and modern spectrum analyzers using a wide-band IF signal path and digital RBW filters. _2E 79 1EF – Application Application Note Dr. Florian Ramian June 2012 Table of Contents Table of Contents 1 Introduction ............................................................................ 3 2 Intermodulation Distortion .................................................... 3 2.1 Harmonic signals ......................................................................................... 3 2.2 Intermodulation as a result of harmonic signals ...................................... 4 2.3 Characterizing IMD ....................................................................................... 4 3 Comparison of Architectures ................................................ 7 3.1 Traditional swept spectrum analyzers ....................................................... 7 3.2 Modern wide-band (signal- and) spectrum analyzers .............................. 8 3.3 Comparison .................................................................................................10 3.4 Impact of electronic attenuators and RF preamplifiers ..........................12 4 Measurement of Intermodulation Distortion ...................... 14 4.1 Measurement setup ....................................................................................14