DOCSLIB.ORG

Bi Electrodeposition on Pt in Acidic Medium 2. Hydrodynamic Voltammetry

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Bi Electrodeposition on Pt in Acidic Medium 2. Hydrodynamic Voltammetry CHEMIJA. 2006. Vol. 17. No. 2–3. P. 11–15 © Lietuvos mokslų akademija,Bi electrodeposition 2006 on Pt in acidic medium. 2. Hydrodynamic voltammetry 11 © Lietuvos mokslų akademijos leidykla, 2006 Bi electrodeposition on Pt in acidic medium 2. Hydrodynamic voltammetry Ignas Valsiūnas*, A Pt rotating disc was used to provide some kinetic information concerning the electrodeposition of bismuth from Bi3+ acidic perchlorate solution 1 M Laima Gudavičiūtė, HClO4 + 0.05 M Bi(ClO4)3 at 20 °C. The electrodeposition of Bi from this solution may be interpreted in terms of an irreversible stepwise discharge of Vidmantas Kapočius and Bi3+ ions proceeding either through three successive one-electron steps with the transfer of the first electron as the rate-limiting step or via two successive Antanas Steponavičius steps with the transfer of two electrons in the first stage as the rate-limiting step. From the experimental data the diffusion coefficient D for Bi3+ ion was Institute of Chemistry, calculated and was found to be 4.9 · 10-6 cm2 s-1. A. Goštauto 9, LT-01108 Vilnius, Lithuania Key words: bismuth, electrodeposition, perchlorate solutions, Pt rotating disc electrode, rate-determining steps INTRODUCTION technique was therefore employed in order to elucidate the further information on the mechanism of Bi Although bismuth, as a semimetal, exhibits some unusual electrochemical deposition on a polycrystalline Pt thermal, electrical and magnetic properties that make its (Pt(poly)) electrode. actual and potential applications [1, 2] to be rather wide, its electrochemical reduction from Bi3+ solutions has not EXPERIMENTAL been studied very extensively. Several electrochemical studies have been devoted to the investigation of current- Details on the preparation of perchlorate Bi3+ solution, potential (i/E) characteristics [3–7]. In most investigations on the electrochemical cell, instrumentation and the pre- of Bi deposition only electrolysis in an unstirred Bi3+ paration of a Pt RDE (1 cm2 in area) have been repor- solution under a potential control has been employed, ted previously [7]. The working solution containing 0.05 and these cannot give sufficient information on the M Bi(ClO4)3 + 1 M HClO4 was used for electrochemi- kinetics and mechanism of the process. Such statement cal measurements. The potential of Pt RDE (E) was can be supported by the results of our recent work [7] scanned slowly (5 mV s-1) during rotation. All poten- in which we have shown that the experimental tials in the paper are quoted versus the standard hydro- relationships between the characteristics of cyclic gen electrode (SHE). voltammograms (CVs) and the conditions of electrolysis, including the Bi3+ concentration (c), potential sweep rate THEORETICAL ANALYSIS (v) and the number of cycles (n) during a successive cycling do not completely satisfy the diagnostic criteria For a bare rotating disc electrode, the current measured for a reversible or a totally irreversible electrochemical under non-limiting conditions is related to the kinetic reaction predicted by the cyclic voltammetry (CV) theory and diffusion-controlled currents by the Levich–Kou- [8, 9]. On the basis of these results, it has been suggested tecky (K–L) equation [11]: [7] that charge transfer during the Bi deposition onto a 1/i = 1/i + 1/Bw1/2, (1) Pt electrode should be a more complex process consisting kin of several separate steps. where ikin is the kinetically controlled current in the To the best of our knowledge, there is only one absence of the mass transfer effects and B is the inver- work [10] in which the voltammetric data, under se of the K-L slope at each potential. In the diffusion- hydrodynamically-defined conditions, have been reported controlled region, the limiting current ilim is described for the electrodeposition of Bi. by the following Levich (L) equation [11] : In the present study, which is a continuation of our i = 0.62nFAD2/3cν-1/6w1/2, (2) previous work [7], a rotating disc electrode (RDE) lim where n, D, A, n, c and w are the number of the * Corresponding author. E-mail: [email protected] exchanged electrons, diffusion coefficient (cm2 s-1), 12 Ignas Valsiūnas, Laima Gudavičiūtė, Vidmantas Kapočius and Antanas Steponavičius apparent area of RDE (cm2), kinematic viscosity (cm2 (the symmetry factor) of the rds, A is the electrode s-1), bulk concentration of a reactant (mol cm-3) and surface area. RDE rotation rate (rad s-1), respectively. The kinetic The overall current is current is described by the following equation [11] : -i = n(i –i ) = i – i ,(11) fm bm f b ikin = nFAkf c, (3) where i denotes the overall reaction net current which where k is the potential-dependent forward rate constant f is negative for the reduction reaction, i is the back- and the other variables are as described above. bm ward reaction current of the rds, i and i represent the It is generally agreed [11–13] that if more than one f b forward and backward reaction current of the overall electron is transferred during an electrode reaction, the reaction, respectively. mechanism of such process is usually analyzed using Then, following the considerations in the literature, the following simplifying assumptions: (i) only one elec- e.g. [14], the overall current can be represented as fol- tron is transferred in an elementary step; (ii) one of the lows: elementary steps is much slower than the others and, therefore, is a rate-determining step (rds), the elemen- α η α η -i = i0{exp[(m + c)(F /RT)]-exp[-(n – m - a)(F / tary processes preceding the rds are at quasi-equilib- RT)]} = i [exp(α Fη/RT) – exp(-α Fη/RT)], (12) rium. Then, considering the reduction reaction invol- 0 c,app a,app ving the transfer of n electrons, where i0 is the exchange current at the equilibrium po- tential E , α and a are the cathodic and anodic trans- → eq c a O + ne R (4) α α α fer coefficients of the rds, c,app = m + c and a,app = α the sequence of steps can be described as follows n – m – a are the apparent transfer coefficients, res- α α (see, e. g. [14]): pectively. Obviously, there is c,app + a,app = n and α /α = (m + α )/(n – m – α ), while α + α =1, O + e → A (5a) c,app a,app c a c a 1 which only holds if the same step remains rate-control- A + e → A m steps are in equilibrium (5b) 1 2 ling over the wide range of the η involved [13]. The ………….. stoichiometric number ν* here is assumed to be 1. In A + e → A (5c) m-1 m α α most systems c or a turns out to lie between 0.3 and → Am + e Am+1 rds (5d) 0.7, and it can be approximated to 0.5 in the absence of actual measurements. A + e → A (5e) m+1 m+2 In the case of the overall electrode reaction studied …………… (n – m – 1) steps are in equilibrium 3+ → → Bi + 3e Bi (13) An-1 + e R (5f) α α α α The concentration of A1 at the surface of the elec- n = 3, c,app/ a,app = (m + c)/(3 – m – a). Then, if trode (c1) can be determined from the Nernst equation: the transfer of the 1st electron is the rds, m = 0, and 0 α α α α α E = E1 + (RT/F)ln(c0/c1) (6) c,app/ a,app = c/(3 – a). c is predicted to be equal to α c1 = K1c0exp(-FE/RT), (7) c,app. If the transfer of the 2nd electron is the rds, then 0 α α α α α where E1 is the formal electrode potential of the reac- m = 1, c,app = 1 + c and ac,app/ a,app = (1 + c)/(2 – a). tion of the 1st electron transfer, the constant If the transfer of the 3rd electron is the rds, then m = 0 α α α α α α K1 = exp(FE1 /RT). 2, c,app = 2 + c and c,app/ a,app = (2 + c)/(1 – a). Similarly, For multistep electrode reactions, in the absence of mass-transport limitations and at high overpotentials, η, c = K c exp(-FE/RT) = K K c exp(-2FE/RT) (8) 2 2 1 2 1 0 η particularly, at high c, the cathodic Tafel slope bc = δη δ α cm = Kmcm-1exp(-FE/RT) = Kfc0exp(-mFE/RT), (9) c/ log|i| = 2.303RT/ c,appF. Then, for the overall elec- trode reaction (13) and taking ν* = 1, T = 293K, the where the constant K = exp(FE 0/RT), i = 1, 2,…m, m i following experimental values of b can be predicted: m c m 116, ca. 39 and ca. 23 mV dec-1 for the transfer of the and the constant K = ∏ K = exp[(F/RT) 0]. f i ∑ E i 1st, 2nd and 3rd electron as the rds, respectively. i = 1 = i 1 In general (see, e.g. [13]), most electrode processes, The forward reaction current of the rds, i , can be fm especially those with more than one charge transfer expressed as follows [14]: event, may also involve adsorption and desorption of 0 primary reactants, intermediates and ultimate products. i = 0 c exp[–(α F/RT)(E- E + )] = fm FAk m+1 m c m 1 On the other hand, in general, for such complex elec- α trochemical systems, there is a certain difficulty in a = 0 (K ) c K c exp[-(m + α )(FE/RT)], (10) FAk m+1 m+1 f 0 c making distinction between the overall n value of the electrode reaction (4) and the number of electrons of 0 where k m+1 is the standard reaction rate constant at the rds, usually designed as z because the latter may 0 + α E m 1 of the rds, c is the cathodic transfer coefficient not be readily apparent.
Load more

Recommended publications
  • 07 Chapter2.Pdf
    22 METHODOLOGY 2.1 INTRODUCTION TO ELECTROCHEMICAL TECHNIQUES Electrochemical techniques of analysis involve the measurement of voltage or current. Such methods are concerned with the interplay between solution/electrode interfaces. The methods involve the changes of current, potential and charge as a function of chemical reactions. One or more of the four parameters i.e. potential, current, charge and time can be measured in these techniques and by plotting the graphs of these different parameters in various ways, one can get the desired information. Sensitivity, short analysis time, wide range of temperature, simplicity, use of many solvents are some of the advantages of these methods over the others which makes them useful in kinetic and thermodynamic studies1-3. In general, three electrodes viz., working electrode, the reference electrode, and the counter or auxiliary electrode are used for the measurement in electrochemical techniques. Depending on the combinations of parameters and types of electrodes there are various electrochemical techniques. These include potentiometry, polarography, voltammetry, cyclic voltammetry, chronopotentiometry, linear sweep techniques, amperometry, pulsed techniques etc. These techniques are mainly classified into static and dynamic methods. Static methods are those in which no current passes through the electrode-solution interface and the concentration of analyte species remains constant as in potentiometry. In dynamic methods, a current flows across the electrode-solution interface and the concentration of species changes such as in voltammetry and coulometry4. 2.2 VOLTAMMETRY The field of voltammetry was developed from polarography, which was invented by the Czechoslovakian Chemist Jaroslav Heyrovsky in the early 1920s5. Voltammetry is an electrochemical technique of analysis which includes the measurement of current as a function of applied potential under the conditions that promote polarization of working electrode6.
    [Show full text]
  • Hydrodynamic Voltammetry As a Rapid and Simple Method for Evaluating Soil Enzyme Activities
    Sensors 2015, 15, 5331-5343; doi:10.3390/s150305331 OPEN ACCESS sensors ISSN 1424-8220 www.mdpi.com/journal/sensors Article Hydrodynamic Voltammetry as a Rapid and Simple Method for Evaluating Soil Enzyme Activities Kazuto Sazawa 1,* and Hideki Kuramitz 2 1 Center for Far Eastern Studies, University of Toyama, Gofuku 3190, 930-8555 Toyama, Japan 2 Department of Environmental Biology and Chemistry, Graduate School of Science and Engineering for Research, University of Toyama, Gofuku 3190, 930-8555 Toyama, Japan; E-Mail: [email protected] * Author to whom correspondence should be addressed; E-Mail: [email protected]; Tel./Fax: +81-76-445-66-69. Academic Editor: Ki-Hyun Kim Received: 26 December 2014 / Accepted: 28 February 2015 / Published: 4 March 2015 Abstract: Soil enzymes play essential roles in catalyzing reactions necessary for nutrient cycling in the biosphere. They are also sensitive indicators of ecosystem stress, therefore their evaluation is very important in assessing soil health and quality. The standard soil enzyme assay method based on spectroscopic detection is a complicated operation that requires the removal of soil particles. The purpose of this study was to develop a new soil enzyme assay based on hydrodynamic electrochemical detection using a rotating disk electrode in a microliter droplet. The activities of enzymes were determined by measuring the electrochemical oxidation of p-aminophenol (PAP), following the enzymatic conversion of substrate-conjugated PAP. The calibration curves of β-galactosidase (β-gal), β-glucosidase (β-glu) and acid phosphatase (AcP) showed good linear correlation after being spiked in soils using chronoamperometry.
    [Show full text]
  • Effective and Novel Application of Hydrodynamic Voltammetry to the Study of Superoxide Radical Scavenging by Natural Phenolic Antioxidants
    antioxidants Article Effective and Novel Application of Hydrodynamic Voltammetry to the Study of Superoxide Radical Scavenging by Natural Phenolic Antioxidants Stuart Belli 1,*, Miriam Rossi 1,*, Nora Molasky 1, Lauren Middleton 1, Charles Caldwell 1, Casey Bartow-McKenney 1, Michelle Duong 1, Jana Chiu 1, Elizabeth Gibbs 1, Allison Caldwell 1, Christopher Gahn 2 and Francesco Caruso 1 1 Department of Chemistry, Vassar College, Poughkeepsie, NY 12604, USA; [email protected] (N.M.); [email protected] (L.M.); [email protected] (C.C.); [email protected] (C.B.-M.); [email protected] (M.D.); [email protected] (J.C.); [email protected] (E.G.); [email protected] (A.C.); [email protected] (F.C.) 2 Computing & Information Services, Vassar College, Poughkeepsie, NY 12604, USA; [email protected] * Correspondence: [email protected] (S.B.); [email protected] (M.R.) Received: 18 November 2018; Accepted: 25 December 2018; Published: 4 January 2019 Abstract: The reactions of antioxidants with superoxide radical were studied by cyclic voltammetry (CV)—and hydrodynamic voltammetry at a rotating ring-disk electrode (RRDE). In both methods, the superoxide is generated in solution from dissolved oxygen and then measured after being allowed to react with the antioxidant being studied. Both methods detected and measured the radical scavenging but the RRDE was able to give detailed insight into the antioxidant behavior. Three flavonoids, chrysin, quercetin and eriodictyol, were studied, their scavenging activity of superoxide was assessed and the molecular structure of each flavonoid was related to its scavenging capability. From our improved and novel RRDE method, we determine the ability of these 3 antioxidants to react with superoxide radical in a more quantitative manner than the classical CV.
    [Show full text]
  • Modelling of the Rotating Disk Electrode in Ionic Liquids: Difference Between Water Based and Ionic Liquids Electrolytes
    Modelling of the rotating disk electrode in Ionic liquids: difference between water based and ionic liquids electrolytes A. Giaccherini1, A. Lavacchi2 1INSTM, Firenze, Italy, 2ICCOM - CNR, Firenze, Italy *Corresponding author: via Lastruccia 3-13 50019, Sesto Fiorentino (FI), [email protected] Abstract: The last few years experienced a The former allows to validate the model by rapid growth in the application of Ionic means of comparison with the experimental Liquids (IL’s) to electrodeposition. ILs voltammograms, the last allows to offer a variety of advantages over aqueous rationalize the peculiar mass transport electrolytes. In general ILs show large properties of the Ils. In particular, thanks to chemical and thermal stability, high ionic the comparison of the concentration profiles conductivity and an electrochemical window and fluxes at the steady and quasi-steady much larger than water. These properties states of the potential scan for both systems, together with their negligible vapor pressure we clarified the nature of the unexpected enabling their use at different temperatures peaks show by the experimental without any risk of generating harmful voltammograms. vapors and joined to the absence of hydrogen discharge interfering with Keywords: Levich equation, Ionic Liquids, electrodeposition processes, as they are Transport proprieties, RDE, essentially hydrophobic, make them the best electroanalytical, CFD. candidates to be used for the obtainment of homogeneous electrodeposited thin films. 1. Introduction This study focuses on the silver electrodeposition from a silver Research on electrodeposition has recently tetrafluoroborate solution in 1-butyl-3- focused on the quest for new electrolytes methyltetrafluoroborate BMImBF4. We alternative to water. This was mainly driven notice that practical deposition rate at even by the need to develop new and green concentrations were much lower in ionic electrodeposition processes.
    [Show full text]
  • ALS Product Catalog Information
    ALS Product Catalog Instrumentation Vol. 019A Working Electrodes Working Variety of products line up for research purposes Counter Electrodes RRDE-3A Reference ElectrodesReference Cells Voltammetry Flow Cells Model2325 SEC2020 Spectroelectrochemistry Others Electrochemistry General Catalog Information Technical notes and Movie library ALS technical notes and movie https://www.als-japan.com/technical-note.html frontpage --> Technical note ALS website has a "Technical note" and "Movie library" section, where you will find useful information and introduction movie of the products. For the instrument, set up and application movies will help you in the choose of the accessories. We will be always producing and releasing new movies, attending the demands of spectators. Inspection data sheet download service https://www.als-japan.com/dl/ Inspection data sheet link frontpage --> Support --> Electrode data ALS working and reference electrodes are tested and inspected before shipment, and the check data could be confirmed through the website. In the instruction manual, for the product which the check data is available, you will find the website direction. Product manual download service Instrumentation ALS Instruments instruction manual https://www.als-japan.com/support-instrument-manual.html Manual download link frontpage --> Support --> Instrument Manual Electrodes ALS support product manual https://www.als-japan.com/support-product-manual.html Manual download link frontpage --> Support --> Products Manual ALS product manual is available for download
    [Show full text]
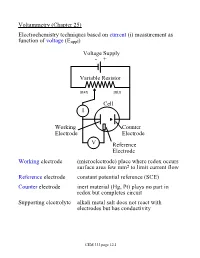
  • Voltammetry (Chapter 25) Electrochemistry Techniques Based on Current (I) Measurement As Function of Voltage (Eappl)
    Voltammetry (Chapter 25) Electrochemistry techniques based on current (i) measurement as function of voltage (Eappl) Voltage Supply - + Variable Resistor max min Cell I Working Counter Electrode Electrode V Reference Electrode Working electrode (microelectrode) place where redox occurs surface area few mm2 to limit current flow Reference electrode constant potential reference (SCE) Counter electrode inert material (Hg, Pt) plays no part in redox but completes circuit Supporting electrolyte alkali metal salt does not react with electrodes but has conductivity CEM 333 page 12.1 Why not use 2 electrodes? OK in potentiometry - very small currents. Now, want to measure current (larger=better) but • potential drops when current is taken from electrode (IR drop) • must minimize current withdrawn from reference electrode surface Potentiostat (voltage source) drives cell • supplies whatever voltage needed between working and counter electrodes to maintain specific voltage between working and reference electrode NOTE: • Almost all current carried between working and counter electrodes • Voltage measured between working and reference electrodes • Analyte dissolved in cell not at electrode surface! CEM 333 page 12.2 Excitation signals (Fig 25-2) CEM 333 page 12.3 Microelectrodes C, Au, Pt, Hg each useful in certain solutions/voltage ranges Fig 25-4 At -ve limit, oxidation of water + - 2H2O ® 4H + O2(g) + 4e At +ve limit, reduction of water - - 2H2O + 2e ® H2 + 2OH CEM 333 page 12.4 Varies with material/solution due to different overpotentials Overpotential
    [Show full text]
  • Liquid Interfaces in Microfluidic Systems
    Institute of Physical Chemistry Polish Academy of Sciences Kasprzaka 44/52 01-224 Warsaw, Poland PHD THESIS ELECTROCHEMICAL PROCESSES AT LIQUID|LIQUID INTERFACES IN MICROFLUIDIC SYSTEMS Dawid Kałuża Supervisor: dr hab. Martin Jönsson-Niedziółka, prof. IChF PAN This dissertation was prepared within the International PhD Studies at the Institute of Physical Chemistry of the Polish Academy of Sciences in Warsaw Warsaw, July 2016 ACKNOWLEDGEMENTS ACKNOWLEDGEMENTS Firstly, I would like to express my special appreciation to my promotor, dr hab. Martin Jönsson-Niedziółka, for supporting me during these five years. Thank you for encouraging my research and for allowing me to grow as a research scientist. I would also like to thank prof. dr hab. Marcin Opałło for help me to start my PhD studies. I am grateful to dr inż Wojciech Adamiak who has introduced me in electrochemistry at the liquid|liquid interfaces and also for being valuable source of support. I am grateful to dr inż. Ewa Roźniecka who has helped me to make a first step in microfluidic research. I am also grateful to prof. Frank Marken for fruitful collaboration and opportunity to work in his research group together with PhD Sunyhik Ahn. Many thanks to all my colleagues from Department of Electrode Processes IPC PAS for everyday nice atmosphere at the work. Finally, I would like to thank my wife and my family for the understanding and constant support. I THE WORK WAS SUPPORTED BY: - the project DEC-2011/01/D/ST4/04182 financed by the Polish National Science Centre - the project NOBLESSE FP7-REGPOT-CT-2011-285949-NOBLESSE financed within the Seventh Framework Programme of the European Union II STRESZCZENIE STRESZCZENIE Celem naukowym niniejszej rozprawy doktorskiej jest zbadanie i zrozumienie podstawowych procesów elektrochemicznych zachodzących na granicy faz ciecz|ciecz w układach mikroprzepływowych.
    [Show full text]
  • Double Potential Step Chronoamperometry at a Microband
    Double Potential Step Chronoamperometry at a Microband Electrode: Theory and Experiment Edward O. Barnes, Linhongjia Xiong, Kristopher R. Ward and Richard G. Compton* *Corresponding author Department of Chemistry, Physical and Theoretical Chemistry Laboratory, Oxford University, South Parks Road, Oxford, OX1 3QZ, United Kingdom. Fax: +44 (0) 1865 275410; Tel: +44 (0) 1865 275413. Email: [email protected] NOTICE: this is the authors version of a work that was accepted for publication in The Journal of Electroanalytical Chemistry. Changes resulting from the publishing process, such as peer review, editing, corrections, structural formatting, and other quality control mechanisms may not be reflected in this document. Changes may have been made to this work since it was submitted for publication. A definitive version was subsequently published in The Journal of Electroanalytical Chemistry, DOI 10.1016/j.jelechem.2013.05.002. arXiv:1305.4773v1 [physics.chem-ph] 21 May 2013 1 Abstract Numerical simulation is used to characterise double potential step chronoamperometry at a microband electrode for a simple redox process, A + e− ⇋ B, under conditions of full support such that diffusion is the only active form of mass transport. The method is shown to be highly sensitive for the measurement of the diffusion coefficients of both A and B, and is applied to the one electron oxidation of decamethylferrocene (DMFc), DMFc e− ⇋ DMFc+, in the − room temperature ionic liquid 1-propyl-3-methylimidazolium bistrifluoromethylsulfonylimide. Theory and experiment are seen to be in excellent agreement and the following values of the −7 2 −1 diffusion coefficients were measured at 298 K: DDMFc = 2.50 10 cm s and D + = × DMFc 9.50 10−8 cm2 s−1.
    [Show full text]
  • For Peer Review Only
    IUPAC Terminology of electrochemical methods of analysis Journal: Pure and Applied Chemistry ManuscriptFor ID PeerPAC-REC-18-01-09.R2 Review Only Manuscript Type: Recommendation Date Submitted by the 27-Feb-2019 Author: Complete List of Authors: Pingarron, José; Complutense University of Madrid, Department of Analytical Chemistry Labuda, Jan; Slovak University of Technology, Department of Analytical Chemistry Barek, Jiří ; Charles University, Faculty of Science, Department of Analytical Chemistry Brett, Christopher; Universidade de Coimbra, Departamento de Química Camões, Maria; Universidade de Lisboa, Centro de Química Estrutural Fojta, Miroslav; Akademie ved Ceské Republiky, Institute of Biophysics Hibbert, David; University of New South Wales, School of Chemistry electoanalytical chemistry, electrodes, potentiometry, amperometry, Keywords: voltammetry, coulometry, electrogravimetry, conductometry, impedimetry, spectroelectrochemistry Author-Supplied Keywords: P.O. 13757, Research Triangle Park, NC (919) 485-8700 Page 1 of 62 IUPAC 1 2 3 4 IUPAC Provisional Recommendation 5 6 7 José M. Pingarrón1, Ján Labuda2, Jiří Barek3, Christopher M.A. Brett4, Maria Filomena 8 Camões5, Miroslav Fojta6, D. Brynn Hibbert7*. 9 10 11 Terminology of electrochemical methods of analysis (IUPAC 12 Recommendations 201x) 13 14 15 16 Abstract: Recommendations are given concerning the terminology of methods used in 17 electroanalytical chemistry.For PeerFundamental Review terms in electrochemistry Only are reproduced from 18 previous PAC Recommendations, and
    [Show full text]
  • Liquid Chromatography Electrochemical Determination of Nicotine in Third-Hand Smoke
    Liquid Chromatography Electrochemical Determination of Nicotine in Third-Hand Smoke Xianglu Peng, Danielle Giltrow, Paul Bowdler and Kevin C. Honeychurch* Centre for Research in Biosciences, Faculty of Health & Life Sciences, University of the West of England, Frenchay Campus, Coldharbour Lane, Bristol, BS16 1QY, UK, *[email protected] Abstract Third-hand smoke (THS) can be defined as the contamination of surfaces by second-hand smoke. This residue can form further pollutants which can be re-suspended in dust or be re-emitted into the gas phase. THS is a complex mixture and as a result studies have focused on nicotine as a marker of THS, it being the most abundant and indicative organic compound deposited. In this present study, the extraction of dust wipe samples and the subsequent chromatographic conditions required for the separation of nicotine by liquid chromatography with electrochemical detection were investigated and optimised. The optimum chromatographic conditions were identified as a 150 mm x 4.6 mm, 5 µm C18 column with a mobile phase consisting of 65 % methanol, 35 % pH 8 20 mM phosphate buffer. Hydrodynamic voltammetry was used to optimise the applied potential which was identified to be +1.8 V (vs. stainless steel). Under these conditions, a linear range for nicotine of 13 to 3240 µg/L (0.26 ng – 65 ng on column) was obtained, with a detection limit of 3.0 µg/L (0.06 ng on column) based on a signal-to-noise ratio of three. Dust wipe samples were extracted in methanol with the aid of sonication. Mean recoveries of 98.4 % (% CV = 7.8 %) were found for dust wipe samples spiked with 6.50 µg of nicotine.
    [Show full text]
  • Body-Fluid Diagnostics in Microliter Samples
    BODY-FLUID DIAGNOSTICS IN MICROLITER SAMPLES by GAUTAM N. SHETTY Submitted in partial fulfillment of requirements for the degree of Doctor of Philosophy Thesis Advisor: Dr. Miklós Gratzl Co-advisor: Dr. Koji Tohda Department of Biomedical Engineering CASE WESTERN RESERVE UNIVERSITY May, 2006 CASE WESTERN RESERVE UNIVERSITY SCHOOL OF GRADUATE STUDIES We hereby approve the thesis/dissertation of Gautam N. Shetty . candidate for the Ph. D. degree *. (signed) Miklós Gratzl (chair of the committee) Koji Tohda Barry Miller Clive. R. Hamlin Mark D. Pagel (date) 01/26/06 *We also certify that written approval has been obtained for any proprietary material contained within. I grant to Case Western Reserve University the right to use this work, irrespective of any copyright, for the University’s own purposes without cost to the University or to its students, agents and employees. I further agree that the University may reproduce and provide single copies of the work, in any format other than in or from microforms, to the public for the cost of reproduction. Gautam N. Shetty . (sign) To my hardworking parents iv TABLE OF CONTENTS List of figures…………………………………………………………………………….vii List of tables………………………………….……………………………………….......ix Acknowledgements……………………………………………………………………......x List of Abbreviations……………………………………………………………………..xi Abstract…………………………………………………………………………………..xii Introduction: Significance, hypotheses and specific aims………………………………...1 Part I Optimization of RSS system parameters Chapter 1 Hydrodynamic Electrochemistry in 20 μL drops in
    [Show full text]
  • Hydrodynamically Modulated Voltammetry in Microreactors
    Hydrodynamically Modulated Voltammetry in Microreactors Luwen Meng Department of Chemical Engineering and Biotechnology University of Cambridge This dissertation is submitted for the degree of Doctor of Philosophy Lucy Cavendish College September 2018 Abstract Hydrodynamically modulated voltammetry in microreactors Luwen Meng This thesis describes modulated methods using both voltammetric and microfluidic perturbations to study mechanisms of electrolysis reactions. The initial chapters provide an overview of applications and research development in the fields of micro-engineering and electrochemistry, including microfabrication methodology, electrochemical detection techniques and analysis methods. Some typical electrochemical reactions have been studied for different kinds of industrial applications. Also hydrodynamic modulation methods have been investigated. The result chapters begin in Chapter 3 with detailed investigation of various electrochemical reactions by using cyclic voltammetry (CV) and large amplitude Fourier transformed alternating current voltammetry (FTACV) under microfluidic conditions. Single electron transfer reactions with different kinetics were studied first by using potassium ferrocyanide and ferrocenecarboxylic acid (FCA). Dual electron transfer reactions with different pathways were investigated by using 2,5-dihydroxybenzoic acid for one step oxidation and N,N,N’,N’- tetramethyl-para-phenylene-diamine (TMPD) for two consecutive one-electron step oxidation. An irreversible reaction was explored by using borohydride solution. Examples of 4- homogeneous reaction mechanisms were studied by using the combinations of Fe(CN)6 /L- cysteine or TMPD/ascorbic acid. The current response of all the electrolysis reactions except single electron transfer reactions was first reported under microfluidic conditions with FTACV, which has shown sensitive with the change of volume flow rates and the substrate concentrations when homogeneous reactions are involved.
    [Show full text]