Aim: How Do We Find the Solution to a Differential Equation Graphically Using the Slope Field

Aim: How do we find the solution to a differential equation graphically using the slope field?

Objectives: to know that slope fields approximate the general solutions, to sketch selected values of slope field, to sketch the particular solution curve.

Grouping: students are given opportunity to work in cooperative setting during this class. Time is purposely set aside for students to work collaboratively on at least one set of exercise problems. During this time, students are encouraged to explain concepts and materials and solutions to each other. Furthermore, students get to present their solutions on the board.

Differentiated instruction: all students are held to the highest standard. However the students that are not performing well are grouped with students that are excelling to serve as study partners. Teacher will informally assess their understanding by asking them questions to ensure that they are keeping up.

Assessment: Class is given multiple occasions to work individually and in groups. Teacher circulates the room to assist and also assess student understanding. Furthermore, students are encouraged to explain work to each other. This is another opportunity for teacher to assess student understanding. Lastly, when lesson is finished, students are grouped for class work, questions that are designed as exit slip problems.

Homework Review (10 minutes): Students are assigned problems to present on board. Students will also answer questions. Teacher can go over a problem if no one in class could explain it

Lesson Development: It is often impossible to find the solution to a differential equation. However for first-order differential equations, if we are able to isolate y ' , then its graphical solution is almost the same as if we take y ' and graph the slope at each point. Each curve represents a particular curve. All together, this is the general solution. [15 min]

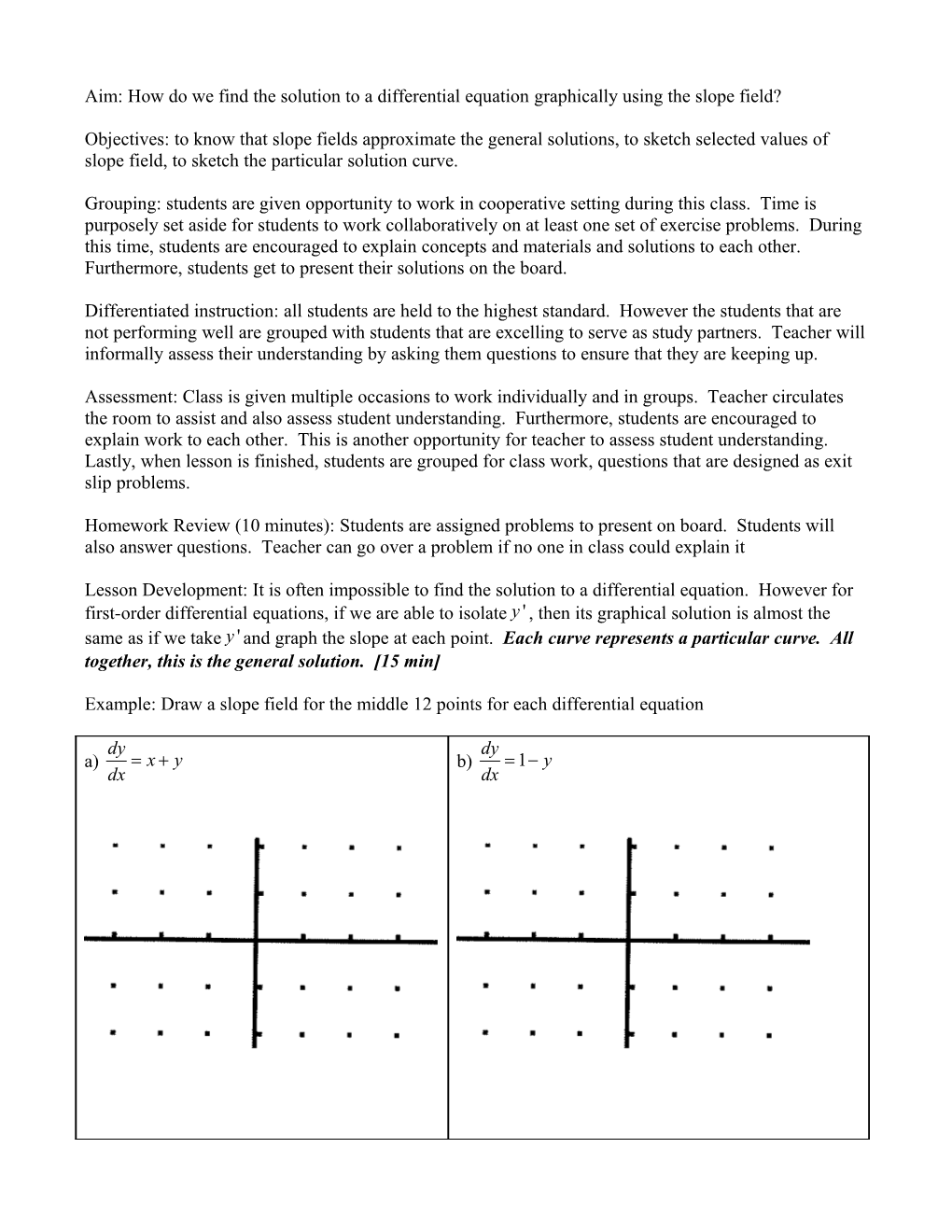
Example: Draw a slope field for the middle 12 points for each differential equation

dy dy a) =x + y b) =1 - y dx dx EX1: Draw a slope field for the middle 12 points for each differential equation [12 min]

dy y f) y'= 2 x + y (1, 1) e) = - dx x

Further development: Understanding the general and particular solution through slope fields. [10 min] dy The differential equation =x + ln y has the slope field shown. Recall that a general solution contains dx a constant C. C can be any value and therefore the general solution has infinitely many solutions. Graphically, the slope fields represent the general solution. The particular solution has a known value for C. So any curve is the particular solution. For example: : sketch a solution curve corresponding to each initial condition, (0, 1) and (-1.5, -0.5) On the AP Exam, it’s very typical to be asked to match a slope field with a particular first order differential equation.

Example: Match the slope fields with their differential equations dy 1 dy dy x I) =x +1 II) =x - y III) = y IV) y ' = - dx 2 dx dx y Name:______HW#79 Match the slope fields with their differential equation

Aim: How do we find the solution to a differential equation graphically using the slope field?

Example: Draw a slope field for the middle 12 points for each differential equation

dy dy a) =x + y b) =1 - y dx dx

EX1: Draw a slope field for the middle 12 points for each differential equation [12 min]

dy y f) y'= 2 x + y (1, 1) e) = - dx x

Further development: Understanding the general and particular solution through slope fields. [10 min] dy The differential equation =x + ln y has the slope field shown. Recall that a general solution contains dx a constant C. C can be any value and therefore the general solution has infinitely many solutions. Graphically, the slope fields represent the general solution. The particular solution has a known value for C. So any curve is the particular solution. For example: : sketch a solution curve corresponding to each initial condition, (0, 1) and (-1.5, -0.5) On the AP Exam, it’s very typical to be asked to match a slope field with a particular first order differential equation.

Example: Match the slope fields with their differential equations dy 1 dy dy x I) =x +1 II) =x - y III) = y IV) y ' = - dx 2 dx dx y