DOCSLIB.ORG

Nature and Reactivity of Oxygen and Hydroxide on Metal Surfaces

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Nature and Reactivity of Oxygen and Hydroxide on Metal Surfaces Nature and Reactivity of Oxygen and Hydroxide on Metal Surfaces A Dissertation Presented to the faculty of the School of Engineering and Applied Science University of Virginia In Partial Fulfillment of the requirements for the Degree Doctor of Philosophy in Chemical Engineering by David Douglas Hibbitts August 2012 2 3 Abstract The catalytic oxidation of hydrocarbons and oxygenates used in the conversion of petroleum and biomass to chemicals and fuels results in formation of surface oxygen intermediates, namely chemisorbed oxygen (O*) and hydroxide (OH*) that can alter the reaction mechanism and control the overall catalytic activity and selectivity. The role of these intermediates and their influence on bond activation depends upon the nature of the metal that is used to carry out catalytic transformations, the specific reaction and the coverage of the adsorbate on the surface. For instance, O* or OH* can act as a Brønsted base reducing the barrier for O-H or C-H activation of alkanes or alcohols through H-abstraction mechanisms. Another example is when a bimetallic alloy is composed of a noble metal and an oxophilic metal, in which OH* bound to the oxophilic metal can act as a Brønsted acid that can catalyze dehydration and hydrogenolysis reactions. On coinage (group IB) metals, the binding energy of O* or OH* is very weak compared to the binding energy on platinum group metals. Furthermore, the charge on the oxygen atom is more negative when O* or OH* is bound to coinage metals than when it’s bound to platinum group metals as there is significant charge transfer from the filled d- band to the oxygen. The weak binding energy and increased charge on the oxygen enable O* or OH* to act as a Brønsted base under a wide range of conditions, thus allowing for the H- abstraction of mildly acidic O-H bonds in alcohols and even non-acidic C-H bonds, such as those found in alkanes. On platinum group metals, O* binds too strongly to the metal surface and is not basic enough, even at the bridge site, to help activate the C-H bonds of alkanes or alcohols. At higher coverages, the O* binding energy decreases, which leads to a greater basicity on the O* (reducing the barrier for O*-assisted C-H activation of methane). However, the O*- assisted activation does have a lower barrier for O-H activations, such as the initial 4 activation of alcohols. For OH*-assisted R-H activation, the activation barriers are lower than the O*-assisted barriers for all metals except Cu and Ag. During alcohol oxidation at high pH, the presence of hydroxide, in solution and adsorbed on the surface, can act as a base to catalyze the initial deprotonation of the alcohol, the hydride elimination of the alkoxide (on the surface) and the nucleophilic addition to the aldehyde, leading to the acid product. As the pH of the system decreases, the rate decreases until a point when a change in the mechanism occurs, in which direct C-H activation of the αC-H bond or O*-assisted O-H activation of the hydroxyl group takes over (depending on the coverage of O*). During the hydrogenolysis of alcohols or cyclic ethers, noble metal catalysts (such as Rh or Pt) are promoted with partially reduced oxides of oxophilic metals (such as MoOx or ReOx). These partially reduced oxides hydroxylate in the presence of water, generating a OH* intermediate strongly bound to the oxophilic metal center, thus resulting in a Brønsted acid site. The acidity of such sites was studied for a wide range of alloys, to determine which combinations might produce acidic OH*. Further investigations studied the effect of the position and form of the alloy as well as the relationship between the acidity and the binding energy of O*, the covalent strength of the O-H bond and the binding energy of ammonia. The results indicate that as the binding energy of O* becomes stronger the strength of the O-H bond decreases thus increasing the acidity of the OH*. The binding energy of ammonia increases with increasing acidity non-linearly. Through these studies, a set of rules can be established to determine the conditions for O* or OH* to act as a base or OH* as an acid when adsorbed on a metal surface (or alloy). 5 Contents Abstract ............................................................................................................................................................................................ 3 Table of Contents ....................................................................................................................................................................... 5 List of Tables ................................................................................................................................................................................. 6 List of Figures ............................................................................................................................................................................... 8 List of Symbols .......................................................................................................................................................................... 12 Preface ........................................................................................................................................................................................... 13 Chapter 1 – Nature of O* and OH* on Metal Surfaces at Various Coverages ......................... 16 Binding State of O* and OH* on Closed-Packed and (100) Transition Metal Surfaces .................................... 17 Hydrogen Bonding of O* on Closed-Packed Transition Metal Surfaces ................................................................. 34 Nature of O* and OH* at Higher Coverages on (111) Surfaces ................................................................................. 46 Chapter 2 – Aqueous-Phase Oxidation of Alcohols over Au, Pt and Pd Catalysts ............. 53 Reactivity of the Gold/Water Interface during Selective Oxidation Catalysis ..................................................... 54 Influence of Oxygen and Alkalinity during Selective Oxidation of Ethanol over Pd Catalysts ...................... 64 Chapter 3 – Effect of O* and OH* on C-H and O-H Bond Activations ............................................ 88 Methane Activation over Clean and Oxygen-Covered Transition Metal Surfaces .............................................. 89 Evaluation of the Brønsted Basicity of O* and OH* on Transition Metal Surfaces ......................................... 107 Chapter 4 – Hydrogenolysis of Polyols and Cyclic Ethers over Bimetallic Alloys .......... 131 Selective Hydrogenolysis of Polyols and Cyclic Ethers over Bifunctional Surface Sites on Rhodium- Rhenium Catalysts ................................................................................................................................................................... 132 Acidity of Hydroxides on Alloys of Noble Metals and Oxophilic Oxide Promoters such as Rh-ReOx ........ 138 Summary and Recommendations for Future Work .............................................................................. 156 References............................................................................................................................................................ 160 6 List of Tables Table 1.1. Binding Energy of O* on Various Transition Metals and Unit Cell Sizes. ..................................... 19 Table 1.2. Charge Transfer to O* on Closed-Packed 3x3 Transition Metal Surfaces. .................................. 21 Table 1.3. Binding Energy of O* on 3x3 Closed-Packed Surfaces of Various Transition Metals and Binding Modes. ............................................................................................................................................................................. 23 Table 1.4. Charge Distribution of O* Bound on a 3x3 Closed-Packed Metal Surface of Various Metals and Binding Modes. .................................................................................................................................................................... 25 Table 1.5. Binding Energy of O* on 3x3 (100) Surfaces of Various Transition Metals and Binding Modes. ............................................................................................................................................................................................... 27 Table 1.6. Binding Energy of OH* on 3x3 Closed-Packed Surfaces of Various Transition Metals and Binding Modes. ...........................................................................................................................................................29 Table 1.7. Charge Distribution of OH* Bound on Various Transition Metals and Binding Modes. ........ 31 Table 1.8. Binding Energy of OH* on (100) Surfaces of Various Transition Metals and Binding Modes. ............................................................................................................................................................................................... 32 Table 1.9. Average Hydrogen Bond Interactions between H2O and O* on All Studied Transition Metals. ............................................................................................................................................................................................... 38 Table 1.10. Average Hydrogen Bond Interactions between H2O and O* on Coinage Metals. ................. 39 Table 1.11. Average Hydrogen Bond Interactions
Load more

Recommended publications
  • Aldehydes and Ketones
    Organic Lecture Series Aldehydes And Ketones Chap 16 111 Organic Lecture Series IUPAC names • the parent alkane is the longest chain that contains the carbonyl group • for ketones, change the suffix -e to -one • number the chain to give C=O the smaller number • the IUPAC retains the common names acetone, acetophenone, and benzophenone O O O O Propanone Acetophenone Benzophenone 1-Phenyl-1-pentanone (Acetone) Commit to memory 222 Organic Lecture Series Common Names – for an aldehyde , the common name is derived from the common name of the corresponding carboxylic acid O O O O HCH HCOH CH3 CH CH3 COH Formaldehyde Formic acid Acetaldehyde Acetic acid – for a ketone , name the two alkyl or aryl groups bonded to the carbonyl carbon and add the word ketone O O O Ethyl isopropyl ketone Diethyl ketone Dicyclohexyl ketone 333 Organic Lecture Series Drawing Mechanisms • Use double-barbed arrows to indicate the flow of pairs of e - • Draw the arrow from higher e - density to lower e - density i.e. from the nucleophile to the electrophile • Removing e - density from an atom will create a formal + charge • Adding e - density to an atom will create a formal - charge • Proton transfer is fast (kinetics) and usually reversible 444 Organic Lecture Series Reaction Themes One of the most common reaction themes of a carbonyl group is addition of a nucleophile to form a tetrahedral carbonyl addition compound (intermediate). - R O Nu - + C O Nu C R R R Tetrahedral carbonyl addition compound 555 Reaction Themes Organic Lecture Series A second common theme is
    [Show full text]
  • Organic Chemistry/Fourth Edition: E-Text
    CHAPTER 17 ALDEHYDES AND KETONES: NUCLEOPHILIC ADDITION TO THE CARBONYL GROUP O X ldehydes and ketones contain an acyl group RC± bonded either to hydrogen or Ato another carbon. O O O X X X HCH RCH RCRЈ Formaldehyde Aldehyde Ketone Although the present chapter includes the usual collection of topics designed to acquaint us with a particular class of compounds, its central theme is a fundamental reaction type, nucleophilic addition to carbonyl groups. The principles of nucleophilic addition to alde- hydes and ketones developed here will be seen to have broad applicability in later chap- ters when transformations of various derivatives of carboxylic acids are discussed. 17.1 NOMENCLATURE O X The longest continuous chain that contains the ±CH group provides the base name for aldehydes. The -e ending of the corresponding alkane name is replaced by -al, and sub- stituents are specified in the usual way. It is not necessary to specify the location of O X the ±CH group in the name, since the chain must be numbered by starting with this group as C-1. The suffix -dial is added to the appropriate alkane name when the com- pound contains two aldehyde functions.* * The -e ending of an alkane name is dropped before a suffix beginning with a vowel (-al) and retained be- fore one beginning with a consonant (-dial). 654 Back Forward Main Menu TOC Study Guide TOC Student OLC MHHE Website 17.1 Nomenclature 655 CH3 O O O O CH3CCH2CH2CH CH2 CHCH2CH2CH2CH HCCHCH CH3 4,4-Dimethylpentanal 5-Hexenal 2-Phenylpropanedial When a formyl group (±CHœO) is attached to a ring, the ring name is followed by the suffix -carbaldehyde.
    [Show full text]
  • Cu(II) Catalyzed Unsymmetrical Di-Oxidation of Gem- Difluoroalkenes to Generate Α,Α-Difluorinated-Α-Phenoxyketones, an Unstudied Substructure
    Cu(II) Catalyzed Unsymmetrical Di-oxidation of gem- Difluoroalkenes to Generate α,α-Difluorinated-α-Phenoxyketones, an Unstudied Substructure Suvajit Koley, [a] Kaylee T. Cayton, [b] Gisela A. González-Montiel,[b] M. Ramu Yadav,[c] Douglas L. Orsi,[d] Paul Ha-Yeon Cheong,*[b] and Ryan A. Altman*[a] [a] Dr. S. Koley, Dr. R. A. Altman Department of Medicinal Chemistry and Molecular Pharmacology; Department of Chemistry Purdue University West Lafayette, IN 47907 (USA) E-mail: [email protected] [b] K. T. Cayton, G. A. González-Montiel, Dr. P. H.-Y. Cheong Department of Chemistry Oregon State University 153 Gilbert Hall, Corvallis, OR 97331 (USA) [c] Dr. M. R. Yadav Department of Chemistry Indian Institute of Technology Delhi MS-723, Hauz Khas, New Delhi-110016 (India) [d] Dr. D. L. Orsi Broad Institute of Harvard and MIT Cambridge, MA 02142 (USA) Supporting information for this article is given via a link at the end of the document. Abstract: A Cu-based catalyst system convergently couples gem- conformers versus the parent alkyl-aryl ethers that preferentially difluoroalkenes with phenols under aerobic conditions to deliver α,α- reside in the plane of the arene,[23] and versus trifluoromethyl-aryl difluorinated-α-phenoxy ketones, an unstudied hybrid fluorinated ethers that reside orthogonally to the plane of the arene.[24] functional group. Composed of α,α-difluorinated ketone and α,α- Interestingly, despite the individual significance of the α,α- difluorinated ether moieties, these have only once been previously difluoroketone and α,α-difluoroalkyl ethers components, the reported as a synthetic intermediate en route to pharmacologically hybrid α,α-difluorinated-α-phenoxy-ketone functional group has active compounds.
    [Show full text]
  • Hydrogen Peroxide Production Via a Redox Reaction of N,N&
    ChemComm View Article Online COMMUNICATION View Journal | View Issue Hydrogen peroxide production via a redox reaction of N,N0-dimethyl-2,6-diaza-9,10- Cite this: Chem. Commun., 2018, 54, 11204 anthraquinonediium by addition of bisulfite† Received 11th July 2018, Accepted 13th September 2018 Igor V. Kolesnichenko, P. Rogelio Escamilla, Jason A. Michael, Vincent M. Lynch, David A. Vanden Bout * and Eric V. Anslyn * DOI: 10.1039/c8cc05548c rsc.li/chemcomm We demonstrate that bisulfite can be used for reduction of a highly electrophilic anthraquinone derivative, N,N0-dimethyl-2,6-diaza- 9,10-anthraquinonediium (DAAQ), and subsequent autoxidation generates an equivalent of hydrogen peroxide. The mechanism for DAAQ reduction by bisulfite, DAAQ electrochemistry, and use of a simple test strip assay for H2O2, are described. Since the 1940s the most widely used industrial method of production of hydrogen peroxide (H2O2) has been via the catalytic reduction of a 2-substituted anthraquinone, followed by autoxidation in the presence of molecular oxygen. This method, known as the Riedl–Pfleiderer1 process, has seen several improvements2–10 and is very high yielding in H O .2–4,11–15 There 2 2 Fig. 1 Structures of relevant anthraquinone derivatives. are a variety of quantitative tests for hydrogen peroxide in aqueous media: electrochemical,16–19 spectroscopic,20,21 and even 22 simple colorimetric test strips. The generation of H2O2 has In 2003 Morgan and coworkers published a spectroscopic been used to quantitate other species when their presence can study of 2,6-diazaanthracene-9,10-dione (DAAD), an anthraqui- Published on 13 September 2018.
    [Show full text]
  • Delft University of Technology Direct Diels-Alder Reactions of Furfural
    Delft University of Technology Direct Diels-Alder reactions of furfural derivatives with maleimides Cioc, Rǎzvan C.; Lutz, Martin; Pidko, Evgeny A.; Crockatt, Marc; Van Der Waal, Jan C.; Bruijnincx, Pieter C.A. DOI 10.1039/d0gc03558k Publication date 2021 Document Version Final published version Published in Green Chemistry Citation (APA) Cioc, R. C., Lutz, M., Pidko, E. A., Crockatt, M., Van Der Waal, J. C., & Bruijnincx, P. C. A. (2021). Direct Diels-Alder reactions of furfural derivatives with maleimides. Green Chemistry, 23(1), 367-373. https://doi.org/10.1039/d0gc03558k Important note To cite this publication, please use the final published version (if applicable). Please check the document version above. Copyright Other than for strictly personal use, it is not permitted to download, forward or distribute the text or part of it, without the consent of the author(s) and/or copyright holder(s), unless the work is under an open content license such as Creative Commons. Takedown policy Please contact us and provide details if you believe this document breaches copyrights. We will remove access to the work immediately and investigate your claim. This work is downloaded from Delft University of Technology. For technical reasons the number of authors shown on this cover page is limited to a maximum of 10. Green Chemistry View Article Online PAPER View Journal | View Issue Direct Diels–Alder reactions of furfural derivatives with maleimides† Cite this: Green Chem., 2021, 23, 367 Răzvan C. Cioc,a Martin Lutz,b Evgeny A. Pidko, c Marc Crockatt,d Jan C. van der Waald and Pieter C.
    [Show full text]
  • Homogeneously Catalysed Conversion of Aqueous Formaldehyde to H2 and Carbonate
    ARTICLE Received 27 Sep 2016 | Accepted 20 Feb 2017 | Published 28 Apr 2017 DOI: 10.1038/ncomms14990 OPEN Homogeneously catalysed conversion of aqueous formaldehyde to H2 and carbonate M. Trincado1, Vivek Sinha2, Rafael E. Rodriguez-Lugo3, Bruno Pribanic1, Bas de Bruin2 & Hansjo¨rg Gru¨tzmacher1 Small organic molecules provide a promising solution for the requirement to store large amounts of hydrogen in a future hydrogen-based energy system. Herein, we report that diolefin–ruthenium complexes containing the chemically and redox non-innocent ligand trop2dad catalyse the production of H2 from formaldehyde and water in the presence of a base. The process involves the catalytic conversion to carbonate salt using aqueous solutions and is the fastest reported for acceptorless formalin dehydrogenation to date. A mechanism supported by density functional theory calculations postulates protonation of a ruthenium hydride to form a low-valent active species, the reversible uptake of dihydrogen by the ligand and active participation of both the ligand and the metal in substrate activation and dihy- drogen bond formation. 1 Department of Chemistry and Applied Biosciences ETH Zu¨rich, Laboratory of Inorganic Chemistry, Wolfgang Pauli Str. 10, Zu¨rich CH-8093, Switzerland. 2 Supramolecular and Homogeneous Catalysis Group, van ’t Hoff Institute for Molecular Sciences (HIMS), University of Amsterdam, Science Park 904, Amsterdam 1098 XH, The Netherlands. 3 Labotatorio de Quı´mica Bioinorga´nica, Centro de Quı´mica, Instituto Venezolano de Investigaciones Cientı´ficas (IVIC), Caracas 1020-A, Venezuela. Correspondence and requests for materials should be addressed to M.T. (email: [email protected]) or to B.d.B.
    [Show full text]
  • Gas-Phase Water-Mediated Equilibrium Between SPECIAL FEATURE Methylglyoxal and Its Geminal Diol
    Gas-phase water-mediated equilibrium between SPECIAL FEATURE methylglyoxal and its geminal diol Jessica L. Axsona,b, Kaito Takahashic, David O. De Haand, and Veronica Vaidaa,b,1 aDepartment of Chemistry and Biochemistry, and bCooperative Institute for Research in Environmental Sciences, Campus Box 215, University of Colorado, Boulder, CO 80309; cThe Institute of Atomic and Molecular Sciences, P.O. Box 23-166, Taipei, Taiwan 10617, Republic of China; and dDepartment of Chemistry and Biochemistry, University of San Diego, 5998 Alcala Park, San Diego, CA 92110 Edited by Barbara J. Finlayson-Pitts, University of California, Irvine, CA, and approved December 15, 2009 (received for review October 20, 2009) In aqueous solution, aldehydes, and to a lesser extent ketones, mined computationally that the aldehydic C ¼ O is more favor- −1 hydrate to form geminal diols. We investigate the hydration of ably hydrated in solution (ΔG ¼ −1.4 kcal mol ) than the −1 methylglyoxal (MG) in the gas phase, a process not previously ketonic C ¼ O(ΔG ¼þ2.5 kcal mol ) (21). In solution, MG considered to occur in water-restricted environments. In this study, is present primarily as MGD (60% diol to 40% tetrol) with we spectroscopically identified methylglyoxal diol (MGD) and the aldehydic group forming a geminal diol (21, 23). MGD obtained the gas-phase partial pressures of MG and MGD. These has a lower vapor pressure than MG, which allows the molecule results, in conjunction with the relative humidity, were used to ob- to partition more easily into the particle phase, lending to the tain the equilibrium constant, KP, for the water-mediated hydration formation of SOA.
    [Show full text]
  • CHEM 203 Summary of Topics to Be Covered in the Course INDEX A
    CHEM 203 Summary of Topics to be Covered in the Course INDEX A. Introduction p. 3 Lecture 1: Structural theory of organic chemistry p. 3 B. Aspects of the Electronic Theory of Organic Chemistry p. 5 Lecture 2: Electronic theory of organic chemistry p. 5 Lecture 3: Lewis acid-base interactions p. 11 C. Alkenes p. 14 Lecture 4: Bronsted acid-base equilibria, alkenes p. 14 Lecture 5: Electrophilic addition of H–X to alkenes p. 21 Lecture 6: Regioselective addition of H–X to alkenes p. 26 Lecture 7: Regioselective addition of H–X to alkenes, rearrangements p. 31 Lecture 8: Stereochemical aspects of H–X the additions to alkenes p. 35 Lecture 9: Hydration of alkenes p. 39 Lecture 10: Addition of "water-like" molecules to alkenes p. 42 Lecture 11: Halogenation of alkenes & stereochemical aspects p. 45 Lecture 12: Halogenation, halohydrins, stereochemical aspects p. 49 Lecture 13: Ozonolysis of alkenes p. 53 Lecture 14: Osmylation of alkenes p. 58 Lecture 15: Hydroboration of alkenes p. 61 Lecture 16: Hydrogenation of alkenes p. 66 Lecture 17: Radical addition to alkenes - I p. 70 Lecture 18: Radical addition to alkenes - II p. 75 D. Alkynes p. 79 Lecture 19: Chemistry of Alkynes p. 79 E. Alkyl Halides p. 83 Lecture 20: Alkyl halides - halogenation of C–H bonds p. 83 Lecture 21: SN2 reactions - I p. 88 Lecture 22: SN2 reactions - II p. 91 Lecture 23: SN2 vs. elimination reactions p. 94 Lecture 24: E2 reactions p. 98 Lecture 25: SN1 and E1 reactions p. 102 Lecture 26: SET reactions of alkyl halides: organometallics p.
    [Show full text]
  • Geminal Diol of Dihydrolevoglucosenone As a Switchable Hydrotrope: a Continuum of Green Nanostructured Solvents Mario De Bruyn,*,†,‡ Vitaliy L
    This is an open access article published under a Creative Commons Non-Commercial No Derivative Works (CC-BY-NC-ND) Attribution License, which permits copying and redistribution of the article, and creation of adaptations, all for non-commercial purposes. Research Article Cite This: ACS Sustainable Chem. Eng. 2019, 7, 7878−7883 pubs.acs.org/journal/ascecg Geminal Diol of Dihydrolevoglucosenone as a Switchable Hydrotrope: A Continuum of Green Nanostructured Solvents Mario De bruyn,*,†,‡ Vitaliy L. Budarin,§ Antonio Misefari,§ Seishi Shimizu,∥ Heather Fish,∥ Martin Cockett,∥ Andrew J. Hunt,⊥ Heike Hofstetter,# Bert M. Weckhuysen,‡ James H. Clark,§ and Duncan J. Macquarrie§ † Department of Chemical and Biological Engineering, University of Wisconsin-Madison, 1415 Engineering Drive, Madison, Wisconsin 53706, United States ‡ Faculty of Science, Debye Institute for Nanomaterials Science, Utrecht University, Universiteitsweg 99, CG Utrecht 3584, The Netherlands § ∥ Green Chemistry Centre of Excellence, Department of Chemistry, and Department of Chemistry, University of York, York YO10 5DD, United Kingdom ⊥ Materials Chemistry Research Center, Department of Chemistry and Center of Excellence for Innovation in Chemistry, Faculty of Science, Khon Kaen University, Khon Kaen 40002, Thailand # Department of Chemistry, University of Wisconsin-Madison, 1101 University Avenue, Madison, Wisconsin 53706, United States *S Supporting Information ABSTRACT: The addition of water to dihydrolevoglucose- none (Cyrene) creates a solvent mixture with highly unusual properties and the ability to specifically and efficiently solubilize a wide range of organic compounds, notably, aspirin, ibuprofen, salicylic acid, ferulic acid, caffeine, and mandelic acid. The observed solubility enhancement (up to 100-fold) can be explained only by the existence of microenvironments mainly centered on Cyrene’s geminal diol.
    [Show full text]
  • Oxoethyl Flavin Revisited
    2 -Oxoethyl Flavin Revisited Jiˇr´ı Svobodaa, Burkhard K¨oniga, Keyarash Sadeghianb, and Martin Sch¨utzb a Institute of Organic Chemistry, University Regensburg, D-93040 Regensburg, Germany b Institute of Physical and Theoretical Chemistry, University Regensburg, D-93040 Regensburg, Germany Reprint requests to Prof. B. K¨onig. E-mail: [email protected] Z. Naturforsch. 2008, 63b, 47 – 54; received August 3, 2007 The present work investigates the possibility of using 2-oxoethyl flavin (2) as a starting material for the construction of more complicated flavin-based molecules. 2-Oxoethyl flavin (2), prepared by oxidative degradation of commercially available riboflavin 1, is however a rather untypical aldehyde. It prefers the hydrated gem-diol form 4 in aqueous solution. Ab initio electronic structure calculations, carried out at the level of Møller-Plesset perturbation theory of second order (MP2), predict the existence of an intramolecular hydrogen bond between one of the hydroxy groups of the diol and the N1 atom of the flavin skeleton. This result is supported by 1H NMR measurements which indicate an interaction between the hydroxy groups and the conjugated ring system. We postulate that this rather strong intramolecular hydrogen bond is the origin of the enhanced stability of the gem-diol over the aldehyde form 2. Synthetic applicability of 2-oxoethyl flavin 2 is limited by low solubility in most organic sol- vents and sensitivity to basic conditions. The aldehyde functional group is surprisingly reluctant to nucleophilic attack, and several reactions quite typical for aldehydes failed. Nevertheless, reductive amination led to the expected secondary amine 7.
    [Show full text]
  • Accurate Computational Model for the Hydration Extent of Atmospherically Relevant Carbonyls on Aqueous Atmospheric Particles Matthew J
    http://pubs.acs.org/journal/aesccq Article Accurate Computational Model for the Hydration Extent of Atmospherically Relevant Carbonyls on Aqueous Atmospheric Particles Matthew J. Elrod,* Jane A. Sedlak, and He Ren Cite This: ACS Earth Space Chem. 2021, 5, 348−355 Read Online ACCESS Metrics & More Article Recommendations *sı Supporting Information ABSTRACT: The carbonyl hydration equilibria of several atmospherically relevant carbonyl compounds were studied using nuclear magnetic resonance (NMR) spectroscopy and computationally investigated using the MG2MS electronic structure method. The results were used to build an empirically adjusted computational model that resulted in the calculation of free energies of hydration that were accurate to within 1 kcal mol−1. The new model was used to predict the hydration extent of other potentially atmospherically relevant carbonyl compounds for which no experimental data exists. Because the hydration extent of a carbonyl compound dramatically affects its effective volatility and Henry’s law solubility, the more accurate estimates for the extent of carbonyl hydration predicted by this new model will help improve our understanding of which carbonyl compounds are major constituents of aqueous atmospheric particles. KEYWORDS: atmosphere, aerosol, carbonyl, hydration, equilibrium ■ INTRODUCTION Secondary organic aerosol (SOA)1 forms in the atmosphere via gas-particle partitioning. SOA chemical composition can also ff be a ected by in-particle chemical processing of condensed Figure 1. Hydration equilibrium
    [Show full text]
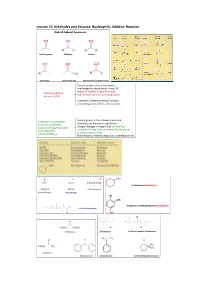
  • Lecture 10 Aldehydes and Ketones: Nucleophilic Addition Reaction Kinds of Carbonyl Compounds
    Lecture 10 Aldehydes and Ketones: Nucleophilic Addition Reaction Kinds of Carbonyl Compounds O O O C C C R H R R' Carbonyl group Aldehyde Ketone O O O C C C R OH R X Acyl group Carboxylic group Derivatives of carboxylic acids The acyl groups in these two families are bonded to substituents (‐Hand–R) that can’t stabilize a negative charge Aldehydes (RCHO) and therefore can’t act as leaving groups. Ketones (R2CO) Aldehydes and ketones behave similarly and undergo many of the same reactions. The acyl groups in the carboxylic acids and Carboxylic acids (RCOOH) derivatives are bonded to substituents Acid chlorides (RCOCl) (oxygen, halogen, nitrogen) that can stabilize Acid anhydrides (RCOOCOR’) a negative charge and can serve as leaving groups Esters (RCOOR’) in substitution reactions. Amides (RCONH2) The chemistry of these compounds is therefore similar. O O O CHO HCH CH3CH ClCH2CH2CH2CH 4 3 2 1 Cyclohexanecarbaldehyde Methanal Ethanal 4‐Chlorobutanal (Formaldehyde) (Acetaldehyd) OH OMe 2 4‐Hydroxy‐3‐methoxybenzenecarbaldehyde 5 3 1 H 7 6 4 4,6‐Dimethylheptanal O CHO Cl 5 3 1 2 3 O 4 7 5 1 6 4 2 C CH3CH2 CH2CH3 O O 3‐Pentanone 2‐Pentanone 4‐Chloro‐6‐methyl‐3‐heptanone 2 1 O CH3 O O C O C C 1 C 2 CH3 CH3CH2 CH3 CH3 2‐butanone Benzophenone Acetophenone 2,2‐Dimethylcyclopentanone O O RC HC Formyl O O An acyl group CH CH CH CH 3 2 2 CH3CH2CH2CHO H O Butanal C O Benzoyl O CH3C CH3CH2CCH3 CH3CH2COCH3 Acetyl 2‐Butanone O Structure of the Carbonyl Group short strong polar + - C O C O or C O electrophilic nucleophilic Na2Cr2O7 KMnO4 OH O CrO3, H2SO4, aceton, 0ºC CH3CHC C(CH2)3CH3 CH3CC C(CH2)3CH3 O OH O Cr(VI), H+ H2O Cr(VI) RCH2OH RCH RCOH RCOH H O O O PCC, CH2Cl2, CH3COONa O O CH2OH CH Ozonolysis Hydration of Terminal Alkyne O HO H HOH, H+, Hg2+ RC CH C C RCCH3 R H Markovnikov rule Friedel‐Crafts Acylation O O 1.
    [Show full text]