1. Williams Products

Supplement A Decision Making

PROBLEMS

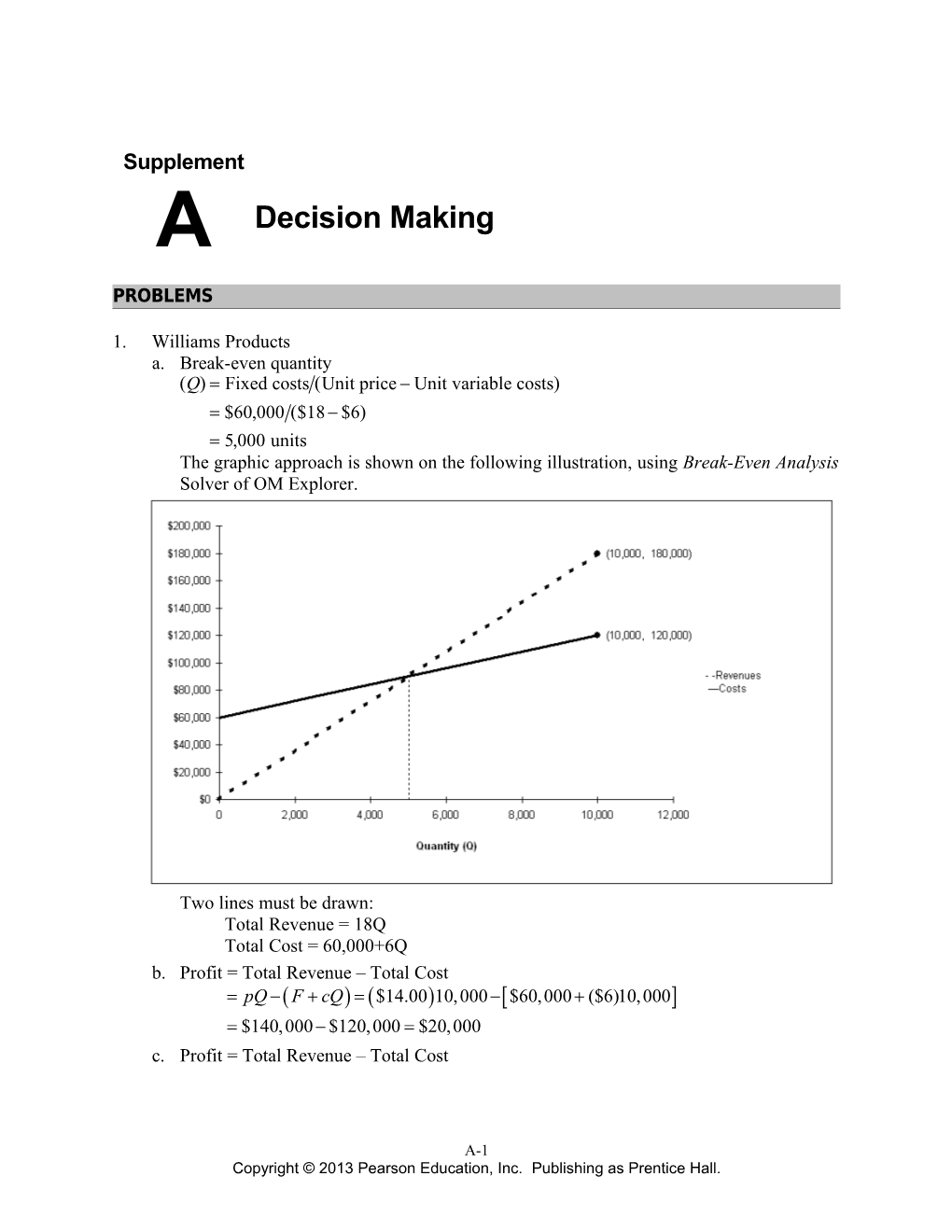
1. Williams Products a. Break-even quantity Q  Fixed costs Unit price  Unit variable costs  $60,000 $18  $6  5,000 units The graphic approach is shown on the following illustration, using Break-Even Analysis Solver of OM Explorer.

Two lines must be drawn: Total Revenue = 18Q Total Cost = 60,000+6Q b. Profit = Total Revenue – Total Cost =pQ -( F + cQ) =($14.00) 10,000 -[ $60,000 + ($6)10,000] =$140,000 - $120,000 = $20,000 c. Profit = Total Revenue – Total Cost

=pQ -( F + cQ) =($12.50) 15,000 -臌轾 $60,000 + ( $6) 15,000 =$187,500 - $150,000 = $37,500 Therefore, the strategy of using a price of $12.50 will result in a greater contribution to profits. d. Williams must also consider how this product fits within her existing product line from the perspective of required technologies and distribution channels. Other marketing, operations, and financial criteria must also be considered.

2. Jennings Company a. Break-even quantity Q Fixed costs Unit price  Unit variable costs $80,000 $22  $18  20,000 units The graphic approach is shown on the following graph created by the Break-Even Analysis Solver.

Two lines are:

Two lines are: Total Revenues:= $22Q Total costs:= $80,000 + 18Q b. In order to calculate the new unit variable cost required to breakeven, use the breakeven equation from part a, but solve for unit variable cost (c).

80,000 =17,500 22 - c 80,000= (22 - c )17,500 80,000= 385,000 - 17,500c c =17.43 Thus the variable cost would have to reduce from $18 per unit to $17.43 per unit.

c. With a one dollar price decrease, the breakeven quantity would be: 80,000 = 26,667 (22- 1) - 18 This quantity exceeds a 50% increase in sales (17,500 x 1.5) = 26,250

Thus, sales would have to increase by 52% (26,667/17,500=1.52) for Jennings to breakeven with a $1 reduction in price.

d. Alternative 1: Sales increase by 30 percent, to 22,750 units (or 17,500 x 1.3). Profit  pQ  F  cQ  $2222,750  $80,000  $1822,750  $11,000 Alternative 2: Cost reduction to 85 percent results in $15.30 (or $18 x 0.85) unit cost. Profit  pQ  F  cQ  $2217,500  $80,000  $15.3017,500  $37,250 Therefore the cost reduction leads to much higher profits in this example.

e. Initial unit profit is $22  $18  $4.00 Alternative 1: $22  $18  $4.00 The percentage change in profit margin is zero. Alternative 2: $22  $15.30  $6.70

The percentage change is [($6.70$4)/4]100 =67.5% increase.

3. Interactive television service F  p  cQ  $15  $1015,000  $75,000

4. Brook Trout Q= F( p - c) p=( F Q) + c =$10,600 800 + $6.70 = $19.95

5. Spartan Castings a. Total cost= Fixed cost + Variable cost TC  F  cQ TC( first process)  $350,000  $50Q TC(second process)  $150,000 $90Q

At the break-even quantity, $350,000  $50Q  $150,000  90Q $200,000  $40Q Q  5000units Beyond 5000 units the first process becomes more attractive.

b. At Q=10,000 units

TC( first process)  $350,000  $50(10,000)  $850,000 TC(second process)  $150,000  $90(10,000)  $1,050,000 The difference in total cost = $1,050,000 - $850,000 = $200,000

6. News clipping service F  F $400,000  $1,300,000 a. Q  m a   227,848 clippings ca  cm $2.25  $6.20 b. Profit  Total Revenue  Total Cost Current (manual) situation:  225,000  $8.00  $400,000  225,000  $6.20 Profit  $5,000 Modernization:  900,000  $4.00  $1,300,000  900,000  $2.25 Profit  $275,000 The clipping service should be modernized. F $1,300,000 c. Q    742,857 clippings p c $4.00  $2.25

7. Hahn Manufacturing a. Total cost of buying 750 units from the supplier:

TCb  $1,500 unit750 units  $1,125,000 Total cost of making 750 units in-house:

TCm  $1,100 unit $300 unit750 units  $40,000  $1,090,000 Therefore Hahn should make the components in-house, saving $35,000 per year. b. At the break-even quantity, the total cost of the two alternatives will be equal: $1,500Q  $40,000  $1,400Q 100Q  $40,000 Q  400 units

c. If the decision is to “buy,” Hahn may get a quantity discount from the supplier (we would be ordering 750 per year instead of the current 150 per year). Just a $50 per unit quantity discount would make the “buy” alternative more attractive than the “make” alternative. Because the component is a key item, Hahn should check the reliability of the supplier and of their own processes. Reliability may argue for the “make” decision.

8 Current Profit=( Price- Variable cost)( Annual Volume) - Annual Fixed Costs . =($10.00 - $5.00)( 30,000) - ( $140,000) = $10,000 a. Profit with new equipment  $10.00  $6.0050,000  $200,000  $0 Because the profit decreases, Techno should not buy the new equipment. b. Profit with new equipment  $11.00  $6.0045,000  $200,000  $25,000 Because the profit increases, Techno should buy the new equipment if they also raise the selling price.

9. This problem is a thinly disguised portrayal of an actual situation faced by Tri-State G&T Association, Inc. of Thornton, Colorado, and which is common to many other REA Utilities. However the costs, prices, and demands stated in the problem are fictional. F a. Q = p- c F $82,500,000 p= + c = +$25 = $107.5 per MWH Q 1,000,000 b. Profit (or loss)  Total Revenue – Total Cost  1,000,000  95%$107.5  $82,500,000  1,000,000  95%$25  $102,125,000  $106,250,000 Loss  $4,125,000 In order to break even, the price would have to be raised to 骣 $4,125,000 琪$107.5+ = $111.842 , assuming even more conservation would not occur 桫 950,000 at this higher price.

Tri-County G&T: Problem 9 Problem 11 140 120 100 Total Costs 80 60 Total Revenue 40

0.25 0.50 0.75 1.00 1.25 Volume, ( Q , in thousands of MWH)

10. Earthquake ... Build or Buy. This problem is related to problem 9.

Build: F1  Qc1  $10,000,000  150,000MWH  $35  $15,250,000 Buy: F2  Qc2  $0  150,000MWH  $75  $11,250,000 It would be less costly for Boulder to buy power from Tri-County. Note that Boulder enjoys a lower price ($75) than Tri-County charges its own REA customers ($107.50).

11. Tri-County G&T continued. This problem builds on problems 9 and 10 to show that Tri-County’s REA customers also benefit from the bargain arrangement with Boulder. Contribution from sales to Boulder  Qp  c  150,000$75  $25  $7,500,000 Remaining fixed costs to cover  $82,500,000  $7,500,000  $75,000,000 F Q  p  c F $75,000,000 p   c   $25  $100 per MWH Q 1,000,000 Note that selling power to Boulder at a reduced price also reduces the price to the REA customers. However, it may be difficult to persuade REAs that selling electricity to city slickers below “cost” also benefits rural customers.

12. Forsite Company a. Say that each criterion (arbitrarily) receives 20 points: Service Calculation Total Score A 200.6  200.7  200.4  201.0  200.2 = 58 B 200.8  200.3  200.7  200.4  201.0 = 64 C 200.3  200.9  200.5  200.6  200.5 = 56 The best alternative is service B and the worst is service C. This relationship holds as long as any arbitrary weight is equally applied to all performance criteria. b. Let x  point allocation to criteria 1, 3, 4, and 5 2x  point allocation to criteria 2 ROI x  2x  x  x  x  100 points 6x  100 points x  16.7 points Product Calculation Total Score A 16.70.6  33.30.7 16.70.4 16.71.0 16.70.2 = 60.0 B 16.70.8  33.30.3 16.70.7 16.70.4 16.71.0 = 58.4 C 16.7 0.3  33.3 0.9  16.7 0.5  16.7 0.6  16.7 0.5 = 61.7 The rank order of the services has changed to C, A, B.

13. Five new suppliers a. Let x  point allocation to criteria 2 and 3 4x  point allocation to criterion 1 4x  point allocation to criterion 4 4x  x  x  4x  100 points 10x  100 points x  10 points Supplier Calculation Total Score A 408 103 109  407 = 720 B 407 108 105  406 = 650 C 403 104 107  409 = 590 D 406 107 106  402 = 450 E 409 107 105  407 = 760

The threshold is 0.7 1040 10 10  40  700

Because Supplier A and Supplier E score greater than 700, they should be considered. b. If the factors are equally weighted:

Supplier Calculation Total Score A 25(8+3+9+7) = 675 B 25(7+8+5+6) = 650 C 25(3+4+7+9) = 575 D 25(6+7+6+2) = 525 E 25(9+7+5+7) = 700

The threshold is 0.7 1040 10 10  40  700

Because no supplier’s score is greater than 700, none should be considered. Stay with the current suppliers, which presumably have scores greater than 700.

14. Accel-Express Inc. a. The weighted score for Location A: 108  107  104  207  204  307  620 The weighted score for Location B: 105  107  107  204  208  306  610 Location A must be chosen. b. If equal weights are placed on the criteria, the two locations will be tied because the sum of the scores is 37 for both A and B.

15. Build-Rite Construction a. Maximin Criterion—Best Decision: Subcontract ... Payoff: $100,000 b. Maximax Criterion—Best Decision: Hire ... Payoff: $625,000 c. Laplace Criterion—Best Decision: Subcontract ... Weighted Payoff: $221,667 Alternative Weighted Payoff Hire $250,000 100,000  $625,000 3  $158,333 Subcontract $100,000 150,000  $415,000 3  $221,667 Do nothing $50,000  80,000  $300,000 3  $143,333 d. Minimax Regret Criterion—Subcontract ... Minimum Maximum Regret $210,000 Regrets ($000) Demand for Home Improvements Alternative Low Moderate High Maximum Hire 100  250  350 150 100  50 625  625  0 350 Subcontract 100 100  0 150 150  0 625  415  210 210 Hire 100  50  50 150  80  70 625  300  325 325

16. Decision Tree (0.5) $15 (0.5) $30 $22.50

(0.4) 2 $20.60 $20 Alternative 1 $22.50 (0.3) $18 (0.3) $24 1

$25 Alternative 2 $24.00 (0.2) 3 (0.6) $20 (0.4) $25.00 $24 $30 (0.5) $26 (0.3) $20 Work from right to left. Here we begin with Decision Node 2, although Decision Node 3 would be an equally good starting point. The key concept is that we cannot begin analysis of Decision Node 1 until we know the expected payoffs for Decision Nodes 2 and 3. Decision Node 2 1. Its first alternative (in the upper right portion of the tree) leads to an event node with an expected payoff of $22.50 [or 0.5(15) + 0.5(30)]. 2. Its second alternative leading downward reaches an event node with an expected payoff of $20.60 [or 0.4(20) + 0.3(18)+ 0.3(24)]. 3. Thus the expected payoff for decision node 2 is $22.50, because the first alternative has the better expected payoff. Prune the second alternative. Decision Node 3 4. Its second alternative leads to an event node has an expected payoff of $24 [or 0.6(20) + 0.4(30)]. 5. Thus the payoff for decision node 3 is $25, because the first alternative ($25) is better than the expected payoff for the second alternative ($24). Prune the second alternative. Decision Node 1 6. The second alternative leads to an event node has an expected payoff of $24 [or 0.2(25) + 0.5(26)+ 0.3(20)]. 7. Thus the expected payoff for decision node 1 is $24, because the second alternative ($24) is better than the expected payoff for the second alternative ($22.50). Prune the first alternative. Thus the best initial choice (Decision 1) is to select the lower branch, Alternative 2. If the top branch of the subsequent event occurs (a 20% probability), then Decision 3 must be made. Select its first alternative. Conclusion: Select the lower branch, with an expected payoff of $24.

17. One machine or two. a. Decision Tree Subcontract $160,000 High demand (0.80) 2 Do nothing $120,000 Buy second $140,000 $152,000 $160,000

One Low demand (0.20) $120,000 1 Two $162,000 High demand (0.80) $180,000 Low demand (0.20) $90,000 b. Working from right to left: Decision Node 2 1. The best choice is to subcontact ($160,000), which becomes the expected payoff for Decision Node 2. Prune the “Do nothing” and Buy second” alternatives. Decision Node 1 2. The alternative to buy one machine has an expected value of $152,000 [or 0.8(160,000) + 0.2(120,000]. 3. The alternative to buy two machines has an expected value of $162,000 [or 0.8(180,000) + 0.2(90,000]. 4. Thus the best choice is to buy two machines because it has a higher expected payoff ($162,000 versus $152,000). Prune the one machine alternative. Conclusion: Buy two machines, with an expected payoff of $162,000.

18. Small, medium, or large facility. a. Decision Tree

High demand (0.35) $220,000 Average demand (0.40) $125,000 Low demand (0.25) ($60,000) $112,000 Large Expand lrg $145,000 High demand (0.35) Dofac nothing 2 $150,000 Medium 1 Average demand (0.40) $140,000 $102,250 Low demand (0.25) ($25,000) Expand lrg $125,000 Small Expandfac med High demand (0.35) 3 $60,000 $78,250 Doac nothing $75,000

Average demand (0.40) 4 Expand med $60,000 Do nothing $75,000 Low demand (0.25) $18,000

Copyright © 2013 Pearson Education, Inc. Publishing as Prentice Hall. Decision Making  SUPPLEMENT A A-13 b. Working from right to left: Decision Node 2 1. The best choice is to do nothing ($150,000), which becomes the expected payoff for Decision Node 2. Prune the “Expand to large” alternative. Decision Node 3 2. The best choice is the “Expand to large” alternative ($125,000), which becomes the expected payoff for Decision Node 3. Prune the “Expand to medium” and “Do nothing” alternatives. Decision Node 4 3. The best choice is to do nothing ($75,000), which becomes the expected payoff for Decision Node 4. Prune the “Expand to medium” alternative. Decision Node 1 4. The alternative to build a large facility has an expected payoff of $112,000 [or 0.35(220,000) + 0.40(125,000) + 0.25(60,000)]. 5. The alternative to build a medium-sized facility has an expected payoff of $102,250 [or 0.35(150,000) + 0.40(140,000) + 0.25(25,000]. 6. The alternative to build a small facility has an expected payoff of $78,250 [or 0.35(125,000) + 0.40(75,000) + 0.25(18,000]. 7. Thus the best choice is to build a large facility because it has a higher expected payoff ($112,000). Prune the medium and small alternatives. Conclusion: Build the large facility, with an expected payoff of $112,000. c. Develop a payoff table from tree created in part a

Decision High Demand Average Demand Low Demand Small Facility $125,000 $75,000 $18,000 Medium Facility $150,000 $140,000 ($25,000) Large Facility $220,000 $125,000 ($60,000)

Maximin Criterion—Best Decision: Small Facility Maximax Criterion—Best Decision: Large Facility Minimax Regret Criterion—Best Decision: Medium Facility

Regrets ($000) Alternative High Average Low Maximum Small 220-125=95 140-75=65 18-18=0 95 Medium 220-150=70 140-140=0 18-(25)=43 70 Large 220-220=0 140-125=15 18-(60)=78 78

19. Small or large plant. a. Decision Tree (payoffs are in millions of dollars)

Expand $14 High demand (0.70) 2 Do nothing $10 $12.2 million Small Low demand (0.30) $8

Large High demand (0.70) $18 $14.1 million Low demand (0.30) $5 b. Working from right to left: Decision Node 2 1. The best choice is the “Expand” alternative ($14), which becomes the expected payoff for Decision Node 2. Prune the “Do nothing” alternative. Decision Node 1 2. The alternative to build a small plant has an expected payoff of $12.2 million [or 0.70(14) + 0.30(8)]. 3. The alternative to build a large plant has an expected payoff of $14.1 million [or 0.70(18) + 0.30(5)]. 4. Thus the best choice is to build a large plant because it has a higher expected payoff ($14.1 million). Prune the small plant alternative. Conclusion: Build the large facility, with an expected payoff of $14.1 million.

20. Offshore Chemicals The decision tree would have just one decision node with two branches (“build” and “do not build”). The “build” alternative is followed by an event node: “Facility works” (0.40) and “Facility fails” (0.60). Decision Node 1 1. The “build” alternative has an expected payoff of $2,000,000 [or 0.4 ($20,000,000) + 0.6 (–$10,000,000)] 2. The “do not build” has a payoff of $0. 3. Thus the best choice, based on the expected value criterion, is to build. Prune the “Do not build” alternative. Conclusion: Build the facility, with an expected payoff of $2 million. Of course, political or environmental considerations might also influence the final decision.