NGC 1912 and NGC 1907: a Close Encounter Between Open Clusters?
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
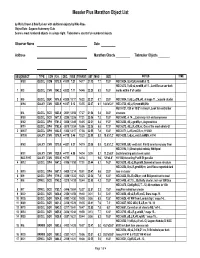
Messier Plus Marathon Text
Messier Plus Marathon Object List by Wally Brown & Bob Buckner with additional objects by Mike Roos Object Data - Saguaro Astronomy Club Score is most numbered objects in a single night. Tiebreaker is count of un-numbered objects Observer Name Date Address Marathon Obects __________ Tiebreaker Objects ________ SEQ OBJECT TYPE CON R.A. DEC. RISE TRANSIT SET MAG SIZE NOTES TIME M 53 GLOCL COM 1312.9 +1810 7:21 14:17 21:12 7.7 13.0' NGC 5024, !B,vC,iR,vvmbM,st 12.. NGC 5272, !!,eB,vL,vsmbM,st 11.., Lord Rosse-sev dark 1 M 3 GLOCL CVN 1342.2 +2822 7:11 14:46 22:20 6.3 18.0' marks within 5' of center 2 M 5 GLOCL SER 1518.5 +0205 10:17 16:22 22:27 5.7 23.0' NGC 5904, !!,vB,L,eCM,eRi, st mags 11...;superb cluster M 94 GALXY CVN 1250.9 +4107 5:12 13:55 22:37 8.1 14.4'x12.1' NGC 4736, vB,L,iR,vsvmbM,BN,r NGC 6121, Cl,8 or 10 B* in line,rrr, Look for central bar M 4 GLOCL SCO 1623.6 -2631 12:56 17:27 21:58 5.4 36.0' structure M 80 GLOCL SCO 1617.0 -2258 12:36 17:21 22:06 7.3 10.0' NGC 6093, st 14..., Extremely rich and compressed M 62 GLOCL OPH 1701.2 -3006 13:49 18:05 22:21 6.4 15.0' NGC 6266, vB,L,gmbM,rrr, Asymmetrical M 19 GLOCL OPH 1702.6 -2615 13:34 18:06 22:38 6.8 17.0' NGC 6273, vB,L,R,vCM,rrr, One of the most oblate GC 3 M 107 GLOCL OPH 1632.5 -1303 12:17 17:36 22:55 7.8 13.0' NGC 6171, L,vRi,vmC,R,rrr, H VI 40 M 106 GALXY CVN 1218.9 +4718 3:46 13:23 22:59 8.3 18.6'x7.2' NGC 4258, !,vB,vL,vmE0,sbMBN, H V 43 M 63 GALXY CVN 1315.8 +4201 5:31 14:19 23:08 8.5 12.6'x7.2' NGC 5055, BN, vsvB stell. -

Winter Constellations
Winter Constellations *Orion *Canis Major *Monoceros *Canis Minor *Gemini *Auriga *Taurus *Eradinus *Lepus *Monoceros *Cancer *Lynx *Ursa Major *Ursa Minor *Draco *Camelopardalis *Cassiopeia *Cepheus *Andromeda *Perseus *Lacerta *Pegasus *Triangulum *Aries *Pisces *Cetus *Leo (rising) *Hydra (rising) *Canes Venatici (rising) Orion--Myth: Orion, the great hunter. In one myth, Orion boasted he would kill all the wild animals on the earth. But, the earth goddess Gaia, who was the protector of all animals, produced a gigantic scorpion, whose body was so heavily encased that Orion was unable to pierce through the armour, and was himself stung to death. His companion Artemis was greatly saddened and arranged for Orion to be immortalised among the stars. Scorpius, the scorpion, was placed on the opposite side of the sky so that Orion would never be hurt by it again. To this day, Orion is never seen in the sky at the same time as Scorpius. DSO’s ● ***M42 “Orion Nebula” (Neb) with Trapezium A stellar nursery where new stars are being born, perhaps a thousand stars. These are immense clouds of interstellar gas and dust collapse inward to form stars, mainly of ionized hydrogen which gives off the red glow so dominant, and also ionized greenish oxygen gas. The youngest stars may be less than 300,000 years old, even as young as 10,000 years old (compared to the Sun, 4.6 billion years old). 1300 ly. 1 ● *M43--(Neb) “De Marin’s Nebula” The star-forming “comma-shaped” region connected to the Orion Nebula. ● *M78--(Neb) Hard to see. A star-forming region connected to the Orion Nebula. -

Central Coast Astronomy Virtual Star Party January 16Th 7Pm Pacific
Central Coast Astronomy Virtual Star Party January 16th 7pm Pacific Welcome to our Virtual Star Gazing session! We’ll be focusing on objects you can see with binoculars or a small telescope, so after our session, you can simply walk outside, look up, and understand what you’re looking at. CCAS President Aurora Lipper and astronomer Kent Wallace will bring you a virtual “tour of the night sky” where you can discover, learn, and ask questions as we go along! All you need is an internet connection. You can use an iPad, laptop, computer or cell phone. When 7pm on Saturday night rolls around, click the link on our website to join our class. CentralCoastAstronomy.org/stargaze Before our session starts: Step 1: Download your free map of the night sky: SkyMaps.com They have it available for Northern and Southern hemispheres. Step 2: Print out this document and use it to take notes during our time on Saturday. This document highlights the objects we will focus on in our session together. Celestial Objects: Moon: The moon is 3 days past new, which is really good for star gazing. Be sure to look at the moon tonight with your naked eyes and/or binoculars! Mercury is rising into the western sky and may be a good target near the end of the month. Mars is up high but is shrinking in size as the weeks progress. *Image credit: all astrophotography images are courtesy of NASA unless otherwise noted. All planetarium images are courtesy of Stellarium. Central Coast Astronomy CentralCoastAstronomy.org Page 1 Main Focus for the Session: 1. -

A Basic Requirement for Studying the Heavens Is Determining Where In
Abasic requirement for studying the heavens is determining where in the sky things are. To specify sky positions, astronomers have developed several coordinate systems. Each uses a coordinate grid projected on to the celestial sphere, in analogy to the geographic coordinate system used on the surface of the Earth. The coordinate systems differ only in their choice of the fundamental plane, which divides the sky into two equal hemispheres along a great circle (the fundamental plane of the geographic system is the Earth's equator) . Each coordinate system is named for its choice of fundamental plane. The equatorial coordinate system is probably the most widely used celestial coordinate system. It is also the one most closely related to the geographic coordinate system, because they use the same fun damental plane and the same poles. The projection of the Earth's equator onto the celestial sphere is called the celestial equator. Similarly, projecting the geographic poles on to the celest ial sphere defines the north and south celestial poles. However, there is an important difference between the equatorial and geographic coordinate systems: the geographic system is fixed to the Earth; it rotates as the Earth does . The equatorial system is fixed to the stars, so it appears to rotate across the sky with the stars, but of course it's really the Earth rotating under the fixed sky. The latitudinal (latitude-like) angle of the equatorial system is called declination (Dec for short) . It measures the angle of an object above or below the celestial equator. The longitud inal angle is called the right ascension (RA for short). -

LIST of PUBLICATIONS Aryabhatta Research Institute of Observational Sciences ARIES (An Autonomous Scientific Research Institute
LIST OF PUBLICATIONS Aryabhatta Research Institute of Observational Sciences ARIES (An Autonomous Scientific Research Institute of Department of Science and Technology, Govt. of India) Manora Peak, Naini Tal - 263 129, India (1955−2020) ABBREVIATIONS AA: Astronomy and Astrophysics AASS: Astronomy and Astrophysics Supplement Series ACTA: Acta Astronomica AJ: Astronomical Journal ANG: Annals de Geophysique Ap. J.: Astrophysical Journal ASP: Astronomical Society of Pacific ASR: Advances in Space Research ASS: Astrophysics and Space Science AE: Atmospheric Environment ASL: Atmospheric Science Letters BA: Baltic Astronomy BAC: Bulletin Astronomical Institute of Czechoslovakia BASI: Bulletin of the Astronomical Society of India BIVS: Bulletin of the Indian Vacuum Society BNIS: Bulletin of National Institute of Sciences CJAA: Chinese Journal of Astronomy and Astrophysics CS: Current Science EPS: Earth Planets Space GRL : Geophysical Research Letters IAU: International Astronomical Union IBVS: Information Bulletin on Variable Stars IJHS: Indian Journal of History of Science IJPAP: Indian Journal of Pure and Applied Physics IJRSP: Indian Journal of Radio and Space Physics INSA: Indian National Science Academy JAA: Journal of Astrophysics and Astronomy JAMC: Journal of Applied Meterology and Climatology JATP: Journal of Atmospheric and Terrestrial Physics JBAA: Journal of British Astronomical Association JCAP: Journal of Cosmology and Astroparticle Physics JESS : Jr. of Earth System Science JGR : Journal of Geophysical Research JIGR: Journal of Indian -

Patrick Moore's Practical Astronomy Series
Patrick Moore’s Practical Astronomy Series Other Titles in this Series Telescopes and Techniques (2nd Edn.) Observing the Planets Chris Kitchin Peter T. Wlasuk The Art and Science of CCD Astronomy Light Pollution David Ratledge (Ed.) Bob Mizon The Observer’s Year Using the Meade ETX Patrick Moore Mike Weasner Seeing Stars Practical Amateur Spectroscopy Chris Kitchin and Robert W. Forrest Stephen F. Tonkin (Ed.) Photo-guide to the Constellations More Small Astronomical Observatories Chris Kitchin Patrick Moore (Ed.) The Sun in Eclipse Observer’s Guide to Stellar Evolution Michael Maunder and Patrick Moore Mike Inglis Software and Data for Practical Astronomers How to Observe the Sun Safely David Ratledge Lee Macdonald Amateur Telescope Making The Practical Astronomer’s Deep-Sky Stephen F. Tonkin (Ed.) Companion Observing Meteors, Comets, Supernovae and Jess K. Gilmour other Transient Phenomena Observing Comets Neil Bone Nick James and Gerald North Astronomical Equipment for Amateurs Observing Variable Stars Martin Mobberley Gerry A. Good Transit: When Planets Cross the Sun Visual Astronomy in the Suburbs Michael Maunder and Patrick Moore Antony Cooke Practical Astrophotography Astronomy of the Milky Way: The Observer’s Jeffrey R. Charles Guide to the Northern and Southern Milky Way Observing the Moon (2 volumes) Peter T. Wlasuk Mike Inglis Deep-Sky Observing The NexStar User Guide Steven R. Coe Michael W. Swanson AstroFAQs Observing Binary and Double Stars Stephen F. Tonkin Bob Argyle (Ed.) The Deep-Sky Observer’s Year Navigating the Night Sky Grant Privett and Paul Parsons Guilherme de Almeida Field Guide to the Deep Sky Objects The New Amateur Astronomer Mike Inglis Martin Mobberley Choosing and Using a Schmidt-Cassegrain Care of Astronomical Telescopes and Telescope Accessories Rod Mollise M. -

SAC's 110 Best of the NGC
SAC's 110 Best of the NGC by Paul Dickson Version: 1.4 | March 26, 1997 Copyright °c 1996, by Paul Dickson. All rights reserved If you purchased this book from Paul Dickson directly, please ignore this form. I already have most of this information. Why Should You Register This Book? Please register your copy of this book. I have done two book, SAC's 110 Best of the NGC and the Messier Logbook. In the works for late 1997 is a four volume set for the Herschel 400. q I am a beginner and I bought this book to get start with deep-sky observing. q I am an intermediate observer. I bought this book to observe these objects again. q I am an advance observer. I bought this book to add to my collect and/or re-observe these objects again. The book I'm registering is: q SAC's 110 Best of the NGC q Messier Logbook q I would like to purchase a copy of Herschel 400 book when it becomes available. Club Name: __________________________________________ Your Name: __________________________________________ Address: ____________________________________________ City: __________________ State: ____ Zip Code: _________ Mail this to: or E-mail it to: Paul Dickson 7714 N 36th Ave [email protected] Phoenix, AZ 85051-6401 After Observing the Messier Catalog, Try this Observing List: SAC's 110 Best of the NGC [email protected] http://www.seds.org/pub/info/newsletters/sacnews/html/sac.110.best.ngc.html SAC's 110 Best of the NGC is an observing list of some of the best objects after those in the Messier Catalog. -

SAA 100 Club
S.A.A. 100 Observing Club Raleigh Astronomy Club Version 1.2 07-AUG-2005 Introduction Welcome to the S.A.A. 100 Observing Club! This list started on the USENET newsgroup sci.astro.amateur when someone asked about everyone’s favorite, non-Messier objects for medium sized telescopes (8-12”). The members of the group nominated objects and voted for their favorites. The top 100 objects, by number of votes, were collected and ranked into a list that was published. This list is a good next step for someone who has observed all the objects on the Messier list. Since it includes objects in both the Northern and Southern Hemispheres (DEC +72 to -72), the award has two different levels to accommodate those observers who aren't able to travel. The first level, the Silver SAA 100 award requires 88 objects (all visible from North Carolina). The Gold SAA 100 Award requires all 100 objects to be observed. One further note, many of these objects are on other observing lists, especially Patrick Moore's Caldwell list. For convenience, there is a table mapping various SAA100 objects with their Caldwell counterparts. This will facilitate observers who are working or have worked on these lists of objects. We hope you enjoy looking at all the great objects recommended by other avid astronomers! Rules In order to earn the Silver certificate for the program, the applicant must meet the following qualifications: 1. Be a member in good standing of the Raleigh Astronomy Club. 2. Observe 80 Silver observations. 3. Record the time and date of each observation. -

The Star Clusters Young & Old Newsletter
SCYON The Star Clusters Young & Old Newsletter edited by Holger Baumgardt, Ernst Paunzen and Pavel Kroupa SCYON can be found at URL: http://astro.u-strasbg.fr/scyon SCYON Issue No. 34 16 July 2007 EDITORIAL Here is the 34th issue of the SCYON newsletter. The current issue contains 35 abstracts from refereed journals, and an announcement for the MODEST-8 meeting in Bonn in December. The next issue will be sent out in September. We wish everybody a productive summer... Thank you to all those who sent in their contributions. Holger Baumgardt, Ernst Paunzen and Pavel Kroupa ................................................... ................................................. CONTENTS Editorial .......................................... ...............................................1 SCYON policy ........................................ ...........................................2 Mirror sites ........................................ ..............................................2 Abstract from/submitted to REFEREED JOURNALS ........... ................................3 1. Star Forming Regions ............................... ........................................3 2. Galactic Open Clusters............................. .........................................6 3. Galactic Globular Clusters ......................... ........................................16 4. Galactic Center Clusters ........................... ........................................23 5. Extragalactic Clusters............................ ..........................................24 -

Binocular Universe: Aurigan Treasures
Binocular Universe: Aurigan Treasures February 2012 Phil Harrington ead outside this evening and take a look high overhead. If you live in midnorthern latitudes, you will find a lone beacon cresting near the zenith as Hthe sky darkens. That's Capella, the Alpha (α) star of the constellation Auriga the Charioteer. Tracing back to ancient Rome, the name Capella translates as "She-Goat," a reference to the position it holds in the picture of the Charioteer. He is often portrayed as holding a goat and two kids in his arms. Above: Winter star map from Star Watch by Phil Harrington. Finder chart for this month's Binocular Universe, adapted from TUBA, www.philharrington.net/tuba.htm Today, we know that Capella is actually a binary star system lying some 42 light years away. Each of Capella's suns is classified as a type-G yellow star, like our Sun. That means that all three have roughly the same surface temperature, although our yellow dwarf Sun is only about one-tenth as large as either of the Capella giants. There is little hope of spotting the two Capella component stars through even the largest telescopes, since they are only separated by about 60 million miles, less than the distance from the Sun to Venus. The Charioteer’s pentagonal body highlights a wonderful area of the winter sky to scan with binoculars. There, you will find three of the season’s brightest open star clusters as well as an array of lesser known targets. M38, one of Auriga's three Messier open clusters, is centrally positioned within Auriga’s pentagonal body. -

Making a Sky Atlas
Appendix A Making a Sky Atlas Although a number of very advanced sky atlases are now available in print, none is likely to be ideal for any given task. Published atlases will probably have too few or too many guide stars, too few or too many deep-sky objects plotted in them, wrong- size charts, etc. I found that with MegaStar I could design and make, specifically for my survey, a “just right” personalized atlas. My atlas consists of 108 charts, each about twenty square degrees in size, with guide stars down to magnitude 8.9. I used only the northernmost 78 charts, since I observed the sky only down to –35°. On the charts I plotted only the objects I wanted to observe. In addition I made enlargements of small, overcrowded areas (“quad charts”) as well as separate large-scale charts for the Virgo Galaxy Cluster, the latter with guide stars down to magnitude 11.4. I put the charts in plastic sheet protectors in a three-ring binder, taking them out and plac- ing them on my telescope mount’s clipboard as needed. To find an object I would use the 35 mm finder (except in the Virgo Cluster, where I used the 60 mm as the finder) to point the ensemble of telescopes at the indicated spot among the guide stars. If the object was not seen in the 35 mm, as it usually was not, I would then look in the larger telescopes. If the object was not immediately visible even in the primary telescope – a not uncommon occur- rence due to inexact initial pointing – I would then scan around for it. -

Mass Functions and Photometric Binaries in Nine Open Clusters
Mass functions and photometric binaries in nine open clusters Saurabh Sharma1, A. K. Pandey1, K. Ogura2, T. Aoki3, Kavita Pandey4, T. S. Sandhu1,5 and R. Sagar1 Received ...../ Accepted ..... ABSTRACT Using homogeneous CCD photometric data from the 105-cm Kiso Schmidt telescope covering a 50′ 50′ field, we study the mass functions (MFs) of nine open clusters. The ages and Galac- tocentric× distances of the target clusters vary from 16 - 2000 Myr and 9-10.8 kpc, respectively. The values of MF slopes vary from -1.1 to -2.1. The classical value derived by Salpeter (1955) for the slope of the IMF is Γ = 1.35. The MFs in the outer regions of the clusters are found to be steeper than in the inner regions,− indicating the presence of mass segregation in the clusters. The MF slopes (in the outer region as well as the whole cluster) undergo an exponential decay with the evolutionary parameter τ (= age/ relaxation time). It seems that the evaporation of low-mass members from outer regions of the clusters is not significant at larger Galactocentric distances. It is concluded that the initial mass function (IMF) in the anticentre direction of the Galaxy might have been steeper than the IMF in the opposite direction. A comparison of the observed CMDs of the clusters with synthetic CMDs gives a photometric binary content of 40%. ∼ Subject headings: Galaxy: open clusters and associations- Technique: photometric- Stars: luminosity function, mass function- 1. Introduction considerations suggest that the IMF ought to de- pend on star-forming conditions (Larson 1998). The distribution of stellar masses that form in Therefore it is important to find systematic varia- a star-formation event in a given volume of space tions of the IMF with different star-forming condi- is called the Initial Mass Function (IMF) and to- tions.