Supplementary Material 1

1Supplementary Material 1 2

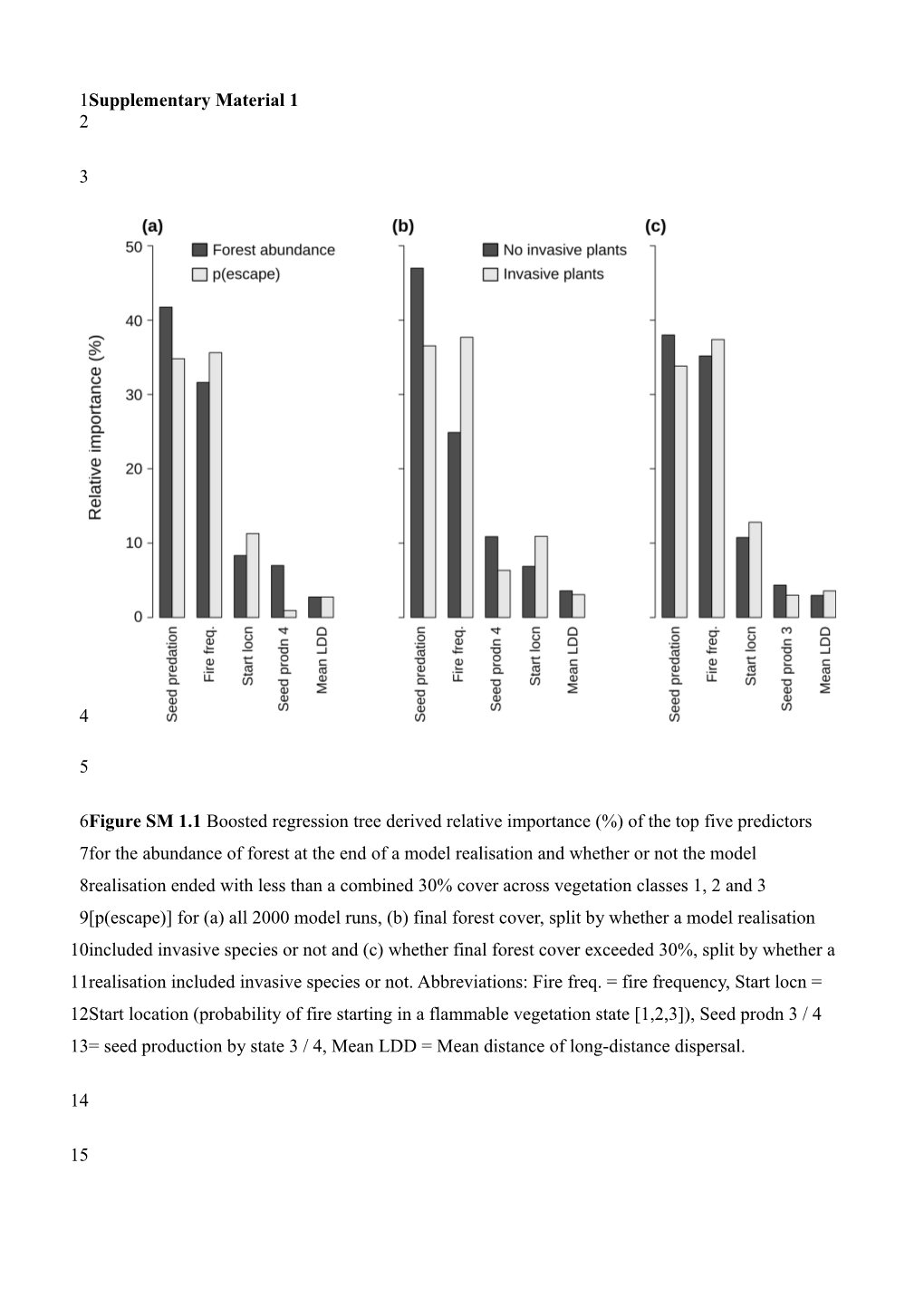
6Figure SM 1.1 Boosted regression tree derived relative importance (%) of the top five predictors 7for the abundance of forest at the end of a model realisation and whether or not the model 8realisation ended with less than a combined 30% cover across vegetation classes 1, 2 and 3 9[p(escape)] for (a) all 2000 model runs, (b) final forest cover, split by whether a model realisation 10included invasive species or not and (c) whether final forest cover exceeded 30%, split by whether a 11realisation included invasive species or not. Abbreviations: Fire freq. = fire frequency, Start locn = 12Start location (probability of fire starting in a flammable vegetation state [1,2,3]), Seed prodn 3 / 4 13= seed production by state 3 / 4, Mean LDD = Mean distance of long-distance dispersal.

2Figure SM 1.2 Positive feedbacks between vegetation and fire are evident at multiple scales; in the 3composition of: (a) the ignition cell, (b) the immediate neighbourhood (nhb) of the ignition cell 4(number of the eight cells neighbouring the ignition location in states 1 or 2), and (c) the entire 5landscape (flammability scaled from 0 to 1, with 1 representing the case where the landscape 6comprises only the most flammable vegetation). These interactions differ in strength when invasive 7plants are present, and affect (d) the fire size-frequency distribution (represented here by the 8probability density distribution of fire sizes [proportion of landscape burned]; the dashed black line 9represents the distribution for all fires [(that is, whether with or without invasive plants]). In all 10sub-plots red shading denotes model realisations where invasive plants were present and blue 11denotes model realisations where invasive plants were absent. 1

5 6Figure SM 1.3 Effect of changes in dispersal limitation on time required for the landscape to (a) 7achieve 95% forest cover, and (b) escape the flammable state (less than 30% in classes 1, 2, or 3). 8In all cases fire frequency is set to zero. Points are median values and the shaded areas 95% 9percentiles; red and blue represent baseline and 50% reduced propagule reduction. 10 1 2 3Figure SM 1.4 Median Gini values (a measure of compositional evenness) as a function of fire 4frequency with (red) and without (blue) invasive pyrophyllic plant species. The dashed lines show 5the 95% percentile limits. Note the restricted range of fire frequencies under which a range of 6landscape compositions emerge. 7 8 1 1Table SM 1.1 Model Parameterization, Baseline Values, Range Used in Uncertainty Analysis (all uniform deviates) and Source of 2Information and Interpretation Parameter Description Baseline Uncertainty Source value analysis range

Landscape

Initial abundance Abundance of five vegetation classes in the landscape (based on satellite {0.05, 0.30, LCDB 3.0 database (Land data collected over the Austral summer of 2008/9). 0.25, 0.20, Information NZ); resolution = one 0.20}** ha; overall accuracy > 95% See: http://www.lcdb.scinfo.org.nz/

Vegetation dynamics

Successional rates Minimum time spent in each of the vegetation classes before transition See Figure 1 Field observation, published values expert opinion (see also Perry and others 2010)

Propagule production Number of 'propagules' produced per cell per year by class 3 vegetation 4 per cell per 2 - 8 Approximated from demographic class 3 yr data in Enright and Watson (1992) and West (1995). See SM 2 for full details.

Propagule production Number of 'propagules' produced per cell per year by class 4 vegetation 4 per cell per 2 - 8 Approximated from demographic class 4 yr data in Enright and Watson (1992) and West (1995). See SM 2 for full details.

Mean fruit movement Mean distance propagules moved from parent cell by birds (mean of 4 cells (80 1 - 8 After Wotton and Kelly (2012) who distance (LDD) Exponential deviate) m) report mean dispersal distances of 95, 98 and 61 m for three fleshy- fruited tree species in NZ.

Critical density for Minimum density of 'saplings' required for transition from class 2 to 3 10 per cell 5 - 20 Estimated from field-data transition class 2 → 3 (250/ha) describing stand structure in the four vegetation states. See SM 2 for full details.

2 5 1 Parameter Description Baseline Uncertainty Source value analysis range

Critical density for Minimum density of 'saplings' required for transition from class 3 to 4 10 per cell 5 - 20 Estimated from field-data . transition class 3 → 4 (250/ha) describing stand structure in the four vegetation states. See SM 2 for full details.

Post-fire invasion

Base invasion post- Base probability of invasive species invading a grid cell post-fire 0.05 0.005 - 0.15 No empirical data. fire

Invasion risk increase Increase in invasion risk per number of fires in last three decades that a 0.10 0.05 - 0.20 No empirical data. cell has experienced.

Slow rate Rate at which transition out of post-fire class (states 0 and 1) is slowed 2 yr 1 - 5 No empirical data. per number of fires in last three decades that a cell has experienced.

Fire regime

Fire frequency Probability of a fire event in any given year 0.10 0.0 – 0.25

Fire start Probability that a fire will start in a flammable cell (class 0 or class 1) or 0.50 0.0 – 1.0 No empirical data but the vast a randomly located cell of any vegetation type. majority of fires in NZ are anthropogenic (Anderson and others 2008) and are most likely to start in flammable areas of the landscape.

1 ** Initial vegetation composition was estimated from the LCD 3.0 database. Three LCDB classes account for nearly 90% of 2landcover on GBI (the others relate to urban or agricultural land): ‘indigenous forest’, ‘indigenous hardwood forest’, and ‘mānuka 3and/or kānuka’. The mānuka shrubland (state 2) and kānuka tall shrubland (state 3) states were allocated at a 60:40 ratio across 4the LCDB mānuka/kānuka class (so 35% and 25%) and the young (state 4) and mature (state 5) forest modelled states were 5allocated at a 50:50 ratio to the two LCDB indigenous forest classes (so 20% and 20%). In model scenarios where the model 6represented invaded shrubland 5% of the mānuka shrubland was allocated to that state (1) (giving cover in states 1, 2 and 3 of 5%, 730% and 25%, respectively).

1Supplementary Material 2 - Dispersal and propagule production 2 3It is computationally expensive to simulate all seeds produced in a landscape and follow the fate of 4all individuals produced, especially given the high-levels of mortality in small size-classes for 5forest trees. To approximately estimate survival in the smaller size classes of typical mid- to late- 6successional forest tree species we use the fecundity and demographic information provided in 7Enright (1992), Enright and Watson (1992) for Rhopalostylis sapida (nikau) in secondary Agathis 8australis forest near Auckland and West (1995) for Beilschmiedia tawa (tawa) in tawa-dominated 9'virgin' forest at Pureora Forest Park. There is a lack of detailed demographic data available for 10long-lived NZ tree species but B. tawa and R. sapida are representative of species occurring in 11mature podocarp-hardwood forest in northern NZ. We consider the dynamics of two classes 12(‘seedlings’ and ‘saplings’) of individuals and so in, effect, within each grid-cell there is a 13transition (Lefkovitch) matrix (Figure SM 2.1). Seedlings are individuals in the size range 30 cm 14– 1.5 m height (c 10 years old for tawa) and saplings have height greater than 1.5 m (c. 40 years 15old for tawa). Individuals accumulate in the sapling class, which is therefore effectively size 16unbounded but does suffer background mortality. 17 18To estimate seedling production: 191. We estimate total viable seed production per grid cell after accounting for seed predation (seed 20production data from Enright (1992) and West (1995) 212. From the stage-specific mortality rates presented in the life-tables in Enright and Watson (1992) 22and West (1995), we used the methods described in Barot and others (2002) to estimate the typical 23age of an individual of seedling size (via the ‘age of residence’ so not assuming a SSD) and hence 24the probability of a viable seed surviving to seedling size. 253. Multiplying step 1. by step 2. yields an approximate annual production of seedling-sized 26individuals per unit area (in our case 20 × 20 m grid cell). 27 28So, for example, using information in West (1995) from her ‘virgin’ site (her Tables 3 and 4) we 29have: 30 1.2 × 104 seeds per ha per yr × 0.0265 [germination rate] × 0.1013 [survival post- 31 germination to stage class] = 31.8 15 cm seedlings per ha per year [ 2 seedlings per 0.04 32 ha grid cell]

1 2We then use the demographic rates provided in Enright and Watson (1992) and West (1995) to 3parameterise Lefkovitch models incorporating seedling mortality, transition of seedlings to 4saplings and sapling mortality. The values derived from the life-tables and transition matrices are 5quite similar for both species and also suggest high levels of spatial and temporal variability in 6life-history rates. Thus we used the same rates for the stage 3 and stage 4 juveniles of seedling 7survival = 0.9, seedling to sapling transition = 0.05 and sapling survival = 0.99. Input of seedlings 8is spatially variable. 9 10To estimate critical transition densities: 11Using the point centred quarter (PCQ) data described in Perry and others 2010 we identified stem 12densities (stems > 5 cm DBH / ha) in stages 3 and 4 for the ‘species’ of interest, these equated to 13340 and 500 stems per ha (noting that these are based on stands that had transitioned to the stage at 14some point in the past, whereas we are interested in the point of transition). For both stages we set 15a baseline minimal density of 250 stems per ha (10 stems per modelled grid cell) in the larger of 16the two matrix size classes for transition to occur. 17 18The representation of the regeneration dynamic described here is simple and the parameterisation 19values used are approximate and do not include natural variability (for example, inter-annual seed 20production). However, they capture the dynamics of the system and uncertainty analyses (Fig SM 211) suggest that uncertainty in these parameter values is overwhelmed by the dominant variables of 22fire frequency and seed predation. 23 24 25 26 27 28 29

1 2 3Figure SM2-1 Schematic overview of transition matrix based representation of within grid cell 4regeneration dynamics in the model. 5 6 7References 8Barot S, Gignoux J, Legendre S. 2002. Stage-classified matrix models and age estimates. Oikos

9 96:56–61.

10Enright NJ. 1992. Factors affecting reproductive behaviour in the New Zealand nikau palm,

11 Rhopalostylis sapida Wendl. et Drude. New Zealand Journal of Botany 30:69–80.

12Enright NJ, Watson AD. 1992. Population dynamics of the nikau palm Rhopalostylis sapida in

13 a temperate rainforest remnant near Auckland, New Zealand. New Zealand Journal of

14 Botany 30:29–43.

15West CJ. 1995. Sustainability of Beilschmiedia tawa-dominated forest in New-Zealand -

16 population predictions based on transition matrix model analysis. Australian Journal

17 of Botany 43:51–71.