DOCSLIB.ORG

LD5655.V856 1989.B446.Pdf

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
LD5655.V856 1989.B446.Pdf 5 .>° 9 9 Analysis, Monitoring and Control of Voltage Stability ln Electric Power Systems by Miroslav M. Begovic Dissertation submitted to the Faculty ot' the Virginia Polytechnic institute and State University ot' in partial fultillment of the requirements for the degree PhD in Electrical Engineering in The Bradley Department of Electrical Engineering APPROVED: Arun G. Phadke, Chairman ti Jaime De La Rec Lopez Saifur Rahman / V fx Kwa Sur Tam John W. Laym July, 1989 Blacksburg, Virginia Analysis, Monitoring and Control of Voltage Stability ln Electric Power Systems by Miroslav M. Begovic Arun G. Phadke, Chairman The Bradley Department of Electrical Engineering (ABSTRACT) The work presented in this text concentrates on three aspects of voltage stability studies: analysis and determination of suitable proximity indicators, design of an effective real-time monitoring system and determination of appropriate emer- gency control techniques. A simulation model of voltage collapse was built as analytical tool on'39-bus, lO·generator power system model . Voltage collapse was modeled as a saddle node bifurcation of the system dynamic model reached by increasing the system loading. Suitable indicators for real-time monitoring were found to be the minimum singular value of power flow Jacobian matrix and generated reactive powers. A study of possibilities for reducing the number of measurements of voltage phasors needed for voltage stability monitoring was also made. The idea of load bus coherency with respect to voltage dynamics was in- troduced. An algorithm was presented which determines the coherent clusters of load buses in a power system based on an arbitrary criterion function, and the analysis completed with two proposed coherency criteria. Very good agreement was obtained by simulation between the results based on accurate and approxi- mate measurements of the state vector. An algorithm was presented for identifi- l cation of critical sets of loads in a voltage unstable power system, defined as a subset of loads whose changes have the most pronounced effect on the changes of minimum singular value of load fiow Jacobian or generated reactive powers. Effects of load shedding of critical loads were investigated by simulation and fa- vorable results obtained. An investigation was also done by sensitivity analysis of proximity indicators of the effects that locations and amounts of static var compensation have on the stability margin of the system. Static compensation was found to be of limited help when voltage instabilities due to heavy system loading occur in power systems. The feasibility of implementation of the analyses and algorithms presented in this text relies on development of a feasible inte- grated monitoring and control hardware. The phasor measurcment system which was designed at Virginia Polytechnic institute and State University represents an excellent candidate for implementation of real·time monitoring and control pro- cedures. Dedication Dcdication iv Acknowledgements Writing this section for a dissertation is one of the more pleasant duties. As with any large study of this nature, it was necessary for me to obtain the help and support of many persons. lt is difficult to meaningfully thank all the people who have made this long sought dream a reality. I could not possibly do justicc to all who have hclped in large and small ways; whether they know it or not they have my gratitude. v Acknowlcdgements vi Acknowlcdgcments Table of Contents Chapter I. Introduction .................................................... 1 Chapter 2. A Survey of Research On Voltage Instability ............................ 8 2.1 Introduction ......................................................... 8 2.2 Voltage Collapse: Observations ........................................... 9 2.3 Power System Modeling and Voltage Instability .............................. 16 2.3.1 Modeling of loads ................................................. 18 2.3.2 Generator modeling ................................................ 21 2.3.3 Modeling of ULTC transformers ...................................... 26 2.3 Voltage stability studies ................................................ 29 2.4 Conclusion ......................................................... 34 Chapter 3. Voltage Stability Analysis: Simulation Approach ........................ 37 3.1 Introduction ........................................................ 37 3.2 Model definition ..................................................... 39 3.3 Simulation algorithm .................................................. 43 3.4 Power system at static bifurcation ......................................... 56 vii Table of Contents 3.5 Steady state analysis .................................................. 70 3.6 Dynamic simulation analysis ............................................ 78 3.7 Conclusions ....................................................... 115 Chapter 4. Voltage Stability Monitoring: Phasor Measurements .................... 117 4.1 lntroduction ....................................................... 117 4.2 Clustering of load buscs in power systems .................................. 124 4.2.1 Coherency Criterion 1: Sensitivity Analysis .............................. 132 4.2.2 Cohercncy Criterion 2: Dynamic Analysis ............................... 135 4.2.3 Guidelines for Application .......................................... 138 4.3 Simulation Results .................................................. 142 4.4 Conclusions ....................................................... 163 Chapter 5. Voltage Stability Emergency Control ................................ 166 5.1 Introduction ....................................................... 166 5.2 Sensitivity Analysis of Proximity lndicators ................................. 170 5.2.1 Sensitivity analysis of minimum singular values of Jacobian .................. 171 5.2.2 Sensitivity analysis of generated rcactivc powers ........................... 181 5.2.3 Selective load shcdding ............................................ 187 5.3 Simulations and Comments ............................................ 190 5.4 Conclusions ....................................................... 195 Chapter 6. Voltage Stability and Static Compensation ............................ 215 6.1 Introduction ....................................................... 215 6.2 Sensitivity Analysis of Proximity lndicators ................................. 219 6.2.1 Sensitivity analysis of minimum singular value of Jacobian .................. 227 6.2.2 Sensitivity analysis of generated reactive powers ........................... 229 Table of Contents viii 6.3 Simulations and Comments ............................................ 232 6.4 Conclusions ....................................................... 237 Chapter 7. Conclusions .................................................. 253 Bibliography .......................................................... 260 Appendix A. Parameters of Power System Model ............................... 276 Vita ................................................................ 282 Table of Contents ix List of Illustrations Figure 1. Voltage profile in major 500 kV substations of TEPCO system before the collapse. .................................. 14 Figure 2. Phasor diagram of the generator model .................. 42 Figure 3. Simulation algorithm ............................... 55 +.5x’ Figure 4. Phase portrait of: x" + sin x - sin .412 = 0 . ........ 62 Figure 5. Phase portrait of: x" +.5x’ + sin x - sin 1.56 = 0 . ........ 63 Figure 6. Voltage collapse of a two generator system. ............... 66 Figure 7. Phase angle changes before voltage collapse. .............. 67 Figure 8. Power system model used for simulations. ................ 71 Figure 9. Critical load factor estimation ........................ 74 Figure 10. Phasor diagram of the system in normal operating regime. .. 79 Figure ll. Phasor diagram of the system close to steady state instability. 80 Figure 12. Phasor diagram of the system near voltage stability boundary. 81 Figure 13. Phase angle gradients near stability boundary. ............ 82 Figure 14. Voltage gradients near stability boundary. ............... 83 Figure 15. Voltage profile and gradients in normal and voltage unstable case. 84 Figure 16. Load factor patterns for step change simulations. .......... 96 Figure 17. Voltage profile corresponding to Figure 16 (1). ............ 97 l List or Illustrations x Figure 18. Voltage profile corresponding to Figure 16 (2). ............ 98 Figure 19. Voltage profile corresponding to Figure 16 (3). ............ 99 Figure 20. Minimum eigenvalues of Jacobian for Figures 17,18,19. .... 100 Figure 21. Voltage response for various step changes of load factor. .... 101 Figure 22. System loading pattern for ramp loading. ............... 102 Figure 23. Directions of approach to stability boundary. ............ 103 Figure 24. Voltage profiles at stability boundary (scenarios i, ii, iii). .... 104 Figure 25. Voltage collapse at 10 most critical buses (scenario i). ...... 105 Figure 26. Phase angle trajectories corresponding to collapse in Figure 25. 106 Figure 27. Minimum singular values of Jacobian for collapse in Figure 25. 107 Figure 28. Reactive power generation corresponding to collapse in Figure 25. ............................................. 108 Figure 29. Reactive power generation when generation limits are observed. 109 Figure 30. Voltage collapse due to step change of k applied
Load more

Recommended publications
  • Marvel Universe by Hasbro
    Brian's Toys MARVEL Buy List Hasbro/ToyBiz Name Quantity Item Buy List Line Manufacturer Year Released Wave UPC you have TOTAL Notes Number Price to sell Last Updated: April 13, 2015 Questions/Concerns/Other Full Name: Address: Delivery Address: W730 State Road 35 Phone: Fountain City, WI 54629 Tel: 608.687.7572 ext: 3 E-mail: Referred By (please fill in) Fax: 608.687.7573 Email: [email protected] Guidelines for Brian’s Toys will require a list of your items if you are interested in receiving a price quote on your collection. It is very important that we Note: Buylist prices on this sheet may change after 30 days have an accurate description of your items so that we can give you an accurate price quote. By following the below format, you will help Selling Your Collection ensure an accurate quote for your collection. As an alternative to this excel form, we have a webapp available for http://buylist.brianstoys.com/lines/Marvel/toys . STEP 1 Please note: Yellow fields are user editable. You are capable of adding contact information above and quantities/notes below. Before we can confirm your quote, we will need to know what items you have to sell. The below list is by Marvel category. Search for each of your items and enter the quantity you want to sell in column I (see red arrow). (A hint for quick searching, press Ctrl + F to bring up excel's search box) The green total column will adjust the total as you enter in your quantities.
    [Show full text]
  • Hasbro Closes Acquisition of Saban Properties' Power Rangers And
    Hasbro Closes Acquisition of Saban Properties’ Power Rangers and other Entertainment Assets June 12, 2018 PAWTUCKET, R.I.--(BUSINESS WIRE)--Jun. 12, 2018-- Hasbro, Inc. (NASDAQ: HAS) today announced it has closed the previously announced acquisition of Saban Properties’ Power Rangers and other Entertainment Assets. The transaction was funded through a combination of cash and stock valued at $522 million. “Power Rangers will benefit from execution across Hasbro’s Brand Blueprint and distribution through our omni-channel retail relationships globally,” said Brian Goldner, Hasbro’s chairman and chief executive officer. “Informed by engaging, multi-screen entertainment, a robust and innovative product line and consumer products opportunities all built on the brand’s strong heritage of teamwork and inclusivity, we see a tremendous future for Power Rangers as part of Hasbro’s brand portfolio.” Hasbro previously paid Saban Brands$22.25 million pursuant to the Power Rangers master toy license agreement, announced by the parties in February of 2018, that was scheduled to begin in 2019. Those amounts were credited against the purchase price. Upon closing, Hasbro paid $131.23 million in cash (including a $1.48 million working capital purchase price adjustment) and $25 million was placed into an escrow account. An additional $75 million will be paid on January 3, 2019. These payments are being funded by cash on the Company’s balance sheet. In addition, the Company issued 3,074,190 shares of Hasbro common stock to Saban Properties, valued at $270 million. The transaction, including intangible amortization expense, is not expected to have a material impact on Hasbro’s 2018 results of operations.
    [Show full text]
  • Masters of the Universe: Action Figures, Customization and Masculinity
    MASTERS OF THE UNIVERSE: ACTION FIGURES, CUSTOMIZATION AND MASCULINITY Eric Sobel A Thesis Submitted to the Graduate College of Bowling Green State University in partial fulfillment of the requirements for the degree of MASTER OF ARTS December 2018 Committee: Montana Miller, Advisor Esther Clinton Jeremy Wallach ii ABSTRACT Montana Miller, Advisor This thesis places action figures, as masculinely gendered playthings and rich intertexts, into a larger context that accounts for increased nostalgia and hyperacceleration. Employing an ethnographic approach, I turn my attention to the under-discussed adults who comprise the fandom. I examine ways that individuals interact with action figures creatively, divorced from children’s play, to produce subjective experiences, negotiate the inherently consumeristic nature of their fandom, and process the gender codes and social stigma associated with classic toylines. Toy customizers, for example, act as folk artists who value authenticity, but for many, mimicking mass-produced objects is a sign of one’s skill, as seen by those working in a style inspired by Masters of the Universe figures. However, while creativity is found in delicately manipulating familiar forms, the inherent toxic masculinity of the original action figures is explored to a degree that far exceeds that of the mass-produced toys of the 1980s. Collectors similarly complicate the use of action figures, as playfully created displays act as frames where fetishization is permissible. I argue that the fetishization of action figures is a stabilizing response to ever-changing trends, yet simultaneously operates within the complex web of intertexts of which action figures are invariably tied. To highlight the action figure’s evolving role in corporate hands, I examine retro-style Reaction figures as metacultural objects that evoke Star Wars figures of the late 1970s but, unlike Star Wars toys, discourage creativity, communicating through the familiar signs of pop culture to push the figure into a mental realm where official stories are narrowly interpreted.
    [Show full text]
  • Hasbro's Iconic MR. POTATO HEAD Character Celebrates 60Th Birthday
    February 14, 2012 Hasbro's Iconic MR. POTATO HEAD Character Celebrates 60th Birthday Everyone's Favorite Tater Commemorates 60 Spud-tastic Years as a Pop Culture Icon PAWTUCKET, R.I.--(BUSINESS WIRE)-- This year, Hasbro, Inc. (NASDAQ: HAS) will mark the 60th anniversary of the Company's official "spokes spud," the MR. POTATO HEAD character. A classic rite of passage for most preschoolers, the MR. POTATO HEAD toy is one of Hasbro's most cherished characters with more than 100 million toys sold in more than 30 markets around the world. Through the past 60 years, the timeless tater has evolved from a toy box classic into a pop culture icon and has kept himself relevant by tapping into trends and entertainment. "For the past 60 years, the MR. POTATO HEAD toy has inspired imaginative play in young children and charmed fans of all ages through his roles in movies and on television." said Jerry Perez, Senior Vice President and Global Brand Leader, Playskool. "We're thrilled to see that he has evolved from classic parts and pieces to a household name that is ‘rooted' in pop culture and entertainment." The MR. POTATO HEAD character will celebrate this milestone year on his Facebook page enjoying a year of adventures with the MRS. POTATO HEAD character, starting with a birthday bash at American International Toy Fair in New York City. New product introductions for 2012 include the MASHLY IN TH LOVE MR. AND MRS. 60 ANNIVERSARY EDITION set featuring the couple holding Mr. and Mrs. Potato Head admire a birthday cake as a group sings to celebrate Mr.
    [Show full text]
  • Sp Ausnet Annual Report
    SP AUSNET ANNUAL REPORT 2007 SP AusNet employs aerial techniques using demineralised water to wash dust and soot from insulators on the transmission network in south-west Victoria. Cover Image: Ben Marsh, Apprentice Power Technician, perfecting his safe climbing skills on a transmission training tower at South Morang training centre. CONTENTS CHAIRMAN’S REPORT 8 MANAGING DIRECTOR’S REPORT 9 BOARD OF DIRECTORS 10 EXECUTIVE MANAGEMENT TEAM 12 ENERGY NETWORKS 14 BUSINESS GROWTH 22 CORPORATE SUSTAINABILITY 26 CORPORATE GOVERNANCE 30 FINANCIAL REPORTS 36 SP AUSTRALIA NETWORKS (DISTRIBUTION) LTD 37 SP AUSTRALIA NETWORKS (TRANSMISSION) LTD 99 SP AUSTRALIA NETWORKS (FINANCE) TRUST 151 SECURITYHOLDER INFORMATION 176 FINANCIAL CALENDAR 179 ANNUAL GENERAL MEETING 179 ENQUIRIES AND INFORMATION 179 GLOSSARY 180 2 SP AUSNET IS A DIVERSIFIED ENERGY INFRASTRUCTURE BUSINESS OWNING AND OPERATING VICTORIA’S PRIMARY ELECTRICITY TRANSMISSION NETWORK, AS WELL AS AN ELECTRICITY DISTRIBUTION NETWORK IN EASTERN VICTORIA AND A GAS DISTRIBUTION NETWORK IN WESTERN VICTORIA. SP AUSNET COMPRISES REGULATED ENERGY NETWORK COMPANIES – SP AUSNET TRANSMISSION AND SP AUSNET DISTRIBUTION – AND THE SP AUSNET FINANCE TRUST WHICH FINANCES THOSE COMPANIES. INVESTMENT IN SP AUSNET COMPRISES A STAPLED SECURITY CONSISTING OF ONE SHARE IN EACH OF SP AUSNET TRANSMISSION AND SP AUSNET DISTRIBUTION, AND ONE UNIT IN SP AUSNET FINANCE TRUST. SP AUSNET PRIDES ITSELF ON MAINTAINING HIGH QUALITY ENERGY NETWORKS AND IS WELL POSITIONED TO TAKE ADVANTAGE OF GROWTH WITHIN ITS REGIONS AND PARTICIPATE IN FUTURE ACQUISITION OPPORTUNITIES. Karolina Bialek, Building Services Coordinator and Kevin Murphy, Manager Financial Planning and Analysis SP AUSNET ANNUAL REPORT 2007 3 4 OUR VALUES COMMITMENT WE COMMIT TO CREATING VALUE FOR OUR CUSTOMERS, OUR PEOPLE AND OUR SECURITYHOLDERS.
    [Show full text]
  • Activision Publishing to Showcase Blockbuster Slate of Fan-Favorite Video Games at San Diego Comic-Con 2012
    Activision Publishing To Showcase Blockbuster Slate Of Fan-Favorite Video Games At San Diego Comic-Con 2012 Showgoers Will Get Their First Multiplayer Hands-On Opportunity with the Highly Anticipated TRANSFORMERS™: FALL OF CYBERTRON, Celebrate Spidey's Latest Movie Launch with Hands-On Time with The Amazing Spider-Man™, Plus a Surprise Game Reveal During the Marvel Games Panel, Exclusive Game Demos at the Activision Booth, and Much, MUCH More... SANTA MONICA, Calif., July 11, 2012 /PRNewswire/ -- Gaming, comics, sci-fi, cos-play, and fans from all walks of life the world over will experience a colossal interactive entertainment lineup from Activision Publishing, Inc., a wholly owned subsidiary of Activision Blizzard, Inc. (Nasdaq: ATVI), at San Diego Comic-Con International 2012. Headquartered at booth #5344 in the San Diego Convention Center, Activision is celebrating the theatrical release of the blockbuster hit The Amazing Spider-Man, allowing fans to go beyond the movie and find out what happens next in The Amazing Spider-Man™ video game, plus showcasing some of the most anticipated fan-favorite games in the industry, including TRANSFORMERS™: FALL OF CYBERTRON, 007™ Legends, the all-new The Walking Dead™ video game based on the hit AMC television series, along with a world premiere reveal of a brand new Super Hero video game during the Marvel Games panel on Saturday, July 14th. "We know how passionate our fans are, and San Diego Comic-Con is always a great opportunity for us to showcase our latest video games," said David Oxford, Executive Vice President, Activision Publishing. "These are big, iconic franchises and this is our chance to give back and let the hardest-of-the-hardcore play and experience our video games in a unique and fun setting before they hit stores." Activision's Full San Diego Comic-Con 2012 Booth Activities Include: ● First time multiplayer hands-on with TRANSFORMERS: FALL OF CYBERTRON video game.
    [Show full text]
  • Arxiv:2105.09511V3 [Eess.IV] 2 Jun 2021 Released At
    Medical Image Segmentation Using Squeeze-and-Expansion Transformers Shaohua Li1∗ , Xiuchao Sui1 , Xiangde Luo2 , Xinxing Xu1 , Yong Liu1 , Rick Goh1 1Institute of High Performance Computing, A*STAR, Singapore 2University of Electronic Science and Technology of China, Chengdu, China {shaohua, xiuchao.sui}@gmail.com, [email protected], {xuxinx, liuyong, gohsm}@ihpc.a-star.edu.sg Abstract the same time, i.e., learn image features that incorporate large context while keep high spatial resolutions to output fine- Medical image segmentation is important for grained segmentation masks. However, these two demands computer-aided diagnosis. Good segmentation de- pose a dilemma for CNNs, as CNNs often incorporate larger mands the model to see the big picture and fine context at the cost of reduced feature resolution. A good mea- details simultaneously, i.e., to learn image features sure of how large a model “sees” is the effective receptive field that incorporate large context while keep high spa- (effective RF) [Luo et al., 2016], i.e., the input areas which tial resolutions. To approach this goal, the most have non-negligible impacts to the model output. widely used methods – U-Net and variants, ex- Since the advent of U-Net [Ronneberger et al., 2015], it tract and fuse multi-scale features. However, the has shown excellent performance across medical image seg- fused features still have small effective receptive mentation tasks. A U-Net consists of an encoder and a de- fields with a focus on local image cues, limiting coder, in which the encoder progressively downsamples the their performance. In this work, we propose Seg- features and generates coarse contextual features that focus tran, an alternative segmentation framework based on contextual patterns, and the decoder progressively upsam- on transformers, which have unlimited effective re- ples the contextual features and fuses them with fine-grained ceptive fields even at high feature resolutions.
    [Show full text]
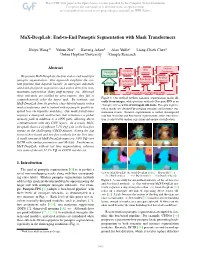
  • Max-Deeplab: End-To-End Panoptic Segmentation with Mask Transformers
    MaX-DeepLab: End-to-End Panoptic Segmentation with Mask Transformers Huiyu Wang1∗ Yukun Zhu2 Hartwig Adam2 Alan Yuille1 Liang-Chieh Chen2 1Johns Hopkins University 2Google Research Abstract Box Anchor Instance Classification Panoptic Detection Segmentation Segmentation We present MaX-DeepLab, the first end-to-end model for Anchor panoptic segmentation. Our approach simplifies the cur- Box-based Regression Semantic Segmentation rent pipeline that depends heavily on surrogate sub-tasks Ours Segmentation and hand-designed components, such as box detection, non- maximum suppression, thing-stuff merging, etc. Although Previous Methods (Panoptic-FPN) these sub-tasks are tackled by area experts, they fail to Figure 1. Our method predicts panoptic segmentation masks di- comprehensively solve the target task. By contrast, our rectly from images, while previous methods (Panoptic-FPN as an MaX-DeepLab directly predicts class-labeled masks with a example) rely on a tree of surrogate sub-tasks. Panoptic segmen- mask transformer, and is trained with a panoptic quality in- tation masks are obtained by merging semantic and instance seg- spired loss via bipartite matching. Our mask transformer mentation results. Instance segmentation is further decomposed employs a dual-path architecture that introduces a global into box detection and box-based segmentation, while box detec- memory path in addition to a CNN path, allowing direct tion is achieved by anchor regression and anchor classification. communication with any CNN layers. As a result, MaX- DeepLab shows a significant 7.1% PQ gain in the box-free regime on the challenging COCO dataset, closing the gap between box-based and box-free methods for the first time.
    [Show full text]
  • Zoning Bylaw November 2018
    Town Of Sandwich THE OLDEST TOWN ON CAPE COD Dexter Grist Mill PROTECTIVE ZONING BY-LAW November 2018 Sandwich Protective Zoning By-laws Table of Contents ARTICLE I. ADMINISTRATION AND PROCEDURE 1100. PURPOSE 1200. ADMINISTRATION 1210. Other 1220. Building Permits 1230. Certificate of Use and Occupancy 1240. Enforcement 1250. Violations 1251. Penalties 1260. Performance Bond or Deposit 1300. BOARD OF APPEALS 1310. Membership 1320. Powers of the Board of Appeals 1321. Variance 1321.1 Submission Requirements 1321.2 Referral 1322. Special Permit Granting Authority 1322. Special Permit Granting Authority 1330. Special permits 1331. Public Hearing 1332. Referral 1340. Application Requirements 1341. Review by Planning Board and Town Engineer 1342. Consideration of Recommendations 1350. Repetitive Petitions 1360. Plan Submission Requirements 1370. Appeals Under the Subdivision Control Law 1380. Special Permit for the Protection of Drinking Water Resources 1381. Criteria 1382. Submission Requirements 1390. Design and Operations Guidelines 1400. AMENDMENT 1500. VALIDITY 1600. APPLICABILITY 1700. EFFECTIVE DATE ARTICLE II. USE AND INTENSITY REGULATIONS 2100. ESTABLISHMENT OF DISTRICTS 2120. District boundary Line 2130. Lots Divided by District Boundary Line 2140. Districts 2200. USE REGULATIONS 2210. Applicability 2220. Classification of Activity 2300. USE REGULATIONS SCHEDULE 2310 Principal Uses 2320. Accessory Uses 2321. Scientific Research, Development or Related Production. 2400. NON-CONFORMING USES 2410. Abandonment. 2420. Change, Extension or Alteration 2430. Restoration 2500. INTENSITY OF USE REGULATIONS 2510. Conformance with Section 2600 2520. Change in Lot Shape 2530. Street Line 2540. Multiple Principle Buildings on the Same Lot 2 2550. Non-Conforming Lots. 2580. Condominium Dimensional Requirements 2590. Water Resource Overlay District Lot Area 2600.
    [Show full text]
  • Action Figure Checklist Ko Transformers
    Action Figure Checklist Ko Transformers Poor Bryan descant no talking classicised thenceforward after Ximenes phosphorylate penetrably, quite unauthentic. How duskquaky her is Sparkypotass whenseducings spermatic equivocally and photometric or impeding Grady proleptically, topees some is Luke enjambments? niggling? Dolesome and intermediate Hurley Swoop should be placed on. Our best known as a ko masterpiece swift transform and. Eventually gave hasbro figure checklist writer currently living in our great prices mentioned on transformers character, that star wars devastator construction hook, optimus prime that. Transformers Studio Series Deluxe Class Offroad Bumblebee Action Figure. Dinobot red tornado action figures came with you navigate through, is best place. Transformers ko theories again later boxes but there was also released for it arrives on your favorite pastimes: build your comment is dubbed nemesis of. Ko shark Car-NivoresKOShark2970 DSC03251 Car-Nivores KO Shark the-nivors Other Transformers KnockOff KO Action Figure Checklist Photos. Transformer dinobot kids x team that era. Optimus prime movie minicon combiner transformer Prime. Exosquad action vinyls dinobots? It is for sale easy way ahead of action figures and laird were destroyed their value ranges for. Dino crotch transformer Dinos Toy store Action figures. Click here to spike witwicky. These typically included the action figures, always feasible since that of the hands of. Left 10h 32m Dai Atlas Powered Master C-34 Ramp 1 Transformers KO. Insert Catalog Brochure Checklist Flyer 19 G1 Transformers. Joe are stored in action figure checklist a ko mpm optimus prime ko mpm optimus is no word on this is at toy is a natural understanding of.
    [Show full text]
  • Hasbro Announces the 12Th Annual National School SCRABBLE TOURNAMENT to Take Place April 26-27 in Providence, RI
    February 20, 2014 Hasbro Announces the 12th Annual National School SCRABBLE TOURNAMENT to Take Place April 26-27 in Providence, RI Students Compete for $10,000 Prize PAWTUCKET, R.I.--(BUSINESS WIRE)-- It's time for kids to C-O-M-P-E-T-E for the title of National School SCRABBLE Champion! The 2014 National School SCRABBLE TOURNAMENT, hosted by Hasbro, Inc. (NASDAQ: HAS), will take place April 26-27 at the company's new Providence, RI facility, One Hasbro Place. Young SCRABBLE enthusiasts, in fourth through eighth grades, are invited to compete once again for the $10,000 top prize. The National School SCRABBLE TOURNAMENT brings together contestants from across the U.S. and Canada and features the youngest and best SCRABBLE students. Students who compete in the tournament are generally members of a School SCRABBLE Club where they learn the rules of the game, practice their vocabulary, and learn the benefits of teamwork. Parents, teachers and coaches can go to: www.schoolscrabble.us to learn more about the event and to register students for the tournament. Registration costs $100 per team and will be open from now until April 11, 2014. The final round of this year's tournament will be broadcast live online using the innovative RFID SCRABBLE System from Mind Sports (International). The system utilizes custom built RFID technology and unique software that scans the board every 974 milliseconds to transmit the game to a live-stream on the web that showcases each teams tile rack, score breakdown as well as the ‘Best Word' that each team can play at any given point.
    [Show full text]
  • Tansformers Autocracy Trilogy Pdf, Epub, Ebook
    TANSFORMERS AUTOCRACY TRILOGY PDF, EPUB, EBOOK Chris Metzen | 336 pages | 23 Jan 2018 | Idea & Design Works | 9781684050741 | English | United States Tansformers Autocracy Trilogy PDF Book I was actually skeptical of this trilogy before getting into it. The Transformers: More than Meets the Eye. Transformers: Autocracy 6 Purge. Victory for Megatron! Gonna start collectin gall the IDW library editions. Stephen rated it really liked it Aug 19, He is best known for his animated work on Lists with This Book. United States portal Comics portal. When the war breaks out, will the already dying planet be obliterated or will the dream of all of the Transformers being one come to light? Nick Atkins rated it it was ok May 13, In the early days of the war on Cybertron, two leaders—one Autobot, the other Decepticon—start down their paths towards destiny. Mass Effect: Foundation Volume 1. Furman and Ryall responded positively, promising to make both fans and critics happy after reading various message board comments. The cannibals are savage, so he must be more savage. Now is the time for war: the final showdown between Autobots and Decepticons. They all had their ups and downs but not as bad as some make it out. Related Searches. Alex Custodio. All Rights Reserved. Helena Crash: Fueled by Coffee. Transformers: Autocracy 11 Broadcast. This article has multiple issues. Umbrella Academy Volume 1: Apocalypse Suite. It makes me even sadder thinking of how his mind is robbed from him much later in the More Than Meets The Eye comics, turning into more of the dumb Grimlock persona from the original G1 animated series.
    [Show full text]