DOCSLIB.ORG

Circular Motionmotion AAA Powerpointpowerpointpowerpoint Presentationpresentationpresentation Bybyby Paulpaulpaul E.E.E

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Circular Motionmotion AAA Powerpointpowerpointpowerpoint Presentationpresentationpresentation Bybyby Paulpaulpaul E.E.E ChapterChapter 10.10. UniformUniform CircularCircular MotionMotion AAA PowerPointPowerPointPowerPoint PresentationPresentationPresentation bybyby PaulPaulPaul E.E.E. Tippens,Tippens,Tippens, ProfessorProfessorProfessor ofofof PhysicsPhysicsPhysics SouthernSouthernSouthern PolytechnicPolytechnicPolytechnic StateStateState UniversityUniversityUniversity © 2007 Centripetal forces keep these children moving in a circular path. Objectives:Objectives: AfterAfter completingcompleting thisthis module,module, youyou shouldshould bebe ableable to:to: •• ApplyApply youryour knowledgeknowledge ofof centripetalcentripetal accelerationacceleration andand centripetalcentripetal forceforce toto thethe solutionsolution ofof problemsproblems inin circularcircular motion.motion. •• DefineDefine andand applyapply conceptsconcepts ofof frequencyfrequency andand period,period, andand relaterelate themthem toto linearlinear speed.speed. •• SolveSolve problemsproblems involvinginvolving bankingbanking angles,angles, thethe conicalconical pendulum,pendulum, andand thethe verticalvertical circle.circle. UniformUniform CircularCircular MotionMotion UniformUniform circularcircular motionmotion is motion along a circular path in which there is no change in speed, only a change in direction. v Constant velocity Fc tangent to path. Constant force toward center. Question: Is there an outward force on the ball? UniformUniform CircularCircular MotionMotion (Cont.)(Cont.) TheThe questionquestion ofof anan outwardoutward forceforce cancan bebe resolvedresolved byby askingasking whatwhat happenshappens whenwhen thethe stringstring breaks!breaks! BallBall movesmoves tangenttangent toto v path,path, NOTNOT outwardoutward asas mightmight bebe expected.expected. When central force is removed, ball continues in straight line. CentripetalCentripetal forceforce isis neededneeded toto changechange direction.direction. ExamplesExamples ofof CentripetalCentripetal ForceForce YouYouYou areareare sittingsittingsitting ononon thethethe seatseatseat nextnextnext tototo thethethe outsideoutsideoutside door.door.door. WhatWhatWhat isisis thethethe directiondirectiondirection ofofof thethethe resultantresultantresultant forceforceforce ononon youyouyou asasas youyouyou turn?turn?turn? IsIsIs ititit awayawayaway fromfromfrom centercentercenter ororor towardtowardtoward centercentercenter ofofof thethethe turn?turn?turn? •• CarCar goinggoing aroundaround aa FF c curve.curve. ForceForce ONON youyou isis towardtoward thethe center.center. CarCar ExampleExample ContinuedContinued Reaction F’ TheThe centripetalcentripetal Fc forceforce isis exertedexerted BYBY thethe doordoor ONON you.you. (Centrally)(Centrally) ThereThereThere isisis ananan outwardoutwardoutward force,force,force, butbutbut ititit doesdoesdoes notnotnot actactact ONONON you.you.you. ItItIt isisis thethethe reactionreactionreaction forceforceforce exertedexertedexerted BYBYBY youyouyou ONONON thethethe door.door.door. ItItIt affectsaffectsaffects onlyonlyonly thethethe door.door.door. AnotherAnother ExampleExample DisappearingDisappearing RR platformplatform atat fair.fair. FF c WhatWhat exertsexerts thethe centripetalcentripetal forceforce inin thisthis exampleexample andand onon whatwhat doesdoes itit act?act? TheTheThe centripetalcentripetalcentripetal forceforceforce isisis exertedexertedexerted BYBYBY thethethe wallwallwall ONONON thethethe man.man.man. AAA reactionreactionreaction forceforceforce isisis exertedexertedexerted bybyby thethethe manmanman ononon thethethe wall,wall,wall, butbutbut thatthatthat doesdoesdoes notnotnot determinedeterminedetermine thethethe motionmotionmotion ofofof thethethe man.man.man. SpinSpin CycleCycle onon aa WasherWasher HowHow isis thethe waterwater removedremoved fromfrom clothesclothes duringduring thethe spinspin cyclecycle ofof aa washer?washer? ThinkThink carefullycarefully beforebefore answeringanswering .. .. .. DoesDoes thethe centripetalcentripetal forceforce throwthrow waterwater offoff thethe clothes?clothes? NO.NO.NO. Actually,Actually,Actually, ititit isisis thethethe LACKLACKLACK ofofof aaa forceforceforce thatthatthat allowsallowsallows thethethe waterwaterwater tototo leaveleaveleave thethethe clothesclothesclothes throughthroughthrough holesholesholes ininin thethethe circularcircularcircular wallwallwall ofofof thethethe rotatingrotatingrotating washer.washer.washer. CentripetalCentripetal AccelerationAcceleration ConsiderConsider ballball movingmoving atat constantconstant speedspeed vv inin aa horizontalhorizontal circlecircle ofof radiusradius RR atat endend ofof stringstring tiedtied toto pegpeg onon centercenter ofof table.table. (Assume(Assume zerozero friction.)friction.) n Fc v W R ForceForce FF c andand accelerationacceleration aac towardtoward center.center. WW == nn DerivingDeriving CentralCentral AccelerationAcceleration Consider initial velocity at A and final velocity at B: vf vf B -vo v s v vo o R R A DerivingDeriving AccelerationAcceleration (Cont.)(Cont.) v v f Definition: ac = -v t o v s vo Similar v s R = Triangles v R mass m v vs vv a = = = c t Rt R Centripetal vm22v Centripetal aFma; acceleration:acceleration: cccR R ExampleExample 1:1: AA 33--kgkg rockrock swingsswings inin aa circlecircle ofof radiusradius 55 mm.. IfIf itsits constantconstant speedspeed isis 88 m/sm/s,, whatwhat isis thethe centripetalcentripetal acceleration?acceleration? v v2 m a m = 3 kg c R R R = 5 m; v = 8 m/s (8 m/s)2 a 12.8 m/s2 c 5 m F = (3 kg)(12.8 m/s2) mv2 Fmacc F = 38.4 N R Fcc = 38.4 N ExampleExample 2:2: AA skaterskater movesmoves withwith 1515 m/sm/s inin aa circlecircle ofof radiusradius 3030 mm.. TheThe iceice exertsexerts aa centralcentral forceforce ofof 450450 NN.. WhatWhat isis thethe massmass ofof thethe skater?skater? DrawDraw andand labellabel sketchsketch mv2 FR Fm; c v = 15 m/s c R v2 (450 N)(30 m) Fc R m 2 450 N 30 m (15 m/s) m=? mm == 60.060.0 kgkg Speed skater ExampleExample 3.3. TheThe wallwall exertsexerts aa 600600 NN forceforce onon anan 8080--kgkg personperson movingmoving atat 44 m/sm/s onon aa circularcircular platform.platform. WhatWhat isis thethe radiusradius ofof thethe circularcircular path?path? DrawDraw andand labellabel sketchsketch NewtonNewton’’ss 2nd2nd lawlaw m = 80 kg; forfor circularcircular motion:motion: v = 4 m/s2 F = 600 N mv22 mv c Fr; rF r = ? (80 kg)(4 m/s)2 r r = 2.13 m 600 N r = 2.13 m CarCar NegotiatingNegotiating aa FlatFlat TurnTurn v FF c R WhatWhat isis thethe directiondirection ofof thethe forceforce ON thethe car?car? Ans.Ans. TowardToward CenterCenter ThisThis centralcentral forceforce isis exertedexerted BYBY thethe roadroad ONON thethe car.car. CarCar NegotiatingNegotiating aa FlatFlat TurnTurn v FF c R IsIs therethere alsoalso anan outwardoutward forceforce actingacting ONON thethe car?car? Ans.Ans. No,No, butbut thethe carcar doesdoes exertexert aa outwardoutward reactionreaction forceforce ONON thethe road.road. CarCar NegotiatingNegotiating aa FlatFlat TurnTurn TheThe centripetalcentripetal forceforce FF c isis thatthat ofof staticstatic frictionfriction ff s :: n F = f Fc R c s m fs v R mg TheThe centralcentral forceforce FF andand thethe frictionfriction forceforce ff The central force FCC and the friction force fss areareare notnotnot twotwotwo differentdifferentdifferent forcesforcesforces thatthatthat areareare equal.equal.equal. ThereThereThere isisis justjustjust oneoneoneforceforce force ononon thethethe car.car.car. TheTheThe naturenaturenature ofofof thisthisthis centralcentralcentral forceforceforce isisis staticstaticstatic friction.friction.friction. FindingFinding thethe maximummaximum speedspeed forfor negotiatingnegotiating aa turnturn withoutwithout slipping.slipping. n Fc = fs fs Fc R R m v mg TheThe carcar isis onon thethe vergeverge ofof slippingslipping whenwhen FF C isis equalequal toto thethe maximummaximum forceforce ofof staticstatic frictionfriction ff s. mv2 f = mg Fc = fs Fc = s s R MaximumMaximum speedspeed withoutwithout slippingslipping (Cont.)(Cont.) F = f n c s fs R mv2 = smg R mg v = sgR F m c R VelocityVelocity vv isis maximummaximum v speedspeed forfor nono slipping.slipping. ExampleExample 4:4: AA carcar negotiatesnegotiates aa turnturn ofof radiusradius 7070 mm whenwhen thethe coefficientcoefficient ofof staticstatic frictionfriction isis 0.70.7.. WhatWhat isis thethe maximummaximum speedspeed toto avoidavoid slipping?slipping? mv2 Fc = fs = s mg m R Fc R From which: v = sgR v s = 0.7 g = 9.8 m/s2; R = 70 m v = 21.9 m/s vgRs (0.7)(9.8)(70m) v = 21.9 m/s OptimumOptimum BankingBanking AngleAngle ByBy bankingbanking aa curvecurve atat thethe optimumoptimum angle,angle, thethe normalnormal F m c R forceforce nn cancan provideprovide thethe necessarynecessary centripetalcentripetal forceforce v withoutwithout thethe needneed forfor aa frictionfriction force.force. f fs = 0 s n n n f w s w w slowslow speedspeed fastfast speedspeed optimumoptimum FreeFree--bodybody DiagramDiagram n AccelerationAcceleration aa isis towardtoward thethe xx center.center. SetSet xx axisaxis alongalong thethe directiondirection ofof aac ,, i.i. e.,e., mg horizontalhorizontal (left(left toto right).right). nn coscos nn nn ++ aac nn sinsin mgmg mgmg OptimumOptimum BankingBanking AngleAngle (Cont.)(Cont.) nn coscos n n nn sinsin mg mgmg ApplyApply mvmv2 FF == mmaa nn sinsin NewtonNewton’’ss 2nd2nd x c RR LawLaw toto xx andand yy axes.axes. FF y == 00 nn coscos == mgmg OptimumOptimum BankingBanking AngleAngle (Cont.)(Cont.) n cos n n nsin tan n sin ncos mg mg mv2
Load more

Recommended publications
  • Rotational Motion (The Dynamics of a Rigid Body)
    University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln Robert Katz Publications Research Papers in Physics and Astronomy 1-1958 Physics, Chapter 11: Rotational Motion (The Dynamics of a Rigid Body) Henry Semat City College of New York Robert Katz University of Nebraska-Lincoln, [email protected] Follow this and additional works at: https://digitalcommons.unl.edu/physicskatz Part of the Physics Commons Semat, Henry and Katz, Robert, "Physics, Chapter 11: Rotational Motion (The Dynamics of a Rigid Body)" (1958). Robert Katz Publications. 141. https://digitalcommons.unl.edu/physicskatz/141 This Article is brought to you for free and open access by the Research Papers in Physics and Astronomy at DigitalCommons@University of Nebraska - Lincoln. It has been accepted for inclusion in Robert Katz Publications by an authorized administrator of DigitalCommons@University of Nebraska - Lincoln. 11 Rotational Motion (The Dynamics of a Rigid Body) 11-1 Motion about a Fixed Axis The motion of the flywheel of an engine and of a pulley on its axle are examples of an important type of motion of a rigid body, that of the motion of rotation about a fixed axis. Consider the motion of a uniform disk rotat­ ing about a fixed axis passing through its center of gravity C perpendicular to the face of the disk, as shown in Figure 11-1. The motion of this disk may be de­ scribed in terms of the motions of each of its individual particles, but a better way to describe the motion is in terms of the angle through which the disk rotates.
    [Show full text]
  • L-9 Conservation of Energy, Friction and Circular Motion Kinetic Energy Potential Energy Conservation of Energy Amusement Pa
    L-9 Conservation of Energy, Friction and Circular Motion Kinetic energy • If something moves in • Kinetic energy, potential energy and any way, it has conservation of energy kinetic energy • kinetic energy (KE) • What is friction and what determines how is energy of motion m v big it is? • If I drive my car into a • Friction is what keeps our cars moving tree, the kinetic energy of the car can • What keeps us moving in a circular path? do work on the tree – KE = ½ m v2 • centripetal vs. centrifugal force it can knock it over KE does not depend on which direction the object moves Potential energy conservation of energy • If I raise an object to some height (h) it also has • if something has energy W stored as energy – potential energy it doesn’t loose it GPE = mgh • If I let the object fall it can do work • It may change from one • We call this Gravitational Potential Energy form to another (potential to kinetic and F GPE= m x g x h = m g h back) h • KE + PE = constant mg mg m in kg, g= 10m/s2, h in m, GPE in Joules (J) • example – roller coaster • when we do work in W=mgh PE regained • the higher I lift the object the more potential lifting the object, the as KE energy it gas work is stored as • example: pile driver, spring launcher potential energy. Amusement park physics Up and down the track • the roller coaster is an excellent example of the conversion of energy from one form into another • work must first be done in lifting the cars to the top of the first hill.
    [Show full text]
  • Multidisciplinary Design Project Engineering Dictionary Version 0.0.2
    Multidisciplinary Design Project Engineering Dictionary Version 0.0.2 February 15, 2006 . DRAFT Cambridge-MIT Institute Multidisciplinary Design Project This Dictionary/Glossary of Engineering terms has been compiled to compliment the work developed as part of the Multi-disciplinary Design Project (MDP), which is a programme to develop teaching material and kits to aid the running of mechtronics projects in Universities and Schools. The project is being carried out with support from the Cambridge-MIT Institute undergraduate teaching programe. For more information about the project please visit the MDP website at http://www-mdp.eng.cam.ac.uk or contact Dr. Peter Long Prof. Alex Slocum Cambridge University Engineering Department Massachusetts Institute of Technology Trumpington Street, 77 Massachusetts Ave. Cambridge. Cambridge MA 02139-4307 CB2 1PZ. USA e-mail: [email protected] e-mail: [email protected] tel: +44 (0) 1223 332779 tel: +1 617 253 0012 For information about the CMI initiative please see Cambridge-MIT Institute website :- http://www.cambridge-mit.org CMI CMI, University of Cambridge Massachusetts Institute of Technology 10 Miller’s Yard, 77 Massachusetts Ave. Mill Lane, Cambridge MA 02139-4307 Cambridge. CB2 1RQ. USA tel: +44 (0) 1223 327207 tel. +1 617 253 7732 fax: +44 (0) 1223 765891 fax. +1 617 258 8539 . DRAFT 2 CMI-MDP Programme 1 Introduction This dictionary/glossary has not been developed as a definative work but as a useful reference book for engi- neering students to search when looking for the meaning of a word/phrase. It has been compiled from a number of existing glossaries together with a number of local additions.
    [Show full text]
  • Two Worked out Examples of Rotations Using Quaternions
    TWO WORKED OUT EXAMPLES OF ROTATIONS USING QUATERNIONS This note is an attachment to the article \Rotations and Quaternions" which in turn is a companion to the video of the talk by the same title. Example 1. Determine the image of the point (1; −1; 2) under the rotation by an angle of 60◦ about an axis in the yz-plane that is inclined at an angle of 60◦ to the positive y-axis. p ◦ ◦ 1 3 Solution: The unit vector u in the direction of the axis of rotation is cos 60 j + sin 60 k = 2 j + 2 k. The quaternion (or vector) corresponding to the point p = (1; −1; 2) is of course p = i − j + 2k. To find −1 θ θ the image of p under the rotation, we calculate qpq where q is the quaternion cos 2 + sin 2 u and θ the angle of rotation (60◦ in this case). The resulting quaternion|if we did the calculation right|would have no constant term and therefore we can interpret it as a vector. That vector gives us the answer. p p p p p We have q = 3 + 1 u = 3 + 1 j + 3 k = 1 (2 3 + j + 3k). Since q is by construction a unit quaternion, 2 2 2 4 p4 4 p −1 1 its inverse is its conjugate: q = 4 (2 3 − j − 3k). Now, computing qp in the routine way, we get 1 p p p p qp = ((1 − 2 3) + (2 + 3 3)i − 3j + (4 3 − 1)k) 4 and then another long but routine computation gives 1 p p p qpq−1 = ((10 + 4 3)i + (1 + 2 3)j + (14 − 3 3)k) 8 The point corresponding to the vector on the right hand side in the above equation is the image of (1; −1; 2) under the given rotation.
    [Show full text]
  • Circular Motion Dynamics
    Circular Motion Dynamics 8.01 W04D2 Today’s Reading Assignment: MIT 8.01 Course Notes Chapter 9 Circular Motion Dynamics Sections 9.1-9.2 Announcements Problem Set 3 due Week 5 Tuesday at 9 pm in box outside 26-152 Math Review Week 5 Tuesday 9-11 pm in 26-152. Next Reading Assignment (W04D3): MIT 8.01 Course Notes Chapter 9 Circular Motion Dynamics Section 9.3 Circular Motion: Vector Description Position r(t) r rˆ(t) = Component of Angular ω ≡ dθ / dt Velocity z Velocity v = v θˆ(t) = r(dθ / dt) θˆ θ Component of Angular 2 2 α ≡ dω / dt = d θ / dt Acceleration z z a = a rˆ + a θˆ Acceleration r θ a = −r(dθ / dt)2 = −(v2 / r), a = r(d 2θ / dt 2 ) r θ Concept Question: Car in a Turn You are a passenger in a racecar approaching a turn after a straight-away. As the car turns left on the circular arc at constant speed, you are pressed against the car door. Which of the following is true during the turn (assume the car doesn't slip on the roadway)? 1. A force pushes you away from the door. 2. A force pushes you against the door. 3. There is no force that pushes you against the door. 4. The frictional force between you and the seat pushes you against the door. 5. There is no force acting on you. 6. You cannot analyze this situation in terms of the forces on you since you are accelerating. 7. Two of the above.
    [Show full text]
  • Circular Motion and Newton's Law of Gravitation
    CIRCULAR MOTION AND NEWTON’S LAW OF GRAVITATION I. Speed and Velocity Speed is distance divided by time…is it any different for an object moving around a circle? The distance around a circle is C = 2πr, where r is the radius of the circle So average speed must be the circumference divided by the time to get around the circle once C 2πr one trip around the circle is v = = known as the period. We’ll use T T big T to represent this time SINCE THE SPEED INCREASES WITH RADIUS, CAN YOU VISUALIZE THAT IF YOU WERE SITTING ON A SPINNING DISK, YOU WOULD SPEED UP IF YOU MOVED CLOSER TO THE OUTER EDGE OF THE DISK? 1 These four dots each make one revolution around the disk in the same time, but the one on the edge goes the longest distance. It must be moving with a greater speed. Remember velocity is a vector. The direction of velocity in circular motion is on a tangent to the circle. The direction of the vector is ALWAYS changing in circular motion. 2 II. ACCELERATION If the velocity vector is always changing EQUATIONS: in circular motion, THEN AN OBJECT IN CIRCULAR acceleration in circular MOTION IS ACCELERATING. motion can be written as, THE ACCELERATION VECTOR POINTS v2 INWARD TO THE CENTER OF THE a = MOTION. r Pick two v points on the path. 2 Subtract head to tail…the 4π r v resultant is the change in v or a = 2 f T the acceleration vector vi a a Assignment: check the units -vi and do the algebra to make vf sure you believe these equations Note that the acceleration vector points in 3 III.
    [Show full text]
  • Circular Motion Angular Velocity
    PHY131H1F - Class 8 Quiz time… – Angular Notation: it’s all Today, finishing off Chapter 4: Greek to me! d • Circular Motion dt • Rotation θ is an angle, and the S.I. unit of angle is rad. The time derivative of θ is ω. What are the S.I. units of ω ? A. m/s2 B. rad / s C. N/m D. rad E. rad /s2 Last day I asked at the end of class: Quiz time… – Angular Notation: it’s all • You are driving North Highway Greek to me! d 427, on the smoothly curving part that will join to the Westbound 401. v dt Your speedometer is constant at 115 km/hr. Your steering wheel is The time derivative of ω is α. not rotating, but it is turned to the a What are the S.I. units of α ? left to follow the curve of the A. m/s2 highway. Are you accelerating? B. rad / s • ANSWER: YES! Any change in velocity, either C. N/m magnitude or speed, implies you are accelerating. D. rad • If so, in what direction? E. rad /s2 • ANSWER: West. If your speed is constant, acceleration is always perpendicular to the velocity, toward the centre of circular path. Circular Motion r = constant Angular Velocity s and θ both change as the particle moves s = “arc length” θ = “angular position” when θ is measured in radians when ω is measured in rad/s 1 Special case of circular motion: Uniform Circular Motion A carnival has a Ferris wheel where some seats are located halfway between the center Tangential velocity is and the outside rim.
    [Show full text]
  • Trigonometric Functions
    72 Chapter 4 Trigonometric Functions To define the radian measurement system, we consider the unit circle in the xy-plane: ........................ ....... ....... ...... ....................... .............. ............... ......... ......... ....... ....... ....... ...... ...... ...... ..... ..... ..... ..... ..... ..... .... ..... ..... .... .... .... .... ... (cos x, sin x) ... ... 4 ... A ..... .. ... ....... ... ... ....... ... .. ....... .. .. ....... .. .. ....... .. .. ....... .. .. ....... .. .. ....... ...... ....... ....... ...... ....... x . ....... Trigonometric Functions . ...... ....y . ....... (1, 0) . ....... ....... .. ...... .. .. ....... .. .. ....... .. .. ....... .. .. ....... .. ... ...... ... ... ....... ... ... .......... ... ... ... ... .... B... .... .... ..... ..... ..... ..... ..... ..... ..... ..... ...... ...... ...... ...... ....... ....... ........ ........ .......... .......... ................................................................................... An angle, x, at the center of the circle is associated with an arc of the circle which is said to subtend the angle. In the figure, this arc is the portion of the circle from point (1, 0) So far we have used only algebraic functions as examples when finding derivatives, that is, to point A. The length of this arc is the radian measure of the angle x; the fact that the functions that can be built up by the usual algebraic operations of addition, subtraction, radian measure is an actual geometric length is largely responsible for the usefulness of
    [Show full text]
  • Rotational Motion and Angular Momentum 317
    CHAPTER 10 | ROTATIONAL MOTION AND ANGULAR MOMENTUM 317 10 ROTATIONAL MOTION AND ANGULAR MOMENTUM Figure 10.1 The mention of a tornado conjures up images of raw destructive power. Tornadoes blow houses away as if they were made of paper and have been known to pierce tree trunks with pieces of straw. They descend from clouds in funnel-like shapes that spin violently, particularly at the bottom where they are most narrow, producing winds as high as 500 km/h. (credit: Daphne Zaras, U.S. National Oceanic and Atmospheric Administration) Learning Objectives 10.1. Angular Acceleration • Describe uniform circular motion. • Explain non-uniform circular motion. • Calculate angular acceleration of an object. • Observe the link between linear and angular acceleration. 10.2. Kinematics of Rotational Motion • Observe the kinematics of rotational motion. • Derive rotational kinematic equations. • Evaluate problem solving strategies for rotational kinematics. 10.3. Dynamics of Rotational Motion: Rotational Inertia • Understand the relationship between force, mass and acceleration. • Study the turning effect of force. • Study the analogy between force and torque, mass and moment of inertia, and linear acceleration and angular acceleration. 10.4. Rotational Kinetic Energy: Work and Energy Revisited • Derive the equation for rotational work. • Calculate rotational kinetic energy. • Demonstrate the Law of Conservation of Energy. 10.5. Angular Momentum and Its Conservation • Understand the analogy between angular momentum and linear momentum. • Observe the relationship between torque and angular momentum. • Apply the law of conservation of angular momentum. 10.6. Collisions of Extended Bodies in Two Dimensions • Observe collisions of extended bodies in two dimensions. • Examine collision at the point of percussion.
    [Show full text]
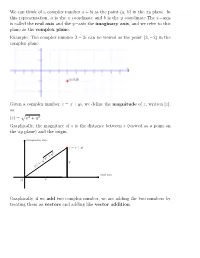
  • We Can Think of a Complex Number a + Bi As the Point (A, B) in the Xy Plane
    We can think of a complex number a + bi as the point (a, b) in the xy plane. In this representation, a is the x coordinate and b is the y coordinate.The x−axis is called the real axis and the y−axis the imaginary axis, and we refer to this plane as the complex plane. Example: The complex number 3 − 2i can be viewed as the point (3; −2) in the complex plane. Given a complex number z = x + yi, we define the magnitude of z, written jzj, as: jzj = px2 + y2. Graphically, the magniture of z is the distance between z (viewed as a point on the xy plane) and the origin. imaginary axis z = x + yi 2 y 2 + x p y j = jz real axis O x Graphically, if we add two complex number, we are adding the two numbers by treating them as vectors and adding like vector addition. For example, Let z = 5 + 2i, w = 1 + 6i, then z + w = (5 + 2i) + (1 + 6i) = (5 + 1) + (2 + 6)i = 6 + 8i In order to interpret multiplication of two complex numbers, let's look again at the complex number represented as a point on the complex plane. This time, we let r = px2 + y2 be the magnitude of z. Let 0 ≤ θ < 2π be the angle in standard position with z being its terminal point. We call θ the argument of the complex number z: imaginary axis imaginary axis z = x + yi z = x + yi 2 y 2 + p x r j = y y jz = r θ real axis θ real axis O x O x By definition of sine and cosine, we have x cos(θ) = ) x = r cos(θ) r y sin(θ) = ) y = r sin(θ) r We have obtained the polar representation of a complex number: Suppose z = x + yi is a complex number with (x; y) in rectangular coordinate.
    [Show full text]
  • Physics 3550, Fall 2012 Two Body, Central-Force Problem Relevant Sections in Text: §8.1 – 8.7
    Two Body, Central-Force Problem. Physics 3550, Fall 2012 Two Body, Central-Force Problem Relevant Sections in Text: x8.1 { 8.7 Two Body, Central-Force Problem { Introduction. I have already mentioned the two body central force problem several times. This is, of course, an important dynamical system since it represents in many ways the most fundamental kind of interaction between two bodies. For example, this interaction could be gravitational { relevant in astrophysics, or the interaction could be electromagnetic { relevant in atomic physics. There are other possibilities, too. For example, a simple model of strong interactions involves two-body central forces. Here we shall begin a systematic study of this dynamical system. As we shall see, the conservation laws admitted by this system allow for a complete determination of the motion. Many of the topics we have been discussing in previous lectures come into play here. While this problem is very instructive and physically quite important, it is worth keeping in mind that the complete solvability of this system makes it an exceptional type of dynamical system. We cannot solve for the motion of a generic system as we do for the two body problem. The two body problem involves a pair of particles with masses m1 and m2 described by a Lagrangian of the form: 1 2 1 2 L = m ~r_ + m ~r_ − V (j~r − ~r j): 2 1 1 2 2 2 1 2 Reflecting the fact that it describes a closed, Newtonian system, this Lagrangian is in- variant under spatial translations, time translations, rotations, and boosts.* Thus we will have conservation of total energy, total momentum and total angular momentum for this system.
    [Show full text]
  • Chapter 4: Circular Motion
    Chapter 4: Circular Motion ! Why do pilots sometimes black out while pulling out at the bottom of a power dive? ! Are astronauts really "weightless" while in orbit? ! Why do you tend to slide across the car seat when the car makes a sharp turn? Make sure you know how to: 1. Find the direction of acceleration using the motion diagram. 2. Draw a force diagram. 3. Use a force diagram to help apply Newton’s second law in component form. CO: Ms. Kruti Patel, a civilian test pilot, wears a special flight suit and practices special breathing techniques to prevent dizziness, disorientation, and possibly passing out as she pulls out of a power dive. This dizziness, or worse, is called a blackout and occurs when there is a lack of blood to the head and brain. Tony Wayne in his book Ride Physiology describes the symptoms of blackout. As the acceleration climbs up toward 7 g , “you … can no longer see color. … An instant later, … your field of vision is shrinking. It now looks like you are seeing things through a pipe. … The visual pipe's diameter is getting smaller and smaller. In a flash you see black. You have just "blacked out." You are unconscious …” Why does blackout occur and why does a special suit prevent blackout? Our study of circular motion in this chapter will help us understand this and other interesting phenomena. Lead In the previous chapters we studied the motion of objects when the sum of the forces exerted on them was constant in terms of magnitude and direction.
    [Show full text]