Cyclotomic Polynomials
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Resultant of the Cyclotomic Polynomials Fm(Ax) and Fn{Bx)
MATHEMATICS OF COMPUTATION, VOLUME 29, NUMBER 129 JANUARY 1975, PAGES 1-6 The Resultant of the Cyclotomic Polynomials Fm(ax) and Fn{bx) By Tom M. Apóstol Abstract. The resultant p(Fm(ax), Fn(bx)) is calculated for arbitrary positive integers m and n, and arbitrary nonzero complex numbers a and b. An addendum gives an extended bibliography of work on cyclotomic polynomials published since 1919. 1. Introduction. Let Fn(x) denote the cyclotomic polynomial of degree sp{ri) given by Fn{x)= f['{x - e2"ikl"), k=\ where the ' indicates that k runs through integers relatively prime to the upper index n, and <p{n) is Euler's totient. The resultant p{Fm, Fn) of any two cyclotomic poly- nomials was first calculated by Emma Lehmer [9] in 1930 and later by Diederichsen [21] and the author [64]. It is known that piFm, Fn) = 1 if (m, ri) = 1, m > n>l. This implies that for any integer q the integers Fmiq) and Fn{q) are rela- tively prime if im, ri) = 1. Divisibility properties of cyclotomic polynomials play a role in certain areas of the theory of numbers, such as the distribution of quadratic residues, difference sets, per- fect numbers, Mersenne-type numbers, and primes in residue classes. There has also been considerable interest lately in relations between the integers FJq) and F Jp), where p and q are distinct primes. In particular, Marshall Hall informs me that the Feit-Thompson proof [47] could be shortened by nearly 50 pages if it were known that F Jq) and F Jp) are relatively prime, or even if the smaller of these integers does not divide the larger. -

08 Cyclotomic Polynomials
8. Cyclotomic polynomials 8.1 Multiple factors in polynomials 8.2 Cyclotomic polynomials 8.3 Examples 8.4 Finite subgroups of fields 8.5 Infinitude of primes p = 1 mod n 8.6 Worked examples 1. Multiple factors in polynomials There is a simple device to detect repeated occurrence of a factor in a polynomial with coefficients in a field. Let k be a field. For a polynomial n f(x) = cnx + ::: + c1x + c0 [1] with coefficients ci in k, define the (algebraic) derivative Df(x) of f(x) by n−1 n−2 2 Df(x) = ncnx + (n − 1)cn−1x + ::: + 3c3x + 2c2x + c1 Better said, D is by definition a k-linear map D : k[x] −! k[x] defined on the k-basis fxng by D(xn) = nxn−1 [1.0.1] Lemma: For f; g in k[x], D(fg) = Df · g + f · Dg [1] Just as in the calculus of polynomials and rational functions one is able to evaluate all limits algebraically, one can readily prove (without reference to any limit-taking processes) that the notion of derivative given by this formula has the usual properties. 115 116 Cyclotomic polynomials [1.0.2] Remark: Any k-linear map T of a k-algebra R to itself, with the property that T (rs) = T (r) · s + r · T (s) is a k-linear derivation on R. Proof: Granting the k-linearity of T , to prove the derivation property of D is suffices to consider basis elements xm, xn of k[x]. On one hand, D(xm · xn) = Dxm+n = (m + n)xm+n−1 On the other hand, Df · g + f · Dg = mxm−1 · xn + xm · nxn−1 = (m + n)xm+n−1 yielding the product rule for monomials. -

Algorithmic Factorization of Polynomials Over Number Fields
Rose-Hulman Institute of Technology Rose-Hulman Scholar Mathematical Sciences Technical Reports (MSTR) Mathematics 5-18-2017 Algorithmic Factorization of Polynomials over Number Fields Christian Schulz Rose-Hulman Institute of Technology Follow this and additional works at: https://scholar.rose-hulman.edu/math_mstr Part of the Number Theory Commons, and the Theory and Algorithms Commons Recommended Citation Schulz, Christian, "Algorithmic Factorization of Polynomials over Number Fields" (2017). Mathematical Sciences Technical Reports (MSTR). 163. https://scholar.rose-hulman.edu/math_mstr/163 This Dissertation is brought to you for free and open access by the Mathematics at Rose-Hulman Scholar. It has been accepted for inclusion in Mathematical Sciences Technical Reports (MSTR) by an authorized administrator of Rose-Hulman Scholar. For more information, please contact [email protected]. Algorithmic Factorization of Polynomials over Number Fields Christian Schulz May 18, 2017 Abstract The problem of exact polynomial factorization, in other words expressing a poly- nomial as a product of irreducible polynomials over some field, has applications in algebraic number theory. Although some algorithms for factorization over algebraic number fields are known, few are taught such general algorithms, as their use is mainly as part of the code of various computer algebra systems. This thesis provides a summary of one such algorithm, which the author has also fully implemented at https://github.com/Whirligig231/number-field-factorization, along with an analysis of the runtime of this algorithm. Let k be the product of the degrees of the adjoined elements used to form the algebraic number field in question, let s be the sum of the squares of these degrees, and let d be the degree of the polynomial to be factored; then the runtime of this algorithm is found to be O(d4sk2 + 2dd3). -

Algebraic Number Theory
Algebraic Number Theory William B. Hart Warwick Mathematics Institute Abstract. We give a short introduction to algebraic number theory. Algebraic number theory is the study of extension fields Q(α1; α2; : : : ; αn) of the rational numbers, known as algebraic number fields (sometimes number fields for short), in which each of the adjoined complex numbers αi is algebraic, i.e. the root of a polynomial with rational coefficients. Throughout this set of notes we use the notation Z[α1; α2; : : : ; αn] to denote the ring generated by the values αi. It is the smallest ring containing the integers Z and each of the αi. It can be described as the ring of all polynomial expressions in the αi with integer coefficients, i.e. the ring of all expressions built up from elements of Z and the complex numbers αi by finitely many applications of the arithmetic operations of addition and multiplication. The notation Q(α1; α2; : : : ; αn) denotes the field of all quotients of elements of Z[α1; α2; : : : ; αn] with nonzero denominator, i.e. the field of rational functions in the αi, with rational coefficients. It is the smallest field containing the rational numbers Q and all of the αi. It can be thought of as the field of all expressions built up from elements of Z and the numbers αi by finitely many applications of the arithmetic operations of addition, multiplication and division (excepting of course, divide by zero). 1 Algebraic numbers and integers A number α 2 C is called algebraic if it is the root of a monic polynomial n n−1 n−2 f(x) = x + an−1x + an−2x + ::: + a1x + a0 = 0 with rational coefficients ai. -

20. Cyclotomic III
20. Cyclotomic III 20.1 Prime-power cyclotomic polynomials over Q 20.2 Irreducibility of cyclotomic polynomials over Q 20.3 Factoring Φn(x) in Fp[x] with pjn 20.4 Worked examples The main goal is to prove that all cyclotomic polynomials Φn(x) are irreducible in Q[x], and to see what happens to Φn(x) over Fp when pjn. The irreducibility over Q allows us to conclude that the automorphism group of Q(ζn) over Q (with ζn a primitive nth root of unity) is × Aut(Q(ζn)=Q) ≈ (Z=n) by the map a (ζn −! ζn) − a The case of prime-power cyclotomic polynomials in Q[x] needs only Eisenstein's criterion, but the case of general n seems to admit no comparably simple argument. The proof given here uses ideas already in hand, but also an unexpected trick. We will give a different, less elementary, but possibly more natural argument later using p-adic numbers and Dirichlet's theorem on primes in an arithmetic progression. 1. Prime-power cyclotomic polynomials over Q The proof of the following is just a slight generalization of the prime-order case. [1.0.1] Proposition: For p prime and for 1 ≤ e 2 Z the prime-power pe-th cyclotomic polynomial Φpe (x) is irreducible in Q[x]. Proof: Not unexpectedly, we use Eisenstein's criterion to prove that Φpe (x) is irreducible in Z[x], and the invoke Gauss' lemma to be sure that it is irreducible in Q[x]. Specifically, let f(x) = Φpe (x + 1) 269 270 Cyclotomic III p If e = 1, we are in the familiar prime-order case. -

The Nth Root of a Number Page 1
Lecture Notes The nth Root of a Number page 1 Caution! Currently, square roots are dened differently in different textbooks. In conversations about mathematics, approach the concept with caution and rst make sure that everyone in the conversation uses the same denition of square roots. Denition: Let A be a non-negative number. Then the square root of A (notation: pA) is the non-negative number that, if squared, the result is A. If A is negative, then pA is undened. For example, consider p25. The square-root of 25 is a number, that, when we square, the result is 25. There are two such numbers, 5 and 5. The square root is dened to be the non-negative such number, and so p25 is 5. On the other hand, p 25 is undened, because there is no real number whose square, is negative. Example 1. Evaluate each of the given numerical expressions. a) p49 b) p49 c) p 49 d) p 49 Solution: a) p49 = 7 c) p 49 = unde ned b) p49 = 1 p49 = 1 7 = 7 d) p 49 = 1 p 49 = unde ned Square roots, when stretched over entire expressions, also function as grouping symbols. Example 2. Evaluate each of the following expressions. a) p25 p16 b) p25 16 c) p144 + 25 d) p144 + p25 Solution: a) p25 p16 = 5 4 = 1 c) p144 + 25 = p169 = 13 b) p25 16 = p9 = 3 d) p144 + p25 = 12 + 5 = 17 . Denition: Let A be any real number. Then the third root of A (notation: p3 A) is the number that, if raised to the third power, the result is A. -

Math Symbol Tables
APPENDIX A I Math symbol tables A.I Hebrew letters Type: Print: Type: Print: \aleph ~ \beth :J \daleth l \gimel J All symbols but \aleph need the amssymb package. 346 Appendix A A.2 Greek characters Type: Print: Type: Print: Type: Print: \alpha a \beta f3 \gamma 'Y \digamma F \delta b \epsilon E \varepsilon E \zeta ( \eta 'f/ \theta () \vartheta {) \iota ~ \kappa ,.. \varkappa x \lambda ,\ \mu /-l \nu v \xi ~ \pi 7r \varpi tv \rho p \varrho (} \sigma (J \varsigma <; \tau T \upsilon v \phi ¢ \varphi 'P \chi X \psi 'ljJ \omega w \digamma and \ varkappa require the amssymb package. Type: Print: Type: Print: \Gamma r \varGamma r \Delta L\ \varDelta L.\ \Theta e \varTheta e \Lambda A \varLambda A \Xi ~ \varXi ~ \Pi II \varPi II \Sigma 2: \varSigma E \Upsilon T \varUpsilon Y \Phi <I> \varPhi t[> \Psi III \varPsi 1ft \Omega n \varOmega D All symbols whose name begins with var need the amsmath package. Math symbol tables 347 A.3 Y1EX binary relations Type: Print: Type: Print: \in E \ni \leq < \geq >'" \11 « \gg \prec \succ \preceq \succeq \sim \cong \simeq \approx \equiv \doteq \subset c \supset \subseteq c \supseteq \sqsubseteq c \sqsupseteq \smile \frown \perp 1- \models F \mid I \parallel II \vdash f- \dashv -1 \propto <X \asymp \bowtie [Xl \sqsubset \sqsupset \Join The latter three symbols need the latexsym package. 348 Appendix A A.4 AMS binary relations Type: Print: Type: Print: \leqs1ant :::::; \geqs1ant ): \eqs1ant1ess :< \eqs1antgtr :::> \lesssim < \gtrsim > '" '" < > \lessapprox ~ \gtrapprox \approxeq ~ \lessdot <:: \gtrdot Y \111 «< \ggg »> \lessgtr S \gtr1ess Z < >- \lesseqgtr > \gtreq1ess < > < \gtreqq1ess \lesseqqgtr > < ~ \doteqdot --;- \eqcirc = .2.. -

Number Theory and Graph Theory Chapter 3 Arithmetic Functions And
1 Number Theory and Graph Theory Chapter 3 Arithmetic functions and roots of unity By A. Satyanarayana Reddy Department of Mathematics Shiv Nadar University Uttar Pradesh, India E-mail: [email protected] 2 Module-4: nth roots of unity Objectives • Properties of nth roots of unity and primitive nth roots of unity. • Properties of Cyclotomic polynomials. Definition 1. Let n 2 N. Then, a complex number z is called 1. an nth root of unity if it satisfies the equation xn = 1, i.e., zn = 1. 2. a primitive nth root of unity if n is the smallest positive integer for which zn = 1. That is, zn = 1 but zk 6= 1 for any k;1 ≤ k ≤ n − 1. 2pi zn = exp( n ) is a primitive n-th root of unity. k • Note that zn , for 0 ≤ k ≤ n − 1, are the n distinct n-th roots of unity. • The nth roots of unity are located on the unit circle of the complex plane, and in that plane they form the vertices of an n-sided regular polygon with one vertex at (1;0) and centered at the origin. The following points are collected from the article Cyclotomy and cyclotomic polynomials by B.Sury, Resonance, 1999. 1. Cyclotomy - literally circle-cutting - was a puzzle begun more than 2000 years ago by the Greek geometers. In their pastime, they used two implements - a ruler to draw straight lines and a compass to draw circles. 2. The problem of cyclotomy was to divide the circumference of a circle into n equal parts using only these two implements. -
![Monic Polynomials in $ Z [X] $ with Roots in the Unit Disc](https://docslib.b-cdn.net/cover/9626/monic-polynomials-in-z-x-with-roots-in-the-unit-disc-569626.webp)
Monic Polynomials in $ Z [X] $ with Roots in the Unit Disc
MONIC POLYNOMIALS IN Z[x] WITH ROOTS IN THE UNIT DISC Pantelis A. Damianou A Theorem of Kronecker This note is motivated by an old result of Kronecker on monic polynomials with integer coefficients having all their roots in the unit disc. We call such polynomials Kronecker polynomials for short. Let k(n) denote the number of Kronecker polynomials of degree n. We describe a canonical form for such polynomials and use it to determine the sequence k(n), for small values of n. The first step is to show that the number of Kronecker polynomials of degree n is finite. This fact is included in the following theorem due to Kronecker [6]. See also [5] for a more accessible proof. The theorem actually gives more: the non-zero roots of such polynomials are on the boundary of the unit disc. We use this fact later on to show that these polynomials are essentially products of cyclotomic polynomials. Theorem 1 Let λ =06 be a root of a monic polynomial f(z) with integer coefficients. If all the roots of f(z) are in the unit disc {z ∈ C ||z| ≤ 1}, then |λ| =1. Proof Let n = degf. The set of all monic polynomials of degree n with integer coefficients having all their roots in the unit disc is finite. To see this, we write n n n 1 n 2 z + an 1z − + an 2z − + ··· + a0 = (z − zj) , − − j Y=1 where aj ∈ Z and zj are the roots of the polynomial. Using the fact that |zj| ≤ 1 we have: n |an 1| = |z1 + z2 + ··· + zn| ≤ n = − 1 n |an 2| = | zjzk| ≤ − j,k 2! . -
![Arxiv:0709.4112V1 [Math.NT] 26 Sep 2007 H Uhri Pnrdb H Okwgnfoundation](https://docslib.b-cdn.net/cover/6890/arxiv-0709-4112v1-math-nt-26-sep-2007-h-uhri-pnrdb-h-okwgnfoundation-606890.webp)
Arxiv:0709.4112V1 [Math.NT] 26 Sep 2007 H Uhri Pnrdb H Okwgnfoundation
Elle est `atoi cette chanson Toi l’professeur qui sans fa¸con, As ouvert ma petite th`ese Quand mon espoir manquait de braise1. To the memory of Manuel Bronstein CYCLOTOMY PRIMALITY PROOFS AND THEIR CERTIFICATES PREDA MIHAILESCU˘ Abstract. The first efficient general primality proving method was proposed in the year 1980 by Adleman, Pomerance and Rumely and it used Jacobi sums. The method was further developed by H. W. Lenstra Jr. and more of his students and the resulting primality proving algorithms are often referred to under the generic name of Cyclotomy Primality Proving (CPP). In the present paper we give an overview of the theoretical background and implementation specifics of CPP, such as we understand them in the year 2007. Contents 1. Introduction 2 1.1. Some notations 5 2. Galois extensions of rings and cyclotomy 5 2.1. Finding Roots in Cyclotomic Extensions 11 2.2. Finding Roots of Unity and the Lucas – Lehmer Test 12 arXiv:0709.4112v1 [math.NT] 26 Sep 2007 3. GaussandJacobisumsoverCyclotomicExtensionsofRings 14 4. Further Criteria for Existence of Cyclotomic Extensions 17 5. Certification 19 5.1. Computation of Jacobi Sums and their Certification 21 6. Algorithms 23 7. Deterministic primality test 25 8. Asymptotics and run times 29 References 30 1 “Chanson du professeur”, free after G. Brassens Date: Version 2.0 October 26, 2018. The author is sponored by the Volkswagen Foundation. 1 2 PREDA MIHAILESCU˘ 1. Introduction Let n be an integer about which one wishes a decision, whether it is prime or not. The decision may be taken by starting from the definition, thus performing trial division by integers √n or is using some related sieve method, when the decision on a larger set of≤ integers is expected. -

Subclass Discriminant Nonnegative Matrix Factorization for Facial Image Analysis
Pattern Recognition 45 (2012) 4080–4091 Contents lists available at SciVerse ScienceDirect Pattern Recognition journal homepage: www.elsevier.com/locate/pr Subclass discriminant Nonnegative Matrix Factorization for facial image analysis Symeon Nikitidis b,a, Anastasios Tefas b, Nikos Nikolaidis b,a, Ioannis Pitas b,a,n a Informatics and Telematics Institute, Center for Research and Technology, Hellas, Greece b Department of Informatics, Aristotle University of Thessaloniki, Greece article info abstract Article history: Nonnegative Matrix Factorization (NMF) is among the most popular subspace methods, widely used in Received 4 October 2011 a variety of image processing problems. Recently, a discriminant NMF method that incorporates Linear Received in revised form Discriminant Analysis inspired criteria has been proposed, which achieves an efficient decomposition of 21 March 2012 the provided data to its discriminant parts, thus enhancing classification performance. However, this Accepted 26 April 2012 approach possesses certain limitations, since it assumes that the underlying data distribution is Available online 16 May 2012 unimodal, which is often unrealistic. To remedy this limitation, we regard that data inside each class Keywords: have a multimodal distribution, thus forming clusters and use criteria inspired by Clustering based Nonnegative Matrix Factorization Discriminant Analysis. The proposed method incorporates appropriate discriminant constraints in the Subclass discriminant analysis NMF decomposition cost function in order to address the problem of finding discriminant projections Multiplicative updates that enhance class separability in the reduced dimensional projection space, while taking into account Facial expression recognition Face recognition subclass information. The developed algorithm has been applied for both facial expression and face recognition on three popular databases. -
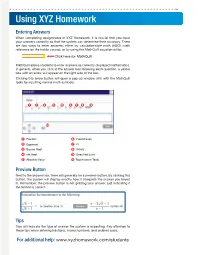
Using XYZ Homework
Using XYZ Homework Entering Answers When completing assignments in XYZ Homework, it is crucial that you input your answers correctly so that the system can determine their accuracy. There are two ways to enter answers, either by calculator-style math (ASCII math reference on the inside covers), or by using the MathQuill equation editor. Click here for MathQuill MathQuill allows students to enter answers as correctly displayed mathematics. In general, when you click in the answer box following each question, a yellow box with an arrow will appear on the right side of the box. Clicking this arrow button will open a pop-up window with with the MathQuill tools for inputting normal math symbols. 1 2 3 4 5 6 7 8 9 10 1 Fraction 6 Parentheses 2 Exponent 7 Pi 3 Square Root 8 Infinity 4 nth Root 9 Does Not Exist 5 Absolute Value 10 Touchscreen Tools Preview Button Next to the answer box, there will generally be a preview button. By clicking this button, the system will display exactly how it interprets the answer you keyed in. Remember, the preview button is not grading your answer, just indicating if the format is correct. Tips Tips will indicate the type of answer the system is expecting. Pay attention to these tips when entering fractions, mixed numbers, and ordered pairs. For additional help: www.xyzhomework.com/students ASCII Math (Calculator Style) Entry Some question types require a mathematical expression or equation in the answer box. Because XYZ Homework follows order of operations, the use of proper grouping symbols is necessary.