DOCSLIB.ORG

Parameterization of Rainfall Microstructure for Radar Meteorology and Hydrology

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Parameterization of Rainfall Microstructure for Radar Meteorology and Hydrology Parameterization of Rainfall Microstructure for Radar Meteorology and Hydrology R. Uijlenhoet Publishedbefor ei nDecembe r 1999a sdoctora lthesi s Rapport 109 Sub-department Water Resources Nieuwe Kanaal 11, 6709 PA Wageningen The Netherlands Internet: www.dow.wau.nl/whh ISSN 0926-230X Remko Uijlenhoet Parameterization of Rainfall Microstructure for Radar Meteorology and Hydrology PROEFSCHRIFT ter verkrijging van de graad van doctor op gezag van de rector magnificus van Wageningen Universiteit, dr. C. M. Karssen, in het openbaar te verdedigen op dinsdag 21 december 1999 des namiddags te vier uur in de Aula. Promotoren: dr. ir. R. A. Feddes hoogleraar bodemnatuurkunde, agrohydrologie en grondwaterbeheer dr. ir. L. P. Ligthart hoogleraar microgolftransmissie, radar en remote sensing technologie Technische Universiteit Delft, International Research Centre for Telecommunications-transmission and Radar Co-promotor: ir. J. N. M. Strieker universitair hoofddocent bij de leerstoelgroep hydrologie en kwantitatief waterbeheer Financial support for the research in this thesis hasbee n provided byth e Commission of the European Communities under the EPOCH and ENVIRONMENT programmes (Contracts No. EPOC-CT90-0026, EV5V-CT92-0182 and ENV4-CT96-5030). Opponenten: prof. dr. ir. J. Grasman, Wageningen Universiteit dr. A. J. Illingworth, University of Reading, Verenigd Koninkrijk prof. dr. J. A. Smith, Princeton University, Verenigde Staten dr. J. Testud, CETP/CNRS, Vélizy, Frankrijk Druk: Universal Press, Veenendaal Foto omslag: Quirin van Os / KNMI CIP-DATA KONINKLIJKE BIBLIOTHEEK, DEN HAAG Uijlenhoet, Remko Parameterization of rainfall microstructure for radar meteorology and hydrology / Remko Uijlenhoet. Doctoral thesis Wageningen University. - With ref. - With summary in Dutch. ISBN 90-5808-156-7 Subject headings: hydrology / meteorology. Financial support for the research in this thesis has been provided by the Commission of the European Communities under the EPOCH and ENVIRONMENT programmes (Contracts No. EPOC-CT90-0026, EV5V-CT92-0182 and ENV4-CT96-5030). Promotoren: dr. ir. R. A. Feddes hoogleraar bodemnatuurkunde, agrohydrologie en grondwaterbeheer dr. ir. L. P. Ligthart hoogleraar microgolftransmissie, radar en remote sensing technologie Technische Universiteit Delft, International Research Centre for Telecommunications-transmission and Radar Co-promotor: ir. J. N. M. Strieker universitair hoofddocent bij de leerstoelgroep hydrologie en kwantitatief waterbeheer Opponenten: prof. dr. ir. J. Grasman, Wageningen Universiteit dr. A. J. Illingworth, University of Reading, Verenigd Koninkrijk prof. dr. J. A. Smith, Princeton University, Verenigde Staten dr. J. Testud, CETP/CNRS, Vélizy, Frankrijk CIP-DATA KONINKLIJKE BIBLIOTHEEK, DEN HAAG Uijlenhoet, Remko Parameterization of rainfall microstructure for radar meteorology and hydrology / Remko Uijlenhoet. Doctoral thesis Wageningen University. - With ref. - With summary in Dutch. ISBN 90-5808-156-7 Subject headings: hydrology / meteorology. Abstract Uijlenhoet, R., 1999. Parameterization of rainfall microstructure for radar meteoro­ logy and hydrology. Doctoral thesis, Wageningen University, The Netherlands. 279pp . A comprehensive general framework for the description and analysis of the microstruc­ ture of rainfall is presented. The microstructure of rainfall is parameterized in terms of the raindrop size distribution, which determines both the macroscopic physical properties of rainfall relevant for radar meteorology and hydrology and their relation­ ships. To demonstrate that the definitions of rainfall related variables naturally lead to power law relationships, a rainfall parameterization based on the exponential rain­ drop size distribution is presented. The importance of the distinction between the properties of raindrops present in a volume of air and those of raindrops arriving at a surface is emphasized. A general formulation for the raindrop size distribution as a scaling law is derived, based on the ubiquitous power law relationships between rainfall related variables. The scaling law formulation is independent of any a priori assumption regarding the functional form of the raindrop size distribution and unifies all previously published parameterizations. It allows a separation of the effects of changes in the shape of the raindrop size distribution from those of changes in the rain rate. The values of the scaling exponents indicate whether it is the raindrop concentration or the character­ istic raindrop size which controls the variability of the raindrop size distribution. The gap between the scaling law and traditional parameterizations is bridged by providing explicit expressions for the scaling law for all analytical distributions proposed in the literature. The scaling law formulation is verified experimentally using mean raindrop size distributions for various climatic settings (based on two classical parameterizations) and raw raindrop size distributions from The Netherlands. For the mean distributions the scaling procedure yields excellent results, for the raw distributions a residual amount of scatter about the mean curves remains, indicating that rain rate alone cannot explain all observed variability. As an example of the application of the scaling law, a new method for establishing power law radar reflectivity-rain rate relationships is derived. The method is applied to the mentioned mean and raw distributions. The large inter-event variability of the coefficients indicates that climatological radar reflectivity-rain rate relationships will be of little practical use. The Poisson homogeneity hypothesis, a fundamental assumption in radar meteoro­ logy, is tested on an extraordinary stationary time series of raindrop size distributions. The arrival rate fluctuations of the raindrops which contribute most to rain rate and radar reflectivity are found to behave according to Poisson statistics. Finally, perspectives for future research are presented. Additional index words: raindrop size distribution, scaling law, remote sensing, radar meteorology, hydrology. Voorwoord Hoewel universitaire bestuurders en politici daar nog wel eens anders over willen denken, valt wetenschappelijk onderzoek in het algemeen lastig te plannen. In dat verband is het illustratief de titel van een proefschrift eens met de titel van het oorspronkelijke onderzoeksvoorstel te vergelijken. In mijn geval luidde dat laatste: 'Toepassing van verschillende typen weerradar voor het schatten van neerslag over een verstedelijkt gebied ten behoeve van het waterbeheer'. Het zal duidelijk zijn dat dit proefschrift een enigszins afwijkend onderwerp behandelt. De aandacht is verschoven van de toepassing naar aspecten van de achterliggende theorie. Hetgeen overigens niet wegneemt dat de motivatie voor dit werk altijd de hydrologische toepassing is gebleven. Dat is ook de reden geweest waarom de EU dit onderzoek het afgelopen decennium heeft willen financieren. Uit experimenten uitgevoerd gedurende de eerste jaren van het project bleek echter dat we niet in staat waren om bevredigende ver­ klaringen te vinden voor de discrepanties tussen wat weerradars waarnemen en wat de traditionele regenmeters meten. Daarom is de nadruk van het onderzoek in de loop der jaren meer komen te liggen op het beter begrijpen van de manier waarop de verschillende instrumenten regen meten en daarmee samenhangend het beter be­ grijpen van de structuur van regen zelf. Dit proefschrift behandelt enkele recente ontwikkelingen op dit laatste gebied. Met deze nieuwe inzichten kunnen we nu terug naar de radarmetingen om een poging te wagen de radarhydrologie vlot te trekken. De eerste die ik op deze plaats moet bedanken is mijn directe begeleider, Han Stricker. Hij heeft het onderzoek naar de hydrologische toepassing van weerradar in Wageningen eind jaren tachtig een krachtige impuls gegeven door samenwerking met de radardeskundigen van de Technische Universiteit Delft te zoeken. De regen die voor telecommunicatieonderzoekers 'ruis' is, is voor hydrologen immers 'signaal'. Deze gezamenlijke interesse heeft de basis gelegd voor mijn promotieonderzoek en dit proefschrift is hiervan het uiteindelijke resultaat. Han heeft de inhoudelijke keuzes die ik de afgelopen jaren heb gemaakt altijd gesteund, ook toen het accent van het onderzoek verschoof van toegepast naar meer theoretisch. Hij omschreef dit proces eens als 'van de regen in de drup'. Aannemende dat hij dit in de letterlijke zin van het woord bedoelde, kan de essentie van dit proefschrift inderdaad niet kernachtiger worden omschreven. Herman Russchenberg is vanaf het begin actief bij het onderzoek betrokken ge­ weest. Mede door zijn toedoen is de 'signaal/ruis verhouding' van het Delftse radaron- derzoek de laatste jaren aanzienlijk toegenomen. Regen en wolken zijn van alleen storende factoren een zelfstandig object van studie geworden aan het IRCTR. Dat is de samenwerking met Wageningse en andere onderzoekers vanzelfsprekend alleen maar ten goede gekomen. De interesse van Herman voor mijn werk gedurende de afsluitende fase van het onderzoek heb ik als zeer motiverend ervaren. Mijn promotoren, Prof. Feddes en Prof. Ligthart, bedank ik voor het in mij gestelde vertrouwen. Hoewel ik vrees beiden meer dan eens tot wanhoop gedreven te hebben, zowel door de duur van het onderzoek op zich als door de stortvloed aan leeswerk in de laatste fase, hoop ik dat dit proefschrift toch het begin kan vormen van een hernieuwde Wagenings-Delftse samenwerking op het gebied van de radar remote sensing
Load more

Recommended publications
  • Comparing Historical and Modern Methods of Sea Surface Temperature
    EGU Journal Logos (RGB) Open Access Open Access Open Access Advances in Annales Nonlinear Processes Geosciences Geophysicae in Geophysics Open Access Open Access Natural Hazards Natural Hazards and Earth System and Earth System Sciences Sciences Discussions Open Access Open Access Atmospheric Atmospheric Chemistry Chemistry and Physics and Physics Discussions Open Access Open Access Atmospheric Atmospheric Measurement Measurement Techniques Techniques Discussions Open Access Open Access Biogeosciences Biogeosciences Discussions Open Access Open Access Climate Climate of the Past of the Past Discussions Open Access Open Access Earth System Earth System Dynamics Dynamics Discussions Open Access Geoscientific Geoscientific Open Access Instrumentation Instrumentation Methods and Methods and Data Systems Data Systems Discussions Open Access Open Access Geoscientific Geoscientific Model Development Model Development Discussions Open Access Open Access Hydrology and Hydrology and Earth System Earth System Sciences Sciences Discussions Open Access Ocean Sci., 9, 683–694, 2013 Open Access www.ocean-sci.net/9/683/2013/ Ocean Science doi:10.5194/os-9-683-2013 Ocean Science Discussions © Author(s) 2013. CC Attribution 3.0 License. Open Access Open Access Solid Earth Solid Earth Discussions Comparing historical and modern methods of sea surface Open Access Open Access The Cryosphere The Cryosphere temperature measurement – Part 1: Review of methods, Discussions field comparisons and dataset adjustments J. B. R. Matthews School of Earth and Ocean Sciences, University of Victoria, Victoria, BC, Canada Correspondence to: J. B. R. Matthews ([email protected]) Received: 3 August 2012 – Published in Ocean Sci. Discuss.: 20 September 2012 Revised: 31 May 2013 – Accepted: 12 June 2013 – Published: 30 July 2013 Abstract. Sea surface temperature (SST) has been obtained 1 Introduction from a variety of different platforms, instruments and depths over the past 150 yr.
    [Show full text]
  • ESSENTIALS of METEOROLOGY (7Th Ed.) GLOSSARY
    ESSENTIALS OF METEOROLOGY (7th ed.) GLOSSARY Chapter 1 Aerosols Tiny suspended solid particles (dust, smoke, etc.) or liquid droplets that enter the atmosphere from either natural or human (anthropogenic) sources, such as the burning of fossil fuels. Sulfur-containing fossil fuels, such as coal, produce sulfate aerosols. Air density The ratio of the mass of a substance to the volume occupied by it. Air density is usually expressed as g/cm3 or kg/m3. Also See Density. Air pressure The pressure exerted by the mass of air above a given point, usually expressed in millibars (mb), inches of (atmospheric mercury (Hg) or in hectopascals (hPa). pressure) Atmosphere The envelope of gases that surround a planet and are held to it by the planet's gravitational attraction. The earth's atmosphere is mainly nitrogen and oxygen. Carbon dioxide (CO2) A colorless, odorless gas whose concentration is about 0.039 percent (390 ppm) in a volume of air near sea level. It is a selective absorber of infrared radiation and, consequently, it is important in the earth's atmospheric greenhouse effect. Solid CO2 is called dry ice. Climate The accumulation of daily and seasonal weather events over a long period of time. Front The transition zone between two distinct air masses. Hurricane A tropical cyclone having winds in excess of 64 knots (74 mi/hr). Ionosphere An electrified region of the upper atmosphere where fairly large concentrations of ions and free electrons exist. Lapse rate The rate at which an atmospheric variable (usually temperature) decreases with height. (See Environmental lapse rate.) Mesosphere The atmospheric layer between the stratosphere and the thermosphere.
    [Show full text]
  • Investigating the Climate System Precipitationprecipitation “The Irrational Inquirer”
    Educational Product Educators Grades 5–8 Investigating the Climate System PrecipitationPrecipitation “The Irrational Inquirer” PROBLEM-BASED CLASSROOM MODULES Responding to National Education Standards in: English Language Arts ◆ Geography ◆ Mathematics Science ◆ Social Studies Investigating the Climate System PrecipitationPrecipitation “The Irrational Inquirer” Authored by: CONTENTS Mary Cerullo, Resources in Science Education, South Portland, Maine Grade Levels; Time Required; Objectives; Disciplines Encompassed; Key Terms; Key Concepts . 2 Prepared by: Stacey Rudolph, Senior Science Prerequisite Knowledge . 3 Education Specialist, Institute for Global Environmental Strategies Additional Prerequisite Knowledge and Facts . 5 (IGES), Arlington, Virginia Suggested Reading/Resources . 5 John Theon, Former Program Scientist for NASA TRMM Part 1: How are rainfall rates measured? . 6 Editorial Assistance, Dan Stillman, Truth Revealed after 200 Years of Secrecy! Science Communications Specialist, Pre-Activity; Activity One; Activity Two; Institute for Global Environmental Activity Three; Extensions. 8 Strategies (IGES), Arlington, Virginia Graphic Design by: Part 2: How is the intensity and distribution Susie Duckworth Graphic Design & of rainfall determined? . 9 Illustration, Falls Church, Virginia Airplane Pilot or Movie Critic? Funded by: Activity One; Activity Two. 9 NASA TRMM Grant #NAG5-9641 Part 3: How can you study rain? . 10 Give us your feedback: Foreseeing the Future of Satellites! To provide feedback on the modules Activity One; Activity Two . 10 online, go to: Activity Three; Extensions . 11 https://ehb2.gsfc.nasa.gov/edcats/ educational_product Unit Extensions . 11 and click on “Investigating the Climate System.” Appendix A: Bibliography/Resources . 12 Appendix B: Assessment Rubrics & Answer Keys. 13 NOTE: This module was developed as part of the series “Investigating the Climate Appendix C: National Education Standards.
    [Show full text]
  • Thor's Legions American Meteorological Society Historical Monograph Series the History of Meteorology: to 1800, by H
    Thor's Legions American Meteorological Society Historical Monograph Series The History of Meteorology: to 1800, by H. Howard Frisinger (1977/1983) The Thermal Theory of Cyclones: A History of Meteorological Thought in the Nineteenth Century, by Gisela Kutzbach (1979) The History of American Weather (four volumes), by David M. Ludlum Early American Hurricanes - 1492-1870 (1963) Early American Tornadoes - 1586-1870 (1970) Early American Winters I - 1604-1820 (1966) Early American Winters II - 1821-1870 (1967) The Atmosphere - A Challenge: The Science of Jule Gregory Charney, edited by Richard S. Lindzen, Edward N. Lorenz, and George W Platzman (1990) Thor's Legions: Weather Support to the u.s. Air Force and Army - 1937-1987, by John F. Fuller (1990) Thor's Legions Weather Support to the U.S. Air Force and Army 1937-1987 John F. Fuller American Meteorological Society 45 Beacon Street Boston, Massachusetts 02108-3693 The views expressed in this book are those of the author and do not reflect the official policy or position of the Department of Defense or the United States Government. © Copyright 1990 by the American Meteorological Society. Permission to use figures, tables, and briefexcerpts from this monograph in scientific and educational works is hereby granted provided the source is acknowledged. All rights reserved. No part ofthis publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, elec­ tronic, mechanical, photocopying, recording, or otherwise, without the prior written permis­ sion ofthe publisher. ISBN 978-0-933876-88-0 ISBN 978-1-935704-14-0 (eBook) DOI 10.1007/978-1-935704-14-0 Softcover reprint of the hardcover 1st edition 1990 Library of Congress catalog card number 90-81187 Published by the American Meteorological Society, 45 Beacon Street, Boston, Massachusetts 02108-3693 Richard E.
    [Show full text]
  • 5-6 Meteorology Notes
    What is meteorology? A. METEOROLOGY: an atmospheric science that studies the day to day changes in the atmosphere 1. ATMOSPHERE: the envelope of gas that surrounds the surface of Earth; the air 2. WEATHER: the day to day changes in the atmosphere caused by shifts in temperature, air pressure, and humidity B. Meteorologists are scientists that study atmospheric sciences that include the following: 1. CLIMATOLOGY: the study of climate 2. ATMOSPHERIC CHEMISTRY: the study of chemicals in the air 3. ATMOSPHERIC PHYSICS: the study of how air behaves 4. HYRDOMETEOROLOGY: the study of how oceans interact with weather What is the atmosphere? A. The earth’s atmosphere is made of air. 1. Air is a mixture of matter that includes the following: a. 78% nitrogen gas b. 21% oxygen gas c. 0.04% carbon dioxide d. 0.96% other components like water vapor, dust, smoke, salt, methane, etc. 2. The atmosphere goes from the Earth’s surface to 700km up. 3. The atmosphere is divided into 4 main layers as one ascends. What is the atmosphere? a. TROPOSPHERE: contains most air, where most weather occurs, starts at sea level b. STRATOSPHERE: contains the ozone layer that holds back some UV radiation c. MESOSPHERE: slows and burns up meteoroids d. THERMOSPHERE: absorbs some energy from the sun What is the atmosphere? B. The concentration of air in the atmosphere increases the closer one gets to sea level. 1. The planet’s gravity pulls the atmosphere against the surface. 2. Air above pushes down on air below, causing a higher concentration in the troposphere.
    [Show full text]
  • HISTORY of WEATHER OBSERVATIONS Fort Snelling, Minnesota 1819 - 1892
    HISTORY OF WEATHER OBSERVATIONS Fort Snelling, Minnesota 1819 - 1892 December 2005 Prepared by: Gary K. Grice Information Manufacturing Corporation Rocket Center, West Virginia Peter Boulay Minnesota State Climatology Office DNR-Waters St. Paul, Minnesota This report was prepared for the Midwestern Regional Climate Center under the auspices of the Climate Database Modernization Program, NOAA’ National Climatic Data Center, Asheville, North Carolina TABLE OF CONTENTS Acknowledgments ii LIST OF ILLUSTRATIONS iii INTRODUCTION Historical Overview 1 Goal of the Study 3 LOCATION OF OBSERVATIONS 4 INSTRUMENTATION Parameters Measured/Observed 8 Instrument Type and Exposure 15 OTHER OBSERVATIONS 25 BIBLIOGRAPHY 26 APPENDIX Methodology 28 i Acknowledgments Previous research by Charles Fisk (Master’s Thesis) and by Tom St. Martin (self-published) was very helpful in developing a time line for this report. Their hard work and excellent research are greatly appreciated. The authors also appreciate the expert advice and assistance provided by the staff of the Minnesota Historical Society. Text, photographs, and particularly staff insights, were invaluable in answering specific questions relevant to Fort Snelling. ii LIST OF ILLUSTRATIONS Figures 1. Fort Snelling and Surrounding Area 1 2. Location of Fort Snelling 2 3. Topographical Map of Fort Snelling 4 4. Photograph of Fort Snelling (1860s) 5 5. Schematic of Reconstructed Fort Snelling 7 6. Drawing of the Interior of Fort Snelling (1853) 7 7. Observation Form for St. Peter (1820) 8 8. Observation Form for Fort Snelling (1836) 10 9. Observation Form for Fort Snelling (1841) 11 10A&B. Observation Forms for Fort Snelling (1843) 13 11. Observation Form for Fort Snelling (1888) 15 12.
    [Show full text]
  • Lecture 7A: Cloud Development and Forms
    Lecture 7a: Cloud Development and Forms (from “The Blue Planet”) Why Clouds Form Cloud Types ESS55 Prof. Jin-Yi Yu Why Clouds Form? Clouds form when air rises and becomes saturated in response to adiabatic cooling. ESS55 Prof. Jin-Yi Yu Four Ways to Lift Air Upward (1) Localized Convection cold front (2) Convergence (4) Frontal Lifting Lifting warm front (3) Orographic Lifting ESS55 (from “The Blue Planet”) Prof. Jin-Yi Yu Orographic Lifting ESS55 Prof. Jin-Yi Yu Frontal Lifting When boundaries between air of unlike temperatures (fronts) migrate, warmer air is pushed aloft. This results in adiabatic cooling and cloud formation. Cold fronts occur when warm air is displaced by cooler air. Warm fronts occur when warm air rises over and displaces cold air. ESS55 Prof. Jin-Yi Yu Cloud Type Based On Properties Four basic cloud categories: Cirrus --- thin, wispy cloud of ice. Stratus --- layered cloud Cumulus --- clouds having vertical development. Nimbus --- rain-producing cloud These basic cloud types can be combined to generate ten different cloud types, such as cirrostratus clouds that have the characteristics of cirrus clouds and stratus clouds. ESS55 Prof. Jin-Yi Yu Cloud Types ESS55 Prof. Jin-Yi Yu Cloud Types Based On Height If based on cloud base height, the ten principal cloud types can then grouped into four cloud types: High clouds -- cirrus, cirrostratus, cirroscumulus. Middle clouds – altostratus and altocumulus Low clouds – stratus, stratocumulus, and nimbostartus Clouds with extensive vertical development – cumulus and cumulonimbus. (from “The Blue Planet”) ESS55 Prof. Jin-Yi Yu Cloud Classifications (from “The Blue Planet”) ESS55 Prof.
    [Show full text]
  • Some Basic Elements of Thunderstorm Forecasting
    (] NOAA TECHNICAL MEMORANDUM NWS CR-69 SOME BASIC ELEMENTS OF THUNDERSTORM FORECASTING Richard P. McNulty National Weather Service Forecast Office Topeka, Kansas May 1983 UNITED STATES I Nalion•l Oceanic and I National Weather DEPARTMENT OF COMMERCE Almospheric Adminislralion Service Malcolm Baldrige. Secretary John V. Byrne, Adm1mstrator Richard E. Hallgren. Director SOME BASIC ELEMENTS OF THUNDERSTORM FORECASTING 1. INTRODUCTION () Convective weather phenomena occupy a very important part of a Weather Service office's forecast and warning responsibilities. Severe thunderstorms require a critical response in the form of watches and warnings. (A severe thunderstorm by National Weather Service definition is one that produces wind gusts of 50 knots or greater, hail of 3/4 inch diameter or larger, and/or tornadoes.) Nevertheless, heavy thunderstorms, those just below severe in­ ·tensity or those producing copious rainfall, also require a certain degree of response in the form of statements and often staffing. (These include thunder­ storms producing hail of any size and/or wind gusts of 35 knots or greater, or storms producing sufficiently intense rainfall to possess a potential for flash flooding.) It must be realized that heavy thunderstorms can have as much or more impact on the public, and require as much action by a forecast office, as do severe thunderstorms. For the purpose of this paper the term "signi­ ficant convection" will refer to a combination of these two thunderstorm classes. · It is the premise of this paper that significant convection, whether heavy or severe, develops from similar atmospheric situations. For effective opera­ tions, forecasters at Weather Service offices should be familiar with those factors which produce significant convection.
    [Show full text]
  • Tropical Cyclones: Meteorological Aspects Mark A
    Tropical Cyclones: Meteorological Aspects Mark A. Lander1 Water and Environmental Research Institute of the Western Pacific, University of Guam, UOG Station, Mangilao, Guam (USA) 96923 Sailors have long recognized the existence of deadly storms in Every year, TCs claim many lives—occasionally exceeding tropical latitudes where the weather was usually a mix of bright sun and 100,000. Some of the world’s greatest natural disasters have been gentle breezes with quickly passing showers. These terrifying storms associated with TCs. For example, Tropical Cyclone 02B was the were known to have a core of screaming winds accompanied by deadliest and most destructive natural disaster on earth in 1991. The blinding rain, spume and sea spray, and sharply lowered barometric associated extreme storm surge along the coast of Bangladesh was the pressure. When the sailors were lucky enough to survive penetration primary reason for the loss of 138,000 lives (Joint Typhoon Warning to the core of such violent weather, they found a region of calm. This Center, 1991). It occurred 19 years after the loss of ≈300,000 lives in region is the signature characteristic and best-known feature of these Bangladesh by a similar TC striking the low-lying Ganges River storms—the eye (Fig. 1). region in April 1970. In a more recent example, flooding caused by These violent storms of the tropical latitudes were known to be Hurricane Mitch killed 10,000+ people in Central America in Fall seasonal, hence their designation by Atlantic sailors as “line” storms, 1998. Nearly all tropical islands—the islands of the Caribbean, Ha- in reference to the sun’s crossing of the line (equator) in September (the waii, French Polynesia, Micronesia, Fiji, Samoa, Mauritius, La Re- month of peak hurricane activity in the North Atlantic).
    [Show full text]
  • Meteorology (METEO) 1
    Meteorology (METEO) 1 METEOROLOGY (METEO) METEO 4: Weather and Risk 3 Credits METEO 2: Our Changing Atmosphere: Personal and Societal Non-technical introduction to the science and historical development Consequences of meteorology, and the role of weather forecasting as a tool for risk 3 Credits management by individuals, businesses, and societies. METEO 4 traces the development of weather forecasting as both a scientific discipline A survey of meteorology emphasizing how the nature of our lives, and as a tool for risk management. Beginning from the pre-modern individually/societally, depends upon atmospheric structure, quality, history of weather forecasting as a diverse set of folkloric and ritualistic and processes. METEO 002 Our Changing Atmosphere: Personal and practices, the emergence of meteorology as a genuine science has Societal Consequences (3) (GN)(BA) This course meets the Bachelor enabled the development of powerful tools for managing risks faced of Arts degree requirements. The primary objective is to provide the by individuals, businesses and societies.Students will learn about the student with an understanding of the mechanisms that determine fundamental principles that govern the global atmospheric circulation, local and regional weather and climate patterns, with emphasis on how and how this circulation shapes weather and climate. They will learn these factors impact individuals and society. We focus on the energy how this scientific understanding has served as the foundation of a balance of the atmosphere and the forces that drive motion and that are global system of weather observation and forecasting, encompassing ultimately responsible for surface properties such as precipitation and a worldwide network of atmospheric observing instruments, powerful air quality.
    [Show full text]
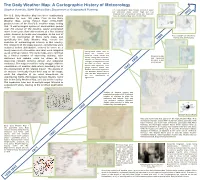
  • The Daily Weather Map: a Cartographic History of Meteorology
    The Daily Weather Map: A Cartographic History of Meteorology Stephen Vermette, SUNY Buffalo State, Department of Geography & Planning U.S. Daily Weather Map remains a sheet of paper but additional maps added: High and Low Temperatures; Precipitation Areas and Amounts; The U.S. Daily Weather Map has been continuously 1:30 p.m. Weather Map; and 700 mb Chart. published for over 140 years. Prior to the Daily Weather Map, James Pollard Espy (1785–1860) produced one of the first U.S. weather maps, noting that “A well-arranged system of observations spread over the course of the country, would accomplish more in one year, than observations at a few isolated posts, however accurate and complete, to the end of First available on Internet for time”. An examination of these early maps, and viewing and downloading. specifically the Daily Weather Map, reveals the evolution of meteorological science in this country. The relevance of the maps evolved – initially they were outdated before distribution, evolved to serve as a timely source of information, and later were relegated Precipitation areas Last 24 as an archival record. The early maps were confined hours) are shaded. Low by a limited number of observing stations, later pressure storm tracks are Reduced in size isotherms and isobars could be drawn as the shown. Along with isotherms, and expanded dashed red isolines indicate observing network became denser and expanded to cover a one changes in temperature over week period. westward. The maps reveal the early struggle with the the past 24 hours. Tabular visualization of weather data which eventually led to station data expanded, river gauge stations added, and the development of the ‘station model’.
    [Show full text]
  • Tropical Cyclone Energetics and Structure
    Tropical Cyclone Energetics and Structure Kerry Emanuel Program in Atmospheres, Oceans, and Climate Massachusetts Institute of Technology 1. Introduction Aircraft measurements of tropical cyclones that commenced during World War II allowed scientists of that era to paint the first reasonably detailed picture of the wind and thermal structure of tropical cyclones. This led to the first attempts to quantify the energy cycle of these storms and to understand the physical control of their structure. In this contribution, I review the history of research on the energy cycle and structure of tropical cyclones and offer a revised interpretation of their structure. 2. Energetics The first reasonably accurate description of the energy cycle of tropical cyclones appeared in a paper by Herbert Riehl (1950). To the best of this author’s knowledge, this is the first paper in which it is explicitly recognized that the energy source of hurricanes arises from the in situ evaporation of ocean water1. By the next year, another German scientist, Ernst Kleinschmidt, could take it for granted that “the heat removed from the sea by the storm is the basic energy source of the typhoon” (Kleinschmidt, 1951). Kleinschmidt also showed that thermal wind balance in a hurricane-like vortex, coupled with assumed moist adiabatic lapse rates on angular momentum surfaces, implies a particular shape of such surfaces. He assumed that a specified fraction, q , of the azimuthal velocity that would obtain if angular momentum were conserved in the inflow, is left by the time the air reaches the eyewall, and derived an expression for the maximum wind speed: q2 vE2 = 2 (1) max 1− q2 where E is the potential energy found from a tephigram, assuming that air ascending in the eyewall has acquired some additional enthalpy from the ocean.
    [Show full text]