DOCSLIB.ORG

Recursive Descent Parser

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Recursive Descent Parser MIT 6. 035 Top-Down Parsing Martin Rinard Laboratory for Computer Science Massachusetts Institute of Technology Orientation • Language specification • Lexical structure – regular expressions • Syntactic structure – grammar • This Lecture - recursive ddescentescent parsers • Code parser as set of mutually recursive procedures • Structure ooff pprogramrogram matches sstructuretructure of grammar Starting Point • Assume lexical analysis has produced a sequence of tokens • Each token has a type and value • Types ccorrespondorrespond ttoo tterminalserminals • Values to contents of token read in • Examples • Int 549 – integer token with value 549 read in • if - if keyword, no need for a value • AddOp + - add operator, value + Basic Approach • Start with Start symbol • Bu ild a le ftft most der iva tion • If leftmost symbol is nonterminal, choose a production and applyapply itit • If leftmost symbol is terminal, match against input • If all terminals match, have found a parse! •Key: find correct productions for nonterminals Graphical Illustration of Leftmost Derivation Sentential Form NT1 T1 T2 T3 NT2 NT3 Apply Production Not Here Here Grammar for Parsing Example Start → Expr • Set ooff ttokokensens iiss Expr → Expr + Term { +, -, *, /, Int }, where Expr → Expr - Term Int = [0-9][0-9]* Expr → Term • FFoo r ccononveeniencenience , may reprepreesentsent Term → Term * Int each Int n token by n Term → Term / Int Term → Int Parsing Example Parse Remaining Input Tree Start 2-2*2 Sentential Form Start Current Position in Parse Tree Parsing Example Parse Remaining Input Tree Start 2-2*2 Exprp Sentential Form Expr Apppplied Production Start → Expr Current Position in Parse Tree Parsing Example Parse Remaining Input Tree Start 2-2*2 Exprp Sentential Form Expr - Term Expr - Term Expr → Expr + Term Apppplied Production Expr → Expr - Term Expr → Term Expr → Expr - Term Parsing Example Parse Remaining Input Tree Start 2-2*2 Exppr Sentential Form Expr - Term Term - Term Term Exprp → Exprp + Teerm Apppplied Production Expr → Expr - Term Expr → Term Expr →→Te Termrm Parsing Example Parse Remaining Input Tree Start 2-2*2 Exppr Sentential Form Expr - Term Int - Term Term Apppplied Production Int Term → Int Parsing Example Parse Remaining Input Tree Start Match Input 2-2*2 Exppr Token! Sentential Form Expr - Term 2 - Term Term Int 2 Parsing Example Parse Remaining Input Tree Start Match Input -2*2 Exppr Token! Sentential Form Expr - Term 2 - Term Term Int 2 Parsing Example Parse Remaining Input Tree Start Match Input 2*2 Exppr Token! Sentential Form Expr - Term 2 - Term Term Int 2 Parsing Example Parse Remaining Input Tree Start 2*2 Exppr Sentential Form Expr - Term 2 - Term *Int Term Term * Int Apppplied Production Int 2 Term → Term * Int Parsing Example Parse Remaining Input Tree Start 2*2 Exppr Sentential Form Expr - Term 2 - Int * Int Term Term * Int Apppplied Production Int 2 Int Term → Int Parsing Example Parse Remaining Input Tree Start Match Input 2*2 Exppr Token! Sentential Form Expr - Term 2 - 2* Int Term Term * Int Int 2 Int 2 Parsing Example Parse Remaining Input Tree Start Match Input *2 Exppr Token! Sentential Form Expr - Term 2 - 2* Int Term Term * Int Int 2 Int 2 Parsing Example Parse Remaining Input Tree Start Match Input 2 Exppr Token! Sentential Form Expr - Term 2 - 2* Int Term Term * Int Int 2 Int 2 Parsing Example Parse Remaining Input Tree Start Parse Complete! 2 Exppr Sentential Form Expr - Term 2 - 2* 2 Term Term * Int 2 Int 2 Int 2 Summary • Three Actions (Mechanisms) • AlApply pro ductit ion to expand current nonterminal in parse tree • Match ccurrenturrent terminal (consuming input) • Accept the parse as correct • Parser generates ppreorderreorder ttraversalraversal of parse ttreeree • visit parents before children • visit ssiblingsiblings ffromrom llefteft ttoo rrightight Policy Problem • Which production to use for each nonterminal? • Classical Separation of Policy and Mechanism • One Approach: Backtracking • Treat it as a search problem • At each choice point, try next alternative • If it is clear that current try fails, go back to previous choice and trytry something ddifferentifferent • General technique for searching • Used a lot in classical AI and natural langgguage processing (parsing, speech recognition) Backtracking Example Parse Remaining Input Tree Start 2-2*2 Sentential Form Start Backtracking Example Parse Remaining Input Tree Start 2-2*2 Exp r Sentential Form Expr Applied Production Start → Expr Backtracking Example Parse Remaining Input Tree Start 2-2*2 Expr Sentential Form Expr + Term Expr + Term Applied Production Expr → Expr + Term Backtracking Example Parse Remaining Input Tree Start 2-2*2 Expr Sentential Form Expr + Term Term + Term Term Applied Production Expr → Term Backtracking Example Parse Remaining Input Tree Start Match Input 2-2*2 Expr Token! Sentential Form Expr + Term Int + Term Term Applied Production Int Term → Int Backtracking Example Parse Remaining Input Tree Start Can’ t Match -2*2 Expr Input Sentential Form Token! Expr + Term 2 - Term Term Applied Production Int 2 Term → Int Backtracking Example Parse Remaining Input Tree Start So Backtrack! 2-2*2 Exp r Sentential Form Expr Applied Production Start → Expr Backtracking Example Parse Remaining Input Tree Start 2-2*2 Expr Sentential Form Expr - Term Expr - Term Applied Production Expr → Expr - Term Backtracking Example Parse Remaining Input Tree Start 2-2*2 Expr Sentential Form Expr - Term Term - Term Term Applied Production Expr → Term Backtracking Example Parse Remaining Input Tree Start 2-2*2 Expr Sentential Form Expr - Term Int - Term Term Applied Production Int Term → Int Backtracking Example Parse Remaining Input Tree Start Match Input -2*2 Expr Token! Sentential Form Expr - Term 2 - Term Term Int 2 Backtracking Example Parse Remaining Input Tree Start Match Input 2*2 Expr Token! Sentential Form Expr - Term 2 - Term Term Int 2 Left Recursion + Top-Down Parsing = Infinite Loop • Example Production: Term → Term*Num • PtPoten ttiial pars ing steps: Term Term Term Num Term * Num Term * Term * Num General Search Issues • Three components • Search space (parse trees) • Search algorithm (parsing(parsing algorithm)algorithm) • Goal to find (parse tree for input program) • Would like to (but can’t always) ensure that • Find goal (hopefully quickly) if it exists • Search terminates if it does not • Handled inin variousvarious ways in various contextscontexts • Finite search space makes it easy • Exploration strategies for infinite search space • Sometimes oneone goal more important (model checking) • For parsing, hack grammar to remove left recursion Eliminating Left Recursion • Start with productions of form •A→ A α • A →β • α, β sequences of terminals and nonterminals that do not startstart with A • Repeated application of A →A α A builds parseparse tree like tthis:his: A α A α β α Eliminating Left Recursion • Replacement productions –A→ A α A →βR R is a new nonterminal –A→β R →αR – R → ε New ParseParse TTrreeee Old Parse Tree A A R β R A α α R β α α ε Hacked Grammar Original Grammar New Grammar Fragment Fragment Te rm → In t Te rm ’ Term → Term * Int Term’ → * Int Term’ Term → Term / Int Term’ → / Int Term’ Term → Int Term’ → ε Parse Tree Comparisons Original Grammar New GGrraammarmmar Term Term Int Term’ Term * Int Term’ Int * Int * Int * Int Term’ ε Eliminating Left Recursion • Changes search space exploration algorithm • EElilim ina tes didirec t iifnfiiinitte recursion • But grammar less intuitive • Sets things up for predictivepredictive pparsingarsing Predictive Parsing • Alternative to backtracking • UfUseful for programming lan guages, whihich can be designed to make parsing easier • Basic iideadea • Look ahead in input stream • Decide which pproductionroduction ttoo aapplypply bbasedased on next tokens in input stream • We will use one token of lookahead Predictive Parsing Example Grammar Start → Expr Te rm → In t Te rm ’ Expr → Term Expr’ Term’ → * In t Term’ Expr’ → + Expr’ Term’ → / In t Term’ Expr’ → - Expr’ Term’ → ε Expr’ → ε Choice Points • Assume Term’ is current position in parse tree • Have three possiblepossible productionsproductions to apply Term’ → * Int Term’ Teerm’ → / Int Teerm’ Term’ →ε • Use next token to decide • If next token is *, apply Term’ → * Int Term’ • If next token is /, apply Term’ → / Int Term’ • Otherwise , aapplypply Term ’ → ε Predictive Parsing + Hand Coding = Recursive DescentDescent Parser • One procedure per nonterminal NT • PdProducttiions NT → β1 , …, NT → βn • Procedure examines the current input symbol T to determine which production to apppply •If T∈First(βk) • Apply production k • Consume terminals in βk (h(check for correct terminal) • Recursively call procedures for nonterminals in βk • Current input symbol stored in global variable token • Procedures return • true if parse succeedssucceeds • false if parse fails Boolean Term() Example if (token = Int n) token = NextToken(); return(TermPrime()) else return(false) Boolean TTermPrime()ermPrime() if (token = *) token = NextToken(); if (token = Int n) token = NexttTToken(); return((TTermPrime()) else return(false) else if (token = /) token = NextToken(); if (token = Int n) token = NextToken(); return(TermPrime()) else return(false) else return(true) Term → Int Term’ Term’ → * Int Term’ Term’ → / Int Term’ Term’ →ε Multiple Productions With Same Prefix in RHS • Example Grammar NT → if then NT → if then else • Assume NT is current position in parse ttree ree, aandnd if is the next token • Unclear whichwhich production to apply • Multiple
Load more

Recommended publications
  • Syntax-Directed Translation, Parse Trees, Abstract Syntax Trees
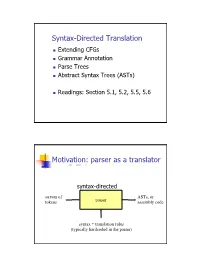
    Syntax-Directed Translation Extending CFGs Grammar Annotation Parse Trees Abstract Syntax Trees (ASTs) Readings: Section 5.1, 5.2, 5.5, 5.6 Motivation: parser as a translator syntax-directed translation stream of ASTs, or tokens parser assembly code syntax + translation rules (typically hardcoded in the parser) 1 Mechanism of syntax-directed translation syntax-directed translation is done by extending the CFG a translation rule is defined for each production given X Æ d A B c the translation of X is defined in terms of translation of nonterminals A, B values of attributes of terminals d, c constants To translate an input string: 1. Build the parse tree. 2. Working bottom-up • Use the translation rules to compute the translation of each nonterminal in the tree Result: the translation of the string is the translation of the parse tree's root nonterminal Why bottom up? a nonterminal's value may depend on the value of the symbols on the right-hand side, so translate a non-terminal node only after children translations are available 2 Example 1: arith expr to its value Syntax-directed translation: the CFG translation rules E Æ E + T E1.trans = E2.trans + T.trans E Æ T E.trans = T.trans T Æ T * F T1.trans = T2.trans * F.trans T Æ F T.trans = F.trans F Æ int F.trans = int.value F Æ ( E ) F.trans = E.trans Example 1 (cont) E (18) Input: 2 * (4 + 5) T (18) T (2) * F (9) F (2) ( E (9) ) int (2) E (4) * T (5) Annotated Parse Tree T (4) F (5) F (4) int (5) int (4) 3 Example 2: Compute type of expr E -> E + E if ((E2.trans == INT) and (E3.trans == INT) then E1.trans = INT else E1.trans = ERROR E -> E and E if ((E2.trans == BOOL) and (E3.trans == BOOL) then E1.trans = BOOL else E1.trans = ERROR E -> E == E if ((E2.trans == E3.trans) and (E2.trans != ERROR)) then E1.trans = BOOL else E1.trans = ERROR E -> true E.trans = BOOL E -> false E.trans = BOOL E -> int E.trans = INT E -> ( E ) E1.trans = E2.trans Example 2 (cont) Input: (2 + 2) == 4 1.
    [Show full text]
  • Derivatives of Parsing Expression Grammars
    Derivatives of Parsing Expression Grammars Aaron Moss Cheriton School of Computer Science University of Waterloo Waterloo, Ontario, Canada [email protected] This paper introduces a new derivative parsing algorithm for recognition of parsing expression gram- mars. Derivative parsing is shown to have a polynomial worst-case time bound, an improvement on the exponential bound of the recursive descent algorithm. This work also introduces asymptotic analysis based on inputs with a constant bound on both grammar nesting depth and number of back- tracking choices; derivative and recursive descent parsing are shown to run in linear time and constant space on this useful class of inputs, with both the theoretical bounds and the reasonability of the in- put class validated empirically. This common-case constant memory usage of derivative parsing is an improvement on the linear space required by the packrat algorithm. 1 Introduction Parsing expression grammars (PEGs) are a parsing formalism introduced by Ford [6]. Any LR(k) lan- guage can be represented as a PEG [7], but there are some non-context-free languages that may also be represented as PEGs (e.g. anbncn [7]). Unlike context-free grammars (CFGs), PEGs are unambiguous, admitting no more than one parse tree for any grammar and input. PEGs are a formalization of recursive descent parsers allowing limited backtracking and infinite lookahead; a string in the language of a PEG can be recognized in exponential time and linear space using a recursive descent algorithm, or linear time and space using the memoized packrat algorithm [6]. PEGs are formally defined and these algo- rithms outlined in Section 3.
    [Show full text]
  • Lecture 4 Dynamic Programming
    1/17 Lecture 4 Dynamic Programming Last update: Jan 19, 2021 References: Algorithms, Jeff Erickson, Chapter 3. Algorithms, Gopal Pandurangan, Chapter 6. Dynamic Programming 2/17 Backtracking is incredible powerful in solving all kinds of hard prob- lems, but it can often be very slow; usually exponential. Example: Fibonacci numbers is defined as recurrence: 0 if n = 0 Fn =8 1 if n = 1 > Fn 1 + Fn 2 otherwise < ¡ ¡ > A direct translation in:to recursive program to compute Fibonacci number is RecFib(n): if n=0 return 0 if n=1 return 1 return RecFib(n-1) + RecFib(n-2) Fibonacci Number 3/17 The recursive program has horrible time complexity. How bad? Let's try to compute. Denote T(n) as the time complexity of computing RecFib(n). Based on the recursion, we have the recurrence: T(n) = T(n 1) + T(n 2) + 1; T(0) = T(1) = 1 ¡ ¡ Solving this recurrence, we get p5 + 1 T(n) = O(n); = 1.618 2 So the RecFib(n) program runs at exponential time complexity. RecFib Recursion Tree 4/17 Intuitively, why RecFib() runs exponentially slow. Problem: redun- dant computation! How about memorize the intermediate computa- tion result to avoid recomputation? Fib: Memoization 5/17 To optimize the performance of RecFib, we can memorize the inter- mediate Fn into some kind of cache, and look it up when we need it again. MemFib(n): if n = 0 n = 1 retujrjn n if F[n] is undefined F[n] MemFib(n-1)+MemFib(n-2) retur n F[n] How much does it improve upon RecFib()? Assuming accessing F[n] takes constant time, then at most n additions will be performed (we never recompute).
    [Show full text]
  • Exhaustive Recursion and Backtracking
    CS106B Handout #19 J Zelenski Feb 1, 2008 Exhaustive recursion and backtracking In some recursive functions, such as binary search or reversing a file, each recursive call makes just one recursive call. The "tree" of calls forms a linear line from the initial call down to the base case. In such cases, the performance of the overall algorithm is dependent on how deep the function stack gets, which is determined by how quickly we progress to the base case. For reverse file, the stack depth is equal to the size of the input file, since we move one closer to the empty file base case at each level. For binary search, it more quickly bottoms out by dividing the remaining input in half at each level of the recursion. Both of these can be done relatively efficiently. Now consider a recursive function such as subsets or permutation that makes not just one recursive call, but several. The tree of function calls has multiple branches at each level, which in turn have further branches, and so on down to the base case. Because of the multiplicative factors being carried down the tree, the number of calls can grow dramatically as the recursion goes deeper. Thus, these exhaustive recursion algorithms have the potential to be very expensive. Often the different recursive calls made at each level represent a decision point, where we have choices such as what letter to choose next or what turn to make when reading a map. Might there be situations where we can save some time by focusing on the most promising options, without committing to exploring them all? In some contexts, we have no choice but to exhaustively examine all possibilities, such as when trying to find some globally optimal result, But what if we are interested in finding any solution, whichever one that works out first? At each decision point, we can choose one of the available options, and sally forth, hoping it works out.
    [Show full text]
  • A Typed, Algebraic Approach to Parsing
    A Typed, Algebraic Approach to Parsing Neelakantan R. Krishnaswami Jeremy Yallop University of Cambridge University of Cambridge United Kingdom United Kingdom [email protected] [email protected] Abstract the subject have remained remarkably stable: context-free In this paper, we recall the definition of the context-free ex- languages are specified in BackusśNaur form, and parsers pressions (or µ-regular expressions), an algebraic presenta- for these specifications are implemented using algorithms tion of the context-free languages. Then, we define a core derived from automata theory. This integration of theory and type system for the context-free expressions which gives a practice has yielded many benefits: we have linear-time algo- compositional criterion for identifying those context-free ex- rithms for parsing unambiguous grammars efficiently [Knuth pressions which can be parsed unambiguously by predictive 1965; Lewis and Stearns 1968] and with excellent error re- algorithms in the style of recursive descent or LL(1). porting for bad input strings [Jeffery 2003]. Next, we show how these typed grammar expressions can However, in languages with good support for higher-order be used to derive a parser combinator library which both functions (such as ML, Haskell, and Scala) it is very popular guarantees linear-time parsing with no backtracking and to use parser combinators [Hutton 1992] instead. These li- single-token lookahead, and which respects the natural de- braries typically build backtracking recursive descent parsers notational semantics of context-free expressions. Finally, we by composing higher-order functions. This allows building show how to exploit the type information to write a staged up parsers with the ordinary abstraction features of the version of this library, which produces dramatic increases programming language (variables, data structures and func- in performance, even outperforming code generated by the tions), which is sufficiently beneficial that these libraries are standard parser generator tool ocamlyacc.
    [Show full text]
  • Backtrack Parsing Context-Free Grammar Context-Free Grammar
    Context-free Grammar Problems with Regular Context-free Grammar Language and Is English a regular language? Bad question! We do not even know what English is! Two eggs and bacon make(s) a big breakfast Backtrack Parsing Can you slide me the salt? He didn't ought to do that But—No! Martin Kay I put the wine you brought in the fridge I put the wine you brought for Sandy in the fridge Should we bring the wine you put in the fridge out Stanford University now? and University of the Saarland You said you thought nobody had the right to claim that they were above the law Martin Kay Context-free Grammar 1 Martin Kay Context-free Grammar 2 Problems with Regular Problems with Regular Language Language You said you thought nobody had the right to claim [You said you thought [nobody had the right [to claim that they were above the law that [they were above the law]]]] Martin Kay Context-free Grammar 3 Martin Kay Context-free Grammar 4 Problems with Regular Context-free Grammar Language Nonterminal symbols ~ grammatical categories Is English mophology a regular language? Bad question! We do not even know what English Terminal Symbols ~ words morphology is! They sell collectables of all sorts Productions ~ (unordered) (rewriting) rules This concerns unredecontaminatability Distinguished Symbol This really is an untiable knot. But—Probably! (Not sure about Swahili, though) Not all that important • Terminals and nonterminals are disjoint • Distinguished symbol Martin Kay Context-free Grammar 5 Martin Kay Context-free Grammar 6 Context-free Grammar Context-free
    [Show full text]
  • Adaptive LL(*) Parsing: the Power of Dynamic Analysis
    Adaptive LL(*) Parsing: The Power of Dynamic Analysis Terence Parr Sam Harwell Kathleen Fisher University of San Francisco University of Texas at Austin Tufts University [email protected] [email protected] kfi[email protected] Abstract PEGs are unambiguous by definition but have a quirk where Despite the advances made by modern parsing strategies such rule A ! a j ab (meaning “A matches either a or ab”) can never as PEG, LL(*), GLR, and GLL, parsing is not a solved prob- match ab since PEGs choose the first alternative that matches lem. Existing approaches suffer from a number of weaknesses, a prefix of the remaining input. Nested backtracking makes de- including difficulties supporting side-effecting embedded ac- bugging PEGs difficult. tions, slow and/or unpredictable performance, and counter- Second, side-effecting programmer-supplied actions (muta- intuitive matching strategies. This paper introduces the ALL(*) tors) like print statements should be avoided in any strategy that parsing strategy that combines the simplicity, efficiency, and continuously speculates (PEG) or supports multiple interpreta- predictability of conventional top-down LL(k) parsers with the tions of the input (GLL and GLR) because such actions may power of a GLR-like mechanism to make parsing decisions. never really take place [17]. (Though DParser [24] supports The critical innovation is to move grammar analysis to parse- “final” actions when the programmer is certain a reduction is time, which lets ALL(*) handle any non-left-recursive context- part of an unambiguous final parse.) Without side effects, ac- free grammar. ALL(*) is O(n4) in theory but consistently per- tions must buffer data for all interpretations in immutable data forms linearly on grammars used in practice, outperforming structures or provide undo actions.
    [Show full text]
  • Parsing 1. Grammars and Parsing 2. Top-Down and Bottom-Up Parsing 3
    Syntax Parsing syntax: from the Greek syntaxis, meaning “setting out together or arrangement.” 1. Grammars and parsing Refers to the way words are arranged together. 2. Top-down and bottom-up parsing Why worry about syntax? 3. Chart parsers • The boy ate the frog. 4. Bottom-up chart parsing • The frog was eaten by the boy. 5. The Earley Algorithm • The frog that the boy ate died. • The boy whom the frog was eaten by died. Slide CS474–1 Slide CS474–2 Grammars and Parsing Need a grammar: a formal specification of the structures allowable in Syntactic Analysis the language. Key ideas: Need a parser: algorithm for assigning syntactic structure to an input • constituency: groups of words may behave as a single unit or phrase sentence. • grammatical relations: refer to the subject, object, indirect Sentence Parse Tree object, etc. Beavis ate the cat. S • subcategorization and dependencies: refer to certain kinds of relations between words and phrases, e.g. want can be followed by an NP VP infinitive, but find and work cannot. NAME V NP All can be modeled by various kinds of grammars that are based on ART N context-free grammars. Beavis ate the cat Slide CS474–3 Slide CS474–4 CFG example CFG’s are also called phrase-structure grammars. CFG’s Equivalent to Backus-Naur Form (BNF). A context free grammar consists of: 1. S → NP VP 5. NAME → Beavis 1. a set of non-terminal symbols N 2. VP → V NP 6. V → ate 2. a set of terminal symbols Σ (disjoint from N) 3.
    [Show full text]
  • Abstract Syntax Trees & Top-Down Parsing
    Abstract Syntax Trees & Top-Down Parsing Review of Parsing • Given a language L(G), a parser consumes a sequence of tokens s and produces a parse tree • Issues: – How do we recognize that s ∈ L(G) ? – A parse tree of s describes how s ∈ L(G) – Ambiguity: more than one parse tree (possible interpretation) for some string s – Error: no parse tree for some string s – How do we construct the parse tree? Compiler Design 1 (2011) 2 Abstract Syntax Trees • So far, a parser traces the derivation of a sequence of tokens • The rest of the compiler needs a structural representation of the program • Abstract syntax trees – Like parse trees but ignore some details – Abbreviated as AST Compiler Design 1 (2011) 3 Abstract Syntax Trees (Cont.) • Consider the grammar E → int | ( E ) | E + E • And the string 5 + (2 + 3) • After lexical analysis (a list of tokens) int5 ‘+’ ‘(‘ int2 ‘+’ int3 ‘)’ • During parsing we build a parse tree … Compiler Design 1 (2011) 4 Example of Parse Tree E • Traces the operation of the parser E + E • Captures the nesting structure • But too much info int5 ( E ) – Parentheses – Single-successor nodes + E E int 2 int3 Compiler Design 1 (2011) 5 Example of Abstract Syntax Tree PLUS PLUS 5 2 3 • Also captures the nesting structure • But abstracts from the concrete syntax a more compact and easier to use • An important data structure in a compiler Compiler Design 1 (2011) 6 Semantic Actions • This is what we’ll use to construct ASTs • Each grammar symbol may have attributes – An attribute is a property of a programming language construct
    [Show full text]
  • Backtracking / Branch-And-Bound
    Backtracking / Branch-and-Bound Optimisation problems are problems that have several valid solutions; the challenge is to find an optimal solution. How optimal is defined, depends on the particular problem. Examples of optimisation problems are: Traveling Salesman Problem (TSP). We are given a set of n cities, with the distances between all cities. A traveling salesman, who is currently staying in one of the cities, wants to visit all other cities and then return to his starting point, and he is wondering how to do this. Any tour of all cities would be a valid solution to his problem, but our traveling salesman does not want to waste time: he wants to find a tour that visits all cities and has the smallest possible length of all such tours. So in this case, optimal means: having the smallest possible length. 1-Dimensional Clustering. We are given a sorted list x1; : : : ; xn of n numbers, and an integer k between 1 and n. The problem is to divide the numbers into k subsets of consecutive numbers (clusters) in the best possible way. A valid solution is now a division into k clusters, and an optimal solution is one that has the nicest clusters. We will define this problem more precisely later. Set Partition. We are given a set V of n objects, each having a certain cost, and we want to divide these objects among two people in the fairest possible way. In other words, we are looking for a subdivision of V into two subsets V1 and V2 such that X X cost(v) − cost(v) v2V1 v2V2 is as small as possible.
    [Show full text]
  • Sequence Alignment/Map Format Specification
    Sequence Alignment/Map Format Specification The SAM/BAM Format Specification Working Group 3 Jun 2021 The master version of this document can be found at https://github.com/samtools/hts-specs. This printing is version 53752fa from that repository, last modified on the date shown above. 1 The SAM Format Specification SAM stands for Sequence Alignment/Map format. It is a TAB-delimited text format consisting of a header section, which is optional, and an alignment section. If present, the header must be prior to the alignments. Header lines start with `@', while alignment lines do not. Each alignment line has 11 mandatory fields for essential alignment information such as mapping position, and variable number of optional fields for flexible or aligner specific information. This specification is for version 1.6 of the SAM and BAM formats. Each SAM and BAMfilemay optionally specify the version being used via the @HD VN tag. For full version history see Appendix B. Unless explicitly specified elsewhere, all fields are encoded using 7-bit US-ASCII 1 in using the POSIX / C locale. Regular expressions listed use the POSIX / IEEE Std 1003.1 extended syntax. 1.1 An example Suppose we have the following alignment with bases in lowercase clipped from the alignment. Read r001/1 and r001/2 constitute a read pair; r003 is a chimeric read; r004 represents a split alignment. Coor 12345678901234 5678901234567890123456789012345 ref AGCATGTTAGATAA**GATAGCTGTGCTAGTAGGCAGTCAGCGCCAT +r001/1 TTAGATAAAGGATA*CTG +r002 aaaAGATAA*GGATA +r003 gcctaAGCTAA +r004 ATAGCT..............TCAGC -r003 ttagctTAGGC -r001/2 CAGCGGCAT The corresponding SAM format is:2 1Charset ANSI X3.4-1968 as defined in RFC1345.
    [Show full text]
  • Lexing and Parsing with ANTLR4
    Lab 2 Lexing and Parsing with ANTLR4 Objective • Understand the software architecture of ANTLR4. • Be able to write simple grammars and correct grammar issues in ANTLR4. EXERCISE #1 Lab preparation Ï In the cap-labs directory: git pull will provide you all the necessary files for this lab in TP02. You also have to install ANTLR4. 2.1 User install for ANTLR4 and ANTLR4 Python runtime User installation steps: mkdir ~/lib cd ~/lib wget http://www.antlr.org/download/antlr-4.7-complete.jar pip3 install antlr4-python3-runtime --user Then in your .bashrc: export CLASSPATH=".:$HOME/lib/antlr-4.7-complete.jar:$CLASSPATH" export ANTLR4="java -jar $HOME/lib/antlr-4.7-complete.jar" alias antlr4="java -jar $HOME/lib/antlr-4.7-complete.jar" alias grun='java org.antlr.v4.gui.TestRig' Then source your .bashrc: source ~/.bashrc 2.2 Structure of a .g4 file and compilation Links to a bit of ANTLR4 syntax : • Lexical rules (extended regular expressions): https://github.com/antlr/antlr4/blob/4.7/doc/ lexer-rules.md • Parser rules (grammars) https://github.com/antlr/antlr4/blob/4.7/doc/parser-rules.md The compilation of a given .g4 (for the PYTHON back-end) is done by the following command line: java -jar ~/lib/antlr-4.7-complete.jar -Dlanguage=Python3 filename.g4 or if you modified your .bashrc properly: antlr4 -Dlanguage=Python3 filename.g4 2.3 Simple examples with ANTLR4 EXERCISE #2 Demo files Ï Work your way through the five examples in the directory demo_files: Aurore Alcolei, Laure Gonnord, Valentin Lorentz. 1/4 ENS de Lyon, Département Informatique, M1 CAP Lab #2 – Automne 2017 ex1 with ANTLR4 + Java : A very simple lexical analysis1 for simple arithmetic expressions of the form x+3.
    [Show full text]