Stroke-Based Handwriting Recognition: Theory and Applications
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Trace Resourcebook: Assistive Technologies for Communication, Control and Computer Access, 1993-94 Edition
DOCUMENT RESUME ED 363 079 EC 302 545 AUTHOR Borden, Peter A.; And Others TITLE Trace ResourceBook: Assistive Technologies for Communication, Control and Computer Access, 1993-94 Edition. INSTITUTION RESNA: Association for the Advancement of Rehabilitation Technology, Washington, DC.; Wisconsin Univ., Madison. Trace Center. SPONS AGENCY National Inst. on Disability and Rehabilitation Researc:11 (ED/OSERS), Washington, DC. REPORT NO ISBN-0-945459-03-3 PUB DATE 93 NOTE 964p. AVAILABLE FROM Trace Research and Development Center, S-151 Waisman Center, University of Wisconsin-Madison, 1500 Highland Ave., Madison, WI 53705 ($40). PUB TYPE Reference Materials Directories/Catalogs (132) EDRS PRICE MF07/PC39 Plus Postage. DESCRIPTORS Accessibility (for Disabled); *Assistive Devices (for Disabled); *Communication Aids (for Disabled); Computers; Computer Software; *Disabilities; Electronic Equipment; Input Output Devices; Microcomputers; *Rehabilitation; *Technology ABSTRACT This volume lists and describes products pertaining to assistive and rehabilitative technologies in the areas of communication, control, and computer access, as well as special software. Part 1, covering communication for individuals with disabilities, includes products designed as aids to both electronic and nonelectronic communication. It includes aids that supplement speech or replace speech, as well as products that help with the process of nonspeech communication. Part 2, covering the area of control, includes special switches plus environmental controls and calling devices. Part 3 lists products which provide disabled people with access to computers, such as keyboard modifications, alternate inputs, input adapters, alternate display systems, braille printers, and speech synthesizers. Part 4 describes special software written specifically for the needs of people with disabilities and professionals who work with them, addressing the areas of administration and management, assessment, education and training, recreation, and personal tools. -

Lucrare De Disertaţie
Universitatea POLITEHNICA din Bucureşti Facultatea INGINERIA şi MANAGEMENTUL SISTEMULUI TEHNOLOGIC Centrul PREMINV Cursul postuniversitar Informatică Aplicată LUCRARE DE DISERTAŢIE TABLETA GRAFICĂ Coordonator : S.L. univ. dr. ing. Ghinea Mihalache Student : Stîngă (Buzatu) Cristina Bucureşti, 2012 Universitatea Politehnica Bucuresti Lucrare de dizertaţie Facultatea IMST Stîngă (Buzatu) Cristina Centru PREMINV Universitatea POLITEHNICA din Bucureşti Facultatea INGINERIA şi MANAGEMENTUL SISTEMULUI TEHNOLOGIC Centrul PREMINV Cursul postuniversitar Informatică Aplicată PARTEA I TABLETA GRAFICĂ 2 Tableta grafică http://grupafetesti-upb.yolasite.com Universitatea Politehnica Bucuresti Lucrare de dizertaţie Facultatea IMST Stîngă (Buzatu) Cristina Centru PREMINV CUPRINS CUPRINS .............................................................................................................................................. 3 INTRODUCERE .................................................................................................................................. 4 CAP 1. UTILIZAREA TEHNOLOGIEI TOUCHSCREEN ................................................................ 6 1.1 Principiul de funcţionare ..................................................................................................... 6 1.2. Tipuri de ecrane touchscreen .................................................................................................. 7 1.3 Principii de funcţionarea a ecranelor rezistive şi a celor capacitive .................................. 12 -

SIGGRAPH 1987: Art Show
FOURTEENTH ANNUAL CONFERENCE ON COMPUTER GRAPHICS AND INTERACTIVE TECHNIQUES A N A H E M, C A L.I F O R N JULY 27-31, July 27-31, 1987 Co-Chairs: . Anaheim, California James J. Thomas Robert J. Young ART SHOW COMMlffEE SPECIAL ACKNOWLEDGEMENTS Joanne P. Culver The SIGGRAPH '87 Art Show would like to especially thank the Art Show Chair following: Crimson Indigo American Lasers, Corp., Salt Lake City, UT Administrative Assistant Anthro, Portland, OR Jeffrey Murray Apple Computer, CA Holography Institute Coherent Lasers, Inc., Palo Alto, CA Danzing Lazars, San Francisco, CA Larry Shaw Exploratorium D.C. Productions, Oakland, CA Dot-Dash, Oakland, CA Gay Graves DUNN Instruments, Inc., Springfield, VA NASA Helix Productions, Alameda, .CA Laurin Herr Holography Institute, Petaluma, CA Pacific Interface IBM The Lasersmith, Inc., Chicago, IL Louise Ledeen G.E.S.I. LAZERUS, Berkeley, CA NO-Coast Design, DeKalb, IL Frank Dietrich Schier Associates, Oakland, CA University of Utah Tektronix, Beaverton, OR TerryDowd Raytel, Troy, NY Terry Dowd, Inc. Zeta Music Systems, Berkeley, CA Darcy Gerbarg Sanity Maintenance provided by the music of: Bryan Ferry, School of Visual Arts Roxy Music, Mike Oldfield, Alyson Moyet, Vangelis, & Yanni. Patric Prince California State University Barbara Mones-Hattal Montgomery College THE SIGGRAPH LOGO HOLOGRAM The image affixed to the cover of this catalog is an original computer-generated holographic image created by developing a unique three-dimensional database model designed for holographic dynamics. The model is based on the original two-dimensional conference logo. Lighting, movement and three-dimensional dynamics were effected in the computer model. -

Washington Apple Pi Journal, November 1987
$ 250 Walhington Apple Pi The Journal of Washingtond Apple Pi, Ltd. Volume. 9 november1987 number II Hiahliahtl • Beginner's Start at the IIGS Finder • I Love Apple Music: Pa-rt 6 • Disk III Backup (g Laser Printing &Mac Typesetting ~ A View of Big Blue [!g) You're Going to Love These! (Suitcase, PowerStation, Pyr~) In TI,is Issue... Officers & Staff, Editorial ....................... .... .......... ....... 3 Spy's Adventures in Europe: A Review ...... Chris Hancock 36 President's Comer ..................................... Tom Warrick 4 Battles in Normandy: A Review ............... Chris Hancock 36 General Information ........................ ............................ 5 The Fool's Errand: A Review ..................... Steven Payne 37 Classifieds, Commercial Classifieds, Job Mart .................. 6 Software Industry: Econ. Struct. Part 2 ... Joseph A. Hasson 39 WAP Hotline ......................................................... ..... 8 Pascal News ................................. ........ Robert C. Platt 48 WAP Calendar, SIG News............................................ 9 dPub SIG Meeting Report-Oct 7 ........... Cynthia Yockey 50 Stripping Your GS System Disk ................... David Todd 10 Laser Printing and Mac Typesetting .......... Lynn R. Trusal 52 IIGS SIG Meeting Report .............................. Ted Meyer 10 Stock SIG News ............... ........... Andrew D. Thompson 55 Beginner's Guide at the IIGS Finder ................. Ted Meyer 12 Mac Meeting Report-Sept. 26 .............. Cynthia Yockey 56 Minutes ........................................ -

Advanced Certification in Science - Level I
Advanced Certification in Science - Level I www.casiglobal.us | www.casi-india.com | CASI New York; The Global Certification body. Page 1 of 391 CASI New York; Reference material for ‘Advanced Certification in Science – Level 1’ Recommended for college students (material designed for students in India) About CASI Global CASI New York CASI Global is the apex body dedicated to promoting the knowledge & cause of CSR & Sustainability. We work on this agenda through certifications, regional chapters, corporate chapters, student chapters, research and alliances. CASI is basically from New York and now has a presence across 52 countries. World Class Certifications CASI is usually referred to as one of the BIG FOUR in education, CASI is also referred to as the global certification body CASI offers world class certifications across multiple subjects and caters to a vast audience across primary school to management school to CXO level students. Many universities & colleges offer CASI programs as credit based programs. CASI also offers joint / cobranded certifications in alliances with various institutes and universities. www.casiglobal.us CASI India CASI India has alliances with hundreds of institutes in India where students of these institutes are eligible to enroll for world class certifications offered by CASI. The reach through such alliances is over 2 million citizens CASI India also offers cobranded programs with Government Polytechnic and many other institutes of higher learning. CASI India has multiple franchises across India to promote certifications especially for school students. www.casi-india.com Volunteering @ CASI NY CASI India / CSR Diary also provide volunteering opportunities and organizes mega format events where in citizens at large can also volunteer for various causes. -
Mini'app'les Apple Computer User Group Newsletter
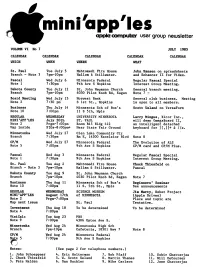
mini'app'les apple computer user group newsletter VOLUME VI No 7 JULY 1983 CALENDAR CALENDAR CALENDAR CALENDAR CALENDAR WHICH WHEN WHERE WHAT St. Paul Tue July 5 Mahtomedi Fire House John Hansen on spreadsheets Branch - Note 3 7pm-10pm Hallam & Stillwater. and Enhancer II for Videx. Pascal Wed July 6 Minnesota Federal Regular Pascal Special Note 1 7:30pm 9th Ave S Hopkins Interest Group Meeting. Dakota County Tue July 12 St. John Neumann Church General branch meeting. Branch 7pm-10pm 4030 Pilot Knob Rd, Eagan Note 7 - Board Meeting Wed July 13 Norwest Bank General club business. Meeting Note 2 7:30 pm S 1st St., Hopkins is open to all members. Business Thu July 14 Minnesota Sch of Bus's Scott Ueland on VersaForra Note 10 7:00pm 11 S 5th, Mpls REGULAR WEDNESDAY UNIVERSITY MINNESOTA Larry Mingus, Xicor Inc., MINI1 APPLES July 20th ST. PAUL will demo OmegaBoard II, Note 2 Prgm-7:00pm Room B45 Bldg 412 an intelligent detached Map inside SIGs-8:00pm+ Near State Fair Ground keyboard for ][,][+ & lie. Minnetonka Wed July 27 Glen Lake Community Ctr Branch 7:30pm Rm E, 14300 Excelsior Blvd Note 8 CP/M Wed July 27 Minnesota Federal The Evolution of ALS Note 5 7:00pm 9th Ave S Hopkins CP/M card and CP/M Plus. Pascal Wed Aug 3 Minnesota Federal Regular Pascal Special Note 1 7:30pm 9th Ave S Hopkins Interest Group Meeting. St. Paul Tue Aug 2 Mahtomedi Fire House Chuck Thiesfeld on Branch - Note 3 7pm-10pm Hallam & Stillwater. Pascal Dakota County Tue Aug 9 St. -

Computer Applications in Reading. Third Edition. INSTITUTION International Reading Association, Newark,Del
DOCUMENTRESUME ED 285 136 CS 008 903 AUTHOR Blanchard, Jay S.; And Others TITLE Computer Applications in Reading. Third Edition. INSTITUTION International Reading Association, Newark,Del. REPORT NO ISBN-0-87207-785-3 PUB DATE 87 NOTE 208p.; For previous editions,see ED 173 771 and ED 249 483. AVAILABLE FROM International Reading Association, 800Barksdale Rd., PO Box 8139, Newark, DE 19714-8139 (Book No. 785, $7.00 member, $10.50 nonmember). PUB TYPE Books (010) -- Guides - Non-ClassroomUse (055) EDRS PRICE M701/PC09 Plus Postage. DESCRIPTORS American Indian Education; Artificial Intelligence; Authoring Aids (Programing); Cloze Procedure; Communications Satellites; Computer Assisted Instruction; Computer Assisted Testing; *Computer Managed Instruction; Computer Software; *Computer Software Reviews; *Computer Uses in Education; Elementary Secondary Education; English (Second Language); Higher Education; LanguageArts; Language Experience Approach; Optical Disks;Program Development; Programing Languages; *Reading Instruction; Reading Programs; Reading Research; Reading Writing Relationship; Special Education; Spelling; *Technological Advancement; Teleconferencing; Word Processing; Writing Instruction IDENTIFIERS LOGO Programing Language ABSTRACT Intended as a reference for researchers,teachers, and administrators, this book chroniclesresearch, programs, and uses of computers in reading. Chapter 1 providesa broad view of computer applications in education, while Chapter 2 providesannotated references for computer based reading and languagearts -

Compute Sep 1988
CLASSIC SOFTWARE! 70 ALL-TIME BEST september 1988 COMPUTE! 7i'elef: 1alt}1!/ o;, I IOTl-I YEAR CONNECTYOURCOMPUTER1bA HIGHER INTELLIGENCE. CompuServe's reference straight to the reference information income, and occupation in any U.S. databases make you more you need in seconds. community. For a geography report, productive, competitive, Access thousands of sources of a business plan, or a family move. and better informed. information in the areas of business, All you need to access CompuServe's finance, medicine, education, unlimited world of information is a Remember the last time you tried to demographics, science, law, news, modem and just about any personal get your hands on hard-to-find facts? In popular entertainment, and sports. computer. Visit your computer dealer a magazine article you read a year ago. today. To order direct, or for more In a news report you never saw. Or in a What you know can help you. information, call or write: table of data you didn't know existed. Research an industry or company Imagine those facts just a few through articles, financial statements, keystrokes away on your personal and other sources. Analyze an C:OntpuServe® computer. Through CompuServe. investment. Assist in a job search. lnlormalion Services, P.O. Box 20212 Follow market competition. Investigate 5000 Ar1ing1on Cenlre Blvd.. Columbus. OH 43220 Your personal research center. a business opportunity. SOo-848-8199 In Ohio and Canada. call 614 457-0802 Save hours of research by going Check characteristics such as age, AA H&R BIOc:k Company WINNER! Best Educational Program With Designasaurus from Survive as a Brontosaurus, Print out 12 different dinosaurs. -
Washington Apple Pi Journal, February 1987
$ 250 Wa/hiftgtOft Apple Pi The Journal of Washington8 Apple Pi, Ltd . Volum<Z.9 FebruarllJ 1987 number 2 Hi~lhliahtl- - • Introduction to dBase lI .jl:\~:;: ~ ~ ;.:~)~~:~ : :s~· : • Family Home Money Ma 'n ' ager:~ Part 9 • ~ Views and Reviews: 12 Computer Magazines (g MacNovice: Easy 1st Project With Excel ~ Excel Graphics: Scatter Plots, Trend Functions In This Issue.. Officers & Staff, Editorial ................ ................ .. ............ 3 Best of Apple Items from TCS ............. Euclid Coukouma 34 President's Comer ................................ ...... Tom Warrick 4 Stock SIG News ......................... Andrew D. Thompson 37 Classifieds, Commercial Classifieds ................................. 6 Music SIG News ........................ .. .. ..... Raymond Hobbs 37 Job Mart, Event Queue .... .. .......................................... .. 6 View From the Hill: BASIC .. .. ........ .. ........ Rich Norling 38 WAP Calendar, SigNews ......................... .. .. .................. 7 Pascal News .............. .......................... Robert C. Platt 40 WAP Hotline .............................................. .............. .. 8 Future of Amer. Business:A Book Rev ... Joseph A. Hasson 42 ByLaws Changes, General Information ..................... ........ 9 Views and Reviews ........ .. ................. .. Raymond Hobbs 44 On the Trail of the Apple III ..................... David Ottalini 10 dPub SIG News ....................................... Steven Payne 46 Q & A ......................... Bruce F. Field & Robert -

Commodore Revue Magazine (French) Issue 11
M 2483 -11- 28,00 F GRAPHISME : SCULP-TANIMATE 4D AMIGA NEWS TECH : LES PRINCIPES DE L'AMIGADOS : LE 3792483028004 00110 REPORTAGE CEBIT DE HANOVRE ICO^MODORE 6" S //* ë V É I EDITO iCOMÉMODORE Comme convenu dans notre dernier numéro, vous N° 11 découvrirez dans Commodore Revue de ce mois-ci, plus AVRIL 1989 de deux pages consacrées au previews jeux. Mais là ne s'arrêtent pas les nouveautés, puisque nous vous avons concocté un véritable cahier technique, bourré de recet- tes diverses pour mieux utiliser votre Amiga. De ce fait, la pagination augmente pour atteindre les 92 pages, ce qui ne sera pas pour vous déplaire, j'en suis persuadé. Un fastueux dossier de neuf pages attend les passion- nés de la 3D en page 26, réalisé par un maître en la matière : Frédéric Louguet, Mips pour les intimes. MUSIQUI Encore un petit mot avant que vous ne partiez à la décou- AUDIOMASTER, verte de cette mine d'informations : Commodore Revue sera présent au Sicob à partir du 17 avril sur un stand attenant celui de Commodore France. Venez nous voir SCULPT nombreux, une surprise vous y attend. En effet, nous pré- ANIMATE 4D L'imaae de synthèse prend parons à cette occasion un « Guide de l' Amiga, logiciels une nouvelle dimension. d'application et hardware », de plus de 250 pages au for- mat livre (15x21). Pour en savoir plus référez-vous à HARDWARE la page 86. En ce qui concerne le service minitel « Com SCANNER PRINT TECHNIK Rev », cela se précise, il devrait, si tout se passe bien, être ouvert à tous pour le premier Avril {non, non, ce n'est pas une farce...). -

Apple 2 Computer Family Technical Information
APPLE 2 COMPUTER FAMILY TECHNICAL INFORMATION APPLE 2 COMPUTER ————————————————————— Hardware Info comp.sys.apple2(CSA2)Usenet newsgroup Apple II FAQs 28 May 1999 Apple 2 Computer Info -- Apple 2 Hardware Info -- comp.sys.apple2 -- 28 May 1999 -- 1 of 452 APPLE 2 COMPUTER FAMILY TECHNICAL INFORMATION ##################################################################### ### FILE: a2.hw ##################################################################### Path: news.weeg.uiowa.edu!news.uiowa.edu!hobbes.physics.uiowa.edu!moe.ksu.ksu.edu!ux1.cs o.uiuc.edu!newsrelay.iastate.edu!iscsvax.uni.edu!thompsa1597 From: [email protected] Newsgroups: comp.sys.apple2 Subject: Re: Language Card access -- do $C08x switches work on IIGS? Message-ID: <[email protected]> Date: 7 Jun 93 00:43:28 -0600 References: <[email protected]> Organization: University of Northern Iowa Lines: 225 FIre up your copy buffers. This should answer your question about the soft switches. Four pages of goodies no Appler should be without: SOFT SWITCHES +--------+---------------+---------+---------+-----+ | ACTION | ADDRESS | READ | WRITE? | $D0 | +--------+---------------+---------+---------+-----+ | R | $C080 / 49280 | RAM | NO | 2 | | RR | $C081 / 49281 | ROM | YES | 2 | |de R | $C082 / 49282 | ROM | NO | 2 | | RR | $C083 / 49283 | RAM | YES | 2 | | R | $C088 / 49288 | RAM | NO | 1 | | RR | $C089 / 49289 | ROM | YES | 1 | | R | $C08A / 49290 | ROM | NO | 1 | | RR | $C08B / 49291 | RAM | YES | 1 | +--------+---------------+---------+---------+-----+ |de W | $C008 / 49160 | MAIN ZPAGE,STACK,LC | | W | $C009 / 49161 | AUX. ZPAGE,STACK,LC | +--------+---------------+-------------------------+ | R7 | $C011 / 49169 | $D0 BANK 2(1) OR 1(0) | | R7 | $C012 / 49170 | READ RAM(1) OR ROM(0) | | R7 | $C016 / 49174 | USE AUX(1) OR MAIN(0) | +--------+---------------+-------------------------+ |de W | $C002 / 49154 | READ FROM MAIN 48K | | W | $C003 / 49155 | READ FROM AUX. -

Diplomová Práce
UNIVERZITA PALACKÉHO V OLOMOUCI PEDAGOGICKÁ FAKULTA Ústav pedagogiky a sociálních studií Diplomová práce Bc. Helena Koutná Využití grafického tabletu ve výuce na středních odborných školách Olomouc 2019 Vedoucí práce: PhDr. René Szotkowski, Ph.D. Prohlášení Prohlašuji, že jsem svou diplomovou práci na téma „Využití grafického tabletu ve výuce na středních odborných školách“ vypracovala samostatně a použil jen uvedených pramenů a literatury pod vedením pana PhDr. René Szotkowski, Ph.D. V Olomouci dne 20. 11. 2019 ………………………………… Bc. Helena Koutná Poděkování Děkuji PhDr. Renému Szotkowskému, Ph.D. za odborné vedení a cenné připomínky při zpracování mé diplomové práce a RNDr. Ing. Martinu Radvanskému, M.Sc., Ph.D. za odborný dohled při zpracování statistických dat. Obsah Úvod .................................................................................................................................. 6 I TEORETICKÁ ČÁST 1 Grafický tablet v systému didaktických prostředků ............................................... 9 1.1 Didaktické prostředky ........................................................................................... 9 1.2 Rozdělení didaktických prostředků ....................................................................... 9 1.3 Nemateriální didaktické prostředky .................................................................... 10 1.3.1 Výuková metoda ........................................................................................... 10 1.3.2 Didaktické zásady ........................................................................................