DOCSLIB.ORG

Bioinformatical Analysis of Intrinsically Disordered Regions in Eukaryotes: Insights Into the Evolution of Folding-On-Binding

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Bioinformatical Analysis of Intrinsically Disordered Regions in Eukaryotes: Insights Into the Evolution of Folding-On-Binding ! ! ! ! ! !"#"$%#&'()"*(+,($(+-.".,#%,"$)&"$."*(++-,/".#&/0&0/,&01"#$.,"$, 023(&-#)0.4,5$."16).,"$)#,)60,07#+2)"#$,#%,%#+/"$18#$89"$/"$1, &01"#$.,($/,:#.)8)&($.+()"#$(+,'#/"%"*()"#$., ! ! "#$%&%'%()$*+!,%-%).*%&+! ! ! /01%-2*0&2!#3!4+#'#56! "78+''!9&+:0-)+26! "#&2-0%';!<.0=07;!>%&%?%! ! @ABCD!EFGH! ! ! ! @!2$0)+)!).=*+220?!2#!"78+''!9&+:0-)+26!+&!1%-2+%'!3.'3+'*0&2!#3!2$0!-0I.+-0*0&2)!#3!2$0! ?05-00!#3!/#72#-!#3!A$+'#)#1$6!+&!4+#'#56!J4+#+&3#-*%2+7)!7#&70&2-%2+#&K! ! L!EFGH!"#$%&%'%()$*+!,%-%).*%&+! ! ! ! ! ! ! ! ! ! ;!<=>;?=, ! C&2-+&)+7%''6!?+)#-?0-0?!1-#20+&)!JC/A)K!#-!C&2-+&)+7%''6!?+)#-?0-0?!-05+#&)!JC/B)K!+&! 1-#20+&)!7%&!0M$+=+2!%!1%-2+%''6!3#'?0?!#-!.&3#'?0?!)2%20!.&?0-!1$6)+#'#5+7%'!7#&?+2+#&)!=.2! 7#&30-!)0:0-%'!3.&72+#&%'!%?:%&2%50)N!C/B)!7%&!3#'?!+&2#!%!)2%='0!20-2+%-6!)2-.72.-0!O$0&! =#.&?!2#!2$0+-!1%-2&0-!*#'07.'0;!%!2-%&)+2+#&!2$%2!7%&!=0!1-#*#20?!=6!1#)2P2-%&)'%2+#&%'! *#?+3+7%2+#&)!JAQ")KN!C&2-+&)+7!?+)#-?0-!+)!3#.&?!+&!%''!?#*%+&)!#3!'+30!=.2!+)!1-0:%'0&2!+&! 0.(%-6#20)N! Q$+)! 2$0)+)! +&:0)2+5%20)! 2$0! 7#*1#)+2+#&! %&?! 0:#'.2+#&%-6! =0$%:+#.-! #3! ?+)#-?0-0?!-05+#&)!2$%2!.&?0-5#!?+)#-?0-P2#P#-?0-!2-%&)+2+#&!%&?!2$0!0:#'.2+#&%-6!2-0&?!#3! AQ")!+&!C/B)!%7-#))!0.(%-6#20)!.)+&5!7#*1.2%2+#&%'!*02$#?)!%&?!2##')N!! ! 4+#+&3#-*%2+7%'!1%-)+&5!#3!$.*%&!3#'?+&5P#&P=+&?+&5!JR4K!1-#20+&)!+&2#!3#.-!).=)02)! J#-?0-0?;!R4);!?+)#-?0-0?!-05+#&)!2$%2!).--#.&?!R4);!%&?!#2$0-!?+)#-?0-0?!-05+#&)K!O%)! 10-3#-*0?! 2#! 0M%*+&0! O$02$0-! 2$0! 7#*1#)+2+#&! %&?! 0:#'.2+#&%-6! =0$%:+#.-! J%7-#))! :0-20=-%20! #-2$#'#5)K! %-0! ?+330-0&2! +&! 2$0)0! 3#.-! ).=)02)N! Q$+)! %&%'6)+)! -0:0%'0?! 2$%2! 7#*1#)+2+#&%''6;!#-?0-0?!1-#20+&!-05+#&)!%-0!?+)2+&72!3-#*!2$0!2$-00!#2$0-!).=)02);!=.2!2$0! R4! -05+#&)! %-0! #3! 7#*1%-%='0! 0:#'.2+#&%-6! 7#&)0-:%2+#&! 2#! 2$0! #-?0-0?! -05+#&)N! /+)#-?0-0?! -05+#&)! ).--#.&?+&5! R4! -05+#&)! %-0! *#-0! &05%2+:0'6! 7$%-50?! %&?! '0))! 7#&)0-:0?! 2$%&! 2$0+-! %?S%70&2! R4! -05+#&)N! Q$0! 1-0)0&20?! -0).'2)! ).550)2! 2$0! -#'0! #3! $6?-#1$+'+7!#-!7$%-50?!-0)+?.0)!%-#.&?!R4)!+&!)200-+&5!R4!-05+#&)!2#O%-?)!2$0!=+&?+&5! )+20)!#3!1%-2&0-!*#'07.'0)N!Q$0!+&)+5$2)!5%+&0?!3-#*!%&%'6)+)!#3!0:#'.2+#&%-6!7#&)0-:%2+#&! 3#-! R4)! 1-#:+?0?! *#2+:%2+#&! 2#! 0M%*+&0! %! -0'%20?! I.0)2+#&;! &%*0'6! 2$0! 0:#'.2+#&%-6! 7#&)0-:%2+#&!#3!AQ")!+&!C/A)TC/B);!+&!7#*1%-+)#&!2#!AQ")!+&!#-?0-0?!-05+#&)N!! ! +! ! ! ! ! ! C&! %&#2$0-! =+#+&3#-*%2+7%'! %11-#%7$;! 2$0! 7#&)0-:%2+#&! %&?! 0*0-50&70! #3! *02$6'%2+#&;!%7026'%2+#&!%&?!.=+I.+2+&%2+#&!)+20)!+&!#-?0-0?!%&?!?+)#-?0-0?!-05+#&)!O0-0! 0M%*+&0?!%7-#))!GG!0:#'.2+#&%-6!7'%?0)!?#O&!3-#*!2$0!O$#'0!0.(%-6#2+7!?#*%+&!2#!2$0! %10! ).10-3%*+'6N! Q$0)0! )+20)! #77.-! *%+&'6! %2! %-5+&+&0! %&?! '6)+&0! -0)+?.0)N! C2! O%)! ?+)7#:0-0?!2$%2!"@9!AQ"!+)!%!*%S#-!?-+:0-!#3!7#&)0-:%2+#&!3#-!%-5+&+&0)!%&?!'6)+&0)!+&! =#2$!#-?0-0?!%&?!?+)#-?0-0?!-05+#&);!%7-#))!2$0!GG!'0:0');!*#)2!)+5&+3+7%&2'6!%7-#))!2$0! *%**%'+%&! 7'%?0N! R.-2$0-*#-0;! 2$0! 0*0-50&70! #3! %! )+5&+3+7%&2! &.*=0-! #3! &0O! '6)+&0! "@9!)+20)!+)!3#.&?!+&!2$0!?+)#-?0-0?!-05+#&)!#3!1-#20+&)!+&!?0.20-#)2#*0)!%&?!*%**%')N! C&!$+)2#&0);!"@9!)+20)!0M$+=+2!%!?+)2+&72!)+5&+3+7%&2!7#&)0-:%2+#&!1%220-&!0:+?0&2!%)!3%-! =%7(!%)!2$0!'%)2!7#**#&!%&70)2#-!#3!*%**%')N!C&!%!)01%-%20!*.'2+1'0!0:#'.2+#&%-6!'0:0'! %&%'6)+)! #3! 2$0! 0M10-+*0&2%''6P:0-+3+0?! $.*%&! R4! -05+#&);! %! )+5&+3+7%&2! 0&-+7$*0&2! #3! 7#&)0-:0?!.=+I.+2+&%2+#&!)+20)!+&!R4!-05+#&)!O%)!+?0&2+3+0?!%2!%''!0:#'.2+#&%-6!'0:0')!=%7(! %)!3%-!%)!*%**%')N!U+*+'%-'6;!R4!-05+#&)!)$#O0?!%!)+5&+3+7%&2!1-030-0&70!3#-!)+20)!O+2$! *.'2+1'0!"@9!*#?+3+7%2+#&)!O$0&!2-0%20?!=#2$!%)!%!)%*1'0!#3!#-?0-0?!%&?!#3!?+)#-?0-0?! -05+#&)N!Q$0)0!-0).'2)!+&?+7%20!2$0!&00?!2#!7#&)+?0-!)0I.0&70!%&%'6)+)!#3!C/B)!%2!*.'2+1'0! 0:#'.2+#&%-6! '0:0')! +&! #-?0-! 2#! .&?0-)2%&?! 2$0+-! 7#*1'0M! 0:#'.2+#&%-6! 1%220-&)N! Q$0! 1-0)0&20?!)2.?6!%)!%!O$#'0!?0*#&)2-%20)!2$0!?+)2+&72+:0!%*+&#!%7+?!7#*1#)+2+#&;!AQ"! 1-030-0&70! %&?! 7#&)0-:%2+#&! #3! C/B)! 2$%2! 0M$+=+2! ?+330-0&2! 7#&3#-*%2+#&%'! )2%20)! J0N5N! ?+)#-?0-0?;! ?+)#-?0-0?! %-#.&?! R4! %&?! R4! -05+#&)K;! %&?! 2$0! +&20-1'%6! =02O00&! 2$0)0! 1-#10-2+0)N! ! ! ++! ! ! ! ! >@<AB@, D0)! 1-#2V+&0)! +&2-+&)WI.0*0&2! ?V)#-?#&&V0)! JC/A)K! #.! '0)! -V5+#&)! +&2-+&)WI.0*0&2! ?V)#-?#&&V0)! JC/B)K! ?%&)! '0)! 1-#2V+&0)! 10.:0&2! *#&2-0-! .&! V2%2! 1%-2+0''0*0&2! -01'+V! #.! &#&P-01'+V! ?%&)! ?0)! 7#&?+2+#&)! 1$6)+#'#5+I.0)! *%+)! 7#&3W-0&2! 1'.)+0.-)!%:%&2%50)!3#&72+#&&0')N!D0)!C/B)!10.:0&2!)0!-01'+0-!0&!.&0!)2-.72.-0!20-2+%+-0! )2%='0!I.%&?!0''0)!)0!'+0&2!X!'0.-!*#'V7.'0!%))#7+V0;!.&0!2-%&)+2+#&!I.+!10.2!Y2-0!3%7+'+2V! 1%-!?0)!*#?+3+7%2+#&)!1#)2P2-%?.72+#&!JAQ")KN!D0!?V)#-?-0!+&2-+&)WI.0!)0!-0&7#&2-0!?%&)! 2#.)! '0)! ?#*%+&0)! ?.! :+:%&2! *%+)! 0)2! 2-W)! 3-VI.0&2! 7$0Z! '0)! 0.7%-6#20)N! >0220! 2$W)0! V2.?+0! '%! 7#*1#)+2+#&! 02! '0! 7#*1#-20*0&2! V:#'.2+3! ?0)! -V5+#&)! ?V)#-?#&&V0)! I.+! ).=+))0&2!.&0!2-%&)+2+#&!?.!?V)#-?-0!:0-)!'[#-?-0!02!'%!20&?%&70!V:#'.2+:0!?0)!AQ")!?%&)! '0)! C/B)! 7$0Z! '0)! 0.7%-6#20)! 5-\70! X! ?0)! *V2$#?0)! 02! ?0)! #.2+')! +&3#-*%2+I.0)N! D0! 7'%))0*0&2!=+#+&3#-*%2+I.0!?0)!1-#2V+&0)!$.*%+&0)!)0!1'+%&2!0&!)0!'+%&2!JR4K!0&!I.%2-0! 0&)0*='0)!J#-?#&&V0);!R4);!-V5+#&)!?V)#-?#&&V0)!I.+!0&2#.-0&2!'0)!R4);!02!'0)!%.2-0)! -V5+#&)!?V)#-?#&&V0)K!%!V2V!033072.V!1#.-!0M%*+&0-!)+!'%!7#*1#)+2+#&!02!'0!7#*1#-20*0&2! V:#'.2+3! J7$0Z! '0)! ?+33V-0&2)! :0-2V=-V0)! #-2$#'#5.0)K! )#&2! ?+33V-0&2! ?%&)! 70)! I.%2-0! 0&)0*='0)N! D[%&%'6)0! %! -V:V'V! I.0! 1%-! '%! 7#*1#)+2+#&;! '0)! -V5+#&)! #-?#&&V0)! ?0)! 1-#2V+&0)!)#&2!?+)2+&72)!?0)!2-#+)!%.2-0)!0&)0*='0);!*%+)!'0)!-V5+#&)!R4!*#&2-0&2!.&0! 7#&)0-:%2+#&!V:#'.2+:0!)+*+'%+-0!%.M!-V5+#&)!#-?#&&V0)N!D0)!-V5+#&)!?V)#-?#&&V0)!I.+! 0&2#.-0&2!'0)!-V5+#&)!R4!)#&2!1'.)!&V5%2+:0*0&2!7$%-5V0)!02!*#+&)!7#&)0-:V0)!I.0!'0.-)! -V5+#&)!R4!%?S%70&20)N!D0)!-V).'2%2)!1-V)0&2V)!).55W-0&2!'0!-]'0!S#.V!1%-!'0)!-V)+?.)! $6?-#1$+'0)!#.!7$%-5V)!%.2#.-!?0)!R4)!1#.-!1+'#20-!'0)!-V5+#&)!R4!:0-)!'0)!)+20)!?0!'+%+)#&! ! +++! ! ! ! ! ?0)! *#'V7.'0)! %))#7+V0)N! D%! 7#&&%+))%&70! 3#.-&+0! 1%-! '[%&%'6)0! ?0! 7#&)0-:%2+#&! V:#'.2+:0! 1#.-! '0)! R4)! 0&7#.-%50! X! V2.?+0-! .&0! I.0)2+#&! %))#7+V0;! X! )%:#+-! '%! 7#&)0-:%2+#&!V:#'.2+:0!?0)!AQ")!?%&)!'0)!C/A)TC/B);!7#*1%-V!%.M!AQ")!?0)!-V5+#&)! #-?#&&V0)N!/%&)!.&0!%.2-0!%11-#7$0!=+#+&3#-*%2+I.0;!'%!7#&)0-:%2+#&!02!'[V*0-50&70!?0! )+20)! ?0! *V2$6'%2+#&;! %7V26'%2+#&;! 02! .=+I.+2+&%2+#&! ?%&)! '0)! -V5+#&)! #-?#&&V0)! 02! ?V)#-?#&&V0)! #&2! V2V! V2.?+V0)! ).-! GG! 7'%?0)! V:#'.2+3)! 2-%&)*+)! ?01.+)! '0! ?#*%+&0! 0.7%-6#20! 0&2+0-! S.)I.[X! '%! ).10-3%*+''0! ?0)! 5-%&?)! )+&50)N! >0)! )+20)! )0! -0&7#&2-0&2! ).-2#.2!?%&)!'0)!-V)+?.)!%-5+&+&0!02!'6)+&0N!C'!%!V2V!*#&2-V!I.0!"@9!AQ"!S#.0!.&!-]'0! *%S0.-!?%&)!'%!7#&)0-:%2+#&!1#.-!'0)!%-5+&+&0)!02!'0)!'6)+&0)!X!'%!3#+)!?%&)!'0)!-V5+#&)! #-?#&&V0)!02!?V)#-?#&&V0);!?%&)!2#.)!'0)!GG!&+:0%.M;!?0!*%&+W-0!1'.)!)+5&+3+7%2+:0!?%&)! '0!7'%?0!?0)!*%**+3W-0)N!C'!%!V2V!*#&2-V!I.[.&!&#*=-0!)+5&+3+7%2+3!?0!&#.:0%.M!)+20)! "@9! '6)+&0! %11%-%^2! ?%&)! '0)! -V5+#&)! ?V)#-?#&&V0)! ?0)! 1-#2V+&0)! 7$0Z! '0)! ?0.2V-#)2#*0)!02!'0)!*%**+3W-0)N!/%&)!'0)!$+)2#&0);!'0)!)+20)!"@9!*#&2-0&2!.&!1%2-#&! ?0!7#&)0-:%2+#&!)+5&+3+7%2+:0*0&2!?+)2+&72!02!V:+?0&2!S.)I.0!7$0Z!'0!1'.)!'#+&2%+&!%&7Y2-0! 7#**.&!?0)!*%**+3W-0)N!/%&)!.&0!%&%'6)0!)V1%-V0!?0)!&+:0%.M!V:#'.2+3)!*.'2+1'0)!?0)! -V5+#&)! R4! $.*%+&0)! :V-+3+V0)! 0M1V-+*0&2%'0*0&2;! .&! 0&-+7$+))0*0&2! )+5&+3+7%2+3! ?0)! )+20)! ?[.=+I.+2+&%2+#&! 7#&)0-:V)! ?%&)! '0)! -V5+#&)! R4! %! V2V! ?V7#.:0-2! ?%&)! 2#.)! '0)! &+:0%.M!V:#'.2+3)!?0)!*%**+3W-0)N!/0!*%&+W-0!)+*+'%+-0;!'0)!-V5+#&)!R4!*#&2-0&2!.&0! 1-V3V-0&70!)+5&+3+7%2+:0!1#.-!'0)!)+20)!%:07!?0!*.'2+1'0)!*#?+3+7%2+#&)!"@9!I.%&?!0''0)! )#&2!2-%+2V0)!X!'%!3#+)!7#**0!?0)!-V5+#&)!#-?#&&V0)!#.!?V)#-?#&&V0)N!>0)!-V).'2%2)! +&?+I.0&2!'%!&V70))+2V!?0!7#&)+?V-0-!'[%&%'6)0!?0)!C/B)!X!?0)!&+:0%.M!V:#'.2+3)!*.'2+1'0)! %3+&! ?0! 7#*1-0&?-0! '0.-)! 1%2-#&)! V:#'.2+3)! 7#*1'0M0)N! D%! 1-V)0&20! V2.?0! ?%&)! )#&! ! +:! ! ! ! ! 0&)0*='0!?V*#&2-0!'%!7#*1#)+2+#&!?+)2+&720!0&!%7+?0)!%*+&V);!'%!1-V3V-0&70!AQ"!02!'%! 7#&)0-:%2+#&!?0)!C/B)!I.+!*#&2-0&2!?+33V-0&2!V2%2)!?0!7#&3#-*%2+#&!J0N5N;!?V)#-?#&&V0);! ?V)#-?#&&V0)!%.2#.-!?0)!R4!02!'0)!-V5+#&)!R4K;!02!'0)!+&20-P-0'%2+#&)!0&2-0!70)!1-#1-+V2V)N! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! :! ! ! ! ! ;?CDEFGHIJHBHD=<, ! R+-)2!%&?!3#-0*#)2;!C!O#.'?!'+(0!2#!0M1-0))!*6!?0010)2!5-%2+2.?0!2#!*6!).10-:+)#-! A-#30))#-!A%.'!_%--+)#&;!3#-!$+)!5.+?%&70;!*#2+:%2+#&!%&?!7#&2+&.#.)!).11#-2!?.-+&5!*6! )2.?+0)N! _0! +&2-#?.70?! *0! 2#! 2$0! 3%)7+&%2+&5! O#-'?! #3! +&2-+&)+7%''6! ?+)#-?0-0?! 1-#20+&)N! "#)2! #3! %'';! C! 2$%&(! $+*! 3#-! $+)! 1%2+0&70! %&?! 0&7#.-%50*0&2N! `#-(+&5! .&?0-! $+)! ).10-:+)+#&! +)! %! #&70P+&P%P'+302+*0! 0M10-+0&70! 3#-! *0N! _+)! +&)+5$23.'! 7#**0&2);! 7-+2+7%'! 2$+&(+&5!%&?!0M10-2+)0!$0'10?!*0!2#!+*1-#:0!*6!-0)0%-7$!+&!2$0!1%)2!3+:0!60%-)N! ! C! %*! 5-%203.'! 2#! 2$0! *0*=0-)! #3! *6! ).10-:+)#-6! 7#**+2200;! A-#3N! aV-]*0! `%'?+)1b$'! %&?! A-#3N! a%70(! "%S0O)(+! 3#-! 2$0! 5.+?%&70;! ).550)2+#&)! %&?! 3-.+23.'! ?+)7.))+#&)!?.-+&5!).10-:+)#-6!7#**+2200!*002+&5)N!! ! C!%*!0M2-0*0'6!5-%203.'!2#!2$0!4+#'#56!/01%-2*0&2!3#-!2$0!).11#-2!2#!7#*1'020!*6! 2$0)+)N!C!O#.'?!'+(0!2#!0)107+%''6!2$%&(!@&7+'!8+220&);!U.)%&!4#72+;!U.)%&!8%=0;!@&&0P "%-+0! Dc_0.-0.M;! U#&%'! A%20'! %&?! Q#&6! 3#-! 2$0+-! ).11#-2! +&! 2$0! 4+#'#56! /01%-2*0&2N! U107+%'!2$%&()!2#!UV=%)2+0&!A#-2%'+0-!3#-!2-%&)'%2+&5!*6!2$0)+)!%=)2-%72!+&2#!R-0&7$N! ! C!O#.'?!'+(0!2#!2$%&(!2$0!*0*=0-)!#3!>#*1.20!>%&%?%!%&?!>%'7.'!<.V=07!).11#-2! 5-#.1!3#-!2$0+-!1-#*12!-0)1#&)0)!%&?!1%2+0&70!+&!%&)O0-+&5!*6!I.0)2+#&)!%&?!-0I.0)2)N!! ! C!#O0!*6!)+&70-0!2$%&()!2#!*6!.&?0-5-%?.%20!*0&2#-!A-#3N!>NUN!A%-%*0)$O%-+!3#-!
Load more

Recommended publications
  • Identification and Characterisation of Human Cytomegalovirus-Mediated Degradation of Helicase-Like Transcription Factor
    Identification and Characterisation of Human Cytomegalovirus-Mediated Degradation of Helicase-Like Transcription Factor Kai-Min Lin Department of Medicine Cambridge Institute for Medical Research University of Cambridge This dissertation is submitted for the degree of Doctor of Philosophy Fitzwilliam College September 2020 Declaration I hereby declare, that except where specific reference is made to the work of others, the contents of this dissertation are original and have not been submitted in whole or in part for consideration for any other degree of qualification in this, or any other university. This dissertation is the result of my own work and includes nothing which is the outcome of work done in collaboration except as where specified in the text and acknowledgments. This dissertation does not exceed the specified word limit of 60,000 words as defined by the Degree Committee, excluding figures, photographs, tables, appendices and bibliography. Kai-Min Lin September, 2020 I Summary Identification and characterisation of human cytomegalovirus-mediated degradation of helicase-like transcription factor Kai-Min Lin Viruses are known to degrade host factors that are important in innate antiviral immunity in order to infect successfully. To systematically identify host proteins targeted for early degradation by human cytomegalovirus (HCMV), the lab developed orthogonal screens using high resolution multiplexed mass spectrometry. Taking advantage of broad and selective proteasome and lysosome inhibitors, proteasomal degradation was found to be heavily exploited by HCMV. Several known antiviral restriction factors, including components of cellular promyelocytic leukemia (PML) were enriched in a shortlist of proteasomally degraded proteins during infection. A particularly robust novel ‘hit’ was helicase-like transcription factor (HLTF), a DNA repair protein that participates in error-free repair of stalled replication forks.
    [Show full text]
  • A New Census of Protein Tandem Repeats and Their Relationship with Intrinsic Disorder
    G C A T T A C G G C A T genes Article A New Census of Protein Tandem Repeats and Their Relationship with Intrinsic Disorder Matteo Delucchi 1,2 , Elke Schaper 1,2,† , Oxana Sachenkova 3,‡, Arne Elofsson 3 and Maria Anisimova 1,2,* 1 ZHAW Life Sciences und Facility Management, Applied Computational Genomics, 8820 Wädenswil, Switzerland; [email protected] 2 Swiss Institute of Bioinformatics, 1015 Lausanne, Switzerland 3 Science of Life Laboratory, Department of Biochemistry and Biophysics, Stockholm University, 106 91 Stockholm, Sweden * Correspondence: [email protected]; Tel.: +41-(0)58-934-5882 † Present address: Carbon Delta AG, 8002 Zürich, Switzerland. ‡ Present address: Vildly AB, 385 31 Kalmar, Sweden. Received: 9 March 2020; Accepted: 1 April 2020; Published: 9 April 2020 Abstract: Protein tandem repeats (TRs) are often associated with immunity-related functions and diseases. Since that last census of protein TRs in 1999, the number of curated proteins increased more than seven-fold and new TR prediction methods were published. TRs appear to be enriched with intrinsic disorder and vice versa. The significance and the biological reasons for this association are unknown. Here, we characterize protein TRs across all kingdoms of life and their overlap with intrinsic disorder in unprecedented detail. Using state-of-the-art prediction methods, we estimate that 50.9% of proteins contain at least one TR, often located at the sequence flanks. Positive linear correlation between the proportion of TRs and the protein length was observed universally, with Eukaryotes in general having more TRs, but when the difference in length is taken into account the difference is quite small.
    [Show full text]
  • Intrinsic Disorder in Tetratricopeptide Repeat Proteins
    International Journal of Molecular Sciences Article Intrinsic Disorder in Tetratricopeptide Repeat Proteins 1, 1, 1, 2 Nathan W. Van Bibber y, Cornelia Haerle y, Roy Khalife y, Bin Xue and Vladimir N. Uversky 1,3,4,* 1 Department of Molecular Medicine Morsani College of Medicine, University of South Florida, 12901 Bruce B. Downs Blvd., Tampa, FL 33612, USA; [email protected] (N.W.V.B.); [email protected] (C.H.); [email protected] (R.K.) 2 Department of Cell Biology, Microbiology and Molecular Biology, School of Natural Sciences and Mathematics, College of Arts and Sciences, University of South Florida, Tampa, FL 33620, USA; [email protected] 3 USF Health Byrd Alzheimer’s Research Institute, Morsani College of Medicine, University of South Florida, 12901 Bruce B. Downs Blvd., Tampa, FL 33612, USA 4 Institute for Biological Instrumentation, Russian Academy of Sciences, Federal Research Center “Pushchino Scientific Center for Biological Research of the Russian Academy of Sciences”, 4 Institutskaya St., Pushchino, 142290 Moscow Region, Russia * Correspondence: [email protected]; Tel.: +1-813-974-5816; Fax: +1-813-974-7357 These authors contributed equally to this work. y Received: 21 April 2020; Accepted: 22 May 2020; Published: 25 May 2020 Abstract: Among the realm of repeat containing proteins that commonly serve as “scaffolds” promoting protein-protein interactions, there is a family of proteins containing between 2 and 20 tetratricopeptide repeats (TPRs), which are functional motifs consisting of 34 amino acids. The most distinguishing feature of TPR domains is their ability to stack continuously one upon the other, with these stacked repeats being able to affect interaction with binding partners either sequentially or in combination.
    [Show full text]
  • Repeatsdb in 2021: Improved Data And
    RepeatsDB in 2021: improved data and extended classification for protein tandem repeat structures Lisanna Paladin, Martina Bevilacqua, Sara Errigo, Damiano Piovesan, Ivan Mičetić, Marco Necci, Alexander Miguel Monzon, Maria Laura Fabre, Jose luis Lopez, Juliet Nilsson, et al. To cite this version: Lisanna Paladin, Martina Bevilacqua, Sara Errigo, Damiano Piovesan, Ivan Mičetić, et al.. RepeatsDB in 2021: improved data and extended classification for protein tandem repeat structures. Nucleic Acids Research, Oxford University Press, 2020, 10.1093/nar/gkaa1097. hal-03089312 HAL Id: hal-03089312 https://hal.archives-ouvertes.fr/hal-03089312 Submitted on 4 Jan 2021 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Page 1 of 11 Nucleic Acids Research 1 2 RepeatsDB in 2021: improved data and 3 4 5 extended classification for protein tandem 6 7 repeat structures 8 9 10 Lisanna Paladin1, Martina Bevilacqua1, Sara Errigo1, Damiano Piovesan1, Ivan Mičetić1, Marco Necci1, 11 Alexander Miguel Monzon1, Maria Laura Fabre2, Jose Luis Lopez2, Juliet F. Nilsson2, Javier Rios3, Pablo 12 3 3 3 4 13 Lorenzano Menna , Maia Cabrera , Martin Gonzalez Buitron , Mariane Gonçalves Kulik , Sebastian 14 Fernandez-Alberti3, Maria Silvina Fornasari3, Gustavo Parisi3, Antonio Lagares2, Layla Hirsh5, Miguel A.
    [Show full text]
  • Intrinsic Disorder of the BAF Complex: Roles in Chromatin Remodeling and Disease Development
    International Journal of Molecular Sciences Article Intrinsic Disorder of the BAF Complex: Roles in Chromatin Remodeling and Disease Development Nashwa El Hadidy 1 and Vladimir N. Uversky 1,2,* 1 Department of Molecular Medicine, Morsani College of Medicine, University of South Florida, 12901 Bruce B. Downs Blvd. MDC07, Tampa, FL 33612, USA; [email protected] 2 Laboratory of New Methods in Biology, Institute for Biological Instrumentation of the Russian Academy of Sciences, Federal Research Center “Pushchino Scientific Center for Biological Research of the Russian Academy of Sciences”, Pushchino, 142290 Moscow Region, Russia * Correspondence: [email protected]; Tel.: +1-813-974-5816; Fax: +1-813-974-7357 Received: 20 September 2019; Accepted: 21 October 2019; Published: 23 October 2019 Abstract: The two-meter-long DNA is compressed into chromatin in the nucleus of every cell, which serves as a significant barrier to transcription. Therefore, for processes such as replication and transcription to occur, the highly compacted chromatin must be relaxed, and the processes required for chromatin reorganization for the aim of replication or transcription are controlled by ATP-dependent nucleosome remodelers. One of the most highly studied remodelers of this kind is the BRG1- or BRM-associated factor complex (BAF complex, also known as SWItch/sucrose non-fermentable (SWI/SNF) complex), which is crucial for the regulation of gene expression and differentiation in eukaryotes. Chromatin remodeling complex BAF is characterized by a highly polymorphic structure, containing from four to 17 subunits encoded by 29 genes. The aim of this paper is to provide an overview of the role of BAF complex in chromatin remodeling and also to use literature mining and a set of computational and bioinformatics tools to analyze structural properties, intrinsic disorder predisposition, and functionalities of its subunits, along with the description of the relations of different BAF complex subunits to the pathogenesis of various human diseases.
    [Show full text]
  • ST Proteins, a New Family of Plant Tandem Repeat Proteins with A
    Albornos et al. BMC Plant Biology 2012, 12:207 http://www.biomedcentral.com/1471-2229/12/207 RESEARCH ARTICLE Open Access ST proteins, a new family of plant tandem repeat proteins with a DUF2775 domain mainly found in Fabaceae and Asteraceae Lucía Albornos, Ignacio Martín, Rebeca Iglesias, Teresa Jiménez, Emilia Labrador and Berta Dopico* Abstract Background: Many proteins with tandem repeats in their sequence have been described and classified according to the length of the repeats: I) Repeats of short oligopeptides (from 2 to 20 amino acids), including structural cell wall proteins and arabinogalactan proteins. II) Repeats that range in length from 20 to 40 residues, including proteins with a well-established three-dimensional structure often involved in mediating protein-protein interactions. (III) Longer repeats in the order of 100 amino acids that constitute structurally and functionally independent units. Here we analyse ShooT specific (ST) proteins, a family of proteins with tandem repeats of unknown function that were first found in Leguminosae, and their possible similarities to other proteins with tandem repeats. Results: ST protein sequences were only found in dicotyledonous plants, limited to several plant families, mainly the Fabaceae and the Asteraceae. ST mRNAs accumulate mainly in the roots and under biotic interactions. Most ST proteins have one or several Domain(s) of Unknown Function 2775 (DUF2775). All deduced ST proteins have a signal peptide, indicating that these proteins enter the secretory pathway, and the mature proteins have tandem repeat oligopeptides that share a hexapeptide (E/D)FEPRP followed by 4 partially conserved amino acids, which could determine a putative N-glycosylation signal, and a fully conserved tyrosine.
    [Show full text]
  • Repeatsdb-Lite: a Web Server for Unit Annotation of Tandem Repeat Proteins Layla Hirsh1,2,†, Lisanna Paladin1,†, Damiano Piovesan1 and Silvio C
    W402–W407 Nucleic Acids Research, 2018, Vol. 46, Web Server issue Published online 9 May 2018 doi: 10.1093/nar/gky360 RepeatsDB-lite: a web server for unit annotation of tandem repeat proteins Layla Hirsh1,2,†, Lisanna Paladin1,†, Damiano Piovesan1 and Silvio C. E. Tosatto1,3,* 1Dept. of Biomedical Sciences, University of Padua, Padua, Italy, 2Dept. of Engineering, Pontificia Universidad Catolica´ del Peru,´ Lima, Peru´ and 3CNR Institute of Neurosciences, Padua, Italy Received March 06, 2018; Revised April 13, 2018; Editorial Decision April 23, 2018; Accepted April 24, 2018 ABSTRACT structural topology (4) as elongated, closed or ‘beads on a string’ (3). A finer classification is possible considering the RepeatsDB-lite (http://protein.bio.unipd.it/ type and length of the composing units (3). Subtle differ- repeatsdb-lite) is a web server for the predic- ences in the structural conformation of the units give rise tion of repetitive structural elements and units in to large differences in shape and structural properties of tandem repeat (TR) proteins. TRs are a widespread the whole protein, including curvature and twist (6). For but poorly annotated class of non-globular proteins examples, families of closed structures are likely to con- carrying heterogeneous functions. RepeatsDB-lite serve the number of units due to spatial constraints and are extends the prediction to all TR types and strongly quite rigid. Elongated structures like solenoids are in gen- improves the performance both in terms of compu- eral more flexible and the secondary structure and shape of tational time and accuracy over previous methods, the units provides a way to fine tune global properties (7).
    [Show full text]
  • Self-Analysis of Repeat Proteins Reveals Evolutionarily Conserved
    Merski et al. BMC Bioinformatics (2020) 21:179 https://doi.org/10.1186/s12859-020-3493-y RESEARCH ARTICLE Open Access Self-analysis of repeat proteins reveals evolutionarily conserved patterns Matthew Merski1*† , Krzysztof Młynarczyk1†, Jan Ludwiczak2,3, Jakub Skrzeczkowski1, Stanisław Dunin-Horkawicz2 and Maria W. Górna1* * Correspondence: merski@gmail. com; [email protected] Abstract †Matthew Merski and Krzysztof Młynarczyk contributed equally to Background: Protein repeats can confound sequence analyses because the this work. repetitiveness of their amino acid sequences lead to difficulties in identifying whether 1Structural Biology Group, Biological similar repeats are due to convergent or divergent evolution. We noted that the and Chemical Research Centre, “ ” Department of Chemistry, University patterns derived from traditional dot plot protein sequence self-similarity analysis of Warsaw, Warsaw, Poland tended to be conserved in sets of related repeat proteins and this conservation could Full list of author information is be quantitated using a Jaccard metric. available at the end of the article Results: Comparison of these dot plots obviated the issues due to sequence similarity for analysis of repeat proteins. A high Jaccard similarity score was suggestive of a conserved relationship between closely related repeat proteins. The dot plot patterns decayed quickly in the absence of selective pressure with an expected loss of 50% of Jaccard similarity due to a loss of 8.2% sequence identity. To perform method testing, we assembled a standard set of 79 repeat proteins representing all the subgroups in RepeatsDB. Comparison of known repeat and non-repeat proteins from the PDB suggested that the information content in dot plots could be used to identify repeat proteins from pure sequence with no requirement for structural information.
    [Show full text]
  • Self-Analysis of Repeat Proteins Reveals Evolutionarily Conserved Patterns
    Self-Analysis of Repeat Proteins Reveals Evolutionarily Conserved Patterns Matthew Merski ( [email protected] ) Uniwersytet Warszawski https://orcid.org/0000-0002-1844-6997 Krzysztof Młynarczyk Uniwersytet Warszawski Jan Ludwiczak Uniwersytet Warszawski Jakub Skrzeczkowski Uniwersytet Warszawski Stanisław Dunin-Horkawicz Uniwersytet Warszawski Maria W. Górna Uniwersytet Warszawski Research article Keywords: protein repeat, repeat identication, structural bioinformatics, protein evolution Posted Date: April 16th, 2020 DOI: https://doi.org/10.21203/rs.2.15797/v4 License: This work is licensed under a Creative Commons Attribution 4.0 International License. Read Full License Version of Record: A version of this preprint was published at BMC Bioinformatics on May 7th, 2020. See the published version at https://doi.org/10.1186/s12859-020-3493-y. Page 1/23 Abstract Background: Protein repeats can confound sequence analyses because the repetitiveness of their amino acid sequences lead to diculties in identifying whether similar repeats are due to convergent or divergent evolution. We noted that the patterns derived from traditional “dot plot” protein sequence self- similarity analysis tended to be conserved in sets of related repeat proteins and this conservation could be quantitated using a Jaccard metric. Results: Comparison of these dot plots obviated the issues due to sequence similarity for analysis of repeat proteins. A high Jaccard similarity score was suggestive of a conserved relationship between closely related repeat proteins. The dot plot patterns decayed quickly in the absence of selective pressure with an expected loss of 50% of Jaccard similarity due to a loss of 8.2 % sequence identity. To perform method testing, we assembled a standard set of 79 repeat proteins representing all the subgroups in RepeatsDB.
    [Show full text]
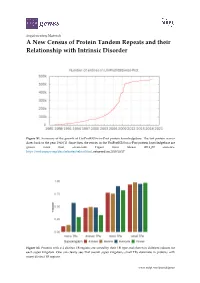
  • A New Census of Protein Tandem Repeats and Their Relationship with Intrinsic Disorder
    Supplementary Materials A New Census of Protein Tandem Repeats and their Relationship with Intrinsic Disorder Figure S1. Summary of the growth of UniProtKB/Swiss‐Prot protein knowledgebase. The last protein census dates back to the year 1999 [1]. Since then, the entries in the UniProtKB/Swiss‐Prot protein knowledgebase are grown more than seven‐fold. Figure from release 2018_09 statistics. https://web.expasy.org/docs/relnotes/relstat.html, retrieved on 2018/10/17. Figure S2. Proteins with ≥ 4 distinct TR regions are sorted by their TR type and shown in different colours for each super kingdom. One can clearly see, that overall super kingdoms small TRs dominate in proteins with many distinct TR regions. www.mdpi.com/journal/genes 2 of 8 Figure S3. The fraction of proteins containing TRs overall protein entries in UniProtKB/Swiss‐Prot is shown for a selection of heavily investigated species and displayed as function of the mean protein length. The tendency of more complex organisms having more and longer TRs can be seen. Figure S4. The fraction of proteins with homo TRs as a function of sequence length by kingdom resulting in a linear relationship. 3 of 8 Figure S5. The fraction of proteins with micro TRs as a function of sequence length by kingdom resulting in a linear relationship. Figure S6. The fraction of proteins with small TRs as a function of sequence length by kingdom resulting in a linear relationship. 4 of 8 Figure S7. The fraction of proteins with domain TRs as a function of sequence length by kingdom resulting in a linear relationship.
    [Show full text]
  • Protein Tandem Repeats - the More Perfect, the Less Structured
    Protein tandem repeats - the more perfect, the less structured. Julien Jorda, Bin Xue, Vladimir N Uversky, Andrey V Kajava To cite this version: Julien Jorda, Bin Xue, Vladimir N Uversky, Andrey V Kajava. Protein tandem repeats - the more perfect, the less structured.. FEBS Journal, Wiley, 2010, epub ahead of print. 10.1111/j.1742- 4658.2010.07684.x. hal-00491996 HAL Id: hal-00491996 https://hal.archives-ouvertes.fr/hal-00491996 Submitted on 10 Nov 2010 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Protein tandem repeats: the more perfect the less structured Julien Jorda1, Bin Xue2,3, Vladimir N. Uversky2-5, Andrey V. Kajava1,* 1Centre de Recherches de Biochimie Macromoléculaire, CNRS UMR-5237, University of Montpellier 1 and 2, Montpellier, France; 2Center for Computational Biology and Bioinformatics, Indiana University School of Medicine, Indianapolis, IN 46202, USA; 3Institute for Intrinsically Disordered Protein Research, Indiana University School of Medicine, Indianapolis, IN 46202, USA; 4Institute for Biological Instrumentation, Russian Academy of Sciences, 142290 Pushchino, Moscow Region, Russia; 5Department of Biochemistry and Molecular Biology, Indiana University School of Medicine, Indianapolis, IN 46202, USA Running title: Structural state of perfect protein repeats Keywords: bioinformatics, disordered conformation, evolution, sequence analysis, protein structure.
    [Show full text]
  • Disentangling the Complexity of Low Complexity Proteins
    Briefings in Bioinformatics, 21(2), 2020, 458–472 doi: 10.1093/bib/bbz007 Advance Access Publication Date: 30 January 2019 Review article Disentangling the complexity of low complexity proteins Pablo Mier , Lisanna Paladin, Stella Tamana, Sophia Petrosian, Borbála Hajdu-Soltész, Annika Urbanek, Aleksandra Gruca, Dariusz Plewczynski, Marcin Grynberg, Pau Bernadó, Zoltán Gáspári, Christos A. Ouzounis, Vasilis J. Promponas, Andrey V. Kajava, John M. Hancock, Silvio C. E. Tosatto , Zsuzsanna Dosztanyi and Miguel A. Andrade-Navarro Corresponding author: Pablo Mier, Faculty of Biology, Johannes Gutenberg University Mainz Hans-Dieter-Hüsch-Weg 15, 55128 Mainz, Germany. Tel.: +49-6131-39-21580; E-mail: [email protected] Pablo Mier is a postdoctoral researcher interested in the development of Web tools and databases related to protein evolution and low-complexity regions. He works in the Faculty of Biology at Johannes Gutenberg University Mainz. Lisanna Paladin is a PhD student of Biomedical Sciences Department at University of Padova. Her research focuses on tools and databases development for the description of non-globular proteins structure and function. Stella Tamana is a PhD candidate at the Department of Biological Sciences, University of Cyprus, where she studies bioinformatics. She is interested in the study of compositionally biased regions in protein sequences, the elucidation of their structural and functional properties and their handling in automated comparative genomics pipelines. Sophia Petrosian was a final-year student at the Biological Computation and Process Laboratory, Thessalonica, Greece. Borbála Hajdu-Soltész is a PhD student at the Eötvös Loránd University, Budapest, Hungary. She is a computational biologist interested in protein disorder and questions such as how do disorder properties contribute to cancer development.
    [Show full text]