DOCSLIB.ORG

The Topological Suceptibility of QCD at High Temperatures

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Topological Suceptibility of QCD at High Temperatures The Topological Susceptibility of QCD at High Temperatures Die topologische Suszeptibilität der QCD bei hohen Temperaturen Zur Erlangung des Grades eines Doktors der Naturwissenschaften (Dr. rer. nat.) genehmigte Dissertation von Peter Thomas Jahn Tag der Einreichung: 15.10.2019, Tag der Prüfung: 27.11.2019 Darmstadt — D 17 1. Gutachten: Prof. Ph.D. Guy D. Moore 2. Gutachten: Prof. Dr. rer. nat. Jens Braun Fachbereich Physik Institut für Kernphysik Theoriezentrum – AG Moore The Topological Susceptibility of QCD at High Temperatures Die topologische Suszeptibilität der QCD bei hohen Temperaturen Genehmigte Dissertation von Peter Thomas Jahn 1. Gutachten: Prof. Ph.D. Guy D. Moore 2. Gutachten: Prof. Dr. rer. nat. Jens Braun Tag der Einreichung: 15.10.2019 Tag der Prüfung: 27.11.2019 Darmstadt — D 17 Bitte zitieren Sie dieses Dokument als: URN: urn:nbn:de:tuda-tuprints-94854 URL: http://tuprints.ulb.tu-darmstadt.de/id/eprint/9485 Dieses Dokument wird bereitgestellt von tuprints, E-Publishing-Service der TU Darmstadt http://tuprints.ulb.tu-darmstadt.de [email protected] Die Veröffentlichung steht unter folgender Creative Commons Lizenz: Namensnennung – Nicht kommerziell – Keine Bearbeitungen 4.0 International https://creativecommons.org/licenses/by-nc-nd/4.0/ To Klary who passed away way too early. I’ve never met a cat as good-hearted and lively as you. Erklärung zur Dissertation Hiermit versichere ich, dass ich die vorliegende Dissertation selbstständig angefertigt und keine anderen als die angegebenen Quellen und Hilfsmittel verwendet habe. Alle wörtlichen und paraphrasierten Zitate wurden angemessen kenntlich gemacht. Die Ar- beit hat bisher noch nicht zu Prüfungszwecken gedient. Darmstadt, den 06. Dezember 2019 (Peter Thomas Jahn) Abstract Two of the most challenging problems in modern physics are the origin of dark matter and the strong CP problem. The latter means the non-observation of the violation of the combined particle-antiparticle and parity (CP) symmetries by the strong interaction which is conceptually allowed. Both problems – although prima facie disparate – could be simultaneously solved by the Peccei-Quinn mechanism. This results in a new particle, the axion. Despite strong experimental efforts, the discovery of the axion is yet to come, making precise theoretical predictions of its properties, especially its mass, highly valu- able. The axion’s properties are closely related to the topological structure of the vacuum of quantum chromodynamics (QCD). The QCD vacuum exhibits topologically non-trivial fluctuations of the gauge fields with the most important fluctuations being instantons. These topological fluctuations are quan- tified by the topological susceptibility χtop that controls the axion mass and therefore is – especially at high temperatures – an important input for axion cosmology. Since topological effects are inherently non-perturbative, lattice QCD is particularly suitable for precisely determining χtop. However, lattice simulations become extremely challenging at high temperatures because χtop is very suppressed. In this work, we develop and establish a novel method based on a combination of gradient flow and reweight- ing that artificially enhances the number of instantons and therefore allows to determine χtop at high temperatures. For computational simplicity, we content ourselves to pure SU(3) Yang-Mills theory for developing the method, but it is explicitly designed to be applicable also in full QCD. In particular, we provide a discretization of the instanton that allows for an analysis of the lattice-spacing effects on a lattice study of χtop. We then present the reweighting method that is eventually used to determine χtop up to 2 GeV in pure SU(3) Yang-Mills theory which constitutes the first direct determination of χtop at such high temperatures. Zusammenfassung Zwei der spannendsten Probleme der modernen Physik sind der Ursprung der dunklen Materie und das starke CP-Problem. Letzteres beschreibt die Nichtbeobachtung einer Verletzung der kombinierten Teilchen-Antiteilchen- und Parität (CP)-Symmetrien durch die starke Wechselwirkung, die grundsätz- lich erlaubt ist. Beide Probleme – obwohl a priori unterschiedlich – könnten gleichzeitig durch den Peccei-Quinn-Mechanismus gelöst werden. Dieser postuliert das Axion als neues Elementarteilchen. Trotz starker experimenteller Bemühungen steht die Entdeckung des Axions noch aus, sodass präzise theoretische Vorhersagen über dessen Eigenschaften, insbesondere dessen Masse, sehr wertvoll sind. Die Axioneigenschaften sind eng mit der topologischen Struktur des Vakuums der Quantenchromody- namik (QCD) verknüpft. Das QCD-Vakuum weist topologisch nichttriviale Fluktuationen der Eichfelder auf, quantifiziert durch die topologische Suszeptibilität χtop, welche die Axionenmasse kontrolliert und daher – insbesondere bei hohen Temperaturen – ein wichtiger Parameter für die Axionkosmologie ist. Die wichtigsten Fluktuationen sind dabei Instantone. Da topologische Effekte intrinsisch nichtperturba- tiv sind, eignen sich Gittersimulationen besonders gut zur präzisen Bestimmung von χtop. Diese werden jedoch bei hohen Temperaturen sehr anspruchsvoll, da χtop stark unterdrückt ist. In dieser Arbeit stellen wir eine neue Methode vor, basierend auf einer Kombination aus Gradientenfluss und Regewichtung, die die Anzahl der Instantone künstlich erhöht und es daher ermöglicht, χtop bei hohen Temperaturen zu bestimmen. Zur Entwicklung der Methode beschränken wir uns auf SU(3) Yang-Mills-Theorie, was numerisch deutlich günstiger ist. Die Methode ist jedoch so konzipiert, dass sie auch auf volle QCD angewandt werden kann. Insbesondere entwickeln wir eine Diskretisierung des Instantons, was eine Analyse der Diskretisierungseffekte bei eine Gitterberechnung von χtop ermöglicht. Weitherin stellen wir die Regewichtungs-Methode vor, die schließlich verwendet wird, um χtop bis zu Temperaturen von 2 GeV in reiner SU(3) Yang-Mills-Theorie zu bestimmen, was die erste direkte Bestimmung von χtop bei solch hohen Temperaturen darstellt. Contents 1. Introduction 1 2. Quantum Chromodynamics 11 2.1. The QCD Lagrangian........................................... 11 2.2. Path Integral Formalism and Thermal Field Theory........................ 14 2.3. Chiral Symmetry and the Chiral Anomaly.............................. 17 2.4. Topology and the QCD Vacuum..................................... 19 2.4.1. Instantons and the Vacuum Structure of QCD....................... 20 2.4.2. The Theta Vacua......................................... 30 2.4.3. The Topological Susceptibility................................ 31 2.4.4. The Dilute Instanton Gas................................... 33 3. Lattice Gauge Theory 37 3.1. Basic Concepts of Lattice Gauge Theory............................... 37 3.2. Pure Gauge Theory on the Lattice................................... 38 3.3. Symanzik Improvement Program................................... 40 3.4. The Lattice Field-Strength Tensor................................... 41 3.4.1. Clover Field-Strength Tensor.................................. 42 3.4.2. Improved Field-Strength Tensor................................ 42 3.4.3. The Topological Charge..................................... 43 3.5. Gradient Flow............................................... 44 3.5.1. Wilson Flow............................................ 45 3.5.2. Zeuthen Flow........................................... 46 3.6. Scale Setting................................................ 48 3.7. Monte Carlo Simulations........................................ 49 3.7.1. Hybrid Monte Carlo Algorithm................................ 51 3.8. Autocorrelation and Error Analysis.................................. 53 3.8.1. Binning and Jackknife...................................... 54 3.8.2. Example of a Statistical Analysis............................... 54 4. Topological Configurations on the Lattice 57 4.1. Instanton and Caloron Discretization................................. 58 4.2. Lattice Instanton and Caloron Properties.............................. 60 4.2.1. Caloron vs. Instanton...................................... 60 4.2.2. Actions............................................... 61 4.2.3. Topological Charges....................................... 62 4.2.4. Critical Radius.......................................... 63 4.3. Estimated a2 Errors in the Topological Susceptibility....................... 65 4.4. Conclusions................................................. 68 5. The Topological Susceptibility via Reweighting 69 5.1. The Reweighting Method........................................ 70 5.1.1. Definition of Reweighting................................... 70 5.1.2. Choice of Reweighting Variable................................ 71 5.1.3. Updating with an Arbitrary Weight Function....................... 71 5.1.4. Building the Reweighting Function............................. 72 5.1.5. Parameters to Tune....................................... 75 5.2. Results.................................................... 76 5.3. Discussion.................................................. 81 6. Improvement of the Reweighting Method: χtop up to 2 GeV 85 6.1. The Method................................................ 85 6.1.1. The Low Barrier......................................... 85 6.1.2. The High Barrier......................................... 87 6.1.3. The Middle Region....................................... 88 6.1.4. Reweighting with Multiple Regions.............................. 88 6.1.5. Parameters to Tune......................................
Load more

Recommended publications
  • Vacuum As a Physical Medium
    cu - TP - 626 / EERNIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII I.12RI=IR1I;s. QI.; 621426 VACUUM AS A PHYSICAL MEDIUM (RELATIVISTIC HEAVY ION COLLISIONS AND THE BOLTZMANN EQUAT ION) T. D. LEE COLUMBIA UNIvERsI1Y, New Y0RI<, N.Y. 10027 A LECTURE GIVEN AT THE INTERNATIONAL SYMPOSIUM IN HONOUR OF BOLTZMANN'S 1 50TH BIRTHDAY, FEBRUARY 1994. THIS RESEARCH WAS SUPPORTED IN PART BY THE U.S. DEPARTMENT OF ENERGY. OCR Output OCR OutputVACUUM AS A PHYSICAL MEDIUM (Relativistic Heavy Ion Collisions and the Boltzmann Equation) T. D. Lee Columbia University, New York, N.Y. 10027 It is indeed a privilege for me to attend this international symposium in honor of Boltzmann's 150th birthday. ln this lecture, I would like to cover the following topics: 1) Symmetries and Asymmetries: Parity P (right—left symmetry) Charge conjugation C (particle-antiparticle symmetry) Time reversal T Their violations and CPT symmetry. 2) Two Puzzles of Modern Physics: Missing symmetry Vacuum as a physical medium Unseen quarks. 3) Relativistic Heavy Ion Collisions (RHIC): How to excite the vacuum? Phase transition of the vacuum Hanbury-Brown-Twiss experiments. 4) Application of the Relativistic Boltzmann Equations: ARC model and its Lorentz invariance AGS experiments and physics in ultra-heavy nuclear density. OCR Output One of the underlying reasons for viewing the vacuum as a physical medium is the discovery of missing symmetries. I will begin with the nonconservation of parity, or the asymmetry between right and left. ln everyday life, right and left are obviously distinct from each other. Our hearts, for example, are usually not on the right side. The word right also means "correct,' right? The word sinister in its Latin root means "left"; in Italian, "left" is sinistra.
    [Show full text]
  • Arxiv:1202.1557V1
    The Heisenberg-Euler Effective Action: 75 years on ∗ Gerald V. Dunne Physics Department, University of Connecticut, Storrs, CT 06269-3046, USA On this 75th anniversary of the publication of the Heisenberg-Euler paper on the full non- perturbative one-loop effective action for quantum electrodynamics I review their paper and discuss some of the impact it has had on quantum field theory. I. HISTORICAL CONTEXT After the 1928 publication of Dirac’s work on his relativistic theory of the electron [1], Heisenberg immediately appreciated the significance of the new ”hole theory” picture of the quantum vacuum of quantum electrodynamics (QED). Following some confusion, in 1931 Dirac associated the holes with positively charged electrons [2]: A hole, if there were one, would be a new kind of particle, unknown to experimental physics, having the same mass and opposite charge to an electron. With the discovery of the positron in 1932, soon thereafter [but, interestingly, not immediately [3]], Dirac proposed at the 1933 Solvay Conference that the negative energy solutions [holes] should be identified with the positron [4]: Any state of negative energy which is not occupied represents a lack of uniformity and this must be shown by observation as a kind of hole. It is possible to assume that the positrons are these holes. Positron theory and QED was born, and Heisenberg began investigating positron theory in earnest, publishing two fundamental papers in 1934, formalizing the treatment of the quantum fluctuations inherent in this Dirac sea picture of the QED vacuum [5, 6]. It was soon realized that these quantum fluctuations would lead to quantum nonlinearities [6]: Halpern and Debye have already independently drawn attention to the fact that the Dirac theory of the positron leads to the scattering of light by light, even when the energy of the photons is not sufficient to create pairs.
    [Show full text]
  • Simple Model for the QCD Vacuum
    A1110? 31045(3 NBSIR 83-2759 Simple Model for the QCD Vacuum U S. DEPARTMENT OF COMMERCE National Bureau of Standards Center for Radiation Research Washington, DC 20234 Centre d'Etudes de Bruyeres-le-Chatel 92542 Montrouge CEDEX, France July 1983 U S. DEPARTMENT OF COMMERCE NATIONAL BUREAU OF STANOAROS - - - i rx. NBSIR 83-2759 SIMPLE MODEL FOR THE QCD VACUUM m3 C 5- Michael Danos U S DEPARTMENT OF COMMERCE National Bureau of Standards Center for Radiation Research Washington, DC 20234 Daniel Gogny and Daniel Irakane Centre d'Etudes de Bruyeres-le-Chatel 92542 Montrouge CEDEX, France July 1983 U.S. DEPARTMENT OF COMMERCE, Malcolm Baldrige, Secretary NATIONAL BUREAU OF STANDARDS, Ernest Ambler, Director SIMPLE MODEL FOR THE QCD VACUUM Michael Danos, Nastional Bureau of Standards, Washington, D.C. 20234, USA and Daniel Gogny and Daniel Irakane Centre d' Etudes de Bruyeres-le-Chatel , 92542 Montrouge CEDEX, France Abstract B.v treating the high-momentum gluon and the quark sector as an in principle calculable effective Lagrangian we obtain a non-perturbati ve vacuum state for OCD as an infrdred gluon condensate. This vacuum is removed from the perturbative vacuum by an energy gap and supports a Meissner-Ochsenfeld effect. It is unstable below a minimum size and it also suggests the existence of a universal hadroni zation time. This vacuum thus exhibits all the properties required for color confinement. I. Introduction By now it is widely believed that the confinement in QCD, in analogy with superconductivity, results from the existence of a physical vacuum which is removed from the remainder of the spectrum by an energy density gap and which exhibits a Meissner-Ochsenfeld effect.
    [Show full text]
  • Vacuum Energy
    Vacuum Energy Mark D. Roberts, 117 Queen’s Road, Wimbledon, London SW19 8NS, Email:[email protected] http://cosmology.mth.uct.ac.za/ roberts ∼ February 1, 2008 Eprint: hep-th/0012062 Comments: A comprehensive review of Vacuum Energy, which is an extended version of a poster presented at L¨uderitz (2000). This is not a review of the cosmolog- ical constant per se, but rather vacuum energy in general, my approach to the cosmological constant is not standard. Lots of very small changes and several additions for the second and third versions: constructive feedback still welcome, but the next version will be sometime in coming due to my sporadiac internet access. First Version 153 pages, 368 references. Second Version 161 pages, 399 references. arXiv:hep-th/0012062v3 22 Jul 2001 Third Version 167 pages, 412 references. The 1999 PACS Physics and Astronomy Classification Scheme: http://publish.aps.org/eprint/gateway/pacslist 11.10.+x, 04.62.+v, 98.80.-k, 03.70.+k; The 2000 Mathematical Classification Scheme: http://www.ams.org/msc 81T20, 83E99, 81Q99, 83F05. 3 KEYPHRASES: Vacuum Energy, Inertial Mass, Principle of Equivalence. 1 Abstract There appears to be three, perhaps related, ways of approaching the nature of vacuum energy. The first is to say that it is just the lowest energy state of a given, usually quantum, system. The second is to equate vacuum energy with the Casimir energy. The third is to note that an energy difference from a complete vacuum might have some long range effect, typically this energy difference is interpreted as the cosmological constant.
    [Show full text]
  • Quantum Optics Properties of QCD Vacuum
    EPJ Web of Conferences 164, 07030 (2017) DOI: 10.1051/epjconf/201716407030 ICNFP 2016 EPJ Web of Conferences will be set by the publisher DOI: will be set by the publisher c Owned by the authors, published by EDP Sciences, 2016 Quantum Optics Properties of QCD Vacuum V. Kuvshinov1,a, V. Shaparau1,b, E. Bagashov1,c 1Joint Institute for Power and Nuclear Research - Sosny National Academy of Science of Belarus PO box 119, 220109 Minsk, BELARUS Abstract. Theoretical justification of the occurrence of multimode squeezed and entan- gled colour states in QCD is given. We show that gluon entangled states which are closely related with corresponding squeezed states can appear by the four-gluon self-interaction. Correlations for the collinear gluons are revealed two groups of the colour correlations which is significant at consider of the quark-antiquark pair productions. It is shown that the interaction of colour quark with the stochastic vacuum of QCD leads to the loss of information on the initial colour state of the particle, which gives a new perspective regarding the confinement of quarks phenomenon. The effect is demonstrated for a single particle and in the multiparticle case is proposed. Quantum characteristics (purity and von Neumann entropy) are used to analyse the pro- cess of interaction. 1 Introduction + Many experiments at e e−, pp¯, ep colliders are devoted to hadronic jet physics, since detailed studies of jets are important for better understanding and testing both perturbative and non-perturbative QCD and also for finding manifestations of new physics. Although the nature of jets is of a universal + character, e e−- annihilation stands out among hard processes, since jet events admit a straightforward and clear-cut separation in this process.
    [Show full text]
  • Marc Scott Four Forces of Nature How Strong Is the Strong Force? the Vacuum Isn't Empty Understanding the QCD Vacuum Holography
    TheThe StrangeStrange WorldWorld ofof thethe Marc Scott StrongStrong ForceForce STAG Research Centre & Physics and Astronomy UnderstandingUnderstanding whywhy thethe vacuumvacuum isn'tisn't soso emptyempty Su(ervisor: Prof. Nick Evans AA goodgood wayway toto trytry andand understandunderstand thethe QCDQCD vacuumvacuum isis toto simplifysimplify thethe FourFour forcesforces ofof naturenature UnderstandingUnderstanding situationsituation toto aa twotwo quarkquark QCD,QCD, i.e.i.e. thethe twotwo lightestlightest -- upup (u)(u) andand downdown (d).(d). SinceSince thethe vacuumvacuum inin QCDQCD isis aa seethingseething realmrealm ofof quark-anti-quarkquark-anti-quark (( )) Im%!e- /.01NASA time thethe QCDQCD vacuumvacuum pairspairs –– withwith onlyonly twotwo quarksquarks toto choosechoose fromfrom (u(u oror d),d), therethere areare onlyonly 44 BIG combinationscombinations toto pick;pick; BANG GRAVITYGRAVITY Orbits. Downhill Movement. Bin in! o" #$%r&s insi e n$'leons. EachEach ofof thethe fourfour possiblepossible combinationscombinations hashas aa certaincertain probabilityprobability givengiven byby thethe vacuum,vacuum, Bin in! o" n$'lei. whichwhich variesvaries inin space.space. WeWe cancan representrepresent thisthis onon 4-dimensional4-dimensional grid,grid, eacheach axisaxis beingbeing aa Were all the N$'le%r (ower. forces of nature STRONGSTRONG combination.combination. EachEach locationlocation inin spacespace isis givengiven anan arrowarrow whichwhich isis placedplaced inin thethe 4-D4-D grid,grid, united at the thethe moremore thethe arrowarrow pointspoints inin thethe directiondirection ofof aa givengiven combinationcombination thethe moremore probableprobable beginning of the itit isis (see(see diagram).diagram). universe? Bet% De'%). In fact the vacuum is a little more WEAKWEAK The usual method for analysing interacting systems is constrained. In order to obtain the lowest TheThe usualusual methodmethod forfor analysinganalysing interactinginteracting systemssystems isis perturbation theory, but this relies on the strength of M%!netism.
    [Show full text]
  • Several Effects Unexplained by QCD
    universe Article Several Effects Unexplained by QCD Igor M. Dremin 1,2 1 Lebedev Physics Institute, Moscow 119991, Russia; [email protected] 2 National Research Nuclear University MEPhI, Moscow 115409, Russia Received: 13 March 2018; Accepted: 10 May 2018; Published: 16 May 2018 Abstract: Several new experimental discoveries in high energy proton interactions, yet unexplained by QCD, are discussed in the paper. The increase of the cross sections with increasing energy from ISR to LHC, the correlation between it and the behavior of the slope of the elastic diffraction cone, the unexpected increase of the survival probability of protons in the same energy range, the new structure of the elastic differential cross section at rather large transferred momenta (small distances) and the peculiar ridge effect in high multiplicity inelastic processes are still waiting for QCD interpretation and deeper insight in vacuum. Keywords: proton; quark; gluon; QCD; vacuum; cross section PACS: 13.75 Cs; 13.85 Dz 1. Introduction Cosmic-ray studies revealed many new unexpected features of particle interactions. The invention of particle accelerators and, later on, colliders helped to learn paticle properties in more detail. Nowadays higher energy results come out from the Large Hadron Collider (LHC). Proton beams collide there with energy ps up to 13 TeV in the center-of-mass system that exceeds their own rest mass by more than 4 orders of magnitude. The main goal of the particle studies (and, in particular, those at LHC) is to understand the forces governing the particle interactions and the internal structure of the fundamental blocks of matter1.
    [Show full text]
  • Quantum Vacuum Structure and Cosmology
    Quantum Vacuum Structure and Cosmology Johann Rafelski, Lance Labun, Yaron Hadad, Departments of Physics and Mathematics, The University of Arizona 85721 Tucson, AZ, USA, and Department f¨ur Physik, Ludwig-Maximillians-Universit¨at M¨unchen Am Coulombwall 1, 85748 Garching, Germany Pisin Chen, Leung Center for Cosmology and Particle Astrophysics and Graduate Institute of Astrophysics and Department of Physics, National Taiwan University, Taipei, Taiwan 10617, and Kavli Institute for Particle Astrophysics and Cosmology, SLAC National Accelerator Laboratory, Stanford University, Stanford, CA 94305, U.S.A. Introductory Remarks Contemporary physics faces three great riddles that lie at the intersection of quantum theory, particle physics and cosmology. They are 1. The expansion of the universe is accelerating – an extra factor of two appears in the size. 2. Zero-point fluctuations do not gravitate – a matter of 120 orders of magnitude 3. The “True” quantum vacuum state does not gravitate. The latter two are explicitly problems related to the interpretation and the physi- cal role and relation of the quantum vacuum with and in general relativity. Their resolution may require a major advance in our formulation and understanding of a common unified approach to quantum physics and gravity. To achieve this goal we must develop an experimental basis and much of the discussion we present is devoted to this task. In the following, we examine the observations and the theory contributing to the current framework comprising these riddles. We consider an interpretation of the first riddle within the context of the universe’s quantum vacuum state, and propose an experimental concept to probe the vacuum state of the universe.
    [Show full text]
  • On the Semiclassical Structure of QCD — a Lattice Study at Finite Temperature
    Humboldt-UniversitatÄ zu Berlin Mathematisch-Naturwissenschaftliche FakultatÄ I Institut furÄ Physik On the semiclassical structure of QCD | A lattice study at ¯nite temperature | Diplomarbeit eingereicht von Dirk Peschka geboren am 21. November 1977 in Zossen Aufgabensteller: Prof. Dr. M. Muller-Preu¼kÄ er Zweitgutachter: Prof. Dr. U. Wol® Abgabedatum: 30. August 2004 Contents 1 Introduction 2 2 Quantum mechanics and the semiclassical approximation 5 2.1 The path-integral in quantum mechanics . 5 2.2 Semiclassical approach to quantum mechanics . 8 2.3 Kink solutions and fluctuations . 10 2.4 Kink-gas approximation . 13 2.5 Numerical results for the double-well . 14 2.6 Lessons for QCD . 20 3 Classical SU(3) gauge ¯elds 21 3.1 Classical SU(3) gauge theory . 21 3.2 Calorons in SU(2) . 24 3.3 Calorons in SU(3) . 27 3.4 Instanton model . 29 4 QCD on the lattice 33 4.1 Functional integral for lattice QCD . 33 4.2 QCD at ¯nite temperature . 34 4.3 Improved actions . 37 4.4 Cooling methods . 38 4.5 Detecting classical ¯elds on the lattice . 39 5 Classical solutions on the lattice - examples 42 5.1 Systematics of the investigation . 42 5.2 Constructed calorons with Q = 1 . 45 j j 5.3 Cooled calorons with Q = 1 . 53 j j 5.4 Cooled calorons with Q = 2 . 61 j j 5.5 Caloron-anticaloron superposition with Q = 0 . 67 5.6 Fitting an analytical expression . 70 5.7 Summary . 73 6 Classical solutions on the lattice - statistical properties 74 6.1 Problems ¯nding calorons in SU(3) .
    [Show full text]
  • The Quantum Vacuum and the Cosmological Constant Problem
    The Quantum Vacuum and the Cosmological Constant Problem S.E. Rugh∗and H. Zinkernagely To appear in Studies in History and Philosophy of Modern Physics Abstract - The cosmological constant problem arises at the intersection be- tween general relativity and quantum field theory, and is regarded as a fun- damental problem in modern physics. In this paper we describe the historical and conceptual origin of the cosmological constant problem which is intimately connected to the vacuum concept in quantum field theory. We critically dis- cuss how the problem rests on the notion of physically real vacuum energy, and which relations between general relativity and quantum field theory are assumed in order to make the problem well-defined. 1. Introduction Is empty space really empty? In the quantum field theories (QFT’s) which underlie modern particle physics, the notion of empty space has been replaced with that of a vacuum state, defined to be the ground (lowest energy density) state of a collection of quantum fields. A peculiar and truly quantum mechanical feature of the quantum fields is that they exhibit zero-point fluctuations everywhere in space, even in regions which are otherwise ‘empty’ (i.e. devoid of matter and radiation). These zero-point fluctuations of the quantum fields, as well as other ‘vacuum phenomena’ of quantum field theory, give rise to an enormous vacuum energy density ρvac. As we shall see, this vacuum energy density is believed to act as a contribution to the cosmological constant Λ appearing in Einstein’s field equations from 1917, 1 8πG R g R Λg = T (1) µν − 2 µν − µν c4 µν where Rµν and R refer to the curvature of spacetime, gµν is the metric, Tµν the energy-momentum tensor, G the gravitational constant, and c the speed of light.
    [Show full text]
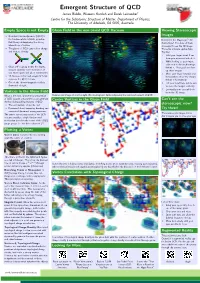
  • Emergent Structure Of
    Emergent Structure of QCD James Biddle, Waseem Kamleh and Derek Leinwebery Centre for the Subatomic Structure of Matter, Department of Physics, The University of Adelaide, SA 5005, Australia Empty Space is not Empty Gluon Field in the non-trivial QCD Vacuum Viewing Stereoscopic Images Quantum Chromodynamics (QCD) is the fundamental relativistic quantum Remember the Magic Eye R 3D field theory underpinning the strong illustrations? You stare at them interactions of nature. cross-eyed to see the 3D image. The gluons of QCD carry colour charge The same principle applies here. and interact directly Try this! 1. Hold your finger about 5 cm from your nose and look at it. 2. While looking at your finger, take note of the double image Gluon self-coupling makes the empty behind it. Your goal is to line vacuum unstable to the formation of up those images. non-trivial quark and gluon condensates. 3. Move your finger forwards and 16 chromo-electric and -magnetic fields backwards to move the images compose the QCD vacuum. behind it horizontally. One of the chromo-magnetic fields is 4. Tilt your head from side to side illustrated at right. to move the images vertically. 5. Eventually your eyes will lock Vortices in the Gluon Field in on the 3D image. What is the most fundamental perspective Stereoscopic image of one the eight chromo-magnetic fields composing the nontrivial vacuum of QCD. of QCD vacuum structure that can generate Centre Vortices in the Gluon Field Can't see the the key distinguishing features of QCD stereoscopic view? The confinement of quarks, and Dynamical chiral symmetry breaking and Try these! associated dynamical-mass generation.
    [Show full text]
  • Chiral Polarization Scale of QCD Vacuum and Spontaneous Chiral Symmetry Breaking Andrei Alexandru George Washington University
    University of Kentucky UKnowledge Anesthesiology Faculty Publications Anesthesiology 2013 Chiral Polarization Scale of QCD Vacuum and Spontaneous Chiral Symmetry Breaking Andrei Alexandru George Washington University Ivan Horváth University of Kentucky, [email protected] Right click to open a feedback form in a new tab to let us know how this document benefits oy u. Follow this and additional works at: https://uknowledge.uky.edu/anesthesiology_facpub Part of the Anesthesiology Commons Repository Citation Alexandru, Andrei and Horváth, Ivan, "Chiral Polarization Scale of QCD Vacuum and Spontaneous Chiral Symmetry Breaking" (2013). Anesthesiology Faculty Publications. 2. https://uknowledge.uky.edu/anesthesiology_facpub/2 This Article is brought to you for free and open access by the Anesthesiology at UKnowledge. It has been accepted for inclusion in Anesthesiology Faculty Publications by an authorized administrator of UKnowledge. For more information, please contact [email protected]. Chiral Polarization Scale of QCD Vacuum and Spontaneous Chiral Symmetry Breaking Notes/Citation Information Published in Journal of Physics: Conference Series, v. 432, conference.1, 012034. The am terial featured on this website is subject to IOP copyright protection, unless otherwise indicated. Digital Object Identifier (DOI) http://dx.doi.org/10.1088/1742-6596/432/1/012034 This article is available at UKnowledge: https://uknowledge.uky.edu/anesthesiology_facpub/2 Home Search Collections Journals About Contact us My IOPscience Chiral polarization scale of QCD vacuum and spontaneous chiral symmetry breaking This content has been downloaded from IOPscience. Please scroll down to see the full text. 2013 J. Phys.: Conf. Ser. 432 012034 (http://iopscience.iop.org/1742-6596/432/1/012034) View the table of contents for this issue, or go to the journal homepage for more Download details: IP Address: 72.5.9.197 This content was downloaded on 29/10/2014 at 21:28 Please note that terms and conditions apply.
    [Show full text]