Calcium Movement in the Sarcomere and Its Connection To
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Passive Tension in Cardiac Muscle: Contribution of Collagen, Titin, Microtubules, and Intermediate Filaments
Biophysical Journal Volume 68 March 1995 1027-1044 1027 Passive Tension in Cardiac Muscle: Contribution of Collagen, Titin, Microtubules, and Intermediate Filaments Henk L. Granzier and Thomas C. Irving Department of Veterinary and Comparative Anatomy, Pharmacology, and Physiology, Washington State University, Pullman, Washington 99164·6520 USA ABSTRACT The passive tension-sarcomere length relation of rat cardiac muscle was investigated by studying passive (or not activated) single myocytes and trabeculae. The contribution ofcollagen, titin, microtubules, and intermediate filaments to tension and stiffness was investigated by measuring (1) the effects of KCI/KI extraction on both trabeculae and single myocytes, (2) the effect of trypsin digestion on single myocytes, and (3) the effect of colchicine on single myocytes. It was found that over the working range of sarcomeres in the heart (lengths -1.9-2.2 11m), collagen and titin are the most important contributors to passive tension with titin dominating at the shorter end of the working range and collagen at longer lengths. Microtubules made a modest contribution to passive tension in some cells, but on average their contribution was not significant. Finally, intermediate filaments contribl,!ted about 10%to passive tension oftrabeculae at sarcomere lengths from -1.9to 2.1 11m, and theircontribution dropped to only a few percent at longer lengths. At physiological sarcomere lengths of the heart, cardiac titin developed much higher tensions (>20-fold) than did skeletal muscle titin at comparable lengths. This might be related to the finding that cardiac titin has a molecular mass of 2.5 MDa, 0.3-0.5 MDa smaller than titin of mammalian skeletal muscle, which is predicted to result in a much shorter extensible titin segment in the I-band of cardiac muscle. -

Back-To-Basics: the Intricacies of Muscle Contraction
Back-to- MIOTA Basics: The CONFERENCE OCTOBER 11, Intricacies 2019 CHERI RAMIREZ, MS, of Muscle OTRL Contraction OBJECTIVES: 1.Review the anatomical structure of a skeletal muscle. 2.Review and understand the process and relationship between skeletal muscle contraction with the vital components of the nervous system, endocrine system, and skeletal system. 3.Review the basic similarities and differences between skeletal muscle tissue, smooth muscle tissue, and cardiac muscle tissue. 4.Review the names, locations, origins, and insertions of the skeletal muscles found in the human body. 5.Apply the information learned to enhance clinical practice and understanding of the intricacies and complexity of the skeletal muscle system. 6.Apply the information learned to further educate clients on the importance of skeletal muscle movement, posture, and coordination in the process of rehabilitation, healing, and functional return. 1. Epithelial Four Basic Tissue Categories 2. Muscle 3. Nervous 4. Connective A. Loose Connective B. Bone C. Cartilage D. Blood Introduction There are 3 types of muscle tissue in the muscular system: . Skeletal muscle: Attached to bones of skeleton. Voluntary. Striated. Tubular shape. Cardiac muscle: Makes up most of the wall of the heart. Involuntary. Striated with intercalated discs. Branched shape. Smooth muscle: Found in walls of internal organs and walls of vascular system. Involuntary. Non-striated. Spindle shape. 4 Structure of a Skeletal Muscle Skeletal Muscles: Skeletal muscles are composed of: • Skeletal muscle tissue • Nervous tissue • Blood • Connective tissues 5 Connective Tissue Coverings Connective tissue coverings over skeletal muscles: .Fascia .Tendons .Aponeuroses 6 Fascia: Definition: Layers of dense connective tissue that separates muscle from adjacent muscles, by surrounding each muscle belly. -
THE MUSCLE SPINDLE Anatomical Structures of the Spindle Apparatus
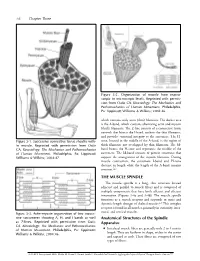
56 Chapter Three Figure 3-2. Organization of muscle from macro- scopic to microscopic levels. Reprinted with permis- sion from Oatis CA. Kinesiology: The Mechanics and Pathomechanics of Human Movement. Philadelphia, Pa: Lippincott Williams & Wilkins; 2004:46. which contains only actin (thin) filaments. The darker area is the A-band, which contains alternating actin and myosin (thick) filaments. The Z-line consists of a connective tissue network that bisects the I-band, anchors the thin filaments, and provides structural integrity to the sarcomere. The H- Figure 3-1. Successive connective tissue sheaths with- zone, located in the middle of the A-band, is the region of in muscle. Reprinted with permission from Oatis thick filaments not overlapped by thin filaments. The M- CA. Kinesiology: The Mechanics and Pathomechanics band bisects the H-zone and represents the middle of the of Human Movement. Philadelphia, Pa: Lippincott sarcomere. The M-band consists of protein structures that Williams & Wilkins; 2004:47. support the arrangement of the myosin filaments. During muscle contraction, the sarcomere I-band and H-zone decrease in length while the length of the A-band remains constant.2,3 THE MUSCLE SPINDLE The muscle spindle is a long, thin structure located adjacent and parallel to muscle fibers and is composed of multiple components that have both afferent and efferent innervation (Figures 3-4a and 3-4b). The muscle spindle functions as a stretch receptor and responds to static and dynamic length changes of skeletal muscle.4-6 This complex receptor is found in all muscles, primarily in extremity, inter- costal, and cervical muscles. -

Muscle Physiology Dr
Muscle Physiology Dr. Ebneshahidi Copyright © 2004 Pearson Education, Inc., publishing as Benjamin Cummings Skeletal Muscle Figure 9.2 (a) Copyright © 2004 Pearson Education, Inc., publishing as Benjamin Cummings Functions of the muscular system . 1. Locomotion . 2. Vasoconstriction and vasodilatation- constriction and dilation of blood vessel Walls are the results of smooth muscle contraction. 3. Peristalsis – wavelike motion along the digestive tract is produced by the Smooth muscle. 4. Cardiac motion . 5. Posture maintenance- contraction of skeletal muscles maintains body posture and muscle tone. 6. Heat generation – about 75% of ATP energy used in muscle contraction is released as heat. Copyright. © 2004 Pearson Education, Inc., publishing as Benjamin Cummings . Striation: only present in skeletal and cardiac muscles. Absent in smooth muscle. Nucleus: smooth and cardiac muscles are uninculcated (one nucleus per cell), skeletal muscle is multinucleated (several nuclei per cell ). Transverse tubule ( T tubule ): well developed in skeletal and cardiac muscles to transport calcium. Absent in smooth muscle. Intercalated disk: specialized intercellular junction that only occurs in cardiac muscle. Control: skeletal muscle is always under voluntary control‚ with some exceptions ( the tongue and pili arrector muscles in the dermis). smooth and cardiac muscles are under involuntary control. Copyright © 2004 Pearson Education, Inc., publishing as Benjamin Cummings Innervation: motor unit . a) a motor nerve and a myofibril from a neuromuscular junction where gap (called synapse) occurs between the two structures. at the end of motor nerve‚ neurotransmitter (i.e. acetylcholine) is stored in synaptic vesicles which will release the neurotransmitter using exocytosis upon the stimulation of a nerve impulse. Across the synapse the surface the of myofibril contains receptors that can bind with the neurotransmitter. -

Massive Alterations of Sarcoplasmic Reticulum Free Calcium in Skeletal Muscle Fibers Lacking Calsequestrin Revealed by a Genetic
Massive alterations of sarcoplasmic reticulum free calcium in skeletal muscle fibers lacking calsequestrin revealed by a genetically encoded probe M. Canatoa,1, M. Scorzetoa,1, M. Giacomellob, F. Protasic,d, C. Reggiania,d, and G. J. M. Stienene,2 Departments of aHuman Anatomy and Physiology and bExperimental Veterinary Sciences, University of Padua, 35121 Padua, Italy; cCeSI, Department of Basic and Applied Medical Sciences, University G. d’Annunzio, I-66013 Chieti, Italy; dIIM-Interuniversity Institute of Myology and eLaboratory for Physiology, Institute for Cardiovascular Research, VU University Medical Center, 1081BT, Amsterdam, The Netherlands Edited* by Clara Franzini-Armstrong, University of Pennsylvania Medical Center, Philadelphia, PA, and approved November 12, 2010 (received for review June 30, 2010) The cytosolic free Ca2+ transients elicited by muscle fiber excitation tion essential to maintain a low metabolic rate in quiescent ex- are well characterized, but little is known about the free [Ca2+] citable cells. In addition, CSQ has been shown to modulate RyR- dynamics within the sarcoplasmic reticulum (SR). A targetable mediated Ca2+ release from the SR (6). To understand the pivotal ratiometric FRET-based calcium indicator (D1ER Cameleon) allowed role of CSQ in SR function, it is critical to determine free SR us to investigate SR Ca2+ dynamics and analyze the impact of cal- Ca2+ concentration, and this has been made possible by the ad- sequestrin (CSQ) on SR [Ca2+] in enzymatically dissociated flexor vent of a targetable ratiometric FRET-based indicator, such as digitorum brevis muscle fibers from WT and CSQ-KO mice lacking D1ER Cameleon (7). Seminal studies using this technique have isoform 1 (CSQ-KO) or both isoforms [CSQ-double KO (DKO)]. -

Localization of Ca2l Release Channels with Ryanodine in Junctional
Proc. NatI. Acad. Sci. USA Vol. 82, pp. 7256-7259, November 1985 Biochemistry Localization of Ca2l release channels with ryanodine in junctional terminal cisternae of sarcoplasmic reticulum of fast skeletal muscle (muscle contraction/excitation-contraction coupling/ruthenium red/longitudinal cisternae/gated channels) SIDNEY FLEISCHER, EUNICE M. OGUNBUNMI, MARK C. DIXON, AND EDUARD A. M. FLEER Department of Molecular Biology, Vanderbilt University, Nashville, TN 37235 Communicated by William J. Darby, July 8, 198S ABSTRACT The mechanism of Ca2' release from tional terminal cisternae consist of two types of membranes, sarcoplasmic reticulum, which triggers contraction in skeletal the Ca2l pump membrane (80-85%) and the junctional face muscle, remains the key unresolved problem in excita- membrane (15-20%) (16). A unique characteristic of junc- tion-contraction coupling. Recently, we have described the tional terminal cisternae is that they have a poor Ca2+ loading isolation of purified fractions referable to terminal and longi- rate, which can be enhanced 5-fold or more by addition of tudinal cisternae of sarcoplasmic reticulum. Junctional termi- ruthenium red (RR) (ref. 17; unpublished data). This study nal cisternae are distinct in that they have a low net energized describes the drug action of ryanodine on the junctional Ca2+ loading, which can be enhanced 5-fold or more by terminal cisternae in blocking the action of RR. It provides addition of ruthenium red. The loading rate, normalized for evidence that the action of ryanodine is on the Ca2' release calcium pump protein content, then approaches that of longi- mechanism and supports the view that Ca2' release is tudinal cisternae of sarcoplasmic reticulum. -

Uniform Sarcomere Shortening Behavior in Isolated Cardiac Muscle Cells
Uniform Sarcomere Shortening Behavior in Isolated Cardiac Muscle Cells JOHN W. KRUEGER, DAMIAN FORLETTI, and BEATRICE A. WITTENBERG From the Albert Einstein College of Medicine, Departments of Medicine and Physiology, Bronx, New York 10461 ABSTRACT We have observed the dynamics of sarcomere shortening and the diffracting action of single, functionally intact, unattached cardiac muscle cells enzymatically isolated from the ventricular tissue of adult rats. Sarcomere length was measured either (a) continuously by a light diffraction method or (b) by direct inspection of the cell's striated image as recorded on videotape or by cinemicroscopy (120-400 frames/s). At physiological levels of added CaCl2 (0.5- 2.0 mM), many cells were quiescent (i.e., they did not beat spontaneously) and contracted in response to electrical stimulation (~ 1.0-ms pulse width). Sarcomere length in the quiescent, unstimulated cells (1.93 + 0.10 [SD] /~m), at peak shortening (1.57 + 0.13/~m, n = 49), and the maximum velocity of sarcomere shortening and relengthening were comparable to previous observations in intact heart muscle preparations. The dispersion of light diffracted by the cell remained narrow, and individual striations remained distinct and laterally well registered throughout the shortening-relengthening cycle. In contrast, apprecia- ble nonuniformity and internal buckling were seen at sarcomere lengths < 1.8 /~m when the resting cell, embedded in gelatin, was longitudinally compressed. These results indicate (a) that shortening and relengthening is characterized by uniform activation between myofibrils within the cardiac cell and (b) that physiologically significant relengthening forces in living heart muscle originate at the level of the cell rather than in extracellular connections. -

Ultra-High Resolution Scanning Electron Microscopic Studies on the Sarcoplasmic Reticulum and Mitochondria in Various Muscles: a Review
Scanning Microscopy Volume 7 Number 1 Article 16 12-29-1992 Ultra-High Resolution Scanning Electron Microscopic Studies on the Sarcoplasmic Reticulum and Mitochondria in Various Muscles: A Review Takuro Ogata Kochi Medical School Yuichi Yamasaki Kochi Medical School Follow this and additional works at: https://digitalcommons.usu.edu/microscopy Part of the Biology Commons Recommended Citation Ogata, Takuro and Yamasaki, Yuichi (1992) "Ultra-High Resolution Scanning Electron Microscopic Studies on the Sarcoplasmic Reticulum and Mitochondria in Various Muscles: A Review," Scanning Microscopy: Vol. 7 : No. 1 , Article 16. Available at: https://digitalcommons.usu.edu/microscopy/vol7/iss1/16 This Article is brought to you for free and open access by the Western Dairy Center at DigitalCommons@USU. It has been accepted for inclusion in Scanning Microscopy by an authorized administrator of DigitalCommons@USU. For more information, please contact [email protected]. Scanning Microscopy, Vol. 7, No. 1, 1993 (Pages 145-156) 0891-7035/93$5 .00+ .00 Scanning Microscopy International, Chicago (AMF O'Hare), IL 60666 USA ULTRA-HIGH RESOLUTION SCANNING ELECTRON MICROSCOPIC STUDIES ON THE SARCOPLASMIC RETICULUM AND MITOCHONDRIA IN VARIOUS MUSCLES: A REVIEW Takuro Ogata* and Yuichi Yamasaki Department of Surgery, Kochi Medical School Nankoku, Kochi, 783 Japan (Received for publication March 23, 1992, and in revised form December 29, 1992) Abstract Introduction The three-dimensional structure of the sarco The three-dimensional models of the membrane plasm.ic -

Titin N2A Domain and Its Interactions at the Sarcomere
International Journal of Molecular Sciences Review Titin N2A Domain and Its Interactions at the Sarcomere Adeleye O. Adewale and Young-Hoon Ahn * Department of Chemistry, Wayne State University, Detroit, MI 48202, USA; [email protected] * Correspondence: [email protected]; Tel.: +1-(313)-577-1384 Abstract: Titin is a giant protein in the sarcomere that plays an essential role in muscle contraction with actin and myosin filaments. However, its utility goes beyond mechanical functions, extending to versatile and complex roles in sarcomere organization and maintenance, passive force, mechanosens- ing, and signaling. Titin’s multiple functions are in part attributed to its large size and modular structures that interact with a myriad of protein partners. Among titin’s domains, the N2A element is one of titin’s unique segments that contributes to titin’s functions in compliance, contraction, structural stability, and signaling via protein–protein interactions with actin filament, chaperones, stress-sensing proteins, and proteases. Considering the significance of N2A, this review highlights structural conformations of N2A, its predisposition for protein–protein interactions, and its multiple interacting protein partners that allow the modulation of titin’s biological effects. Lastly, the nature of N2A for interactions with chaperones and proteases is included, presenting it as an important node that impacts titin’s structural and functional integrity. Keywords: titin; N2A domain; protein–protein interaction 1. Introduction Citation: Adewale, A.O.; Ahn, Y.-H. The complexity of striated muscle is defined by the intricate organization of its com- Titin N2A Domain and Its ponents [1]. The involuntary cardiac and voluntary skeletal muscles are the primary types Interactions at the Sarcomere. -

Effect of Camkiiδ Deletion on Sarcomere Structure
Features Efect of CaMKIIδ Deletion on Sarcomere Structure Tik-Chee (Jenny) Cheng, Sukriti Dewan, Andrew McCulloch, Jef Omens Jenny Cheng is a senior at Earl Warren College majoring in Bioengineering with a focus in Biotechnology. In Fall 2015, she will be pursuing her PhD in Biomedical Engineering at the University of Wisconsin-Madison, studying cardiovascular pathophysiology for clinical applications. Heart failure, a progressive cardiomyopathy, a condition with condition that is typically enlarged left ventricles and/or undetected and often dilated ventricular walls that can misdiagnosed, is the leading lead to dysfunction and inadequate cause of deaths around pumping of blood to the rest of the world. The disorder is the body. Calcium/calmodulin- CaMKII isoform (CaMKIIδ) characterized by the inability dependent protein kinase II appear to be protected of the heart to keep up with (CaMKII) is a protein kinase from such dysfunction and the body’s demand for blood that can phosphorylate many hypertrophy. circulation. It is initiated substrates and regulates a wide by structural and functional range of cellular function. Its role Normal myocardial function changes from in calcium signaling is dependent on the structure The disorder is molecular to pathways has been of cardiomyocytes, specifcally systemic levels characterized by implicated in the the basic subunits of muscle that result in the inability of the pathophysiology called sarcomeres. Sarcomeres compensatory cardiac pump to of adverse cardiac contract and generate force physiological keep up with the left ventricular by utilizing the motor changes, body’s demand. remodeling. movements of thin and thick commonly Animal models flaments, specifcally myosin termed cardiac remodeling. -

Defects in T-Tubular Electrical Activity Underlie Local Alterations of Calcium Release in Heart Failure
Defects in T-tubular electrical activity underlie local alterations of calcium release in heart failure Claudia Crocinia, Raffaele Coppinib, Cecilia Ferrantinic, Ping Yand, Leslie M. Loewd, Chiara Tesic, Elisabetta Cerbaib, Corrado Poggesic, Francesco S. Pavonea,e,f, and Leonardo Sacconia,f,1 aEuropean Laboratory for Non-Linear Spectroscopy, 50019 Florence, Italy; bDivision of Pharmacology, Department “NeuroFarBa,” University of Florence, 50139 Florence, Italy; cDivision of Physiology, Department of Experimental and Clinical Medicine, University of Florence, 50134 Florence, Italy; dR. D. Berlin Center for Cell Analysis and Modeling, University of Connecticut Health Center, Farmington, CT 06030; eDepartment of Physics and Astronomy, University of Florence, 50019 Sesto Fiorentino, Italy; and fNational Institute of Optics, National Research Council, 50125 Florence, Italy Edited by Clara Franzini-Armstrong, University of Pennsylvania Medical Center, Philadelphia, PA, and approved September 15, 2014 (received for review June 20, 2014) Action potentials (APs), via the transverse axial tubular system in a rat model of postischemic HF, structurally remodeled TATS + (TATS), synchronously trigger uniform Ca2 release throughout the exhibits abnormal electrical activity, i.e., failure of AP propagation cardiomyocyte. In heart failure (HF), TATS structural remodeling and presence of local spontaneous depolarizations. Tubular AP occurs, leading to asynchronous Ca2+ release across the myocyte failures and spontaneous activity can potentially aggravate asyn- + and contributing to contractile dysfunction. In cardiomyocytes from chronous Ca2 release and determine nonhomogeneous myofibril + failing rat hearts, we previously documented the presence of TATS contraction. Simultaneous recording of local Ca2 release and AP in elements which failed to propagate AP and displayed spontaneous the tubular network is needed to unravel the consequences of these + + electrical activity; the consequence for Ca2 release remained, how- electrical anomalies on intracellular Ca2 dynamics. -

Muscular System ANS 215 Physiology and Anatomy of Domesticated Animals
Muscular System ANS 215 Physiology and Anatomy of Domesticated Animals I. Skeletal Muscle Contraction A. Neuromuscular junction functions as an amplifier for a nerve impulse B. Arrival of a spinal or cranial nerve impulse at the neuromuscular junction results in release of acetylcholine (Ach) into the space between the nerve fiber terminal branch and the muscle fiber C. Release of Ach is accelerated because Ca ions from extracellular fluid enter the prejunctional membrane when the nerve impulse arrives D. Ach is the stimulus that increases the permeability of the muscle fiber membrane for Na ions, after which depolarization begins E. Depolarization proceeds in all directions from the neuromuscular junction F. Impulse is conducted into all parts of the muscle fiber by the sarcotubular system (synchronizes muscle fiber contraction) G. Low concentration of Ca in the extracellular fluid is recognized clinically in dairy cows after calving (parturient paresis) as a state of semi-paralysis caused by partial neuromuscular block. H. Almost immediately after its release Ach is hydrolyzed by the enzyme acetylcholinesterase into acetic acid and choline I. Next depolarization must await the arrival of the next nerve impulse J. Tubules of sarcoplasmic reticulum have a relatively high concentration of Ca ions K. Depolarization of these tubules results in a simultaneous release of Ca ions into the sarcoplasm, which in turn diffuse rapidly into the myofibrils L. Presence of Ca ions within the myofibrils initiates the contraction process M. The Ca ions are returned rapidly by active transport to the sarcoplasmic reticulum after contraction is initiated and are released again when the next signal arrives.