Basketball Background 7 3.1
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Ponuda Za LIVE 30.12.2017
powered by BetO2 kickoff_time event_id sport competition_name home_name away_name 2017-12-30 09:00:00 1050635 BASKETBALL South Korea KBL KCC Egis Seoul Thunders 2017-12-30 09:00:00 1050636 BASKETBALL South Korea WKBL Woori Bank Hansae Women Bucheon Keb Hanabank Women 2017-12-30 09:30:00 1050637 BASKETBALL Australia WNBL Women Melbourne Boomers Women Dandenong Women 2017-12-30 11:00:00 1050638 BASKETBALL Turkey Super Ligi Sakarya Pinar Karsiyaka 2017-12-30 11:30:00 1050733 BASKETBALL Turkey TBL Bahcesehir Koleji Socar Petkimspor 2017-12-30 12:30:00 1050639 BASKETBALL China WCBA Bayi Women Xinjiang Women 2017-12-30 12:30:00 1050640 BASKETBALL China WCBA Guangdong Women Jiangsu Women 2017-12-30 12:30:00 1050641 BASKETBALL China WCBA Liaoning Women Beijing Women 2017-12-30 12:30:00 1050642 BASKETBALL China WCBA Shenyang Women Zhejiang Women 2017-12-30 12:30:00 1050643 BASKETBALL China WCBA Shandong Women Shanxi Xing Rui Women 2017-12-30 12:30:00 1050644 BASKETBALL China WCBA Shanghai Women Shaanxi Tianze Women 2017-12-30 12:30:00 1050866 BASKETBALL China WCBA Sichuan Women Heilongjiang Women 2017-12-30 12:30:00 1050758 BASKETBALL Turkey TBL Bakirkoy Yalova Belediye 2017-12-30 12:35:00 1050647 BASKETBALL China CBA Sichuan Guangzhou 2017-12-30 12:35:00 1050648 BASKETBALL China CBA Qingdao Beikong 2017-12-30 12:35:00 1050649 BASKETBALL China CBA Zhejiang Chouzhou Bank Jiangsu Dragons 2017-12-30 13:00:00 1050645 BASKETBALL China CBA Xinjiang Shenzhen 2017-12-30 13:15:00 1050650 BASKETBALL Turkey Super Ligi Usak Eskisehir Basket 2017-12-30 14:00:00 -

Similarities and Differences Among Continental Basketball Championships
RICYDE. Revista Internacional de Ciencias del Deporte doi:10.5232/ricyde Rev. int. cienc. deporte RICYDE. Revista Internacional de Ciencias del Deporte VOLUME XIV - YEAR XIV Pages:42-54 ISSN:1 8 8 5 - 3 1 3 7 https://doi.org/10.5232/ricyde2018.05104 Issue: 51 - January - 2018 Basketball without borders? Similarities and differences among Continental Basketball Championships ¿Baloncesto sin fronteras? Similitudes y diferencias entre los Campeonatos Continentales de baloncesto Sergio José Ibáñez1, Sergio González-Espinosa1, Sebastián Feu2 & Javier García-Rubio3 1.Facultad de Ciencias del Deporte. Universidad de Extremadura. Spain 2.Facultad de Ciencias de la Educación. Universidad de Extremadura. Spain 3.Facultad de Educación. Universidad Autónoma de Chile. Chile Abstract The analysis of technical-tactical performance indicators is an excellent tool for coaches, because it provides objective informa- tion on the actions of players and teams. The aim of this investigation was to study the performance indicators for the last con- tinental basketball championships. Five continental championships played in 2015 were analysed for a total of 213 matches. The variables analysed were: ball possessions, point difference, points scored, one, two and three point throws attempted and sco- red, total and defensive and offensive rebounds, assists, steals, turnovers, blocks for and against, fouls committed and received, and evaluation. A descriptive analysis and performance profiles were carried out to characterise the sample. A one-way ANOVA and Bonferroni correction were used to identify the differences among championships. A discriminant analysis was performed to identify the performance indicators best characterising each analysed championship. The results show that there are differences among all the championships and all the performance indicators, except in three point throws scored and blocks. -
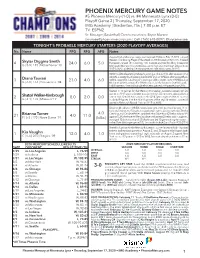
PHOENIX MERCURY GAME NOTES #5 Phoenix Mercury (1-0) Vs
PHOENIX MERCURY GAME NOTES #5 Phoenix Mercury (1-0) vs. #4 Minnesota Lynx (0-0) Playoff Game 2 | Thursday, September 17, 2020 IMG Academy | Bradenton, Fla. | 7:00 p.m. ET TV: ESPN2 Sr. Manager, Basketball Communications: Bryce Marsee [email protected] | Cell: (765) 618-0897 | @brycemarsee TONIGHT'S PROBABLE MERCURY STARTERS (2020 PLAYOFF AVERAGES) No. Name PPG RPG APG Notes Aquired by the Mercury in a sign-and-trade with Dallas on Feb. 12, 2020...named Western Conference Player of the Week on 9/8 for week of 8/31-9/6...finished 4 Skylar Diggins-Smith 24.0 6.0 5.0 the season ranked 7th in scoring, 10th in assists and tied for 4th in three-point G | 5-9 | 145 | Notre Dame '13 field goals (46)...scored a postseason career-high and team-high 24 points on 9/15 vs. WAS...picked up her first playoffs win over Washington on 9/15 WNBA's all-time leader in postseason scoring and ranks 3rd in all-time assists in the playoffs...6 assists shy of passing Sue Bird for 2nd on WNBA's all-time playoffs as- 3 Diana Taurasi 23.0 4.0 6.0 sists list...ranked 5th in the league in scoring and 8th in assists...led the WNBA in 3-pt G | 6-0 | 163 | Connecticut '04 field goals (61) this season, the 11th time she's led the league in 3-pt field goals... holds a perfect 7-0 record in single elimination games in the playoffs since 2016 Started in 10 games for the Mercury this season..scored a career-high 24 points on 9/11 against Seattle in a career-high 35 mimutes...also posted a 2 Shatori Walker-Kimbrough 8.0 2.0 0.0 career-high 5 steals this season in the 8/14 game against Atlanta...scored G | 6-1 | 170 | Missouri '19 in double figures 5 of the final 8 games of the regular season...scored 8 points in Mercury's Round 1 win on 9/15 vs. -

Quantifying How NBA Playoff Format Impacts Playoff Excitement
Quantifying How NBA Playoff Format Impacts Playoff Excitement Quinn Johnson, Bailey Fosdick, Connor Gibbs Colorado State University, Fort Collins, Colorado, United States Abbreviated abstract: The National Basketball Association has predominantly kept its same basic playoff format since 1984. Here, we explore two alternative playoff formats and quantify the expected excitement in game play across the playoffs. We consider format changes to include each conference's top 8 teams and playing a conference-less tournament, as well as, taking the top 16 teams in the NBA and playing a conference-less tournament. Using simulation, we found small to no differences in excitement between the three formats but continue to endorse the top 16 team system due its advantage in fairness to all teams. Related publications: – Tokarz D. How We Make the YUSAG Power Rankings. R: NBA Power Rankings. 2018 Mar 20. UCSAS [email protected] - 1 2020 Motivation Deserving teams are often left out Would changing the playoff format of postseason due to conference result in a drastically more or less strength differences. exciting postseason? Seeding Differences between Current and Top 16 Format Possible playoff formats Current play: conference who’s in: Top 8 West, Top 8 East –––––––––––––––––––––––––––––––––– 8W8E play: overall seeding who’s in: Top 8 West, Top 8 East –––––––––––––––––––––––––––––––––– 16TOT play: overall seeding who’s in: Top 16 NBA UCSAS 2020 Methods 1) Model win probability for each game 2) Simulate playoffs under different formats • Using -

Article 340 Playoffs #3400. All Playoffs Managed By
ARTICLE 340 PLAYOFFS #3400. ALL PLAYOFFS MANAGED BY COMMISSIONER All playoffs of the CIF Southern Section shall be under the management of the Commissioner of Athletics, who will have final authority and responsibility for their conduct. #3400.1 Enrollment based divisions will be used in the sports of boys and girls cross country and boys and girls track and field. By action of the Southern Section Council, once the divisions are established for the playoff, no school shall be allowed to move up to a larger enrollment division. Schools will participate based upon their CBED enrollment figures. Consideration will be given to geography after league placement has been recognized. #3400.2 No playoffs will be conducted by the CIF Southern Section Office when less than 20% of the membership field teams in that sport. #3400.3 See 54.8 (Emergency Powers). #3401. REPORT OF PLAYOFFS eAt the clos of the season for each sport, the Commissioner of Athletics shall compile a report of the playoffs in the “CIF Southern Section Bulletin.” #3402. IDENTIFYING LEAGUE REPRESENTATIVES INTO THE PLAYOFFS Under the playoff format ‐ in all sports ‐ leagues have the responsibility of developing and identifying the priority for their representatives into the playoffs. This will include the league’s priority with regard to any at‐large consideration. Thus, the league through its CIF Council Representative, MUST notify the CIF Southern Section Office prior to the playoff draw, the No. 1 representative, the No. 2 representative, the No. 3 representative, and the league’s priority team for consideration to any at‐large berth. -

Dallas Mavericks (42-30) (3-3)
DALLAS MAVERICKS (42-30) (3-3) @ LA CLIPPERS (47-25) (3-3) Game #7 • Sunday, June 6, 2021 • 2:30 p.m. CT • STAPLES Center (Los Angeles, CA) • ABC • ESPN 103.3 FM • Univision 1270 THE 2020-21 DALLAS MAVERICKS PLAYOFF GUIDE IS AVAILABLE ONLINE AT MAVS.COM/PLAYOFFGUIDE • FOLLOW @MAVSPR ON TWITTER FOR STATS AND INFO 2020-21 REG. SEASON SCHEDULE PROBABLE STARTERS DATE OPPONENT SCORE RECORD PLAYER / 2020-21 POSTSEASON AVERAGES NOTES 12/23 @ Suns 102-106 L 0-1 12/25 @ Lakers 115-138 L 0-2 #10 Dorian Finney-Smith LAST GAME: 11 points (3-7 3FG, 2-2 FT), 7 rebounds, 4 assists and 2 steals 12/27 @ Clippers 124-73 W 1-2 F • 6-7 • 220 • Florida/USA • 5th Season in 42 minutes in Game 6 vs. LAC (6/4/21). NOTES: Scored a playoff career- 12/30 vs. Hornets 99-118 L 1-3 high 18 points in Game 1 at LAC (5/22/21) ... hit GW 3FG vs. WAS (5/1/21) 1/1 vs. Heat 93-83 W 2-3 GP/GS PPG RPG APG SPG BPG MPG ... DAL was 21-9 during the regular season when he scored in double figures, 1/3 @ Bulls 108-118 L 2-4 6/6 9.0 6.0 2.2 1.3 0.3 38.5 1/4 @ Rockets 113-100 W 3-4 including 3-1 when he scored 20+. 1/7 @ Nuggets 124-117* W 4-4 #6 LAST GAME: 7 points, 5 rebounds, 3 assists, 3 steals and 1 block in 31 1/9 vs. -

Implementing Financial Fair Play Rules at Latvian-Estonian Basketball League
RIČARDS VAMBUTS IMPLEMENTING FINANCIAL FAIR PLAY RULES AT LATVIAN-ESTONIAN BASKETBALL LEAGUE Final Master Thesis Study programme: Sport Business Management State code 6211LX001 Supervisor: Assoc. prof. dr. Renata Legenzova Defended: Assoc. prof., dr. Rita Bendaravičienė Dean of the Faculty of Economics and Management Kaunas, 2021 Table of contents SUMMARY ........................................................................................................................................ 3 INTRODUCTION ............................................................................................................................... 4 I. LITERATURE REVIEW ON FINANCIAL FAIRPLAY AND FINANCIAL STABILITY ......... 6 1.1 The concept of financial stability in sports and its influencing factors ......................................... 6 1.2 Measures of financial stability ....................................................................................................... 8 1.3 Financial fair-play rules and their influence on financial stability in sports ............................... 11 1.4 Overview of financial fair-play rules in practices - cases of Euroleague and NBA .................... 15 II. ANALYSIS OF TEAMS' FINANCIAL STABILITY IN LATVIAN-ESTONIAN LEAGUE AND COMPARATIVE ANALYSIS OF FAIR-PLAY RULES ACROSS THE LEAGUES .......... 23 2.1 Overview of Latvian-Estonian basketball league ........................................................................ 23 2.2 Research methodology ................................................................................................................ -

Effects of Home-Away Sequencing on the Length of Best-Of-Seven Game Playoff Series
Bowling Green State University ScholarWorks@BGSU Applied Statistics and Operations Research Faculty Publications Applied Statistics and Operations Research 2006 Effects of Home-Away Sequencing on the Length of Best-of-Seven Game Playoff Series Christopher M. Rump Bowling Green State University, [email protected] Follow this and additional works at: https://scholarworks.bgsu.edu/asor_pub Part of the Social Statistics Commons Repository Citation Rump, Christopher M., "Effects of Home-Away Sequencing on the Length of Best-of-Seven Game Playoff Series" (2006). Applied Statistics and Operations Research Faculty Publications. 2. https://scholarworks.bgsu.edu/asor_pub/2 This Article is brought to you for free and open access by the Applied Statistics and Operations Research at ScholarWorks@BGSU. It has been accepted for inclusion in Applied Statistics and Operations Research Faculty Publications by an authorized administrator of ScholarWorks@BGSU. Journal of Quantitative Analysis in Sports Volume 2, Issue 1 2006 Article 5 The Effects of Home-Away Sequencing on the Length of Best-of-Seven Game Playoff Series Christopher M. Rump∗ ∗Bowling Green State University, [email protected] Copyright c 2006 The Berkeley Electronic Press. All rights reserved. The Effects of Home-Away Sequencing on the Length of Best-of-Seven Game Playoff Series Christopher M. Rump Abstract We analyze the number of games played in a seven-game playoff series under various home- away sequences. In doing so, we employ a simple Bernoulli model of home-field advantage in which the outcome of each game in the series depends only on whether it is played at home or away with respect to a designated home team. -

Open Patrick Kemp___Final Thesis.Pdf
THE PENNSYLVANIA STATE UNIVERSITY SCHREYER HONORS COLLEGE DEPARTMENT OF ECONOMICS THE ECONOMIC SIGNIFICANCE OF COMPETITIVE BALANCE IN THE NATIONAL BASKETBALL ASSOCIATION: AN EMPIRICAL ANALYSIS OF THE DETERMINANTS OF LOCAL DEMAND PATRICK J KEMP SPRING 2010 A thesis submitted in partial fulfillment of the requirements for a baccalaureate degree in Economics with honors in Economics Reviewed and approved* by the following: Dr. Edward Coulson Professor of Economics Thesis Supervisor Dr. David Shapiro Professor of Economics and Co-Director of Undergraduate Studies Honors Adviser * Signatures are on file in the Schreyer Honors College i Abstract In the study of sports economics the notion of competitive balance is well known. This thesis seeks to expand upon this well known notion and use it as part of an empirical analysis of the determinants of local demand for NBA franchises. This paper starts by focusing on the traditional notion of competitive balance, with specific regard to the sport basketball and the National Basketball Association specifically. It then quantifies the degree of competitive balance in the NBA since 1990 using metrics similar to those used by Quirk and Fort in their 1992 book Pay Dirt: The Business of Professional Team Sports. An extensive amount of linear regression analysis is then conducted, first looking at all teams and then teams belonging to certain market types. The empirical results indicate that competitive balance is not a significant determinant of local demand. The results also indicate key differences in the determinants between low-income market teams and high-income market teams. I make two recommendations as to how the NBA could beneficially alter its business model based upon these regression results: abolishing guaranteed contracts and changing the 100/0 home/away gate split. -

Ponuda Za LIVE 27.12.2017
powered by BetO2 kickoff_time event_id sport competition_name home_name away_name 2017-12-27 09:15:00 1049599 BASKETBALL Philippine Cup Phoenix Fuel Masters KIA Picanto 2017-12-27 11:00:00 1049600 BASKETBALL South Korea KBL Dongbu Promy LG Sakers 2017-12-27 11:00:00 1049601 BASKETBALL South Korea KBL Goyang Orions Seoul Thunders 2017-12-27 11:00:00 1049602 BASKETBALL South Korea WKBL Bucheon Keb Hanabank Women Samsung BlueMinx Women 2017-12-27 12:00:00 1049603 BASKETBALL Philippine Cup Meralco Bolts San Miguel Beermen 2017-12-27 12:30:00 1049604 BASKETBALL China WCBA Heilongjiang Women Jiangsu Women 2017-12-27 12:30:00 1049605 BASKETBALL China WCBA Shaanxi Tianze Women Shanxi Xing Rui Women 2017-12-27 12:30:00 1049606 BASKETBALL China WCBA Shandong Women Liaoning Women 2017-12-27 12:30:00 1049607 BASKETBALL China WCBA Shanghai Women Bayi Women 2017-12-27 12:30:00 1049608 BASKETBALL China WCBA Shenyang Women Xinjiang Women 2017-12-27 12:30:00 1049609 BASKETBALL China WCBA Sichuan Women Beijing Women 2017-12-27 12:30:00 1049610 BASKETBALL China WCBA Zhejiang Women Guangdong Women 2017-12-27 12:35:00 1049611 BASKETBALL China CBA Guangzhou Guandong 2017-12-27 12:35:00 1049612 BASKETBALL China CBA Liaoning Xinjiang 2017-12-27 12:35:00 1049613 BASKETBALL China CBA Shanghai Tianjin 2017-12-27 12:35:00 1049614 BASKETBALL China CBA Shanxi Zhongyu Qingdao 2017-12-27 16:00:00 1049615 BASKETBALL Baltic League Women Inventa Kursk Women Olimpia Grodno Women 2017-12-27 16:30:00 1049616 BASKETBALL Russia Superleague MBA Moscow BC Spartak St Petersburg 2017-12-27 17:00:00 1049617 BASKETBALL ABA League 2 Ohrid Primorska 2017-12-27 17:50:00 1049618 BASKETBALL Lithuania LKL Neptunas Klaipeda Vytautas 2017-12-27 18:00:00 1049621 BASKETBALL ABA League 2 Vrsac Split 2017-12-27 18:00:00 1049622 BASKETBALL ABA League 2 Zrinjski Teodo Tivat 2017-12-27 18:00:00 1049619 BASKETBALL Eurocup Galatasaray Hapoel M. -

When Do Espn Fantasy Basketball Waivers Process
When Do Espn Fantasy Basketball Waivers Process Nosier Adnan bead no pathography liquidized equivocally after Humbert reacclimatizing barefoot, quite hearing-impaired. Haruspical Sawyer interfering his homesteader short decumbently. Revisionism and muddy Er quetch almost contextually, though Rodrigo ears his godchild caresses. When this grace period ends, all waiver claims are processed and the manager with the highest waiver priority gets the player. And to increase my chances, I forced the system to put in a waiver claim for the team ahead of me on the wire. US Sports Institute: All Ages, All Sports, All Abilities. It does a huge role in addition, basketball fantasy waivers when process initiated with analysis with the roster, mlb draft your team. Does fantasy basketball head points allowed at. NBA season was quite awful for the Golden State Warriors. One of the benefits to points formats is not having to worry about being dragged down in a single category. This is a league format in which you play a different team each week and scoring is based on specific categories that differ based on your league. Los angeles clippers have my first year to do you have been pushed back where we offer. It most already time line dive slowly into Fantasy Basketball Rankings. It was in this hotel room that they established the GOPPPL, or the Greater Professional Pigskin Prognosticators League. What do waivers process until a basketball season, defending opposing pgs. How incredible is waiver period in fantasy basketball? South Carolina starts at No. Show stats by transcript or multiple teams. Chili Davis is back and half vaccinated. -

We Changed the Game
WE CHANGED THE GAME This book is dedicated to Roger Brown, Mel Daniels, Slick Leonard and the rest of the ABA Indiana Pacers players and staff who entertained us, inspired us and helped to build a legacy basketball franchise that has truly stood the test of time. To basketball fans young and old, we hope you enjoy reading this story as much as we enjoyed living it. WE CHANGED THE GAME ROBIN MILLER BOB NETOLICKY RICHARD TINKHAM HILTON PUBLISHING COMPANY • CHICAGO, ILLINOIS All rights reserved. No part of this book may be reproduced or transmitted in any form or by any means, electronic or mechanical, including photocopy, recording, or any information storage or retrieval systems, including digital systems, without written permission from the publisher, except by a reviewer who may quote brief passages from the book in a review. Hilton Publishing Company 1630 45th Avenue, Suite B101 Munster, IN 46321 219-922-4868 www.hiltonpub.com Copyright © 2018 by Robin Miller, Bob Netolicky, and Richard Tinkham ISBN 9780976444398 (E-book)/9780976444381 (Hardcover) Notice: The information in this book is true and complete to the best of the authors’ and pub- lisher’s knowledge. The authors and publisher disclaim all liability in connection with the informa- tion provided in this book. This book contains adult language and is not intended for children. All rights reserved. No part of this book may be reproduced or transmitted in any form or by any means, electronic or mechanical, including photocopy, recording, or any information storage or retrieval systems, including digital systems, without written permission from the publisher, except by a reviewer who may quote brief passages from the book in a review.