DOCSLIB.ORG

1 Section 8.3 Hyperbolas Definition: a Hyperbola Is the Set of All Points, The

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
1 Section 8.3 Hyperbolas Definition: a Hyperbola Is the Set of All Points, The Section 8.3 Hyperbolas Definition: A hyperbola is the set of all points, the difference of whose distances from two fixed points is constant. Each fixed point is called a focus (plural = foci ). The focal axis is the line passing through the foci. 1 Basic “vertical” hyperbola: y2 x 2 a (0,c ) Equation: − = 1 y= − x a2 b 2 b a y= x b a a Asymptotes: y= ± x b Foci: (0,±c ) , where c2= a 2 + b 2 Vertices: (0,±a ) (0,−c ) -a c Eccentricity: ( > )1 a Basic “horizontal” hyperbola: b b y= − x y= x a a x2 y 2 Equation: − = 1 a2 b 2 b Asymptotes: y= ± x a ± 2= 2 + 2 -a a Foci: (c ,0) , where c a b (c ,0) (c ,0) Vertices: (±a ,0) c Eccentricity: ( > )1 a Note: The transverse axis is the line segment joining the two vertices. The conjugate axis is the line segment perpendicular to the transverse axis, passing through the center and extending a distance b on either side of the center. (These terms will make more sense after we do the graphing examples.) 2 3 Graphing hyperbolas: To graph a hyperbola with center at the origin: x2 y 2 y2 x 2 • Rearrange into the form − = 1 or − = 1. a2 b 2 a2 b 2 • Decide if it’s a “horizontal” or “vertical” hyperbola. o if x2 comes first, it’s horizontal (vertices are on x-axis). o If y2 comes first, it’s vertical (vertices are on y-axis). • Use the square root of the number under x2 to determine how far to measure in x- direction. • Use the square root of the number under y2 to determine how far to measure in y- direction. • Draw a box with these measurements. • Draw diagonals through the box. These are the asymptotes. Use the dimensions of the box to determine the slope and write the equations of the asymptotes. • Put the vertices at the edge of the box on the correct axis. Then draw a hyperbola, making sure it approaches the asymptotes smoothly. 2 2 2 2 2 • c= a + b where a and b are the denominators. • The foci are located c units from the center, on the same axis as the vertices. When graphing hyperbolas, you will need to find the orientation, center, values for a, b and c, lengths of transverse and converse axes, vertices, foci, equations of the asymptotes, and eccentricity. 4 x2 y2 Example 1: Find all relevant information and graph − = 1. 36 4 Vertices: Foci: Eccentricity: Transverse Axis: Length of transverse axis: Conjugate axis: Length of conjugate axis: Slant Asymptotes: 5 y2 x 2 Example 2: Find all relevant information and graph − = 1 . 4 9 Vertices: Foci: Eccentricity: Transverse Axis: Length of transverse axis: Conjugate axis: Length of conjugate axis: Slant Asymptotes: 6 The equation of a hyperbola with center not at the origin: Center: (h, k) (xh− )(2 yk − ) 2 (yk− )(2 xh − ) 2 − = 1 or − = 1 a2 b 2 a2 b 2 To graph a hyperbola with center not at the origin: • Rearrange (complete the square if necessary) to look like (xh− )(2 yk − ) 2 (yk− )(2 xh − ) 2 − = 1 or − = 1. a2 b 2 a2 b 2 • Start at the center (h , k ) and then graph it as before. • To write down the equations of the asymptotes, start with the equations of the asymptotes for the similar hyperbola with center at the origin. Then replace x with x− h and replace y with y− k . 7 8 Example 3: Write the equation in standard form, find all relevant information and graph 9x 2 −16 y 2 −18 x + 96 y = 279 . 9 Example 4: Write an equation of the hyperbola with center at (-2, 3), one vertex is at (-2, -2) and eccentricity is 2. Example 5: Write an equation of the hyperbola if the vertices are (4, 0) and (4, 8) and the asymptotes have slopes ±1. 10 Math 1330 - Chapter 8 Systems: Identify Equations, Point of Intersection of Equations Classification of Second Degree Equations When you write a conic section in its general form, you have an equation of the form Ax2+ Bxy + Cy 2 + Dx ++= Ey F 0. (All of the equations we have seen so far have a value for B that is 0.) We graphed the following examples in the past sections: 5x 2 + 5y 2 − 20 x +10 y = 20 (a circle) y 2 − 6y = 8x + 7 (a parabola) 4x2 − 8x + 9y2 − 54 y −= 49 (an ellipse) 9x 2 −16 y 2 −18 x + 96 y = 279 (a hyperbola) With only minimal work, you can determine if an equation in this form is a circle, an ellipse, a parabola or a hyperbola. Identify each conic section from its equation: (x − 2)2 (y + 2)2 a) 12 x = y 2 b) − = 1 9 16 (x + 4)2 (y −1)2 (x + 4)2 (y −1)2 c) + = 1 d) + = 1 4 9 4 4 1 Classification of Second Degree Equations When you write a conic section in its general form, you have an equation of the form Ax 2 + Bxy + Cy 2 + Dx + Ey + F = 0 : If A, B and C are not all 0, and if the graph is not degenerate, then: • The graph is a circle if B 2 − 4AC < 0 and A = C . • The graph is an ellipse if B 2 − 4AC < 0 and A ≠ C . • The graph is a parabola if B 2 − 4AC = 0 . • The graph is a hyperbola if B 2 − 4AC > 0 . Remember, if there is no “xy” term, then B = 0. Example: Identify each conic. (Note, none of these are degenerates conics.) a. 6x 2 − 4xy + 3y 2 + 5x − 7y + 3 = 0 b. 2x 2 − 8y 2 − 6x −16 y − 25 = 0 c. − 3x 2 + 5x −12 y − 7 = 0 d. 4x 2 + 4y 2 − 24 x −16 y − 72 = 0 2 Sometimes equations that look like they should be conic sections do not behave very well. Example 1 : Graph (x − 3)2 + (y +1)2 = 0 Example 2: Graph 9x 2 − 4y 2 = 0 3 Example 3: Graph 2y + (x + 2)2 = 2y Example 4: Graph 2x 2 + 3y 2 = −1 These are all examples of degenerate conic sections . Instead of getting the graphs you expect, you have a point (Example 1), two lines (Example 2) and a single line (Example 3) and no graph at all (Example 4). You will not see these very often, but you should be aware of them. 4 Systems of Second Degree Equations When we graph two conic sections or a conic section and a line on the same coordinate plane, their graphs may contain points of intersection. The graph below shows a hyperbola and a line and contains two points of intersection. We want to be able to find the points of intersection. To do this, we will solve a system of equations, but now one or both of the equations will be second degree equations. Determining the points of intersection graphically is difficult, so we will do these algebraically. Example 5: Determine the number of points of intersection for the system. x2 y 2 − = 1 9 9 y2 = 4 x 5 Example 6: Solve the system of equations: x 2 + y 2 = 4 4x 2 − y 2 = 1 6 Example 7: Solve the system of equations: f ()x = x 2 − 4x +11 g()x = 5x − 3 7 Example 8: Solve the system of equations: x 2 + y 2 = 9 ()x + y 2 = 9 8 Example 9: Graph each and determine the number of points of intersection. x2+ y 2 = 16 x2 y 2 + = 1 9 4 9.
Load more

Recommended publications
  • Combination of Cubic and Quartic Plane Curve
    IOSR Journal of Mathematics (IOSR-JM) e-ISSN: 2278-5728,p-ISSN: 2319-765X, Volume 6, Issue 2 (Mar. - Apr. 2013), PP 43-53 www.iosrjournals.org Combination of Cubic and Quartic Plane Curve C.Dayanithi Research Scholar, Cmj University, Megalaya Abstract The set of complex eigenvalues of unistochastic matrices of order three forms a deltoid. A cross-section of the set of unistochastic matrices of order three forms a deltoid. The set of possible traces of unitary matrices belonging to the group SU(3) forms a deltoid. The intersection of two deltoids parametrizes a family of Complex Hadamard matrices of order six. The set of all Simson lines of given triangle, form an envelope in the shape of a deltoid. This is known as the Steiner deltoid or Steiner's hypocycloid after Jakob Steiner who described the shape and symmetry of the curve in 1856. The envelope of the area bisectors of a triangle is a deltoid (in the broader sense defined above) with vertices at the midpoints of the medians. The sides of the deltoid are arcs of hyperbolas that are asymptotic to the triangle's sides. I. Introduction Various combinations of coefficients in the above equation give rise to various important families of curves as listed below. 1. Bicorn curve 2. Klein quartic 3. Bullet-nose curve 4. Lemniscate of Bernoulli 5. Cartesian oval 6. Lemniscate of Gerono 7. Cassini oval 8. Lüroth quartic 9. Deltoid curve 10. Spiric section 11. Hippopede 12. Toric section 13. Kampyle of Eudoxus 14. Trott curve II. Bicorn curve In geometry, the bicorn, also known as a cocked hat curve due to its resemblance to a bicorne, is a rational quartic curve defined by the equation It has two cusps and is symmetric about the y-axis.
    [Show full text]
  • Device Constructions with Hyperbolas
    Device Constructions with Hyperbolas Alfonso Croeze1 William Kelly1 William Smith2 1Department of Mathematics Louisiana State University Baton Rouge, LA 2Department of Mathematics University of Mississippi Oxford, MS July 8, 2011 Croeze, Kelly, Smith LSU&UoM Device Constructions with Hyperbolas Hyperbola Definition Conic Section Croeze, Kelly, Smith LSU&UoM Device Constructions with Hyperbolas Hyperbola Definition Conic Section Two Foci Focus and Directrix Croeze, Kelly, Smith LSU&UoM Device Constructions with Hyperbolas The Project Basic constructions Constructing a Hyperbola Advanced constructions Croeze, Kelly, Smith LSU&UoM Device Constructions with Hyperbolas Rusty Compass Theorem Given a circle centered at a point A with radius r and any point C different from A, it is possible to construct a circle centered at C that is congruent to the circle centered at A with a compass and straightedge. Croeze, Kelly, Smith LSU&UoM Device Constructions with Hyperbolas X B C A Y Croeze, Kelly, Smith LSU&UoM Device Constructions with Hyperbolas X D B C A Y Croeze, Kelly, Smith LSU&UoM Device Constructions with Hyperbolas A B X Y Angle Duplication A X Croeze, Kelly, Smith LSU&UoM Device Constructions with Hyperbolas Angle Duplication A X A B X Y Croeze, Kelly, Smith LSU&UoM Device Constructions with Hyperbolas C Z A B X Y C Z A B X Y Croeze, Kelly, Smith LSU&UoM Device Constructions with Hyperbolas C Z A B X Y C Z A B X Y Croeze, Kelly, Smith LSU&UoM Device Constructions with Hyperbolas Constructing a Perpendicular C C A B Croeze, Kelly, Smith LSU&UoM Device Constructions with Hyperbolas C C X X O A B A B Y Y Croeze, Kelly, Smith LSU&UoM Device Constructions with Hyperbolas We needed a way to draw a hyperbola.
    [Show full text]
  • Polynomial Curves and Surfaces
    Polynomial Curves and Surfaces Chandrajit Bajaj and Andrew Gillette September 8, 2010 Contents 1 What is an Algebraic Curve or Surface? 2 1.1 Algebraic Curves . .3 1.2 Algebraic Surfaces . .3 2 Singularities and Extreme Points 4 2.1 Singularities and Genus . .4 2.2 Parameterizing with a Pencil of Lines . .6 2.3 Parameterizing with a Pencil of Curves . .7 2.4 Algebraic Space Curves . .8 2.5 Faithful Parameterizations . .9 3 Triangulation and Display 10 4 Polynomial and Power Basis 10 5 Power Series and Puiseux Expansions 11 5.1 Weierstrass Factorization . 11 5.2 Hensel Lifting . 11 6 Derivatives, Tangents, Curvatures 12 6.1 Curvature Computations . 12 6.1.1 Curvature Formulas . 12 6.1.2 Derivation . 13 7 Converting Between Implicit and Parametric Forms 20 7.1 Parameterization of Curves . 21 7.1.1 Parameterizing with lines . 24 7.1.2 Parameterizing with Higher Degree Curves . 26 7.1.3 Parameterization of conic, cubic plane curves . 30 7.2 Parameterization of Algebraic Space Curves . 30 7.3 Automatic Parametrization of Degree 2 Curves and Surfaces . 33 7.3.1 Conics . 34 7.3.2 Rational Fields . 36 7.4 Automatic Parametrization of Degree 3 Curves and Surfaces . 37 7.4.1 Cubics . 38 7.4.2 Cubicoids . 40 7.5 Parameterizations of Real Cubic Surfaces . 42 7.5.1 Real and Rational Points on Cubic Surfaces . 44 7.5.2 Algebraic Reduction . 45 1 7.5.3 Parameterizations without Real Skew Lines . 49 7.5.4 Classification and Straight Lines from Parametric Equations . 52 7.5.5 Parameterization of general algebraic plane curves by A-splines .
    [Show full text]
  • Construction of Rational Surfaces of Degree 12 in Projective Fourspace
    Construction of Rational Surfaces of Degree 12 in Projective Fourspace Hirotachi Abo Abstract The aim of this paper is to present two different constructions of smooth rational surfaces in projective fourspace with degree 12 and sectional genus 13. In particular, we establish the existences of five different families of smooth rational surfaces in projective fourspace with the prescribed invariants. 1 Introduction Hartshone conjectured that only finitely many components of the Hilbert scheme of surfaces in P4 contain smooth rational surfaces. In 1989, this conjecture was positively solved by Ellingsrud and Peskine [7]. The exact bound for the degree is, however, still open, and hence the question concerning the exact bound motivates us to find smooth rational surfaces in P4. The goal of this paper is to construct five different families of smooth rational surfaces in P4 with degree 12 and sectional genus 13. The rational surfaces in P4 were previously known up to degree 11. In this paper, we present two different constructions of smooth rational surfaces in P4 with the given invariants. Both the constructions are based on the technique of “Beilinson monad”. Let V be a finite-dimensional vector space over a field K and let W be its dual space. The basic idea behind a Beilinson monad is to represent a given coherent sheaf on P(W ) as a homology of a finite complex whose objects are direct sums of bundles of differentials. The differentials in the monad are given by homogeneous matrices over an exterior algebra E = V V . To construct a Beilinson monad for a given coherent sheaf, we typically take the following steps: Determine the type of the Beilinson monad, that is, determine each object, and then find differentials in the monad.
    [Show full text]
  • Apollonius of Pergaconics. Books One - Seven
    APOLLONIUS OF PERGACONICS. BOOKS ONE - SEVEN INTRODUCTION A. Apollonius at Perga Apollonius was born at Perga (Περγα) on the Southern coast of Asia Mi- nor, near the modern Turkish city of Bursa. Little is known about his life before he arrived in Alexandria, where he studied. Certain information about Apollonius’ life in Asia Minor can be obtained from his preface to Book 2 of Conics. The name “Apollonius”(Apollonius) means “devoted to Apollo”, similarly to “Artemius” or “Demetrius” meaning “devoted to Artemis or Demeter”. In the mentioned preface Apollonius writes to Eudemus of Pergamum that he sends him one of the books of Conics via his son also named Apollonius. The coincidence shows that this name was traditional in the family, and in all prob- ability Apollonius’ ancestors were priests of Apollo. Asia Minor during many centuries was for Indo-European tribes a bridge to Europe from their pre-fatherland south of the Caspian Sea. The Indo-European nation living in Asia Minor in 2nd and the beginning of the 1st millennia B.C. was usually called Hittites. Hittites are mentioned in the Bible and in Egyptian papyri. A military leader serving under the Biblical king David was the Hittite Uriah. His wife Bath- sheba, after his death, became the wife of king David and the mother of king Solomon. Hittites had a cuneiform writing analogous to the Babylonian one and hi- eroglyphs analogous to Egyptian ones. The Czech historian Bedrich Hrozny (1879-1952) who has deciphered Hittite cuneiform writing had established that the Hittite language belonged to the Western group of Indo-European languages [Hro].
    [Show full text]
  • A Brief Note on the Approach to the Conic Sections of a Right Circular Cone from Dynamic Geometry
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by EPrints Complutense A brief note on the approach to the conic sections of a right circular cone from dynamic geometry Eugenio Roanes–Lozano Abstract. Nowadays there are different powerful 3D dynamic geometry systems (DGS) such as GeoGebra 5, Calques 3D and Cabri Geometry 3D. An obvious application of this software that has been addressed by several authors is obtaining the conic sections of a right circular cone: the dynamic capabilities of 3D DGS allows to slowly vary the angle of the plane w.r.t. the axis of the cone, thus obtaining the different types of conics. In all the approaches we have found, a cone is firstly constructed and it is cut through variable planes. We propose to perform the construction the other way round: the plane is fixed (in fact it is a very convenient plane: z = 0) and the cone is the moving object. This way the conic is expressed as a function of x and y (instead of as a function of x, y and z). Moreover, if the 3D DGS has algebraic capabilities, it is possible to obtain the implicit equation of the conic. Mathematics Subject Classification (2010). Primary 68U99; Secondary 97G40; Tertiary 68U05. Keywords. Conics, Dynamic Geometry, 3D Geometry, Computer Algebra. 1. Introduction Nowadays there are different powerful 3D dynamic geometry systems (DGS) such as GeoGebra 5 [2], Calques 3D [7, 10] and Cabri Geometry 3D [11]. Focusing on the most widespread one (GeoGebra 5) and conics, there is a “conics” icon in the ToolBar.
    [Show full text]
  • Chapter 9: Conics Section 9.1 Ellipses
    Chapter 9: Conics Section 9.1 Ellipses ..................................................................................................... 579 Section 9.2 Hyperbolas ............................................................................................... 597 Section 9.3 Parabolas and Non-Linear Systems ......................................................... 617 Section 9.4 Conics in Polar Coordinates..................................................................... 630 In this chapter, we will explore a set of shapes defined by a common characteristic: they can all be formed by slicing a cone with a plane. These families of curves have a broad range of applications in physics and astronomy, from describing the shape of your car headlight reflectors to describing the orbits of planets and comets. Section 9.1 Ellipses The National Statuary Hall1 in Washington, D.C. is an oval-shaped room called a whispering chamber because the shape makes it possible for sound to reflect from the walls in a special way. Two people standing in specific places are able to hear each other whispering even though they are far apart. To determine where they should stand, we will need to better understand ellipses. An ellipse is a type of conic section, a shape resulting from intersecting a plane with a cone and looking at the curve where they intersect. They were discovered by the Greek mathematician Menaechmus over two millennia ago. The figure below2 shows two types of conic sections. When a plane is perpendicular to the axis of the cone, the shape of the intersection is a circle. A slightly titled plane creates an oval-shaped conic section called an ellipse. 1 Photo by Gary Palmer, Flickr, CC-BY, https://www.flickr.com/photos/gregpalmer/2157517950 2 Pbroks13 (https://commons.wikimedia.org/wiki/File:Conic_sections_with_plane.svg), “Conic sections with plane”, cropped to show only ellipse and circle by L Michaels, CC BY 3.0 This chapter is part of Precalculus: An Investigation of Functions © Lippman & Rasmussen 2020.
    [Show full text]
  • 14. Mathematics for Orbits: Ellipses, Parabolas, Hyperbolas Michael Fowler
    14. Mathematics for Orbits: Ellipses, Parabolas, Hyperbolas Michael Fowler Preliminaries: Conic Sections Ellipses, parabolas and hyperbolas can all be generated by cutting a cone with a plane (see diagrams, from Wikimedia Commons). Taking the cone to be xyz222+=, and substituting the z in that equation from the planar equation rp⋅= p, where p is the vector perpendicular to the plane from the origin to the plane, gives a quadratic equation in xy,. This translates into a quadratic equation in the plane—take the line of intersection of the cutting plane with the xy, plane as the y axis in both, then one is related to the other by a scaling xx′ = λ . To identify the conic, diagonalized the form, and look at the coefficients of xy22,. If they are the same sign, it is an ellipse, opposite, a hyperbola. The parabola is the exceptional case where one is zero, the other equates to a linear term. It is instructive to see how an important property of the ellipse follows immediately from this construction. The slanting plane in the figure cuts the cone in an ellipse. Two spheres inside the cone, having circles of contact with the cone CC, ′, are adjusted in size so that they both just touch the plane, at points FF, ′ respectively. It is easy to see that such spheres exist, for example start with a tiny sphere inside the cone near the point, and gradually inflate it, keeping it spherical and touching the cone, until it touches the plane. Now consider a point P on the ellipse.
    [Show full text]
  • 2.3 Conic Sections: Hyperbola ( ) ( ) ( )
    2.3 Conic Sections: Hyperbola Hyperbola (locus definition) Set of all points (x, y) in the place such that the absolute value of the difference of each distances from F1 and F2 to (x, y) is a constant distance, d. In the figure above: The distance from F1 to (x1, y1 ) - the distance from F2 to (x1, y1 ) = d and The distance from F1 to (x2 , y2 ) - the distance from F2 to (x2 , y2 ) = d Standard Form of a Hyperbola: Horizontal Hyperbola Vertical Hyperbola 2 2 2 2 (x − h) (y − k) (y − k) (x − h) 2 − 2 = 1 2 − 2 = 1 a b a b center = (h,k) 2a = distance between vertices c = distance from center to focus c2 = a2 + b2 c eccentricity e = ( e > 1 for a hyperbola) a Conjugate axis = 2b Transverse axis = 2a Horizontal Asymptotes Vertical Asymptotes b a y − k = ± (x − h) y − k = ± (x − h) a b Show how d = 2a 2 (x − 2) y2 Ex. Graph − = 1 4 25 Center: (2, 0) Vertices (4, 0) & (0, 0) Foci (2 ± 29,0) 5 Asymptotes: y = ± (x − 2) 2 Ex. Graph 9y2 − x2 − 6x −10 = 0 9y2 − x2 − 6x = 10 9y2 −1(x2 + 6x + 9) = 10 − 9 2 9y2 −1(x + 3) = 1 2 9y2 1(x + 3) 1 − = 1 1 1 2 y2 x + 3 ( ) 1 1 − = 9 1 Center: (-3, 0) ⎛ 1⎞ ⎛ 1⎞ Vertices −3, & −3,− ⎝⎜ 3⎠⎟ ⎝⎜ 3⎠⎟ ⎛ 10 ⎞ Foci −3,± ⎝⎜ 3 ⎠⎟ 1 Asymptotes: y = ± (x + 3) 3 Hyperbolas can be used in so-called ‘trilateration’ or ‘positioning’ problems. The procedure outlined in the next example is the basis of the Long Range Aid to Navigation (LORAN) system, (outdated now due to GPS) Ex.
    [Show full text]
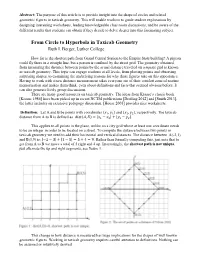
  • From Circle to Hyperbola in Taxicab Geometry
    Abstract: The purpose of this article is to provide insight into the shape of circles and related geometric figures in taxicab geometry. This will enable teachers to guide student explorations by designing interesting worksheets, leading knowledgeable class room discussions, and be aware of the different results that students can obtain if they decide to delve deeper into this fascinating subject. From Circle to Hyperbola in Taxicab Geometry Ruth I. Berger, Luther College How far is the shortest path from Grand Central Station to the Empire State building? A pigeon could fly there in a straight line, but a person is confined by the street grid. The geometry obtained from measuring the distance between points by the actual distance traveled on a square grid is known as taxicab geometry. This topic can engage students at all levels, from plotting points and observing surprising shapes, to examining the underlying reasons for why these figures take on this appearance. Having to work with a new distance measurement takes everyone out of their comfort zone of routine memorization and makes them think, even about definitions and facts that seemed obvious before. It can also generate lively group discussions. There are many good resources on taxicab geometry. The ideas from Krause’s classic book [Krause 1986] have been picked up in recent NCTM publications [Dreiling 2012] and [Smith 2013], the latter includes an extensive pedagogy discussion. [House 2005] provides nice worksheets. Definition: Let A and B be points with coordinates (푥1, 푦1) and (푥2, 푦2), respectively. The taxicab distance from A to B is defined as 푑푖푠푡(퐴, 퐵) = |푥1 − 푥2| + |푦1 − 푦2|.
    [Show full text]
  • Ellipse, Hyperbola and Their Conjunction Arxiv:1805.02111V2
    Ellipse, Hyperbola and Their Conjunction Arkadiusz Kobiera Warsaw University of Technology Abstract This article presents a simple analysis of cones which are used to generate a given conic curve by section by a plane. It was found that if the given curve is an ellipse, then the locus of vertices of the cones is a hyperbola. The hyperbola has foci which coincidence with the ellipse vertices. Similarly, if the given curve is the hyperbola, the locus of vertex of the cones is the ellipse. In the second case, the foci of the ellipse are located in the hyperbola's vertices. These two relationships create a kind of conjunction between the ellipse and the hyperbola which originate from the cones used for generation of these curves. The presented conjunction of the ellipse and hyperbola is a perfect example of mathematical beauty which may be shown by the use of very simple geometry. As in the past the conic curves appear to be arXiv:1805.02111v2 [math.HO] 26 Jan 2019 very interesting and fruitful mathematical beings. 1 Introduction The conical curves are mathematical entities which have been known for thousands years since the first Menaechmus' research around 250 B.C. [2]. Anybody who has attempted undergraduate course of geometry knows that ellipse, hyperbola and parabola are obtained by section of a cone by a plane. Every book dealing with the this subject has a sketch where the cone is sec- tioned by planes at various angles, which produces different kinds of conics. Usually authors start with the cone to produce the conic curve by section.
    [Show full text]
  • A Conic Sections
    A Conic Sections The ellipse, hyperbola, and parabola (and also the circle, which is a special case of the ellipse) are called the conic section curves (or the conic sections or just conics), since they can be obtained by cutting a cone with a plane (i.e., they are the intersections of a cone and a plane). The conics are easy to calculate and to display, so they are commonly used in applications where they can approximate the shape of other, more complex, geometric figures. Many natural motions occur along an ellipse, parabola, or hyperbola, making these curves especially useful. Planets move in ellipses; many comets move along a hyperbola (as do many colliding charged particles); objects thrown in a gravitational field follow a parabolic path. There are several ways to define and represent these curves and this section uses asimplegeometric definition that leads naturally to the parametric and the implicit representations of the conics. y F P D P D F x (a) (b) Figure A.1: Definition of Conic Sections. Definition: A conic is the locus of all the points P that satisfy the following: The distance of P from a fixed point F (the focus of the conic, Figure A.1a) is proportional 364 A. Conic Sections to its distance from a fixed line D (the directrix). Using set notation, we can write Conic = {P|PF = ePD}, where e is the eccentricity of the conic. It is easy to classify conics by means of their eccentricity: =1, parabola, e = < 1, ellipse (the circle is the special case e = 0), > 1, hyperbola.
    [Show full text]