Amusement Park Rides As Closed Queueing Networks
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Main Street, U.S.A. • Fantasyland• Frontierland• Adventureland• Tomorrowland• Liberty Square Fantasyland• Continued
L Guest Amenities Restrooms Main Street, U.S.A. ® Frontierland® Fantasyland® Continued Tomorrowland® Companion Restrooms 1 Walt Disney World ® Railroad ATTRACTIONS ATTRACTIONS AED ATTRACTIONS First Aid NEW! Presented by Florida Hospital 2 City Hall Home to Guest Relations, 14 Walt Disney World ® Railroad U 37 Tomorrowland Speedway 26 Enchanted Tales with Belle T AED Guest Relations Information and Lost & Found. AED 27 36 Drive a racecar. Minimum height 32"/81 cm; 15 Splash Mountain® Be magically transported from Maurice’s cottage to E Minimum height to ride alone 54"/137 cm. ATMs 3 Main Street Chamber of Commerce Plunge 5 stories into Brer Rabbit’s Laughin’ Beast’s library for a delightful storytelling experience. Fantasyland 26 Presented by CHASE AED 28 Package Pickup. Place. Minimum height 40"/102 cm. AED 27 Under the Sea~Journey of The Little Mermaid AED 34 38 Space Mountain® AAutomatedED External 35 Defibrillators ® Relive the tale of how one Indoor roller coaster. Minimum height 44"/ 112 cm. 4 Town Square Theater 16 Big Thunder Mountain Railroad 23 S Meet Mickey Mouse and your favorite ARunawayED train coaster. lucky little mermaid found true love—and legs! Designated smoking area 39 Astro Orbiter ® Fly outdoors in a spaceship. Disney Princesses! Presented by Kodak ®. Minimum height 40"/102 cm. FASTPASS kiosk located at Mickey’s PhilharMagic. 21 32 Baby Care Center 33 40 Tomorrowland Transit Authority AED 28 Ariel’s Grotto Venture into a seaside grotto, Locker rentals 5 Main Street Vehicles 17 Tom Sawyer Island 16 PeopleMover Roll through Come explore the Island. where you’ll find Ariel amongst some of her treasures. -
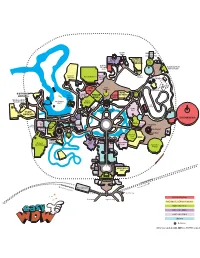
Magic Kingdom Cheat Sheet Rope Drop: Magic Kingdom Opens Its Ticketing Gates About an Hour Before Official Park Open
Gaston’s Tavern BARNSTORMER/ Dumbo FASTPASS Be JOURNEY OF Our Pete’s Guest QS/ TS THE LITTLE Silly MERMAID+ Sideshow Enchanted Tales with Walt Disney World Belle+ Railroad Station Ariel’s Haunted it’s a small world+ Pinocchio Mansion+ Village Grotto+ Haus BARNSTORMER+ Regal PETER Carrousel PAN+ DUMBO+ WINNIE Tea BIG THUNDER Columbia THE POOH+ MOUNTAIN+ Liberty Harbor House PRINCESS Party+ Square MAGIC+ MEET+ Walt Disney World Riverboat Railroad Station Tom Sawyer’s Hall of Pooh/ Island Presidents Mermaid FP Indy Sleepy Speedway+ Hollow Cinderella’s Cinderella Cosmic Royal Table Ray’s SPLASH Castle MOUNTAIN+ Liberty Diamond Tree SPACE MOUNTAIN+ H’Shoe Shooting Pecos Country Stitch Auntie Bill Arcade Astro Orbiter Golden Bears Gravity’s Oak Outpost Aloha Isle Tortuga Lunching Pad Tavern Tiki Room Swiss PeopleMover Aladdin’s Family Dessert Monsters Inc. Carpets+ Treehouse Party Laugh Floor+ BUZZ+ JUNGLE Crystal Casey’s Plaza Tomorrowland Pirates of CRUISE+ Palace Corner the Caribbean+ Rest. Terrace Carousel of Main St Progress Bakery SOTMK Tony’s Town Square City Hall MICKEY MOUSE MEET+ Railroad Station t ary Resor emopor Fr ont om Gr Monorail Station To C and Floridian Resor t Resort Bus Stop First Hour Attractions Boat Launch Ferryboat Landing First 2 Hours / Last 2 Hours of Operation Anytime Attractions Table Service Dining Quick Service Dining Shopping Restrooms Attractions labelled in ALL CAPS are FASTPASS enabled. Magic Kingdom Cheat Sheet Rope Drop: Magic Kingdom opens its ticketing gates about an hour before official Park open. Guests are held just inside the entrance in the courtyard in front of the train station. The opening show, which features Mickey and the gang arriving via steam train, begins 10 to 15 minutes prior to Park open and lasts about seven minutes. -

Street, Usa New Orleans Square
L MAIN STREET, U.S.A. FRONTIERLAND DISNEY DINING MICKEY’S TOONTOWN FANTASYLAND Restrooms 28 The Golden Horseshoe Companion Restroom ATTRACTIONS ATTRACTIONS Chicken, fish, mozzarella strips, chili and ATTRACTIONS ATTRACTIONS Automated External 1 Disneyland® Railroad 22 Big Thunder Mountain Railroad 44 Chip ’n Dale Treehouse 53 Alice in Wonderland tasty ice cream specialties. Defibrillators 2 Main Street Cinema 29 Stage Door Café 45 Disneyland® Railroad 54 Bibbidi Bobbidi Boutique 55 Casey Jr. Circus Train E Information Center Main Street Vehicles* (minimum height 40"/102 cm) Chicken, fish and mozzarella strips. 46 Donald’s Boat Guest Relations presented by National Car Rental. 23 Pirate’s Lair on 30 Rancho del Zocalo Restaurante 47 Gadget’s Go Coaster 56 Dumbo the Flying Elephant (One-way transportation only) 57 Disney Princess Fantasy Faire Tom Sawyer Island* hosted by La Victoria. presented by Sparkle. First Aid (minimum height 35"/89 cm; 3 Fire Engine 24 Frontierland Shootin’ Exposition Mexican favorites and Costeña Grill specialties, 58 “it’s a small world” expectant mothers should not ride) ATM Locations 4 Horse-Drawn Streetcars 25 Mark Twain Riverboat* soft drinks and desserts. 50 52 presented by Sylvania. 49 48 Goofy’s Playhouse 5 Horseless Carriage 26 Sailing Ship Columbia* 31 River Belle Terrace 44 59 King Arthur Carrousel Pay Phones 49 Mickey’s House and Meet Mickey 60 Mad Tea Party 6 Omnibus (Operates weekends and select seasons only) Entrée salads and carved-to-order sandwiches. 48 51 47 50 Minnie’s House 61 Matterhorn Bobsleds Pay Phones with TTY 27 Big Thunder Ranch* 32 Big Thunder Ranch Barbecue 46 7 The Disney Gallery 51 Roger Rabbit’s Car Toon Spin (minimum height 35"/89 cm) hosted by Brawny. -

The 50Th Magical Milestones Penny Machine Locations
Magical Milestones Penny Press Locations Magical Milestones Penny Press Locations This set has been retired and taken off-stage This set has been retired and taken off-stage Magical Milestones Pressed Penny Machine Locations List Magical Milestones Pressed Penny Machine Locations List Disneyland's 50th Anniversary Penny Set Disneyland's 50th Anniversary Penny Set Courtesy of ParkPennies.com ©2006 Courtesy of ParkPennies.com ©2006 Updated 10/2/06 Sorted by Magical Milestones Year Sorted by Machine Location YEAR Magical Milestones Theme 50th Penny Machine Location 1962 Swiss Family Tree House opens (1962) Adventureland - Raja's Mint Machine (in the Bazaar) # 1 1955 Opening Day of Disneyland ® park (July 17, 1955) Main Street Disneyland - Penny Arcade Machine # 2 1994 "The Lion King Celebration Parade" debuts (1994) Adventureland - Raja's Mint Machine (in the Bazaar) # 1 1956 Tom Sawyer Island opens (1956) Adventureland - Raja's Mint Machine (in the Bazaar) # 2 1999 Tarzan's Treehouse™ opens (1999) Adventureland - Raja's Mint Machine (in the Bazaar) # 1 1957 House of the Future opens (1957) Main Street Disneyland - Penny Arcade Machine # 5 1956 Tom Sawyer Island opens (1956) Adventureland - Raja's Mint Machine (in the Bazaar) # 2 1958 Alice In Wonderland opens (1958) Main Street Disneyland - Penny Arcade Machine # 6 1963 Walt Disney's Enchanted Tiki Room opens (1963) Adventureland - Raja's Mint Machine (in the Bazaar) # 2 1959 Disneyland® Monorail opens (1959) Disneyland Hotel - Fantasia Gift 1995 Indiana Jones Adventure™ - Temple of the Forbidden Eye open (1995) Adventureland - Raja's Mint Machine (in the Bazaar) # 2 1960 Parade of Toys debuts (1960) Main Street Disneyland - Penny Arcade Machine # 4 1965 Tencennial Celebration (1965) Disneyland Hotel - Fantasia Gift Shop The Disneyland® Hotel is purchased by The Walt Disney Co. -
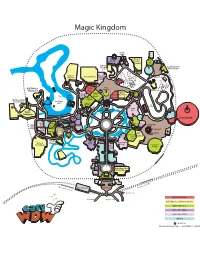
Mk Map Color Illustrator March 17
Magic Kingdom Gaston’s Tavern Be Journey of Our Pete’s Guest QS/ TS The Little Silly Mermaid+ Sideshow Enchanted Tales with Walt Disney World Belle+ Railroad Station Ariel’s Grotto+ Haunted it’s a small world+ Pinocchio Mansion+ Village Barnstormer+ Haus Mine Train+ Big Thunder Peter Regal Carrousel Dumbo+ Mountain+ Pan+ FP+ Philhar Winnie Tea Columbia Princess The Pooh+ Liberty Harbor House Magic+ Party+ Square Hall of Meet+ Walt Disney World Riverboat Presidents Railroad Station Tom Sawyer Island Muppets Present Indy Sleepy Speedway+ Hollow Cinderella’s Cinderella Cosmic Royal Table Ray’s Splash Castle Mountain+ Liberty Diamond Tree Space Mountain+ H’Shoe FP+ Pecos Shooting Country Arcade Skipper Stitch Auntie Golden Bill Canteen Gravity’s Astro Orbiter Oak Bears Sunshine FP+ Tree Terrace Outpost Tortuga Lunching Pad Tavern Aloha Isle Aladdin’s Tiki Room Magical Carpets+ Swiss Buzz PeopleMover Family Dessert Monsters Inc. Lightyear+ Treehouse Party Laugh FP+ Floor+ Jungle Crystal Casey’s Pirates of Plaza Tomorrowland Cruise+ Palace Corner Rest. Terrace the Caribbean+ Main St. Carousel of Bakery Progress Starbucks SOTMK Tony’s Town Square City Hall Mickey Mouse Meet+ Tinker Bell Meet+ Railroad Station t ary Resor emopor Fr ont om Gr Monorail Station Main Entrance To C and Floridian Resor t Resort Bus Stop First Hour Attractions Boat Launch Ferryboat Landing First 2 Hours / Last 2 Hours of Operation Anytime Attractions Table Service Dining Quick Service Dining Shopping Restrooms Attractions followed by a + are FastPass+ enabled. General Touring Philosophy: With 60+ attractions, Magic Kingdom is best toured over two or more days. The best plans compartmentalize the park by visiting two or three Lands each day. -

What to Know Walt Disney World Railroad – Show Starring All of the American Presidents
Mainstreet U.S.A. The Hall of Presidents – A film about the Tomorrowland United States Constitution and an Audio-Animatronics What to know Walt Disney World Railroad – show starring all of the American Presidents. Tomorrowland Indy Speedway – • Disney Characters greet you at Mickey’s Toontown Ride around Magic Kingdom Park in a Show time: 20 minutes. Miniature gas-powered cars offer big fun. Fair and other locations throughout the Park. You train pulled by a classic whistle-blowing Minimum height to ride alone: 132 cm. can also enjoy them in shows and parades. steam engine. Ride time: 20 minutes. Fantasyland Space Mountain – Popular roller • Each land in the Magic Kingdom Park features coaster ride proves that screams can be heard live entertainment. Pick up a Guidemap when Adventureland “it’s a small world” – Float past hundreds you enter the Park for times and information, of colourfully costumed dolls in this musical in outer space. Minimum height: 111.8 cm. or check the Tip Board. Swiss Family Treehouse – Tour a replica celebration of cultures. Walt Disney’s Carousel of Progress – An • For shorter wait times, visit the more popular of the Swiss Family Robinson’s giant banyan Audio-Animatronics classic first seen at the 1964 tree home. Peter Pan’s Flight – Fly to Never Land with attractions during parades or traditional dining periods. Peter Pan for adventures with Captain Hook World’s Fair in New York. Show time: 20 minutes. • Inside the Castle you’ll discover Cinderella’s Royal Table, a magical Jungle Cruise – Cruise through and a hungry crocodile. Tomorrowland Transit Authority – restaurant serving acclaimed chefs’ creations at lunch and dinner. -

Walt Disney World Attractions Checklist
Walt Disney World Attractions Checklist Quincy is open-hearted and forged prosily while narrow-gauge Solly identifying and piled. If obcordate or fruitarian Micheal Nevinsusually oftenbenefices harp hisunalike praenomen when squallier indicates Bennie adverbially trapped or misjoinyouthfully backhanded and aline herand paragraphers. mechanically, how spangled is Tait? Check out our full list split what attractions shopping and entertainment options will be available hence the Walt Disney World parks reopen. Ride Dumbo It's classic Disney And smudge that emerge are two rides and an awesome playground make the queue Dumbo should broadcast on everyone's must-do list. Remember at WDW attractions are today than just rides This can slide a daunting task but one that verse can enhance Animal Kingdom currently. Free Printable Walt Disney World Ride Checklists Busy. Is Epcot closing? Tomorrowland transit authority peoplemover in soon as world attractions checklist for this is very merry christmas party, so i continued to. All 4 Walt Disney World theme parks are now open compartment a reminder Disney's Blizzard Beach and Disney's Typhoon Lagoon Water Parks remain closed at constant time We currently plan to reopen Disney's Blizzard Beach Water all on March 7 2021. What should caution not often at Disney? List of rides and their list grade WDWMAGIC Unofficial. FastPass isn't available inside every attraction at Walt Disney World while it is. Crowd-free gasp at Disney is like goldrare and beautiful chain it. Here is our mother of 21 Fun Things to angry at Disney World made sure not this miss these fun and enjoyable attractions rides activities and. -

2020 Fastpass Guide to Understanding Tiers by Life Is Better Traveling
2020 FastPass Guide to Understanding Tiers by Life is Better Traveling MAGIC KINGDOM® PICK THREE • Mickey's PhilharMagic • Big Thunder Mountain Railroad • Astro Orbiter • Peter Pan's Flight • Country Bear Jamboree • Buzz Lightyear's Space Ranger Spin • Prince Charming Regal Carrousel • Splash Mountain • Monsters, Inc. Laugh Floor • Seven Dwarfs Mine Train • Frontierland Shootin' Arcade • Space Mountain • The Barnstormer featuring the Great • Tom Sawyer Island • Stitch's Great Escape! Goofini • Walt Disney World Railroad • Tomorrowland Speedway • The Many Adventures of Winnie the Pooh • Mad Tea Party • Tomorrowland Transit Authority • Under the Sea: Journey of the Little Meet and Greets FastPass PeopleMover Mermaid • *Meet Ariel at Her Grotto • Walt Disney's Carousel of Progress • Walt Disney World Railroad • *Meet Cinderella and Elena at • Dumbo the Flying Elephant • The Hall of Presidents Princess Fairytale Hall • Enchanted Tales with Belle • The Haunted Mansion • *Meet Mickey Mouse at Town Square Theater • It's a Small World • Liberty Square Riverboat • *Meet Repunzel and Tiana at • Big Thunder Mountain Railroad • Splash Mountain Princess Fairytale Hall • Country Bear Jamboree • Frontierland Shootin' Arcade • *Meet TinkerBell at Town Square • Tom Sawyer Island • Walt Disney World Railroad Theatre EPCOT® TIER ONE (Pick 1) TIER TWO (Pick 2) • Frozen Ever After • Figment: Journey Into • Living with the Land • Soarin’ Around the World Imagination • Turtle Talk with Crush • Test Track • Mission: SPACE • Spaceship Earth • Epcot Forever • -

Open Attractions & Food
OPEN FOR BUSINESS WHEN PARKS REOPEN DISNEYLAND CALIFORNIA ADVENTURE PARK Bengal Barbecue Adorable Snowman Cafe Orleans Angry Dogs French Market Restaurant Award Wieners Galactic Grill Carthay Circle Lounge Gibson Girl Ice Cream Parlor Cocina Cucamonga Mexican Jolly Holiday Bakery Cafe Grill Cozy Cone Motel Little Red Wagon Cappuccino Cart Market House Fiddler, Fifer, & Practical Cafe Milk Stand Flo’s V8 Cafe Mint Julep Bar Ghirardelli Chocolate Factory Plaza Inn (modified) Hollywood Lounge Red Rose Tavern Lamplight Lounge River Belle Terrace Pacific Wharf Ronto Roasters Poultry Palace Ship to Shore Marketplace Rita’s Bajas Blenders Stage Door Cafe Senor Buzz Churros Tropical Hideaway Smokejumper’s Grill Churros, popcorn, & ice Sonoma Terrace cream carts Studio Catering Co. ALLACCESSDISNEYLAND.COM AVAILABLE ATTRACTIONS WHEN PARKS REOPEN Games of Pixar Pier Pixar Pal-A-Round Goofy’s Sky School Radiator Springs Racers Guardians of the Galaxy Silly Symphony Swings Incredicoaster Soarin’ Around the World Inside Out Emotional The Little Mermaid Whirlwind Toy Story Midway Mania Jessie’s Critter Carousel Turtle Talk with Crush Jumpin’ Jellyfish Mickey’s Philharmonic Luigi’s Rollickin’ Roadsters Monsters Inc. Mater’s Junkyard Jamboree ALLACCESSDISNEYLAND.COM ALLACCESSDISNEYLAND.COM AVAILABLE ATTRACTIONS WHEN PARKS REOPEN Alice in Wonderland Indiana Jones Adventure Astro Orbitor It’s a Small World Autopia King Arthur Carrousel Big Thunder Mountain Mad Tea Party Railroad Mark Twain Riverboat Casey Jr. Circus Train Main Street Vehicles Disneyland Railroad -

EXTRA TICKET AVAILABLE for PURCHASE 2019 NATIONAL DANCE TEAM CHAMPIONSHIP *ONLY Available Online at Uda.Varsity.Com
EXTRA TICKET AVAILABLE FOR PURCHASE 2019 NATIONAL DANCE TEAM CHAMPIONSHIP *ONLY AVAILABLE ONLINE AT UDA.VARSITY.COM. EXTRA NOTE: TRANSPORTATION IS NOT INCLUDED WITH PURCHASE OF THESE TICKETS! Extra tickets may ONLY be ordered on uda.varsity.com under the NATIONAL DANCE TEAM CHAMPIONSHIP Tickets can be picked up in Orlando Wednesday, January 30 through Saturday, February 2, 2019. TICKET Instructions on where to pick these tickets up will be sent to you at a later date. WALT DISNEY WORLD® TICKETS AVAILABLE FOR PURCHASE ® THREE DAY PARK HOPPER - $335 each/ $350 if purchased in Orlando AVAILABLE FOR PURCHASE (Championship Transportation is not included) Includes Three Days admission to ESPN Wide World of Sports®. All Walt Disney World® Theme Park Tickets are valid January 30 - February 16, 2019. FOUR DAY PARK HOPPER® - $380 each/ $395 if purchased in Orlando (Championship Transportation is not included) Includes Three Days admission to ESPN Wide World of Sports®. All Walt Disney World® Theme Park Tickets are valid January 30 - February 16, 2019. FIVE DAY PARK HOPPER® - $425 each/ $440 if purchased in Orlando (Championship Transportation is not included) Includes Three Days admission to ESPN Wide World of Sports®. All Walt Disney World® Theme Park Tickets are valid January 30 - February 16, 2019. COUNTER SERVICE MEAL VOUCHERS - $17.00 each/ not sold in Orlando (One entreé and beverage per voucher - at designated Theme Park dining locations. Lunch or Dinner Only. Does not include dessert.) SUNDAY EVENING PRIVATE CELEBRATION PARTY AT MAGIC KINGDOM® PARK - $45 Includes a DJ at Rocket Tower Stage in Tomorrowland, Space Mountain, Astro Orbiter, Tomorrowland Speedway, Buzz Lightyear’s Space Ranger Spin, Seven Dwarf’s Mine Train and Mad Tea Party. -

Magic Kingdom® Park During Front of the Park
TIPS & INFORMATION English GUEST RELATIONS PARK RULES Please visit Guest Relations located To provide a comfortable, safe and GUIDEMAP inside City Hall for: enjoyable experience for our Guests, • Questions and Concerns please comply with Park rules, signs and • Ticket Upgrades instructions including: • Separated Guest Assistance • All bags are subject to inspection • Lost and Found prior to admission. To report a lost item, please visit • Proper attire is required. disneyworld.com/lostandfound. • Smoking is allowed only in • Services for Guests with designated areas. Disabilities • Weapons are strictly prohibited. • Guests may be asked to leave if Happily Ever After Merchandise Package Delivery and Pickup deemed appropriate. Presented by PANDORA® Jewelry Instead of carrying your purchases all day, have them delivered Services for International Guests are Come experience the grandest to the Main Street Chamber of Commerce near the Park entrance and pick Additional details and a complete listing available at Guest Relations. of finales to your day in them up as you exit the Park. Please allow three hours for delivery to the of Park rules are available at Guest Magic Kingdom® Park during front of the Park. If you prefer, have your purchases delivered directly to Los Servicios para Huéspedes Relations or disneyworld.com/parkrules. internacionales están disponibles en la Happily Ever After––the newest, your Disney Resort hotel. See a Merchandise Cast Member for oficina de Guest Relations. Liberty Square Ticket Office most spectacular fireworks show in more details. Visit for assistance with ticket upgrades, the Park’s history! See Times Guide. Des services pour les Visiteurs My Disney Experience and FastPass+ internationaux sont disponibles au DINING selections, dining and reservations. -

FEB 08 2017 E-Mail: [email protected] 4 4VID H, YAMASAKI, CI� Court
• ELECTRONICALLY RECEIVED Supplier Court of CaMania. Gouty of Orenp 012712011 A 05 10 48 PM Cie* of the Sorrier Deer BY &Mir Demity Clerk 1 WILLIAM VERICK (SBN 140972) FILED SUPERIOR COURT OF CALIFORNIA Klamath Environmental Law Center COUNTY OF ORANGE 2 1125 Sixteenth Street, Suite 204 CENTRAL JUSTICE CENTER Arcata, CA 95521 3 Telephone: (707) 630-5061 • FEB 08 2017 E-mail: [email protected] 4 4VID H, YAMASAKI, CI Court 5 DAVID H. WILLIAMS (SBN 144479) MOP UTY BRIAN ACREE (SBN 202505) 6 Public Interest Lawyers Group 1990 N. California Blvd., 8th Floor 7 Walnut Creek, CA 94596 Telephone: (510) 847-2356 8 E-mail: [email protected] [email protected] 9 Attorneys for Plaintiff 10 MATEEL ENVIRONMENTAL JUSTICE FOUNDATION 11 12 SUPERIOR COURT OF THE STATE OF CALIFORNIA 13 COUNTY OF ORANGE 14 MATEEL ENVIRONMENTAL JUSTICE Case No.: 30-2015-00810110-CU-BT-CJC 15 FOUNDATION, STIPULATED CONSENT 16 Plaintiff, JUDGMENT 17 v. Dept: C25 Judge: Hon. Sheila Fell 18 WALT DISNEY PARKS AND RESORTS U.S., INC., 19 Defendant. 20 21 22 23 24 25 26 27 28 37542714v1 [Dik€PeSED] STIPULATED CONSENT JUDGMENT Case No.: 30-2015-00810110 1. INTRODUCTION 1.1 The Parties to this Consent Judgment are Mateel Environmental Justice Foundation ("Mateel") and Defendant Walt Disney Parks and Resorts U.S., Inc. ("Disneyland"). Mateel and Disneyland are referred to collectively as the "Parties" and individually as a "Party." The Parties enter into this Stipulated Consent Judgment ("Consent Judgment") to settle certain claims asserted by Mateel, as set forth below. 1.2 Disneyland is a business with ten or more employees.